小学数学苏教版六年级上1.长方体和正方体 整理与练习课件(共28张PPT)
文档属性
| 名称 | 小学数学苏教版六年级上1.长方体和正方体 整理与练习课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 21:42:43 | ||
图片预览






文档简介
(共28张PPT)
10 整理与练习
第1单元 长方体和正方体
学习目标
2.通过练习巩固本单元的基础知识,形成知识体系。进一步培养空间观念。
1. 以小组讨论的方式,对本单元所学内容进行梳理,进一步完善有关长方体和正方体的认知结构。
长方体有6个面,12条棱,8个顶点,相对的棱长度相等,相对的面完全相同。
正方体有6个面,12条棱,8个顶点;它的棱长度相等,每个面完全相同。
正方体是特殊的长方体。
回顾与整理
1.正方体和长方体各有哪些特征?什么联系?
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3) 。
回顾与整理
2.体积和容积的意义分别是什么?常用的体积单位有哪些?
计算长方体、正方体的表面积就是算出长方体、正方体6个面的总面积。
解决有关实际问题时要注意根据实际问题的特点,灵活运用长方体、正方体表面积的计算方法解决问题。
回顾与整理
3.怎样计算长方体、正方体的表面积?解决有关实际问题时要注意什么?
长方体所含体积单位的数量正好等于长、宽、高的乘积。
应用公式能解决包装盒的体积等实际问题。
回顾与整理
4.你是怎样发现长方体(或正方体)体积公式的?应用这些公式能解决哪些实际问题?
练习与应用
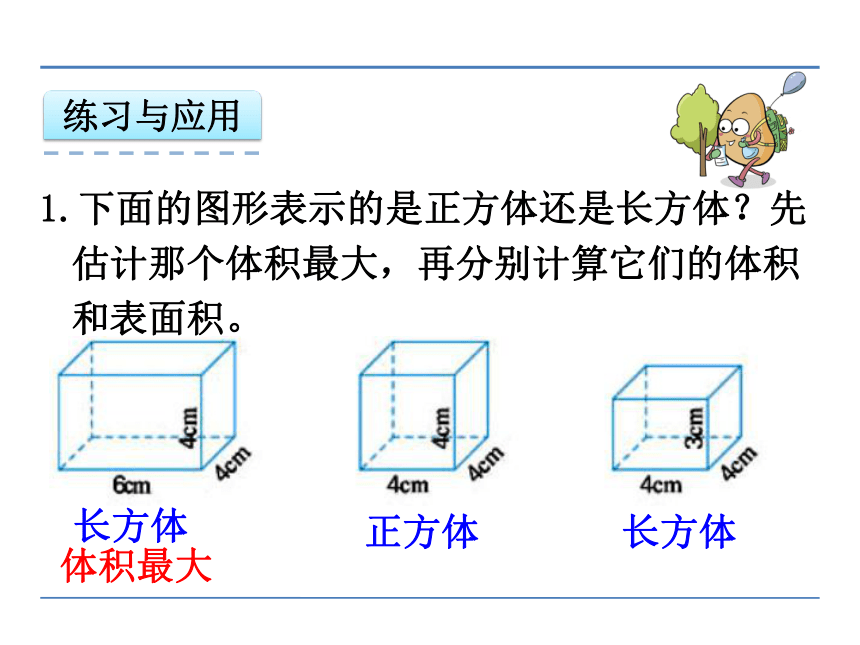
长方体
正方体
长方体
体积最大
1.下面的图形表示的是正方体还是长方体?先估计那个体积最大,再分别计算它们的体积和表面积。
练习与应用
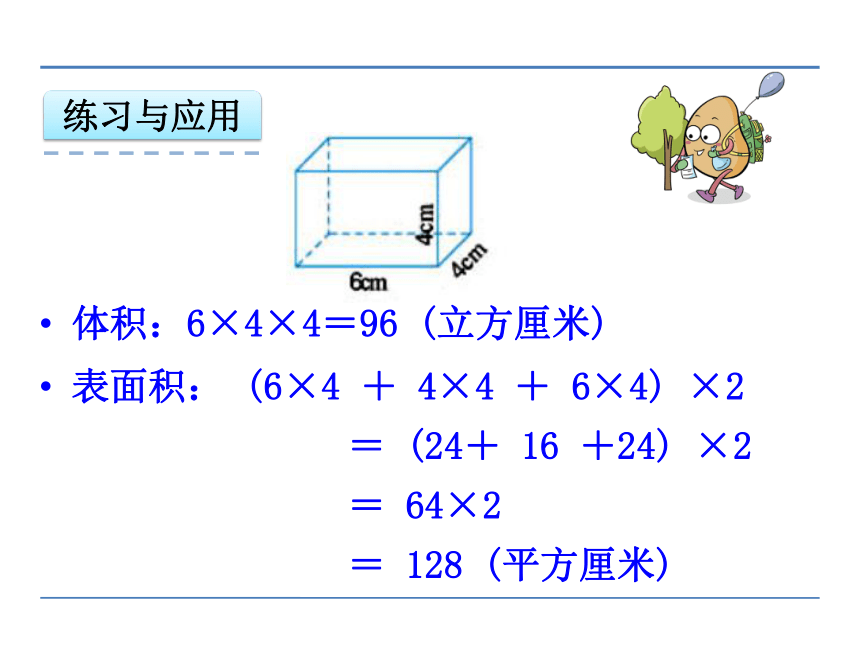
体积:6×4×4=96 (立方厘米)
表面积: (6×4 + 4×4 + 6×4) ×2
= (24+ 16 +24) ×2
= 64×2
= 128 (平方厘米)
练习与应用
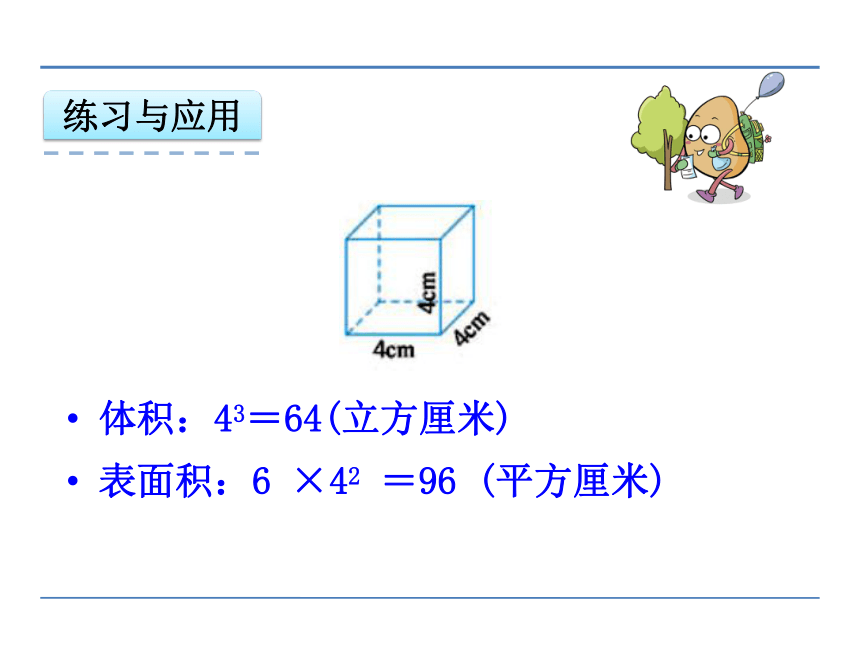
体积:43=64(立方厘米)
表面积:6 ×42 =96 (平方厘米)
练习与应用
体积:4×4×3=48 (立方厘米)
表面积: (4×3+ 4×3 + 4×4) ×2
= (12+ 12 +16) ×2
= 40×2
= 80 (平方厘米)
练习与应用
2.一个土豆浸没在盛有水的量杯中,这个土豆的体积是多少立方厘米?
800- 600 =200(毫升)
200毫升=200 立方厘米
答:这个土豆的体积是200立方厘米。
练习与应用
7.02dm3 =( )cm3 3.2m3=( )dm3
8020dm3=( )m3 4200cm3=( )dm3
4.5L=( )mL=( )cm3 2300mL=( )L
7020
3200
8.02
4.2
4500
4500
2.3
练习与应用
长/cm 宽/cm 高/cm 底面积/cm2 表面积/cm2 体积/cm3
长方体 12 9 5
3.2 6.4 25.6
正方体 8
4.
108
426
540
2
4
54.4
64
384
512
练习与应用
5.右边的长方体和正方体都是用棱长1厘米的正方体摆成的。它们的表面积和体积各是多少?
(4×2+ 3×2 + 4×3) ×2
= (8+6+12) ×2
= 26×2
=52(平方厘米)
4×2×3=24 (立方厘米)
答:长方体的表面积是52平方厘米,体积是24立方厘米。
22×6 =24(平方厘米)
23=8 (立方厘米)
答:正方体的表面积是24平方厘米,体积是8立方厘米。
练习与应用
6.下面是长方体和正方体的表面展开图,你能先测量,再分别算出它们的表面积和体积吗?
表面积: (2×1+ 1.5×1 + 2×1.5) ×2
= 6.5×2
= 13 (平方厘米)
体积:2×1×1.5=3 (立方厘米)
表面积: 0.92×6= 4.86 (平方厘米)
体积:0.93=0.729 (立方厘米)
练习与应用
7.有一个花坛,高0.5米,底面是边长1.3米的正方形。四周用砖砌成,砖墙的厚度是0.3米,中间填满泥土。
(1)花坛所占的空间有多大?
1.3×1.3×0.5=0.845(立方米)
答:花坛所占的空间是0.845立方米。
(2)花坛里大约有泥土多少立方米?
1.3-0.3×0.2=0.7(米)
0.7×0.7×0.5=0.245(立方米)
答:花坛里大约有泥土0.245立方米。
练习与应用
8.一种长方体的广告灯箱,框架由铝合金条制成,各个面都用灯箱布围成。制作一个这样的广告灯箱,至少需要铝合金条多少分米?需要灯箱布多少平方分米?
120×2+ 70×4 + 15×4
= 480+ 280+ 60
=820(厘米)
820厘米=82分米
答:至少需要铝合金条82分米。
(70×120+ 15×120 + 70×15) ×2
= (8400+1800+1050) ×2
= 11250×2
=22500(平方厘米)
22500平方厘米=225平方分米
答:需要灯箱布225平方分米。
练习与应用
9.一种正方体的工艺蜡烛盒,四周和底面都是玻璃,棱长6厘米。这个蜡烛盒的体积是多少立方厘米?做这个蜡烛盒至少要用多少玻璃?
63=216(立方厘米)
6 ×6 ×5
=36 ×5
=180(平方厘米)
答:这个蜡烛盒的体积是216立方厘米,
做这个蜡烛盒至少要用180平方厘米玻璃。
练习与应用
10.一件雕塑的底座是用混凝土浇筑成的棱长2.6米的正方体。
(1)这件雕塑的底座占地多少平方米?
2.6 ×2.6=6.76(平方米)
答:这件雕塑的底座占地6.76平方米。
(2)浇筑这件雕塑的底座需要混凝土多少立方米?
2.63=17.576(立方米)
答:浇筑这件雕塑的底座需要混凝土17.576立方米。
练习与应用
10.一件雕塑的底座是用混凝土浇筑成的棱长2.6米的正方体。
(3)给底座四面贴上花岗石,贴花岗石的面积是多少平方米?
2.6× 2.6 × 4=27.04(平方米)
答:贴花岗石的面积是27.04平方米。
探索与实践
11.用小棒和橡皮泥团,可以做出不同的长方体和正方体框架。小组合作,先填写选料单,再做一做。
探索与实践
12.调查几种长方体形状家用电器长、宽、高的数据,算出它们的表面积和体积。
探索与实践
13.你能求出一张纸的体积吗?小组合作,动手试一试。
思考题
右图中一共有多少个小正方体?你是怎样数的?与同学交流。
43 =64(个)
64-9 -4 -1=50(个)
答:右图中一共有50个小正方体。
易错提醒
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(118平方分米)。
错误解答
错解分析:解决有关长方体表面积的实际问题时,不能机械地套用长方体的表面积计算方法,要弄清楚要求的是哪几个面的面积。
易错提醒
错误解答
正确解答
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(118平方分米)。
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(94平方分米)。
一块长方体木料长4米,沿横截面切成两段,表面积增加了2.4平方米,这块木料的体积是多少?
2.4 ×4=9.6(平方米)
答:这块木料的体积是9.6平方米。
易错提醒
错解分析:要弄清立体图形分与合后,表面积增加或减少了几个面的面积。
错误解答
易错提醒
错误解答
2.4 ÷2×4=4.8(平方米)
答:这块木料的体积是4.8平方米。
正确解答
一块长方体木料长4米,沿横截面切成两段,表面积增加了2.4平方米,这块木料的体积是多少?
2.4 ×4=9.6(平方米)
答:这块木料的体积是9.6平方米。
10 整理与练习
第1单元 长方体和正方体
学习目标
2.通过练习巩固本单元的基础知识,形成知识体系。进一步培养空间观念。
1. 以小组讨论的方式,对本单元所学内容进行梳理,进一步完善有关长方体和正方体的认知结构。
长方体有6个面,12条棱,8个顶点,相对的棱长度相等,相对的面完全相同。
正方体有6个面,12条棱,8个顶点;它的棱长度相等,每个面完全相同。
正方体是特殊的长方体。
回顾与整理
1.正方体和长方体各有哪些特征?什么联系?
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3) 。
回顾与整理
2.体积和容积的意义分别是什么?常用的体积单位有哪些?
计算长方体、正方体的表面积就是算出长方体、正方体6个面的总面积。
解决有关实际问题时要注意根据实际问题的特点,灵活运用长方体、正方体表面积的计算方法解决问题。
回顾与整理
3.怎样计算长方体、正方体的表面积?解决有关实际问题时要注意什么?
长方体所含体积单位的数量正好等于长、宽、高的乘积。
应用公式能解决包装盒的体积等实际问题。
回顾与整理
4.你是怎样发现长方体(或正方体)体积公式的?应用这些公式能解决哪些实际问题?
练习与应用
长方体
正方体
长方体
体积最大
1.下面的图形表示的是正方体还是长方体?先估计那个体积最大,再分别计算它们的体积和表面积。
练习与应用
体积:6×4×4=96 (立方厘米)
表面积: (6×4 + 4×4 + 6×4) ×2
= (24+ 16 +24) ×2
= 64×2
= 128 (平方厘米)
练习与应用
体积:43=64(立方厘米)
表面积:6 ×42 =96 (平方厘米)
练习与应用
体积:4×4×3=48 (立方厘米)
表面积: (4×3+ 4×3 + 4×4) ×2
= (12+ 12 +16) ×2
= 40×2
= 80 (平方厘米)
练习与应用
2.一个土豆浸没在盛有水的量杯中,这个土豆的体积是多少立方厘米?
800- 600 =200(毫升)
200毫升=200 立方厘米
答:这个土豆的体积是200立方厘米。
练习与应用
7.02dm3 =( )cm3 3.2m3=( )dm3
8020dm3=( )m3 4200cm3=( )dm3
4.5L=( )mL=( )cm3 2300mL=( )L
7020
3200
8.02
4.2
4500
4500
2.3
练习与应用
长/cm 宽/cm 高/cm 底面积/cm2 表面积/cm2 体积/cm3
长方体 12 9 5
3.2 6.4 25.6
正方体 8
4.
108
426
540
2
4
54.4
64
384
512
练习与应用
5.右边的长方体和正方体都是用棱长1厘米的正方体摆成的。它们的表面积和体积各是多少?
(4×2+ 3×2 + 4×3) ×2
= (8+6+12) ×2
= 26×2
=52(平方厘米)
4×2×3=24 (立方厘米)
答:长方体的表面积是52平方厘米,体积是24立方厘米。
22×6 =24(平方厘米)
23=8 (立方厘米)
答:正方体的表面积是24平方厘米,体积是8立方厘米。
练习与应用
6.下面是长方体和正方体的表面展开图,你能先测量,再分别算出它们的表面积和体积吗?
表面积: (2×1+ 1.5×1 + 2×1.5) ×2
= 6.5×2
= 13 (平方厘米)
体积:2×1×1.5=3 (立方厘米)
表面积: 0.92×6= 4.86 (平方厘米)
体积:0.93=0.729 (立方厘米)
练习与应用
7.有一个花坛,高0.5米,底面是边长1.3米的正方形。四周用砖砌成,砖墙的厚度是0.3米,中间填满泥土。
(1)花坛所占的空间有多大?
1.3×1.3×0.5=0.845(立方米)
答:花坛所占的空间是0.845立方米。
(2)花坛里大约有泥土多少立方米?
1.3-0.3×0.2=0.7(米)
0.7×0.7×0.5=0.245(立方米)
答:花坛里大约有泥土0.245立方米。
练习与应用
8.一种长方体的广告灯箱,框架由铝合金条制成,各个面都用灯箱布围成。制作一个这样的广告灯箱,至少需要铝合金条多少分米?需要灯箱布多少平方分米?
120×2+ 70×4 + 15×4
= 480+ 280+ 60
=820(厘米)
820厘米=82分米
答:至少需要铝合金条82分米。
(70×120+ 15×120 + 70×15) ×2
= (8400+1800+1050) ×2
= 11250×2
=22500(平方厘米)
22500平方厘米=225平方分米
答:需要灯箱布225平方分米。
练习与应用
9.一种正方体的工艺蜡烛盒,四周和底面都是玻璃,棱长6厘米。这个蜡烛盒的体积是多少立方厘米?做这个蜡烛盒至少要用多少玻璃?
63=216(立方厘米)
6 ×6 ×5
=36 ×5
=180(平方厘米)
答:这个蜡烛盒的体积是216立方厘米,
做这个蜡烛盒至少要用180平方厘米玻璃。
练习与应用
10.一件雕塑的底座是用混凝土浇筑成的棱长2.6米的正方体。
(1)这件雕塑的底座占地多少平方米?
2.6 ×2.6=6.76(平方米)
答:这件雕塑的底座占地6.76平方米。
(2)浇筑这件雕塑的底座需要混凝土多少立方米?
2.63=17.576(立方米)
答:浇筑这件雕塑的底座需要混凝土17.576立方米。
练习与应用
10.一件雕塑的底座是用混凝土浇筑成的棱长2.6米的正方体。
(3)给底座四面贴上花岗石,贴花岗石的面积是多少平方米?
2.6× 2.6 × 4=27.04(平方米)
答:贴花岗石的面积是27.04平方米。
探索与实践
11.用小棒和橡皮泥团,可以做出不同的长方体和正方体框架。小组合作,先填写选料单,再做一做。
探索与实践
12.调查几种长方体形状家用电器长、宽、高的数据,算出它们的表面积和体积。
探索与实践
13.你能求出一张纸的体积吗?小组合作,动手试一试。
思考题
右图中一共有多少个小正方体?你是怎样数的?与同学交流。
43 =64(个)
64-9 -4 -1=50(个)
答:右图中一共有50个小正方体。
易错提醒
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(118平方分米)。
错误解答
错解分析:解决有关长方体表面积的实际问题时,不能机械地套用长方体的表面积计算方法,要弄清楚要求的是哪几个面的面积。
易错提醒
错误解答
正确解答
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(118平方分米)。
一个长方体无盖包装盒,长为6分米,宽为4分米,高为3.5分米,其表面积为(94平方分米)。
一块长方体木料长4米,沿横截面切成两段,表面积增加了2.4平方米,这块木料的体积是多少?
2.4 ×4=9.6(平方米)
答:这块木料的体积是9.6平方米。
易错提醒
错解分析:要弄清立体图形分与合后,表面积增加或减少了几个面的面积。
错误解答
易错提醒
错误解答
2.4 ÷2×4=4.8(平方米)
答:这块木料的体积是4.8平方米。
正确解答
一块长方体木料长4米,沿横截面切成两段,表面积增加了2.4平方米,这块木料的体积是多少?
2.4 ×4=9.6(平方米)
答:这块木料的体积是9.6平方米。
