专题8 几何初步、平行线、三角形(含解析)-2025年浙江省中考数学一模试题精编
文档属性
| 名称 | 专题8 几何初步、平行线、三角形(含解析)-2025年浙江省中考数学一模试题精编 |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 17:17:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题8 几何初步、平行线、三角形
一.选择题
1.(2025 浙江一模)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
2.(2025 浙江一模)将一个含45°角的三角尺和直尺如图放置.若∠1=65°,则∠2=( )
A.20° B.25° C.30° D.35°
3.(2025 嘉兴模拟)在同一平面内,将直尺、直角三角尺(∠CAB=30°)和木工角尺(DE⊥DF)按如图方式摆放,若AC∥DE,则∠1的度数为( )
A.30° B.45° C.60° D.75°
4.(2025 浙江模拟)如图,张师傅将两根木条AB和AC固定在点A处,在木条AB上点O处安装一根能旋转的木条DE.张师傅用量角仪测得∠A=68°,木条DE与AB的夹角∠BOD=80°,要使DE∥AC,木条DE绕点O至少旋转( )
A.10° B.12° C.14° D.16°
5.(2025 西湖区一模)如图,一束光线PO从空气中斜射入长方体玻璃砖发生折射,已知AD∥BC,延长PO交BC于点P',若∠POA=50°,∠P'OQ=25°,则∠OQB的度数为( )
A.45° B.55° C.65° D.75°
6.(2025 衢江区一模)如图,已知两平行线a、b被直线c所截,∠1=37°,则∠2的度数为( )
A.153° B.143° C.63° D.53°
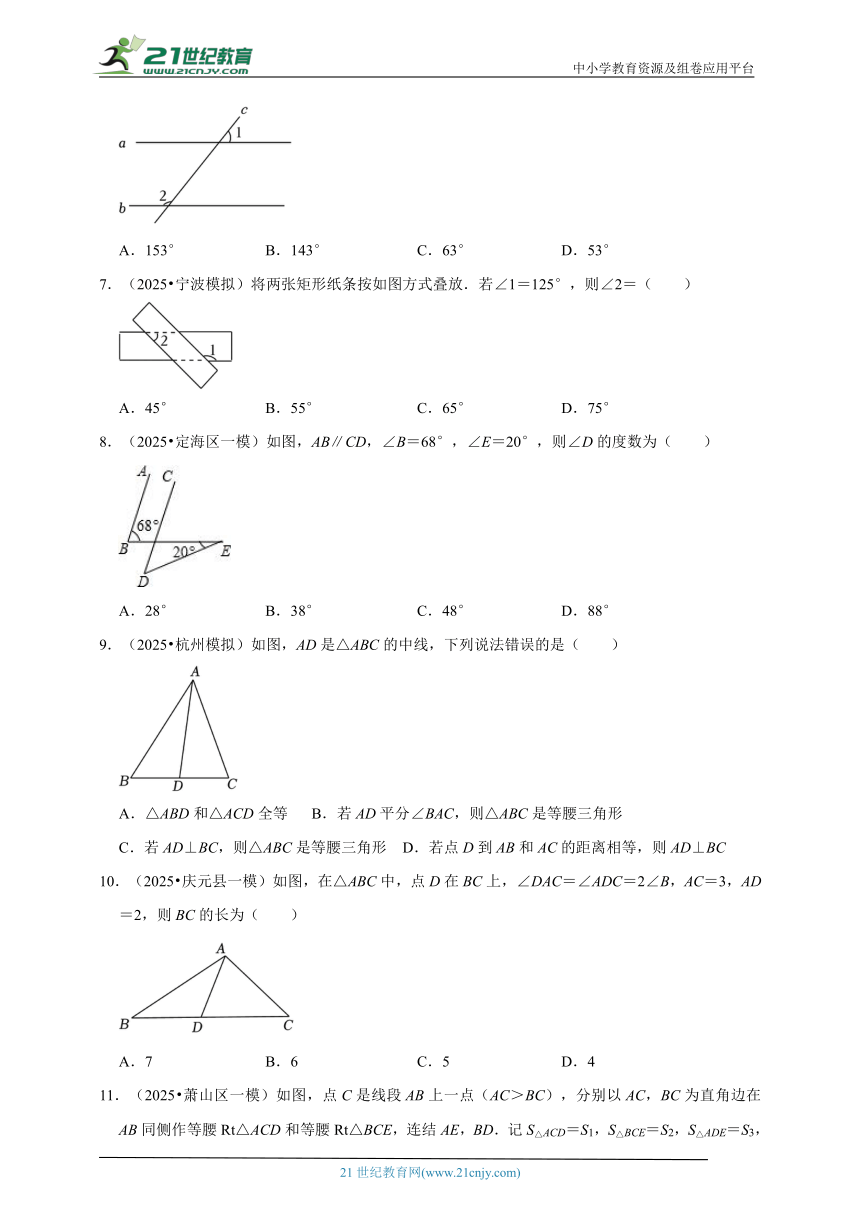
7.(2025 宁波模拟)将两张矩形纸条按如图方式叠放.若∠1=125°,则∠2=( )
A.45° B.55° C.65° D.75°
8.(2025 定海区一模)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
9.(2025 杭州模拟)如图,AD是△ABC的中线,下列说法错误的是( )
A.△ABD和△ACD全等 B.若AD平分∠BAC,则△ABC是等腰三角形
C.若AD⊥BC,则△ABC是等腰三角形 D.若点D到AB和AC的距离相等,则AD⊥BC
10.(2025 庆元县一模)如图,在△ABC中,点D在BC上,∠DAC=∠ADC=2∠B,AC=3,AD=2,则BC的长为( )
A.7 B.6 C.5 D.4
11.(2025 萧山区一模)如图,点C是线段AB上一点(AC>BC),分别以AC,BC为直角边在AB同侧作等腰Rt△ACD和等腰Rt△BCE,连结AE,BD.记S△ACD=S1,S△BCE=S2,S△ADE=S3,S△BDE=S4,若S1﹣S2=20,则S3+S4=( )
A.10 B.15 C.20 D.40
12.(2025 拱墅区一模)若△ABC是锐角三角形,且∠A=60°,则∠B可能的度数是( )
A.10° B.20° C.30° D.40°
13.(2025 宁波一模)如图,在△ABC中,AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,记BD长为x,CE长为y,x>y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B.x+y C.x﹣y D.x2+y2
14.(2025 绍兴一模)如图,Rt△ABC≌Rt△CDE,∠ABC=∠CDE=90°,C在线段BD上,F是AE的中点,连结BF,DF,若AB=1,DE=2,则BF的长是( )
A. B. C. D.
15.(2025 浙江一模)如图,在△ABC中,点D在BC边上,2∠B=∠DAC,CE⊥AD,若AE=DE=2,AC=6,则BC的长为( )
A.10 B. C.8 D.
16.(2025 衢州一模)如图,是人字形钢架屋顶示意图(部分),其中AB=AC=8,AE=BE,且∠B=30°,∠EFB=∠ADB=90°,则DF的长为( )
A. B. C. D.1
二.填空题
17.(2025 湖州一模)把角度转化成度的形式:70°30′= °.
18.(2025 金华模拟)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,则∠ABC的度数为 °.
19.(2025 萧山区一模)如图,AD∥BC,AC平分∠BAD,若∠ABC=110°,则∠CAD= .
20.(2025 浙江模拟)如图,∠B=20°,∠C=31°,∠BPC=123°,则∠A= °.
21.(2025 上城区一模)如图,在△ABC中,BC=4,BD是AC边上的中线,D点到BC的距离为2,则S△ABC= .
22.(2025 浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
23.(2025 拱墅区一模)如图,在△ABC中,∠C=90°,BD是∠ABC的角平分线,点E在BD上,过点E作EF⊥BD,交AB于点F.若BE=4,BF=5,DE=EF,则BC= .
24.(2025 浙江一模)如图,在△ABC中,AD是BC上的中线,BE⊥AC交AD于点F,AF=DF.若,EC=2,则AB的长为 .
25.(2025 杭州一模)等腰三角形的顶角为100°,则它的一个底角度数为 .
三.解答题
26.(2025 拱墅区一模)如图,在△ABC中,AB=AC,BD,BE分别是边AC上的高线和中线.
(1)若∠A=40°,求∠CBD的度数.
(2)求证:AD﹣CD=2DE.
27.(2025 台州一模)如图,在△ABC中,AB=AC,点O为BC中点,点D在边AB上,连接OD.
(1)如图1,若OD⊥AB,OE⊥AC于点E,求证:OE=OD;
(2)如图2,已知∠BAC=90°,AB=4,AD=1.若点F在边AC上,OF=OD,求AF的长.
28.(2025 宁波模拟)如图,在△ABC中,CE⊥AB于点E,点D在BC上,连结AD交CE于点F,BC=13,CE=12.
(1)求BE的长;
(2)若∠AFE=45°,AB=CF,求AE的长.
29.(2025 宁波一模)在△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F.
(1)若△ABC是正三角形,AD=CE,求sin∠BFE的值.
(2)设四边形CEFD的面积为S1,△AFD,△ABF,△BEF的面积分别为S2,S3,S4,求证:S1 S3>S2 S4.
答案与解析
一.选择题
1.(2025 浙江一模)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
【点拨】利用题中“一个角的余角是这个角的2倍”作为相等关系列方程求解即可.
【解析】解:设这个角是x,
则90°﹣x=2x,
解得x=30°.
故选:A.
【点睛】主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180度.解此题的关键是能准确的从图中找出角之间的数量关系,从而计算出结果.
2.(2025 浙江一模)将一个含45°角的三角尺和直尺如图放置.若∠1=65°,则∠2=( )
A.20° B.25° C.30° D.35°
【点拨】根据直尺两边平行,求出∠3的度数,再根据平角的性质,求解即可.
【解析】解:∵直尺对边平行,
∴∠3=∠1=65°,
∴∠2=25°.
故选:B.
【点睛】本题考查平行线的性质.熟练掌握平行线的性质是关键.
3.(2025 嘉兴模拟)在同一平面内,将直尺、直角三角尺(∠CAB=30°)和木工角尺(DE⊥DF)按如图方式摆放,若AC∥DE,则∠1的度数为( )
A.30° B.45° C.60° D.75°
【点拨】先根据AC∥DE求出∠BDE的度数,再结合DE⊥DF即可解决问题.
【解析】解:∵AC∥DE,∠CAB=30°,
∴∠BDE=∠CAB=30°.
又∵DE⊥DF,
∴∠EDF=90°,
∴∠1=180°﹣90°﹣30°=60°.
故选:C.
【点睛】本题主要考查了平行线的性质及垂线,熟知平行线的性质是解题的关键.
4.(2025 浙江模拟)如图,张师傅将两根木条AB和AC固定在点A处,在木条AB上点O处安装一根能旋转的木条DE.张师傅用量角仪测得∠A=68°,木条DE与AB的夹角∠BOD=80°,要使DE∥AC,木条DE绕点O至少旋转( )
A.10° B.12° C.14° D.16°
【点拨】由同位角相等,两直线平行,即可解决问题.
【解析】解:当∠BOD=∠A=68°时,DE∥AC,
∴木条DE绕点O至少逆时针旋转80°﹣68°=12°.
故选:B.
【点睛】本题考查平行线的判定,关键是掌握同位角相等,两直线平行.
5.(2025 西湖区一模)如图,一束光线PO从空气中斜射入长方体玻璃砖发生折射,已知AD∥BC,延长PO交BC于点P',若∠POA=50°,∠P'OQ=25°,则∠OQB的度数为( )
A.45° B.55° C.65° D.75°
【点拨】根据对顶角相等,角的和差关系计算∠DOQ的度数,再应用平行线的性质得到∠OQB的度数即可.
【解析】解:∵∠POA=∠DOP′,
∠POA=50°,
∴∠DOP′=50°,
∵∠DOQ=∠DOP'+∠P'OQ,
∠P′OQ=25°,
∴∠DOQ=50°+25°=75°,
∵AD∥BC,
∴∠OQB=∠DOQ=75°,
∴∠OQB的度数为75°.
故选:D.
【点睛】本题考查了平行线的性质,对顶角、邻补角,熟练掌握相关性质是解题的关键.
6.(2025 衢江区一模)如图,已知两平行线a、b被直线c所截,∠1=37°,则∠2的度数为( )
A.153° B.143° C.63° D.53°
【点拨】由平行线的性质推出∠3=∠1=37°,由邻补角的性质即可求出∠2的度数,
【解析】解:∵a∥b,
∴∠3=∠1=37°,
∴∠2=180°﹣∠3=143°.
故选:B.
【点睛】本题考查平行线的性质,关键是由平行线的性质推出∠3=∠1.
7.(2025 宁波模拟)将两张矩形纸条按如图方式叠放.若∠1=125°,则∠2=( )
A.45° B.55° C.65° D.75°
【点拨】先根据矩形的性质得到AB∥CD,AC∥BD,再根据平行线的性质得到∠3=∠1=125°,∠2+∠3=180°,进而可求解.
【解析】解:如图,
由平行线可知∠3=∠1=125°,∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣125°=55°,
故选:B.
【点睛】本题考查矩形的性质、平行线的性质,熟练掌握平行线的性质是解答的关键.
8.(2025 定海区一模)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
【点拨】根据平行线的性质得到∠1=∠B=68°,由三角形的外角的性质即可得到结论.
【解析】解:如图,∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°,
故选:C.
【点睛】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键.
9.(2025 杭州模拟)如图,AD是△ABC的中线,下列说法错误的是( )
A.△ABD和△ACD全等 B.若AD平分∠BAC,则△ABC是等腰三角形
C.若AD⊥BC,则△ABC是等腰三角形 D.若点D到AB和AC的距离相等,则AD⊥BC
【点拨】根据中线的定义、全等三角形的判定判断A;延长AD至E,使DE=AD,连接CE,证明△ADB≌△EDC,根据全等三角形的性质判断B;根据线段垂直平分线的性质判断C;根据B选项结论判断D.
【解析】解:A、∵AD是△ABC的中线,
∴BD=DC,
但AB与AC的关系不能确定,
∴△ABD和△ACD不一定全等,本选项说法错误,符合题意;
B、如图,延长AD至E,使DE=AD,连接CE,
则△ADB≌△EDC(SAS),
∴AB=CE,∠BAD=∠E,
∴AC=CE,
∴AB=AC,
∴△ABC是等腰三角形,本选项说法正确,不符合题意;
C、∵AD⊥BC,BD=DC,
∴AD是BC的垂直平分线,
∴AB=AC,
∴△ABC是等腰三角形,本选项说法正确,不符合题意;
D、∵点D到AB和AC的距离相等,
∴AD平分∠BAC,
由B选项可知:AB=AC,
∴AD⊥BC,本选项说法正确,不符合题意;
故选:A.
【点睛】本题考查的是三角形的角平分线、中线和高,掌握三角形的中线的定义、全等三角形的判定和性质是解题的关键.
10.(2025 庆元县一模)如图,在△ABC中,点D在BC上,∠DAC=∠ADC=2∠B,AC=3,AD=2,则BC的长为( )
A.7 B.6 C.5 D.4
【点拨】根据∠DAC=∠ADC得DC=AC=3,再根据三角形外角性质及已知条件证明∠B=∠DAB,则BD=AD=2,由此可得出BC的长.
【解析】解:∵∠DAC=∠ADC,AC=3,
∴DC=AC=3,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠DAB,
又∵∠ADC=2∠B,
∴2∠B=∠B+∠DAB,
∴∠B=∠DAB,
∴BD=AD=2,
∴BC=BD+CD=2+3=5.
故选:C.
【点睛】此题主要考查了等腰三角形的判定和性质,熟练掌握等腰三角形的判定和性质是解决问题的关键.
11.(2025 萧山区一模)如图,点C是线段AB上一点(AC>BC),分别以AC,BC为直角边在AB同侧作等腰Rt△ACD和等腰Rt△BCE,连结AE,BD.记S△ACD=S1,S△BCE=S2,S△ADE=S3,S△BDE=S4,若S1﹣S2=20,则S3+S4=( )
A.10 B.15 C.20 D.40
【点拨】依题意设AC=CD=a,BC=CE=b,则DE=CD﹣CE=a﹣b,进而得S1=a2,S2=b2,S3=(a2﹣ab),S4=(ab﹣b2),根据S1﹣S2=20得(a2﹣b2)=20,则S3+S4=(a2﹣b2)=20,据此即可得出答案.
【解析】解:依题意得:△ACD和△BCE都是直角三角形,∠ACD=∠BCE=90°,
∴设AC=CD=a,BC=CE=b,
∴DE=CD﹣CE=a﹣b,
∴S1=a2,S2=b2,S3=a(a﹣b)=(a2﹣ab),S4=b(a﹣b)=(ab﹣b2),
∵S1﹣S2=20,
∴a2﹣b2=20,
∴(a2﹣b2)=20,
∴S3+S4=(a2﹣ab+ab﹣b2)=(a2﹣b2)=20.
故选:C.
【点睛】此题主要考查了等腰直角三角形的性质,三角形的面积,准确试题,熟练掌握等腰直角三角形的性质,三角形的面积公式是解决问题的关键.
12.(2025 拱墅区一模)若△ABC是锐角三角形,且∠A=60°,则∠B可能的度数是( )
A.10° B.20° C.30° D.40°
【点拨】设∠B=x°(x>0),利用三角形内角和定理,可得出∠C=180°﹣60°﹣x°,结合△ABC是锐角三角形,可列出关于x的一元一次不等式组,解之可得出x的取值范围,进而可得出∠B度数的范围,再对照四个选项,即可得出结论.
【解析】解:设∠B=x°(x>0),则∠C=180°﹣60°﹣x°,
根据题意得:,
解得:30<x<90,
∴30°<∠B<90°.
故选:D.
【点睛】本题考查了三角形内角和定理、一元一次不等式组的应用以及三角形,根据各角度数之间的关系,正确列出关于x的一元一次不等式组是解题的关键.
13.(2025 宁波一模)如图,在△ABC中,AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,记BD长为x,CE长为y,x>y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B.x+y C.x﹣y D.x2+y2
【点拨】在CA上截取CF=BD=x,过B作BH⊥AC于H,则EF=x﹣y,证明△FCB和△DBC全等得BF=CD=BE=9,则EH=FH=EF=,由勾股定理得BH2=BF2﹣FH2=BC2﹣CH2,则=,整理得xy=19,由此即可得出答案.
【解析】在CA上截取CF=BD,过点B作BH⊥AC于点H,如图所示:
∵BD长为x,CE长为y,
∴CF=BD=x,
∴EF=CF﹣CE=x﹣y,
∵AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,
∴∠ACB=∠ABC,
在△FCB和△DBC中,,
∴△FCB≌△DBC(SAS),
∴BF=CD=BE=9,
∵BH⊥AC,
∴EH=FH=EF=,
在Rt△BHF和Rt△BHC中,由勾股定理得:BH2=BF2﹣FH2=BC2﹣CH2,
∴=,
整理得:xy=19,
∴当x,y的值发生变化时,代数式xy的值不变,始终等于19.
故选:A.
【点睛】此题主要考查了等腰三角形的性质,解直角三角形,勾股定理,熟练掌握等腰三角形的性质,灵活运用锐角三角函数的定义,勾股定理列代数式是解决问题的关键.
14.(2025 绍兴一模)如图,Rt△ABC≌Rt△CDE,∠ABC=∠CDE=90°,C在线段BD上,F是AE的中点,连结BF,DF,若AB=1,DE=2,则BF的长是( )
A. B. C. D.
【点拨】过点F作FH⊥BD于点H,根据全等三角形的性质得BC=DE=2,AB=CD=1,则BD=3,证明FH是直角梯形ABDE的中位线得FH=(AB+DE)=,BH=DH=BD=,然后在Rt△BHF中,由勾股定理即可求出BF的长.
【解析】解:过点F作FH⊥BD于点H,如图所示:
∵Rt△ABC≌Rt△CDE,AB=1,DE=2,
∴BC=DE=2,AB=CD=1,
∴BD=BC+CD=3,
∵∠ABC=∠CDE=90°,
∴AB⊥BD,DE⊥BD,
∴AB∥DE,
∴四边形ABDE是直角梯形,
∵FH⊥BD,
∴FH∥AB∥DE,
又∵F是AE的中点,
∴FH是直角梯形ABDE的中位线,
∴FH=(AB+DE)=,BH=DH=BD=,
在Rt△BHF中,由勾股定理得:BF===.
故选:D.
【点睛】此题主要考查了全等三角形的性质,勾股定理,熟练掌握全等三角形的性质,梯形的中位线定理,勾股定理是解决问题的关键.
15.(2025 浙江一模)如图,在△ABC中,点D在BC边上,2∠B=∠DAC,CE⊥AD,若AE=DE=2,AC=6,则BC的长为( )
A.10 B. C.8 D.
【点拨】根据线段的垂直平分线的性质得到CD=AC,根据等腰三角形的性质得到∠CDA=∠DAC,根据三角形的外角性质求出∠B=∠DAB,得到DB=DA=4,计算即可.
【解析】解:∵AE=DE=2,CE⊥AD,
∴AD=4,CE是AD的垂直平分线,
∴CD=AC=6,
∴∠CDA=∠DAC,
∵2∠B=∠DAC,
∴2∠B=∠CDA,
∵∠CDA=∠B+∠DAB,
∴∠B=∠DAB,
∴DB=DA=4,
∴BC=DB+DC=4+6=10,
故选:A.
【点睛】本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.
16.(2025 衢州一模)如图,是人字形钢架屋顶示意图(部分),其中AB=AC=8,AE=BE,且∠B=30°,∠EFB=∠ADB=90°,则DF的长为( )
A. B. C. D.1
【点拨】先在Rt△ABD中,利用直角三角形斜边上的中线性质可得DE=AE=BE=4,然后利用含30度角的直角三角形的性质可得AD=4,BD=4,再利用等腰三角形的三线合一性质进行计算即可解答.
【解析】解:∵∠ADB=90°,AE=BE,
∴DE=AE=BE=AB=4,
∵∠B=30°,
∴AD=AB=4,BD=AD=4,
∵∠EFB=90°,
∴BF=DF=BD=2,
故选:B.
【点睛】本题考查了等腰三角形的性质,直角三角形斜边上的中线,含30度角的直角三角形,根据题目的已知条件并结合图形进行分析是解题的关键.
二.填空题
17.(2025 湖州一模)把角度转化成度的形式:70°30′= 70.5 °.
【点拨】根据度分秒的进制进行计算,即可解答.
【解析】解:∵30′=0.5°,∴70°30′=70.5°.
故答案为:70.5.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
18.(2025 金华模拟)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,则∠ABC的度数为 105 °.
【点拨】根据方向角求出∠EBC,再根据平行线的性质求出∠ABE即可得出答案.
【解析】解:如图:
∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,
∴∠DAB=40°,∠CBE=65°,
∵AD∥BE,
∴∠ABE=∠DAB=40°,
∴∠ABC=∠ABE+∠EBC=40°+65°=105°.
故答案为:105.
【点睛】本题考查了方向角,熟练掌握方向角的定义是解题的关键.
19.(2025 萧山区一模)如图,AD∥BC,AC平分∠BAD,若∠ABC=110°,则∠CAD= 35° .
【点拨】根据平行线的性质以及角平分线的定义求解即可.
【解析】解:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠B=110°,
∴∠BAD=180°﹣∠B=70°,
∵AC平分∠BAD,
∴∠CAD=∠BAD=35°,
故答案为:35°.
【点睛】本题考查了平行线的性质,根据题目的已知条件并结合图形进行分析是解题的关键.
20.(2025 浙江模拟)如图,∠B=20°,∠C=31°,∠BPC=123°,则∠A= 72 °.
【点拨】连接AP并延长至点D,利用∠BPD=∠BAP+∠B,∠CPD=∠CAP+∠C,得∠BPC=∠BPD+∠CPD=∠BAP+∠B+∠CAP+∠C=123°,即∠BAC+∠B+∠C=123°,代入∠B=20°,∠C=31°,即可求解.
【解析】解:如图,连接AP并延长至点D,
有由意可得:
∠BPC=∠BPD+∠CPD=∠BAP+∠B+∠CAP+∠C=123°,
∴∠BAC+∠B+∠C=123°,
∵∠B=20°,∠C=31°,
∴∠BAC=123°﹣∠B﹣∠C=72°,
故答案为:72.
【点睛】本题考查三角形的外角的性质,熟练掌握三角形的外角等于和它不相邻的两个内角的和是解题的关键.
21.(2025 上城区一模)如图,在△ABC中,BC=4,BD是AC边上的中线,D点到BC的距离为2,则S△ABC= 8 .
【点拨】首先利用已知条件求出△BDC的面积,然后利用中线的性质即可求出△ABC的面积.
【解析】解:∵在△ABC中,BC=4,D点到BC的距离为2,
∴S△BDC=×BC×2=×4×2=4,
而BD是AC边上的中线,
∴S△ABC=2S△BDC=2×4=8.
故答案为:8.
【点睛】此题主要考查了三角形面积的计算,解题的关键是熟练利用三角形的中线平分三角形面积这个性质解决问题.
22.(2025 浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 16 .
【点拨】根据勾股定理求出AB的长,再分别求出以AC为直径的半圆的面积与以BC为直径的半圆的面积以及以AB为直径的半圆的面积与△ABC的面积,即可求解.
【解析】解:在Rt△ABC中,∠C=90°,
∴AB==4,
以AC为直径的半圆的面积===8π,
以BC为直径的半圆的面积===2π,
以AB为直径的半圆的面积=,
S=16,
∴S阴影=8π+2π+16﹣10π=16,
故答案为:16.
【点睛】本题考查了勾股定理,半圆面积的计算,正确得出阴影部分面积的计算方法是解题的关键.
23.(2025 拱墅区一模)如图,在△ABC中,∠C=90°,BD是∠ABC的角平分线,点E在BD上,过点E作EF⊥BD,交AB于点F.若BE=4,BF=5,DE=EF,则BC= .
【点拨】作DH⊥AB于点H,则∠BHD=∠C=90°,而∠HBD=∠CBD,BD=BD,可根据“AAS”证明△HBD≌△CBD,由∠BEF=90°,BE=4,BF=5,求得DE=EF=3,则BD=7,由cos∠ABD===,求得BH=BD=,则BC=BH=,于是得到问题的答案.
【解析】解:作DH⊥AB于点H,则∠BHD=∠C=90°,
∵BD是∠ABC的角平分线,
∴∠HBD=∠CBD,
∵BD=BD,
∴△HBD≌△CBD(AAS),
∵EF⊥BD于点E,
∴∠BEF=90°,
∵BE=4,BF=5,
∴DE=EF===3,
∴BD=BE+DE=4+3=7,
∵cos∠ABD===,
∴BH=BD=×7=,
∴BC=BH=,
故答案为:.
【点睛】此题重点考查全等三角形的判定与性质、勾股定理、解直角三角形等知识,正确地添加辅助线是解题的关键.
24.(2025 浙江一模)如图,在△ABC中,AD是BC上的中线,BE⊥AC交AD于点F,AF=DF.若,EC=2,则AB的长为 .
【点拨】取EC中点M,连接MD,求出EM=1,判定DM是△BCD的中位线,推出EF∥DM,DM=BE,判定EF是△ADM的中位线,得到DM=2EF=,求出BE=2DM=3,由勾股定理求出AB=.
【解析】解:取EC中点M,连接MD,
∴EM=EC=×2=1,
∵AD是BC上的中线,
∴DM是△BCD的中位线,
∴EF∥DM,DM=BE,
∵AF=FD,
∴AE=EM=1,
∴EF是△ADM的中位线,
∴DM=2EF=2×=,
∴BE=2DM=3,
∵BE⊥AC交AD于点F,
∴AB==.
故答案为:.
【点睛】本题考查三角形中位线定理,勾股定理,关键是取CE中点M,构造三角形的中位线.
25.(2025 杭州一模)等腰三角形的顶角为100°,则它的一个底角度数为 40° .
【点拨】根据等腰三角形的性质和三角形内角和定理即可求解.
【解析】解:因为等腰三角形的顶角为100°,
所以这个等腰三角形的一个底角的度数为 (180°﹣100°)=40°.
故答案为:40°.
【点睛】本题考查了等腰三角形的性质和三角形的内角和定理,注意:三角形的三个内角的和等于180°,等边对等角.
三.解答题
26.(2025 拱墅区一模)如图,在△ABC中,AB=AC,BD,BE分别是边AC上的高线和中线.
(1)若∠A=40°,求∠CBD的度数.
(2)求证:AD﹣CD=2DE.
【点拨】(1)由AB=AC,得∠ABC=∠C,而∠A=40°,所以2∠C+40°=180°,求得∠C=70°,因为BD是边AC上的高,所以∠BDC=90°,则∠CBD=20°;
(2)在AD上取一点F,使FD=CD,连接FB,分别取AB、FB的中点H、L,连接EH、DL、HL,因为BE是边AC上的中线,所以点E是AC的中点,则EH∥DL∥BC,且EH=DL=BC,所以四边形DEHL是平行四边形,则HL=DE,所以AF=2HL=2DE,即可证明AD﹣CD=2DE.
【解析】(1)解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,且∠A=40°,
∴2∠C+40°=180°,
∴∠C=70°,
∵BD是边AC上的高,
∴BD⊥AC,
∴∠BDC=90°,
∴∠CBD=90°﹣∠C=20°,
∴∠CBD的度数是20°.
(2)证明:在AD上取一点F,使FD=CD,连接FB,分别取AB、FB的中点H、L,连接EH、DL、HL,
∵BE是边AC上的中线,
∴点E是AC的中点,
∴EH∥BC,且EH=BC,DL∥BC,且DL=BC,
∴EH∥DL,且EH=DL,
∴四边形DEHL是平行四边形,
∴HL=DE,
∴AF=2HL=2DE,
∵AF=AD﹣FD=AD﹣CD,
∴AD﹣CD=2DE.
【点睛】此题重点考查等腰三角形的性质、三角形内角和定理、三角形的中线和高、三角形中位线定理、平行四边形的判定与性质等知识,正确地添加辅助线是解题的关键.
27.(2025 台州一模)如图,在△ABC中,AB=AC,点O为BC中点,点D在边AB上,连接OD.
(1)如图1,若OD⊥AB,OE⊥AC于点E,求证:OE=OD;
(2)如图2,已知∠BAC=90°,AB=4,AD=1.若点F在边AC上,OF=OD,求AF的长.
【点拨】(1)由等腰三角形的性质得∠C=∠B,再证明△OCE≌△OBD(AAS),即可得出结论;
(2)连接OA,过点O作OG⊥AB于点G,OH⊥AC于点H,由等腰直角三角形的性质得∠B=∠C=45°,OA平分∠BAC,OA=BC=OB=OC,则OG=OH,AH=CH=AC=2,AG=BG=AB=2,得AH=AG,DG=AG﹣AD=1,再分两种情况,①点F在线段AH上时,证明Rt△OHF≌Rt△OGD(HL),得FH=DG=1,则AF=AH﹣FH=1;②点F在线段CH上时,同理可证Rt△OHF≌Rt△OGD(HL),得FH=DG=1,则AF=AH+FH=3;即可得出结论.
【解析】(1)证明:∵AB=AC,
∴∠C=∠B,
∵OD⊥AB,OE⊥AC,
∴∠ODB=∠OEC=90°,
∵点O为BC中点,
∴OB=OC,
在△OCE和△OBD中,
,
∴△OCE≌△OBD(AAS),
∴OE=OD;
(2)解:如图2,连接OA,过点O作OG⊥AB于点G,OH⊥AC于点H,
则∠OGB=∠OGA=∠OHC=∠OHA=90°,
∵AB=AC=4,∠BAC=90°,点O为BC中点,
∴∠B=∠C=45°,OA平分∠BAC,OA=BC=OB=OC,
∴OG=OH,AH=CH=AC=2,AG=BG=AB=2,
∴AH=AG,
∵AD=1,
∴DG=AG﹣AD=1,
分两种情况:
①点F在线段AH上时,
在Rt△OHF和Rt△OGD中,
,
∴Rt△OHF≌Rt△OGD(HL),
∴FH=DG=1,
∴AF=AH﹣FH=1;
②点F在线段CH上时,
同理可证:Rt△OHF≌Rt△OGD(HL),
∴FH=DG=1,
∴AF=AH+FH=2+1=3;
综上所述,AF的长为1或3.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、等腰三角形的性质、等腰直角三角形的性质、直角三角形斜边上的中线性质以及分类讨论等知识,本题综合性强,熟练掌握等腰三角形的性质,证明三角形全等是解题的关键,属于中考常考题型.
28.(2025 宁波模拟)如图,在△ABC中,CE⊥AB于点E,点D在BC上,连结AD交CE于点F,BC=13,CE=12.
(1)求BE的长;
(2)若∠AFE=45°,AB=CF,求AE的长.
【点拨】(1)根据勾股定理可得答案;
(2)根据题意可得 AE=EF,再设AE=x,可表示CF=12﹣x,AB=5+x,然后根据AB=CF得出方程,求出解即可.
【解析】解:(1)由题意可知:CE⊥AB,BC=13,CE=12,
在Rt△EBC中,由勾股定理得:;
(2)在Rt△AFE中,∠AFE=45°,
∴AE=EF.
设AE=x,则CF=12﹣x,AB=5+x,
∵AB=CF,
∴5+x=12﹣x,
解得,
∴.
【点睛】本题主要考查了勾股定理,解一元一次方程,等腰直角三角形,熟练运用勾股定理解决问题是解答本题的关键.
29.(2025 宁波一模)在△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F.
(1)若△ABC是正三角形,AD=CE,求sin∠BFE的值.
(2)设四边形CEFD的面积为S1,△AFD,△ABF,△BEF的面积分别为S2,S3,S4,求证:S1 S3>S2 S4.
【点拨】(1)证明△ADB≌△CEA(SAS)得到∠1=∠2,那么∠BFE=60°,即可求解sin∠BFE;
(2)连接DE,设S△DEF=x,利用共高三角形面积比化为底之比得到,即,则x S3=S2 S4,而S1>x,即可证明.
【解析】解:(1)如图,△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F,
∵AB=AC,∠BAC=∠1+∠3=∠ACB=60°,
∵AD=CE,
∴△ADB≌△CEA(SAS),
∴∠1=∠2,
∴∠2+∠3=∠BFE=60°,
∴;
(2)证明:连接DE,设S△DEF=x,
根据题意可得:
,
∴,
∴x S3=S2 S4,
∵S1>x,
∴S1 S3>S2 S4.
【点睛】本题考查了求一个角的正弦值,等边三角形的性质,全等三角形的判定与性质,三角形的面积问题,不等式的性质等知识点,熟练掌握各知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题8 几何初步、平行线、三角形
一.选择题
1.(2025 浙江一模)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
2.(2025 浙江一模)将一个含45°角的三角尺和直尺如图放置.若∠1=65°,则∠2=( )
A.20° B.25° C.30° D.35°
3.(2025 嘉兴模拟)在同一平面内,将直尺、直角三角尺(∠CAB=30°)和木工角尺(DE⊥DF)按如图方式摆放,若AC∥DE,则∠1的度数为( )
A.30° B.45° C.60° D.75°
4.(2025 浙江模拟)如图,张师傅将两根木条AB和AC固定在点A处,在木条AB上点O处安装一根能旋转的木条DE.张师傅用量角仪测得∠A=68°,木条DE与AB的夹角∠BOD=80°,要使DE∥AC,木条DE绕点O至少旋转( )
A.10° B.12° C.14° D.16°
5.(2025 西湖区一模)如图,一束光线PO从空气中斜射入长方体玻璃砖发生折射,已知AD∥BC,延长PO交BC于点P',若∠POA=50°,∠P'OQ=25°,则∠OQB的度数为( )
A.45° B.55° C.65° D.75°
6.(2025 衢江区一模)如图,已知两平行线a、b被直线c所截,∠1=37°,则∠2的度数为( )
A.153° B.143° C.63° D.53°
7.(2025 宁波模拟)将两张矩形纸条按如图方式叠放.若∠1=125°,则∠2=( )
A.45° B.55° C.65° D.75°
8.(2025 定海区一模)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
9.(2025 杭州模拟)如图,AD是△ABC的中线,下列说法错误的是( )
A.△ABD和△ACD全等 B.若AD平分∠BAC,则△ABC是等腰三角形
C.若AD⊥BC,则△ABC是等腰三角形 D.若点D到AB和AC的距离相等,则AD⊥BC
10.(2025 庆元县一模)如图,在△ABC中,点D在BC上,∠DAC=∠ADC=2∠B,AC=3,AD=2,则BC的长为( )
A.7 B.6 C.5 D.4
11.(2025 萧山区一模)如图,点C是线段AB上一点(AC>BC),分别以AC,BC为直角边在AB同侧作等腰Rt△ACD和等腰Rt△BCE,连结AE,BD.记S△ACD=S1,S△BCE=S2,S△ADE=S3,S△BDE=S4,若S1﹣S2=20,则S3+S4=( )
A.10 B.15 C.20 D.40
12.(2025 拱墅区一模)若△ABC是锐角三角形,且∠A=60°,则∠B可能的度数是( )
A.10° B.20° C.30° D.40°
13.(2025 宁波一模)如图,在△ABC中,AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,记BD长为x,CE长为y,x>y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B.x+y C.x﹣y D.x2+y2
14.(2025 绍兴一模)如图,Rt△ABC≌Rt△CDE,∠ABC=∠CDE=90°,C在线段BD上,F是AE的中点,连结BF,DF,若AB=1,DE=2,则BF的长是( )
A. B. C. D.
15.(2025 浙江一模)如图,在△ABC中,点D在BC边上,2∠B=∠DAC,CE⊥AD,若AE=DE=2,AC=6,则BC的长为( )
A.10 B. C.8 D.
16.(2025 衢州一模)如图,是人字形钢架屋顶示意图(部分),其中AB=AC=8,AE=BE,且∠B=30°,∠EFB=∠ADB=90°,则DF的长为( )
A. B. C. D.1
二.填空题
17.(2025 湖州一模)把角度转化成度的形式:70°30′= °.
18.(2025 金华模拟)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,则∠ABC的度数为 °.
19.(2025 萧山区一模)如图,AD∥BC,AC平分∠BAD,若∠ABC=110°,则∠CAD= .
20.(2025 浙江模拟)如图,∠B=20°,∠C=31°,∠BPC=123°,则∠A= °.
21.(2025 上城区一模)如图,在△ABC中,BC=4,BD是AC边上的中线,D点到BC的距离为2,则S△ABC= .
22.(2025 浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
23.(2025 拱墅区一模)如图,在△ABC中,∠C=90°,BD是∠ABC的角平分线,点E在BD上,过点E作EF⊥BD,交AB于点F.若BE=4,BF=5,DE=EF,则BC= .
24.(2025 浙江一模)如图,在△ABC中,AD是BC上的中线,BE⊥AC交AD于点F,AF=DF.若,EC=2,则AB的长为 .
25.(2025 杭州一模)等腰三角形的顶角为100°,则它的一个底角度数为 .
三.解答题
26.(2025 拱墅区一模)如图,在△ABC中,AB=AC,BD,BE分别是边AC上的高线和中线.
(1)若∠A=40°,求∠CBD的度数.
(2)求证:AD﹣CD=2DE.
27.(2025 台州一模)如图,在△ABC中,AB=AC,点O为BC中点,点D在边AB上,连接OD.
(1)如图1,若OD⊥AB,OE⊥AC于点E,求证:OE=OD;
(2)如图2,已知∠BAC=90°,AB=4,AD=1.若点F在边AC上,OF=OD,求AF的长.
28.(2025 宁波模拟)如图,在△ABC中,CE⊥AB于点E,点D在BC上,连结AD交CE于点F,BC=13,CE=12.
(1)求BE的长;
(2)若∠AFE=45°,AB=CF,求AE的长.
29.(2025 宁波一模)在△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F.
(1)若△ABC是正三角形,AD=CE,求sin∠BFE的值.
(2)设四边形CEFD的面积为S1,△AFD,△ABF,△BEF的面积分别为S2,S3,S4,求证:S1 S3>S2 S4.
答案与解析
一.选择题
1.(2025 浙江一模)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
【点拨】利用题中“一个角的余角是这个角的2倍”作为相等关系列方程求解即可.
【解析】解:设这个角是x,
则90°﹣x=2x,
解得x=30°.
故选:A.
【点睛】主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180度.解此题的关键是能准确的从图中找出角之间的数量关系,从而计算出结果.
2.(2025 浙江一模)将一个含45°角的三角尺和直尺如图放置.若∠1=65°,则∠2=( )
A.20° B.25° C.30° D.35°
【点拨】根据直尺两边平行,求出∠3的度数,再根据平角的性质,求解即可.
【解析】解:∵直尺对边平行,
∴∠3=∠1=65°,
∴∠2=25°.
故选:B.
【点睛】本题考查平行线的性质.熟练掌握平行线的性质是关键.
3.(2025 嘉兴模拟)在同一平面内,将直尺、直角三角尺(∠CAB=30°)和木工角尺(DE⊥DF)按如图方式摆放,若AC∥DE,则∠1的度数为( )
A.30° B.45° C.60° D.75°
【点拨】先根据AC∥DE求出∠BDE的度数,再结合DE⊥DF即可解决问题.
【解析】解:∵AC∥DE,∠CAB=30°,
∴∠BDE=∠CAB=30°.
又∵DE⊥DF,
∴∠EDF=90°,
∴∠1=180°﹣90°﹣30°=60°.
故选:C.
【点睛】本题主要考查了平行线的性质及垂线,熟知平行线的性质是解题的关键.
4.(2025 浙江模拟)如图,张师傅将两根木条AB和AC固定在点A处,在木条AB上点O处安装一根能旋转的木条DE.张师傅用量角仪测得∠A=68°,木条DE与AB的夹角∠BOD=80°,要使DE∥AC,木条DE绕点O至少旋转( )
A.10° B.12° C.14° D.16°
【点拨】由同位角相等,两直线平行,即可解决问题.
【解析】解:当∠BOD=∠A=68°时,DE∥AC,
∴木条DE绕点O至少逆时针旋转80°﹣68°=12°.
故选:B.
【点睛】本题考查平行线的判定,关键是掌握同位角相等,两直线平行.
5.(2025 西湖区一模)如图,一束光线PO从空气中斜射入长方体玻璃砖发生折射,已知AD∥BC,延长PO交BC于点P',若∠POA=50°,∠P'OQ=25°,则∠OQB的度数为( )
A.45° B.55° C.65° D.75°
【点拨】根据对顶角相等,角的和差关系计算∠DOQ的度数,再应用平行线的性质得到∠OQB的度数即可.
【解析】解:∵∠POA=∠DOP′,
∠POA=50°,
∴∠DOP′=50°,
∵∠DOQ=∠DOP'+∠P'OQ,
∠P′OQ=25°,
∴∠DOQ=50°+25°=75°,
∵AD∥BC,
∴∠OQB=∠DOQ=75°,
∴∠OQB的度数为75°.
故选:D.
【点睛】本题考查了平行线的性质,对顶角、邻补角,熟练掌握相关性质是解题的关键.
6.(2025 衢江区一模)如图,已知两平行线a、b被直线c所截,∠1=37°,则∠2的度数为( )
A.153° B.143° C.63° D.53°
【点拨】由平行线的性质推出∠3=∠1=37°,由邻补角的性质即可求出∠2的度数,
【解析】解:∵a∥b,
∴∠3=∠1=37°,
∴∠2=180°﹣∠3=143°.
故选:B.
【点睛】本题考查平行线的性质,关键是由平行线的性质推出∠3=∠1.
7.(2025 宁波模拟)将两张矩形纸条按如图方式叠放.若∠1=125°,则∠2=( )
A.45° B.55° C.65° D.75°
【点拨】先根据矩形的性质得到AB∥CD,AC∥BD,再根据平行线的性质得到∠3=∠1=125°,∠2+∠3=180°,进而可求解.
【解析】解:如图,
由平行线可知∠3=∠1=125°,∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣125°=55°,
故选:B.
【点睛】本题考查矩形的性质、平行线的性质,熟练掌握平行线的性质是解答的关键.
8.(2025 定海区一模)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
【点拨】根据平行线的性质得到∠1=∠B=68°,由三角形的外角的性质即可得到结论.
【解析】解:如图,∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°,
故选:C.
【点睛】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键.
9.(2025 杭州模拟)如图,AD是△ABC的中线,下列说法错误的是( )
A.△ABD和△ACD全等 B.若AD平分∠BAC,则△ABC是等腰三角形
C.若AD⊥BC,则△ABC是等腰三角形 D.若点D到AB和AC的距离相等,则AD⊥BC
【点拨】根据中线的定义、全等三角形的判定判断A;延长AD至E,使DE=AD,连接CE,证明△ADB≌△EDC,根据全等三角形的性质判断B;根据线段垂直平分线的性质判断C;根据B选项结论判断D.
【解析】解:A、∵AD是△ABC的中线,
∴BD=DC,
但AB与AC的关系不能确定,
∴△ABD和△ACD不一定全等,本选项说法错误,符合题意;
B、如图,延长AD至E,使DE=AD,连接CE,
则△ADB≌△EDC(SAS),
∴AB=CE,∠BAD=∠E,
∴AC=CE,
∴AB=AC,
∴△ABC是等腰三角形,本选项说法正确,不符合题意;
C、∵AD⊥BC,BD=DC,
∴AD是BC的垂直平分线,
∴AB=AC,
∴△ABC是等腰三角形,本选项说法正确,不符合题意;
D、∵点D到AB和AC的距离相等,
∴AD平分∠BAC,
由B选项可知:AB=AC,
∴AD⊥BC,本选项说法正确,不符合题意;
故选:A.
【点睛】本题考查的是三角形的角平分线、中线和高,掌握三角形的中线的定义、全等三角形的判定和性质是解题的关键.
10.(2025 庆元县一模)如图,在△ABC中,点D在BC上,∠DAC=∠ADC=2∠B,AC=3,AD=2,则BC的长为( )
A.7 B.6 C.5 D.4
【点拨】根据∠DAC=∠ADC得DC=AC=3,再根据三角形外角性质及已知条件证明∠B=∠DAB,则BD=AD=2,由此可得出BC的长.
【解析】解:∵∠DAC=∠ADC,AC=3,
∴DC=AC=3,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠DAB,
又∵∠ADC=2∠B,
∴2∠B=∠B+∠DAB,
∴∠B=∠DAB,
∴BD=AD=2,
∴BC=BD+CD=2+3=5.
故选:C.
【点睛】此题主要考查了等腰三角形的判定和性质,熟练掌握等腰三角形的判定和性质是解决问题的关键.
11.(2025 萧山区一模)如图,点C是线段AB上一点(AC>BC),分别以AC,BC为直角边在AB同侧作等腰Rt△ACD和等腰Rt△BCE,连结AE,BD.记S△ACD=S1,S△BCE=S2,S△ADE=S3,S△BDE=S4,若S1﹣S2=20,则S3+S4=( )
A.10 B.15 C.20 D.40
【点拨】依题意设AC=CD=a,BC=CE=b,则DE=CD﹣CE=a﹣b,进而得S1=a2,S2=b2,S3=(a2﹣ab),S4=(ab﹣b2),根据S1﹣S2=20得(a2﹣b2)=20,则S3+S4=(a2﹣b2)=20,据此即可得出答案.
【解析】解:依题意得:△ACD和△BCE都是直角三角形,∠ACD=∠BCE=90°,
∴设AC=CD=a,BC=CE=b,
∴DE=CD﹣CE=a﹣b,
∴S1=a2,S2=b2,S3=a(a﹣b)=(a2﹣ab),S4=b(a﹣b)=(ab﹣b2),
∵S1﹣S2=20,
∴a2﹣b2=20,
∴(a2﹣b2)=20,
∴S3+S4=(a2﹣ab+ab﹣b2)=(a2﹣b2)=20.
故选:C.
【点睛】此题主要考查了等腰直角三角形的性质,三角形的面积,准确试题,熟练掌握等腰直角三角形的性质,三角形的面积公式是解决问题的关键.
12.(2025 拱墅区一模)若△ABC是锐角三角形,且∠A=60°,则∠B可能的度数是( )
A.10° B.20° C.30° D.40°
【点拨】设∠B=x°(x>0),利用三角形内角和定理,可得出∠C=180°﹣60°﹣x°,结合△ABC是锐角三角形,可列出关于x的一元一次不等式组,解之可得出x的取值范围,进而可得出∠B度数的范围,再对照四个选项,即可得出结论.
【解析】解:设∠B=x°(x>0),则∠C=180°﹣60°﹣x°,
根据题意得:,
解得:30<x<90,
∴30°<∠B<90°.
故选:D.
【点睛】本题考查了三角形内角和定理、一元一次不等式组的应用以及三角形,根据各角度数之间的关系,正确列出关于x的一元一次不等式组是解题的关键.
13.(2025 宁波一模)如图,在△ABC中,AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,记BD长为x,CE长为y,x>y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B.x+y C.x﹣y D.x2+y2
【点拨】在CA上截取CF=BD=x,过B作BH⊥AC于H,则EF=x﹣y,证明△FCB和△DBC全等得BF=CD=BE=9,则EH=FH=EF=,由勾股定理得BH2=BF2﹣FH2=BC2﹣CH2,则=,整理得xy=19,由此即可得出答案.
【解析】在CA上截取CF=BD,过点B作BH⊥AC于点H,如图所示:
∵BD长为x,CE长为y,
∴CF=BD=x,
∴EF=CF﹣CE=x﹣y,
∵AB=AC,BC=10,点D,E分别在AB,AC上,CD=BE=9,
∴∠ACB=∠ABC,
在△FCB和△DBC中,,
∴△FCB≌△DBC(SAS),
∴BF=CD=BE=9,
∵BH⊥AC,
∴EH=FH=EF=,
在Rt△BHF和Rt△BHC中,由勾股定理得:BH2=BF2﹣FH2=BC2﹣CH2,
∴=,
整理得:xy=19,
∴当x,y的值发生变化时,代数式xy的值不变,始终等于19.
故选:A.
【点睛】此题主要考查了等腰三角形的性质,解直角三角形,勾股定理,熟练掌握等腰三角形的性质,灵活运用锐角三角函数的定义,勾股定理列代数式是解决问题的关键.
14.(2025 绍兴一模)如图,Rt△ABC≌Rt△CDE,∠ABC=∠CDE=90°,C在线段BD上,F是AE的中点,连结BF,DF,若AB=1,DE=2,则BF的长是( )
A. B. C. D.
【点拨】过点F作FH⊥BD于点H,根据全等三角形的性质得BC=DE=2,AB=CD=1,则BD=3,证明FH是直角梯形ABDE的中位线得FH=(AB+DE)=,BH=DH=BD=,然后在Rt△BHF中,由勾股定理即可求出BF的长.
【解析】解:过点F作FH⊥BD于点H,如图所示:
∵Rt△ABC≌Rt△CDE,AB=1,DE=2,
∴BC=DE=2,AB=CD=1,
∴BD=BC+CD=3,
∵∠ABC=∠CDE=90°,
∴AB⊥BD,DE⊥BD,
∴AB∥DE,
∴四边形ABDE是直角梯形,
∵FH⊥BD,
∴FH∥AB∥DE,
又∵F是AE的中点,
∴FH是直角梯形ABDE的中位线,
∴FH=(AB+DE)=,BH=DH=BD=,
在Rt△BHF中,由勾股定理得:BF===.
故选:D.
【点睛】此题主要考查了全等三角形的性质,勾股定理,熟练掌握全等三角形的性质,梯形的中位线定理,勾股定理是解决问题的关键.
15.(2025 浙江一模)如图,在△ABC中,点D在BC边上,2∠B=∠DAC,CE⊥AD,若AE=DE=2,AC=6,则BC的长为( )
A.10 B. C.8 D.
【点拨】根据线段的垂直平分线的性质得到CD=AC,根据等腰三角形的性质得到∠CDA=∠DAC,根据三角形的外角性质求出∠B=∠DAB,得到DB=DA=4,计算即可.
【解析】解:∵AE=DE=2,CE⊥AD,
∴AD=4,CE是AD的垂直平分线,
∴CD=AC=6,
∴∠CDA=∠DAC,
∵2∠B=∠DAC,
∴2∠B=∠CDA,
∵∠CDA=∠B+∠DAB,
∴∠B=∠DAB,
∴DB=DA=4,
∴BC=DB+DC=4+6=10,
故选:A.
【点睛】本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.
16.(2025 衢州一模)如图,是人字形钢架屋顶示意图(部分),其中AB=AC=8,AE=BE,且∠B=30°,∠EFB=∠ADB=90°,则DF的长为( )
A. B. C. D.1
【点拨】先在Rt△ABD中,利用直角三角形斜边上的中线性质可得DE=AE=BE=4,然后利用含30度角的直角三角形的性质可得AD=4,BD=4,再利用等腰三角形的三线合一性质进行计算即可解答.
【解析】解:∵∠ADB=90°,AE=BE,
∴DE=AE=BE=AB=4,
∵∠B=30°,
∴AD=AB=4,BD=AD=4,
∵∠EFB=90°,
∴BF=DF=BD=2,
故选:B.
【点睛】本题考查了等腰三角形的性质,直角三角形斜边上的中线,含30度角的直角三角形,根据题目的已知条件并结合图形进行分析是解题的关键.
二.填空题
17.(2025 湖州一模)把角度转化成度的形式:70°30′= 70.5 °.
【点拨】根据度分秒的进制进行计算,即可解答.
【解析】解:∵30′=0.5°,∴70°30′=70.5°.
故答案为:70.5.
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
18.(2025 金华模拟)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,则∠ABC的度数为 105 °.
【点拨】根据方向角求出∠EBC,再根据平行线的性质求出∠ABE即可得出答案.
【解析】解:如图:
∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东65°方向行走至点C处,
∴∠DAB=40°,∠CBE=65°,
∵AD∥BE,
∴∠ABE=∠DAB=40°,
∴∠ABC=∠ABE+∠EBC=40°+65°=105°.
故答案为:105.
【点睛】本题考查了方向角,熟练掌握方向角的定义是解题的关键.
19.(2025 萧山区一模)如图,AD∥BC,AC平分∠BAD,若∠ABC=110°,则∠CAD= 35° .
【点拨】根据平行线的性质以及角平分线的定义求解即可.
【解析】解:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠B=110°,
∴∠BAD=180°﹣∠B=70°,
∵AC平分∠BAD,
∴∠CAD=∠BAD=35°,
故答案为:35°.
【点睛】本题考查了平行线的性质,根据题目的已知条件并结合图形进行分析是解题的关键.
20.(2025 浙江模拟)如图,∠B=20°,∠C=31°,∠BPC=123°,则∠A= 72 °.
【点拨】连接AP并延长至点D,利用∠BPD=∠BAP+∠B,∠CPD=∠CAP+∠C,得∠BPC=∠BPD+∠CPD=∠BAP+∠B+∠CAP+∠C=123°,即∠BAC+∠B+∠C=123°,代入∠B=20°,∠C=31°,即可求解.
【解析】解:如图,连接AP并延长至点D,
有由意可得:
∠BPC=∠BPD+∠CPD=∠BAP+∠B+∠CAP+∠C=123°,
∴∠BAC+∠B+∠C=123°,
∵∠B=20°,∠C=31°,
∴∠BAC=123°﹣∠B﹣∠C=72°,
故答案为:72.
【点睛】本题考查三角形的外角的性质,熟练掌握三角形的外角等于和它不相邻的两个内角的和是解题的关键.
21.(2025 上城区一模)如图,在△ABC中,BC=4,BD是AC边上的中线,D点到BC的距离为2,则S△ABC= 8 .
【点拨】首先利用已知条件求出△BDC的面积,然后利用中线的性质即可求出△ABC的面积.
【解析】解:∵在△ABC中,BC=4,D点到BC的距离为2,
∴S△BDC=×BC×2=×4×2=4,
而BD是AC边上的中线,
∴S△ABC=2S△BDC=2×4=8.
故答案为:8.
【点睛】此题主要考查了三角形面积的计算,解题的关键是熟练利用三角形的中线平分三角形面积这个性质解决问题.
22.(2025 浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 16 .
【点拨】根据勾股定理求出AB的长,再分别求出以AC为直径的半圆的面积与以BC为直径的半圆的面积以及以AB为直径的半圆的面积与△ABC的面积,即可求解.
【解析】解:在Rt△ABC中,∠C=90°,
∴AB==4,
以AC为直径的半圆的面积===8π,
以BC为直径的半圆的面积===2π,
以AB为直径的半圆的面积=,
S=16,
∴S阴影=8π+2π+16﹣10π=16,
故答案为:16.
【点睛】本题考查了勾股定理,半圆面积的计算,正确得出阴影部分面积的计算方法是解题的关键.
23.(2025 拱墅区一模)如图,在△ABC中,∠C=90°,BD是∠ABC的角平分线,点E在BD上,过点E作EF⊥BD,交AB于点F.若BE=4,BF=5,DE=EF,则BC= .
【点拨】作DH⊥AB于点H,则∠BHD=∠C=90°,而∠HBD=∠CBD,BD=BD,可根据“AAS”证明△HBD≌△CBD,由∠BEF=90°,BE=4,BF=5,求得DE=EF=3,则BD=7,由cos∠ABD===,求得BH=BD=,则BC=BH=,于是得到问题的答案.
【解析】解:作DH⊥AB于点H,则∠BHD=∠C=90°,
∵BD是∠ABC的角平分线,
∴∠HBD=∠CBD,
∵BD=BD,
∴△HBD≌△CBD(AAS),
∵EF⊥BD于点E,
∴∠BEF=90°,
∵BE=4,BF=5,
∴DE=EF===3,
∴BD=BE+DE=4+3=7,
∵cos∠ABD===,
∴BH=BD=×7=,
∴BC=BH=,
故答案为:.
【点睛】此题重点考查全等三角形的判定与性质、勾股定理、解直角三角形等知识,正确地添加辅助线是解题的关键.
24.(2025 浙江一模)如图,在△ABC中,AD是BC上的中线,BE⊥AC交AD于点F,AF=DF.若,EC=2,则AB的长为 .
【点拨】取EC中点M,连接MD,求出EM=1,判定DM是△BCD的中位线,推出EF∥DM,DM=BE,判定EF是△ADM的中位线,得到DM=2EF=,求出BE=2DM=3,由勾股定理求出AB=.
【解析】解:取EC中点M,连接MD,
∴EM=EC=×2=1,
∵AD是BC上的中线,
∴DM是△BCD的中位线,
∴EF∥DM,DM=BE,
∵AF=FD,
∴AE=EM=1,
∴EF是△ADM的中位线,
∴DM=2EF=2×=,
∴BE=2DM=3,
∵BE⊥AC交AD于点F,
∴AB==.
故答案为:.
【点睛】本题考查三角形中位线定理,勾股定理,关键是取CE中点M,构造三角形的中位线.
25.(2025 杭州一模)等腰三角形的顶角为100°,则它的一个底角度数为 40° .
【点拨】根据等腰三角形的性质和三角形内角和定理即可求解.
【解析】解:因为等腰三角形的顶角为100°,
所以这个等腰三角形的一个底角的度数为 (180°﹣100°)=40°.
故答案为:40°.
【点睛】本题考查了等腰三角形的性质和三角形的内角和定理,注意:三角形的三个内角的和等于180°,等边对等角.
三.解答题
26.(2025 拱墅区一模)如图,在△ABC中,AB=AC,BD,BE分别是边AC上的高线和中线.
(1)若∠A=40°,求∠CBD的度数.
(2)求证:AD﹣CD=2DE.
【点拨】(1)由AB=AC,得∠ABC=∠C,而∠A=40°,所以2∠C+40°=180°,求得∠C=70°,因为BD是边AC上的高,所以∠BDC=90°,则∠CBD=20°;
(2)在AD上取一点F,使FD=CD,连接FB,分别取AB、FB的中点H、L,连接EH、DL、HL,因为BE是边AC上的中线,所以点E是AC的中点,则EH∥DL∥BC,且EH=DL=BC,所以四边形DEHL是平行四边形,则HL=DE,所以AF=2HL=2DE,即可证明AD﹣CD=2DE.
【解析】(1)解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,且∠A=40°,
∴2∠C+40°=180°,
∴∠C=70°,
∵BD是边AC上的高,
∴BD⊥AC,
∴∠BDC=90°,
∴∠CBD=90°﹣∠C=20°,
∴∠CBD的度数是20°.
(2)证明:在AD上取一点F,使FD=CD,连接FB,分别取AB、FB的中点H、L,连接EH、DL、HL,
∵BE是边AC上的中线,
∴点E是AC的中点,
∴EH∥BC,且EH=BC,DL∥BC,且DL=BC,
∴EH∥DL,且EH=DL,
∴四边形DEHL是平行四边形,
∴HL=DE,
∴AF=2HL=2DE,
∵AF=AD﹣FD=AD﹣CD,
∴AD﹣CD=2DE.
【点睛】此题重点考查等腰三角形的性质、三角形内角和定理、三角形的中线和高、三角形中位线定理、平行四边形的判定与性质等知识,正确地添加辅助线是解题的关键.
27.(2025 台州一模)如图,在△ABC中,AB=AC,点O为BC中点,点D在边AB上,连接OD.
(1)如图1,若OD⊥AB,OE⊥AC于点E,求证:OE=OD;
(2)如图2,已知∠BAC=90°,AB=4,AD=1.若点F在边AC上,OF=OD,求AF的长.
【点拨】(1)由等腰三角形的性质得∠C=∠B,再证明△OCE≌△OBD(AAS),即可得出结论;
(2)连接OA,过点O作OG⊥AB于点G,OH⊥AC于点H,由等腰直角三角形的性质得∠B=∠C=45°,OA平分∠BAC,OA=BC=OB=OC,则OG=OH,AH=CH=AC=2,AG=BG=AB=2,得AH=AG,DG=AG﹣AD=1,再分两种情况,①点F在线段AH上时,证明Rt△OHF≌Rt△OGD(HL),得FH=DG=1,则AF=AH﹣FH=1;②点F在线段CH上时,同理可证Rt△OHF≌Rt△OGD(HL),得FH=DG=1,则AF=AH+FH=3;即可得出结论.
【解析】(1)证明:∵AB=AC,
∴∠C=∠B,
∵OD⊥AB,OE⊥AC,
∴∠ODB=∠OEC=90°,
∵点O为BC中点,
∴OB=OC,
在△OCE和△OBD中,
,
∴△OCE≌△OBD(AAS),
∴OE=OD;
(2)解:如图2,连接OA,过点O作OG⊥AB于点G,OH⊥AC于点H,
则∠OGB=∠OGA=∠OHC=∠OHA=90°,
∵AB=AC=4,∠BAC=90°,点O为BC中点,
∴∠B=∠C=45°,OA平分∠BAC,OA=BC=OB=OC,
∴OG=OH,AH=CH=AC=2,AG=BG=AB=2,
∴AH=AG,
∵AD=1,
∴DG=AG﹣AD=1,
分两种情况:
①点F在线段AH上时,
在Rt△OHF和Rt△OGD中,
,
∴Rt△OHF≌Rt△OGD(HL),
∴FH=DG=1,
∴AF=AH﹣FH=1;
②点F在线段CH上时,
同理可证:Rt△OHF≌Rt△OGD(HL),
∴FH=DG=1,
∴AF=AH+FH=2+1=3;
综上所述,AF的长为1或3.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、等腰三角形的性质、等腰直角三角形的性质、直角三角形斜边上的中线性质以及分类讨论等知识,本题综合性强,熟练掌握等腰三角形的性质,证明三角形全等是解题的关键,属于中考常考题型.
28.(2025 宁波模拟)如图,在△ABC中,CE⊥AB于点E,点D在BC上,连结AD交CE于点F,BC=13,CE=12.
(1)求BE的长;
(2)若∠AFE=45°,AB=CF,求AE的长.
【点拨】(1)根据勾股定理可得答案;
(2)根据题意可得 AE=EF,再设AE=x,可表示CF=12﹣x,AB=5+x,然后根据AB=CF得出方程,求出解即可.
【解析】解:(1)由题意可知:CE⊥AB,BC=13,CE=12,
在Rt△EBC中,由勾股定理得:;
(2)在Rt△AFE中,∠AFE=45°,
∴AE=EF.
设AE=x,则CF=12﹣x,AB=5+x,
∵AB=CF,
∴5+x=12﹣x,
解得,
∴.
【点睛】本题主要考查了勾股定理,解一元一次方程,等腰直角三角形,熟练运用勾股定理解决问题是解答本题的关键.
29.(2025 宁波一模)在△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F.
(1)若△ABC是正三角形,AD=CE,求sin∠BFE的值.
(2)设四边形CEFD的面积为S1,△AFD,△ABF,△BEF的面积分别为S2,S3,S4,求证:S1 S3>S2 S4.
【点拨】(1)证明△ADB≌△CEA(SAS)得到∠1=∠2,那么∠BFE=60°,即可求解sin∠BFE;
(2)连接DE,设S△DEF=x,利用共高三角形面积比化为底之比得到,即,则x S3=S2 S4,而S1>x,即可证明.
【解析】解:(1)如图,△ABC中,点D,E分别在边AC,BC上,线段AE,BD相交于点F,
∵AB=AC,∠BAC=∠1+∠3=∠ACB=60°,
∵AD=CE,
∴△ADB≌△CEA(SAS),
∴∠1=∠2,
∴∠2+∠3=∠BFE=60°,
∴;
(2)证明:连接DE,设S△DEF=x,
根据题意可得:
,
∴,
∴x S3=S2 S4,
∵S1>x,
∴S1 S3>S2 S4.
【点睛】本题考查了求一个角的正弦值,等边三角形的性质,全等三角形的判定与性质,三角形的面积问题,不等式的性质等知识点,熟练掌握各知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
