专题9 四边形与尺规作图(含解析)-2025年浙江省中考数学一模试题精编
文档属性
| 名称 | 专题9 四边形与尺规作图(含解析)-2025年浙江省中考数学一模试题精编 |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 17:16:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题9 四边形与尺规作图
一.选择题
1.(2025 嘉兴模拟)如图,AC,BD是菱形ABCD的对角线,则下列结论错误的是( )
A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC
2.(2025 台州一模)如图,在 ABCD中,AC,BD为两条对角线.添加下列一个条件,仍不能判定 ABCD是菱形,这个条件是( )
A.AC⊥BD B.AB⊥BC C.AB=BC D.∠BAC=∠DAC
3.(2025 定海区模拟)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
4.(2025 湖州一模)如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为( )
A.(4,0) B.(﹣2,2) C.(2,﹣1) D.(4,1)
5.(2025 衢州一模)如图,在矩形ABCD中,点E是对角线AC上一点,过点E作FG∥AB分别交AD于F,BC于G,连结BE,DE.记△BEC的面积为s,则四边形BEDC的面积为( )
A. B.2s C. D.
6.(2025 浙江一模)如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
7.(2025 富阳区一模)如图,在矩形ABCD中,AB=4,BC=6,菱形EFGH的三个顶点E,F,H分别在矩形ABCD的边AB,BC,AD上,BE=1.得到如下两个结论:①△AEH面积的最大值为,②点G到BC的距离为3.则( )
A.①②都对 B.①②都错 C.①对②错 D.①错②对
8.(2025 萧山区一模)如图,E是正方形ABCD的边CD上一动点(不与C,D重合),连结AE,以AE为边作正方形AEFG,点M是AF的中点,连结CM.给出下列结论:①;②点B,M,D三点共线,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
9.(2025 温州一模)如图,BD是正方形ABCD的对角线,E为边BC上的动点(不与端点重合),点F在BC的延长线上,且CF=BE,过点F作FG⊥BD于点G,连结AE,EG.则下列比值为定值的是( )
A. B. C. D.
10.(2025 拱墅区模拟)如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
二.填空题
11.(2025 宁波模拟)正十边形一个外角的度数是 .
12.(2025 宁波一模)如图,四边形BCDF是平行四边形,已知∠A=40°,∠ABF=30°,则∠CDE= .
13.(2025 宁波一模)如图,AC,BD为矩形ABCD的对角线,DE⊥AC于点E,∠BDE=20°,则∠ACB的度数为 .
14.(2025 滨江区一模)如图,在△ABC中,AB=AC,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D,连接AD,若∠B=50°,则∠DAC= .
15.(2025 宁波一模)如图,在 ABCD中,∠ABC=45°,O为对角线BD的中点,E为BC上一点,将 ABCD沿OE所在的直线折叠,使点B和点D重合.若AB=AE,OF=1,则AB的长为 .
16.(2025 上城区一模)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且DE=DF,点B关于直线EG的对称点B′在线段BC的延长线上,B′E与BF交于点H.
(1)若点A与点H关于直线BE对称,则tan∠EBA= ;
(2)若,则= .
17.(2025 定海区一模)如图,在Rt△ABC中,∠C=90°,分别以Rt△ABC的三边向外作正方形ACFG,正方形BEDC,正方形ANMB,连结NC交AB于点H.已知正方形ACFG的面积为4,若H为AB中点,则正方形BEDC的面积为 .
18.(2025 宁波一模)已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
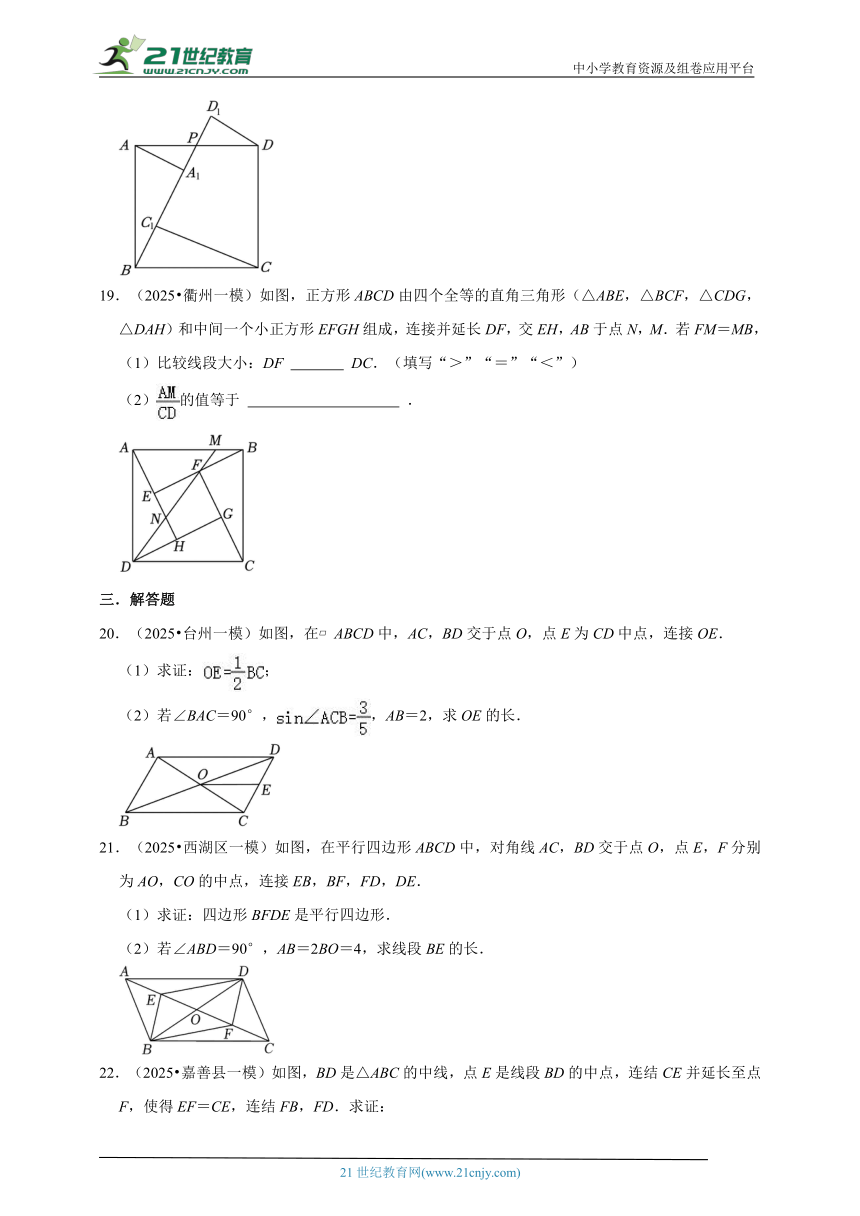
19.(2025 衢州一模)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接并延长DF,交EH,AB于点N,M.若FM=MB,
(1)比较线段大小:DF DC.(填写“>”“=”“<”)
(2)的值等于 .
三.解答题
20.(2025 台州一模)如图,在 ABCD中,AC,BD交于点O,点E为CD中点,连接OE.
(1)求证:;
(2)若∠BAC=90°,,AB=2,求OE的长.
21.(2025 西湖区一模)如图,在平行四边形ABCD中,对角线AC,BD交于点O,点E,F分别为AO,CO的中点,连接EB,BF,FD,DE.
(1)求证:四边形BFDE是平行四边形.
(2)若∠ABD=90°,AB=2BO=4,求线段BE的长.
22.(2025 嘉善县一模)如图,BD是△ABC的中线,点E是线段BD的中点,连结CE并延长至点F,使得EF=CE,连结FB,FD.求证:
(1)BF∥CD;
(2)AB与FD互相平分.
23.(2025 浙江一模)图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点在格点上,分别按要求画出图形:
(1)在图1中画出两个以AB为斜边的直角三角形ABC,且点C在格点上;
(2)在图2中画出一个以AB为对角线的菱形ADBE,且D,E在格点上.
24.(2025 新昌县一模)已知,如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,F是BD的中点,连接CF并延长到E,使FE=CF,连接BE、AE.
(1)求证:四边形AEBD是菱形;
(2)若BC=8,BE=5,求菱形AEBD的面积.
25.(2025 浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,给出了如下作图步骤:
①如图,作直角三角形AOB,其中∠AOB=90°;
②分别延长AO至点C,使CO=AO;延长BO至点D,使DO=BO;
③连结BC,CD,AD,形成四边形ABCD.
请根据上述步骤,解答以下问题:
(1)判断四边形ABCD是否为菱形,并说明理由.
(2)若AC=8,AB=5,求点C到AB的距离.
26.(2025 临安区一模)如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
27.(2025 上城区一模)定义:将一组对角线相同,另一组对角线共线的菱形称为“组合菱形”,内部菱形与外部菱形的共线对角线长之比称为组合比,用k表示.
如图,菱形ABCD和菱形EAFC是组合菱形,其中BD与EF共线,且满足BD:EF=.
(1)组合比k= ;
(2)若BE=2,AB=3,求AC的长;
(3)若∠BAD=∠AEC,求证:∠AEB=30°.
28.(2025 衢州一模)【问题提出】如图,折叠矩形纸片ABCD,使得点B与点A重合,则折痕与边AB,CD的交点E、F将这组对边两等分.如何将矩形纸片的边三等分呢?
【问题思考】如图,将矩形纸片分别沿AC,BF折叠后展平,折痕交于点P.
(1)求证:;
(2)请过点P折叠,在CD上找到一点G,使(要求:在图中画出折痕).
29.(2025 宁波一模)小宁同学按如下步骤作四边形ABCD:①画∠MAN;②以点A为圆心,3cm长为半径画弧,分别交AM,AN于点B,D;③分别以点B,D为圆心,3cm长为半径画弧,两弧交于点C;④连结BC,DC.
(1)求证:四边形ABCD是菱形.
(2)连结BD,若BD=2cm,求四边形ABCD的面积.
30.(2025 金华模拟)尺规作图问题:
如图1,已知∠ABC,用尺规作图方法作以BA,BC为邻边的平行四边形ABCD.
(1)如图2,根据作图痕迹,判定四边形ABCD为平行四边形的依据是什么?
(2)在图1中,请你再作一个平行四边形ABCD(方法与上题不一样,保留作图痕迹,不需要证明).
31.(2025 嘉兴模拟)小红和小明一起研究一个尺规作图问题:
如图1,在 ABCD中,AB<BC,∠B=66°.用直尺和圆规作∠ECB=66°,E是边AD上一点.
小红:如图2,以点C为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
小明:如图3,以点D为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
(1)填空:判断他们的作图方法是否正确.(填“正确”或“错误”)
①小红的作法 ;
②小明的作法 .
(2)请从(1)中任选一项判断,说明理由.(要求:写出推理过程)
32.(2025 衢江区一模)小明研究一道尺规作图题:作△ABC一边BC上的高线.他的作法如下:如图,在△ABC中,AB>AC,以A为圆心,以AC为半径作弧交BC于点D,再分别以C、D为圆心,以大于CD长度为半径作两弧,两弧交于点E,连结AE交BC于点F,则AF为BC边上的高线.
(1)你是否同意小明的作法,如同意请给出证明,不同意请说明理由.
(2)若AB=5,AC=,CF=2,求△ABC的面积.
答案与解析
一.选择题
1.(2025 嘉兴模拟)如图,AC,BD是菱形ABCD的对角线,则下列结论错误的是( )
A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC
【点拨】由菱形的性质可得AB=AD,AC⊥BD,∠BAC=∠DAC,即可求解.
【解析】解:∵AC,BD是菱形ABCD的对角线,
∴AB=AD,AC⊥BD,∠BAC=∠DAC,
故选:C.
【点睛】本题考查了菱形的性质,掌握菱形的性质是解题的关键.
2.(2025 台州一模)如图,在 ABCD中,AC,BD为两条对角线.添加下列一个条件,仍不能判定 ABCD是菱形,这个条件是( )
A.AC⊥BD B.AB⊥BC C.AB=BC D.∠BAC=∠DAC
【点拨】根据菱形的判定定理判断即可.
【解析】解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故不符合题意;
B、∵四边形ABCD是平行四边形,AB⊥BC,
∴ ABCD是矩形,故符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD是菱形,故不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAC=∠DAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ ABCD是菱形,故不符合题意;
故选:B.
【点睛】本题考查了菱形的判定.熟练掌握菱形的判定定理是解题的关键.
3.(2025 定海区模拟)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
【点拨】先求出正六边形的每个内角为120°,再根据六边形MBCDEN的内角和为720°即可求解∠ENM+∠NMB的度数,最后根据邻补角的意义即可求解.
【解析】解:正六边形每个内角为:,
而六边形MBCDEN的内角和也为(6﹣2)×180°=720°,
∴∠B+∠C+∠D+∠E+∠ENM+∠NMB=720°,
∴∠ENM+∠NMB=720°﹣4×120°=240°,
∵β+∠ENM+α+∠NMB=180°×2=360°,
∴α+β=360°﹣240°=120°,
故选:B.
【点睛】本题考查了多边形的内角和,正多边形的每个内角,邻补角,熟练掌握知识点是解决本题的关键.
4.(2025 湖州一模)如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为( )
A.(4,0) B.(﹣2,2) C.(2,﹣1) D.(4,1)
【点拨】作Rt△DBE,将Rt△DBE绕点D顺时针旋转90°至Rt△DB′E′,即可得出B点的坐标.
【解析】解:如图,作Rt△DBE,将Rt△DBE绕点D顺时针旋转90°至Rt△DB′E′,
则DE′=DE=1,E′B′=EB=3,
∴OB′=OE′+E′B′=4,
∴B′(4,0),
∴正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为(4,0).
故选:A.
【点睛】本题考查了旋转的性质和网格当中的旋转作图.旋转的三要素为旋转中心、旋转方向、旋转角度,正确的作出旋转以后的图形是解题的关键.
5.(2025 衢州一模)如图,在矩形ABCD中,点E是对角线AC上一点,过点E作FG∥AB分别交AD于F,BC于G,连结BE,DE.记△BEC的面积为s,则四边形BEDC的面积为( )
A. B.2s C. D.
【点拨】过点E作HL∥BC,交AB于点上,交CD于点L,则四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是矩形,所以S△AFE=S△AHE,S△CLE=S△CGE,S△ADC=S△ABC,由S矩形ELDF+S△AFE+S△CLE=S矩形HBGE+S△AHE+S△CGE,证明S矩形ELDF=S矩形HBGE,推导出S△DEL=S△BEG,S△CEL=S△CEG,则S△DEC=S△BEC=s,所以S四边形BEDC=2s,于是得到问题的答案.
【解析】解:过点E作HL∥BC,交AB于点上,交CD于点L,
∵四边形ABCD是矩形,
∴AD∥BC,CD∥AB,
∵过点E作FG∥AB分别交AD于F,BC于G,
∴HL∥AD,FG∥CD,
∴四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是平行四边形,
∵∠HBG=∠GCL=∠LDF=∠FAH=90°,
∴四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是矩形,
∴S△AFE=S△AHE=AF EF,
同理S△CLE=S△CGE,S△ADC=S△ABC,
∴S矩形ELDF+S△AFE+S△CLE=S矩形HBGE+S△AHE+S△CGE,
∴S矩形ELDF=S矩形HBGE,
∵S△DEL=S△DEF=DF EF=S矩形ELDF,S△BEG=S△BEH=BG EG=S矩形HBGE,
∴S△DEL=S△BEG,
∵S△CEL=S△CEG=CG EG=S矩形EGCL,
∴S△DEC=S△DEL+S△CEL=S△BEG+S△CEG=S△BEC=s,
∴S四边形BEDC=S△DEC+S△BEC=2s,
故选:B.
【点睛】此题重点考查矩形的判定与性质、三角形的面积公式等知识,推导出S矩形ELDF=S矩形HBGE,进而证明S△DEL=S△BEG是解题的关键.
6.(2025 浙江一模)如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
【点拨】把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,首先证明△AFE≌△AGE,进而得到EF=FG,问题即可解决.
【解析】证明:∵四边形ABCD是正方形,
∴AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:
∴∠BAF=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴∠EAF=∠EAG,
∵∠ADG=∠ADC=∠B=90°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
,
∴△AFE≌△AGE(SAS),
∴EF=EG,
即:EF=EG=ED+DG,
∵E为CD的中点,边长为6的正方形ABCD,
∴CD=BC=6,DE=CE=3,∠C=90°,
∴设BF=x,则CF=6﹣x,EF=3+x,
在Rt△CFE中,由勾股定理得:
EF2=CE2+CF2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
即BF=2,
故选:A.
【点睛】本题考查了正方形的性质、全等三角形的判定及其性质的应用,解题的关键是作辅助线,构造全等三角形.
7.(2025 富阳区一模)如图,在矩形ABCD中,AB=4,BC=6,菱形EFGH的三个顶点E,F,H分别在矩形ABCD的边AB,BC,AD上,BE=1.得到如下两个结论:①△AEH面积的最大值为,②点G到BC的距离为3.则( )
A.①②都对 B.①②都错 C.①对②错 D.①错②对
【点拨】根据题意,首先判断△AEH面积的最大时,需EH最大,利用菱形性质,得到需EC最大,从而求出最大的面积,判断结论①正确,利用三角形全等,得到GM=AE=3,判断结论②正确.
【解析】解:如图1,
∵AB=4,BE=1,
∴AE=3,
∵在Rt△AEH中,面积S=AH AE,
又AH=,
∴当EH最大时,AH最大,则△AEH的面积最大,
∵四边形EFGH是菱形,
∴EH=EF,
∴当EF最大时,△AEH的面积最大,
∵当点F在C点时,EF最大,
∴△AEH的面积最大时,菱形为EH'G'C,
∴EH′=,
∴EH'=,
∴AH′=,
∴△AEH的面积最大值S=AH′ AE=×2×3=3,
故结论①正确,符合题意;
如图2,过点G作GM⊥BC,交BC的延长线于M点,
∴GF=EH,∠GMF=∠A=90°,∠GFM=∠AHE,
∴△AEH△≌MGF,
∴GM=AE=3,
∴点G到BC的距离为3,
故结论②正确,符合题意,
综上所述,结论①②都正确,
故选:A.
【点睛】本题考查了矩形、菱形的性质,勾股定理的应用,熟练掌握相关定理是解题的关键.
8.(2025 萧山区一模)如图,E是正方形ABCD的边CD上一动点(不与C,D重合),连结AE,以AE为边作正方形AEFG,点M是AF的中点,连结CM.给出下列结论:①;②点B,M,D三点共线,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
【点拨】①连接GE,MD,MB,过点E作EP∥BC,交MD于点P,先证明△GAB和△EAD全等得BG=DE,∠ABG=∠ADE=90°,由此得点G,B,C三点共线,根据正方形性质得EG经过点M,△AME是等腰直角三角形,由勾股定理得EM=
AE,在Rt△CGE中,根据斜边上中线性质得CM=EM=GM=AM,则CM=AE,据此可对结论①进行判断;
②先证明△ADM和△CDM全等得∠ADM=∠CDM=45°,进而得△EDP是等腰直角三角形,则PE=DE=BG,由此可依据“SAS”判定△BGM和△PEM全等,则∠BMG=∠PME,再根据AF⊥GE得∠BMD=∠AMP+∠BMG+∠AMG=180°,据此可对结论②进行判断,综上所述即可得出答案.
【解析】解:①连接GE,MD,MB,过点E作EP∥BC,交MD于点P,如图所示:
∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD=CD,AG=AE,∠GAE=∠BAD=∠ADE=∠ABC=∠BCD=90°,
∴∠GAB+∠BAE=∠BAE+∠EAD=90°,
∴∠GAB=∠EAD,
在△GAB和△EAD中
,
∴△GAB≌△EAD(SAS),
∴BG=DE,∠ABG=∠ADE=90°,
∴∠ABG+∠ABC=180°,
∴点G,B,C在同一条直线上,
∵AF是正方形AEFG的对角线,点M为AF的中点,
∴EG经过点M,
∴GM=EM=MA=ME,AF⊥GE,
∴△AME是等腰直角三角形,
由勾股定理得:AE==EM,
∴EM=AE,
在Rt△CGE中,CM是斜边GE上的中线,
∴CM=EM=GM=AM,
∴CM=AE,
即2CM=AE,
故结论①对;
②在△ADM和△CDM中,
,
∴△ADM≌△CDM(SSS),
∴∠ADM=∠CDM=∠ADE=45°,
∵EP∥BC,
∴∠DEP=∠BCD=90°,∠BGM=∠PEM,
∴△EDP是等腰直角三角形,
∴PE=DE,
∵BG=DE,
∴BG=PE,
在△BGM和△PEM中,
,
∴△BGM≌△PEM(SAS),
∴∠BMG=∠PME,
∵AF⊥GE,
∴∠AMG=∠AME=∠AMP+∠PME=90°,
∴∠AMP+∠BMG=90°,
∴∠AMP+∠BMG+∠AMG=180°,
即∠BMD=∠AMP+∠BMG+∠AMG=180°,
∴点B,M,D三点共线,
故结论②对,
综上所述:结论①,②都对.
故选:A.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,理解正方形的性质,熟练掌握全等三角形的判定和性质,勾股定理是解决问题的关键,正确地添加辅助线,构造全等三角形是解决问题的难点.
9.(2025 温州一模)如图,BD是正方形ABCD的对角线,E为边BC上的动点(不与端点重合),点F在BC的延长线上,且CF=BE,过点F作FG⊥BD于点G,连结AE,EG.则下列比值为定值的是( )
A. B. C. D.
【点拨】连接AG,CG,证明△ABG和△CBG全等得AG=CG,∠AGB=∠CGB,再证明△GBF是等腰直角三角形得GF=GB,∠F=∠CBG=45°,进而可证明△GCF和△GEB全等,则CG=EB,∠CGF=∠EGB,由此可得出△GAE是等腰直角三角形,再由勾股定理得AE=EG,则=,据此即可得出答案.
【解析】解:连接AG,CG,如图所示:
∵四边形ABCD是正方形,BD是对角线,
∴AB=CB,∠ABG=∠CBG=45°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠AGB=∠CGB,
∵FG⊥BD,
∴∠BGF=90°,
又∵∠CBG=45°,
∴△GBF是等腰直角三角形,
∴GF=GB,∠F=∠CBG=45°,
在△GCF和△GEB中,
,
∴△GCF≌△GEB(SAS),
∴CG=EB,∠CGF=∠EGB,
∴AG=EG,
∴△GAE是等腰三角形,
∵∠AGB=∠CGB,∠CGF=∠EGB,
∴∠AGE=∠AGB+∠EGB=∠CGB+∠CGF=∠BGF=90°,
∴△GAE是等腰直角三角形,
在Rt△GAE中,由勾股定理得:AE==EG,
∴=为定值.
故选:A.
【点睛】此题主要考查了正方形的性质,全等三角形的判定与性质,熟练掌握正方形的性质,全等三角形的判定与性质是解决问题的关键.
10.(2025 拱墅区模拟)如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
【点拨】作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,由平行四边形的性质得AB∥DC,AB=DC,则∠ABM=∠DCN,可证明△ABM≌△DCN,得AM=DN,BM=CN,由BD2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,AC2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,得AC2+BD2=2AB2+2BC2=32,则x2+y2=32,可判断A不符合题意,B不符合题意,C符合题意,D不符合题意,于是得到问题的答案.
【解析】解:作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,则∠ABM=∠N=90°,
∵四边形ABCD是平行四边形,AB=2,BC=2,AC=x,BD=y,
∴AB∥DC,AB=DC,
∴∠ABM=∠DCN,
在△ABM和△DCN中,
,
∴△ABM≌△DCN(AAS),
∴AM=DN,BM=CN,
∴BD2=DN2+BN2=AM2+(BC+CN)2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,
∵AC2=AM2+CM2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,
∴AC2+BD2=2AM2+2BM2+2BC2=2AB2+2BC2=2×22+2×(2)2=32,
∴x2+y2=32,
故A不符合题意,B不符合题意,C符合题意;
假设y2﹣x2=32成立,则x2+y2=y2﹣x2,
求得x=0,不符合题意,
∴y2﹣x2=32不成立,
故D不符合题意,
故选:C.
【点睛】此题重点考查平行四边形的性质、全等三角形的判定与性质、勾股定理等知识,正确地作出辅助线,并且推导出AC2+BD2=2AB2+2BC2是解题的关键.
二.填空题
11.(2025 宁波模拟)正十边形一个外角的度数是 36° .
【点拨】根据多边形的外角和等于360°进行解题即可.
【解析】解:由题可知,
360°÷10=36°.
故答案为:36°.
【点睛】本题考查多边形内角与外角,掌握多边形的外角和等于360°是解题的关键.
12.(2025 宁波一模)如图,四边形BCDF是平行四边形,已知∠A=40°,∠ABF=30°,则∠CDE= 70° .
【点拨】先利用三角形的外角性质求得∠BFD的度数,再根据平行四边形的性质推出FB∥CD,利用平行线的性质,即可求出答案.
【解析】解:∵∠A=40°,∠ABF=30°,
∴∠BFD=∠A+∠ABF=70°,
∵四边形BCDF是平行四边形,
∴FB∥CD,
∴∠CDE=∠BFD=70°,
故答案为:70°.
【点睛】本题主要考查了平行四边形的对边平行的性质,难度不大.
13.(2025 宁波一模)如图,AC,BD为矩形ABCD的对角线,DE⊥AC于点E,∠BDE=20°,则∠ACB的度数为 35° .
【点拨】由外角的性质可得∠BOC=110°,由矩形的性质和等腰三角形的性质可求解.
【解析】解:如图,设AC与BD的交点为O,
∵DE⊥AC,∠BDE=20°,
∴∠BOC=110°,
∵四边形ABCD是矩形,
∴OB=OC=AO=DO,
∴∠ACB=∠OBC=35°,
故答案为:35°.
【点睛】本题考查了矩形的性质,等腰三角形的性质,掌握矩形的性质是解题的关键.
14.(2025 滨江区一模)如图,在△ABC中,AB=AC,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D,连接AD,若∠B=50°,则∠DAC= 30° .
【点拨】由题意,得到DM是线段AB的垂直平分线,利用垂直平分线的性质,得到DA=DB,得到等腰三角形DAB的两底角相等,再利用等腰三角形ABC得到∠C的度数,从而得到结果.
【解析】解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D连接AD,
∴DM是线段AB的垂直平分线,
∴DA=DB,
∴∠BAD=∠B=50°,
∴∠DAC=∠BAC﹣∠BAD=30°.
故答案为:30°.
【点睛】本题考查了作图,掌握垂直平分线的性质,等腰三角形性质的应用是解题的关键.
15.(2025 宁波一模)如图,在 ABCD中,∠ABC=45°,O为对角线BD的中点,E为BC上一点,将 ABCD沿OE所在的直线折叠,使点B和点D重合.若AB=AE,OF=1,则AB的长为 3+ .
【点拨】如图.过点A作AH⊥BC于点H,过点E作EM⊥AD于点M.则四边形AHEM是矩形.想办法证明∠EFO=60°,求出EF,再利用平行线分线段成比例定理求解AF即可.
【解析】解:如图.过点A作AH⊥BC于点H,过点E作EM⊥AD于点M.则四边形AHEM是矩形.
∴AH=EM,
∵AB=AE,
∴∠ABE=∠AEB=45°,
∴∠BAE=90°,
∵AB=AE,AH⊥BE,
∴BH=EH,
∴AH=BH=HE=BE,
∵ED=EB,
∴ED=2AH=2EM,
∵EM⊥AD,
∴∠EDM=30°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CED=∠ADE=30°,
∵EB=ED,
∴∠EBD=∠EDB,
∵∠DEC=∠EBD+∠EDB,
∴∠EBD=∠EDB=15°,
∴∠EFO=∠FEO+∠EBO=60°,
∵EO⊥BD,
∴∠FEO=30°,
∴EF=2OF=2,
设AH=HE=EM=AM=a,则BE=2a,DM=a,
∵AD∥BE,
∴==,
∴AF=1+,
∴AB=AE=1++2=3+.
方法二:倒数第六行开始,设AF=m,则AB=根号3倍m,通过AE=AB可直接求出m和AB长.
故答案为:3+.
【点睛】本题考查平行四边形的性质,翻折变换,解直角三角形,平行线分线段成比例定理,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题.
16.(2025 上城区一模)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且DE=DF,点B关于直线EG的对称点B′在线段BC的延长线上,B′E与BF交于点H.
(1)若点A与点H关于直线BE对称,则tan∠EBA= ;
(2)若,则= .
【点拨】(1)由轴对称可得到∠HEB=∠EBB'=∠EB'B=60°,从而∠ABE=30°,即可解答;
(2)延长BA,B'E,交于点M,设B'E与CD交于点N,由△NFH∽△MBH得到,设FN=a,MB=12a.证明EM=EB,根据“三线合一”得到,设DE=DF=x,则AE=6a﹣x,DN=a+x,NC=5a﹣x,BG=AE=6a﹣x,CB'=6a﹣2x.由△DEN∽△CB'N得到,即,求得x1=2a即可解答.
【解析】解:(1)∵点A与点H关于直线BE对称,
∴∠AEB=∠HEB,
∵点B与点B'关于EG对称,
∴∠EBB'=∠EB'B,
∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBB',
∴∠HEB=∠EBB'=∠EB'B,
∵∠HEB+∠EBB'+∠EB'B=180°,
∴∠HEB=∠EBB'=∠EB'B=60°,
∵在正方形ABCD中,∠ABC=90°,
∴∠ABE=∠ABC﹣∠EBB'=30°,
∴,
故答案为:;
(2)延长BA,B'E,交于点M,设B'E与CD交于点N,
∵在正方形ABCD中,AB∥DC,
∴△NFH∽△MBH,,
∴设FN=a,MB=12a,
∵由(1)有∠ABC=90°,∠BB'E=60°,∠ABE=30°,
∴∠M=180°﹣∠ABC﹣∠BB'E=30°=∠ABE,
∴EM=EB,
∵在正方形ABCD中,DA⊥AB,
∴,
∴在正方形ABCD中,AD=CD=BC=AB=6a,
设DE=DF=x,则AE=AD﹣DE=6a﹣x,DN=FN+DF=a+x,NC=CD﹣DN=6a﹣(a+x)=5a﹣x,
∵点B与点B'关于EG对称,
∴EG⊥BB',BB'=2BG,
∵在正方形ABCD中,∠DAB=∠ABC=90°,
∴四边形AEGB是矩形,
∴BG=AE=6a﹣x,
∴BB'=2BG=2(6a﹣x)=12a﹣2x,
∴CB'=BB'﹣BC=(12a﹣2x)﹣6a=6a﹣2x,
∵AD∥BC,
∴△DEN∽△CB'N,
∴,即,
解得x1=2a,x2=﹣3a(不合题意,舍去),
∴CB'=6a﹣2x=6a﹣4a=2a,
∴,
故答案为:.
【点睛】本题考查正方形的性质,轴对称图形的性质,相似三角形的判定及性质,求锐角三角函数值,解一元二次方程等,综合运用相关知识是解题的关键.
17.(2025 定海区一模)如图,在Rt△ABC中,∠C=90°,分别以Rt△ABC的三边向外作正方形ACFG,正方形BEDC,正方形ANMB,连结NC交AB于点H.已知正方形ACFG的面积为4,若H为AB中点,则正方形BEDC的面积为 .
【点拨】过点C作CP⊥NA交NA的延长线于点P,根据直角三角形斜边中线的性质设CH=AH=BH=a,则AN=AB=2a,NH=,进而得NC=,证明△NAH和△NPC相似得==,则==,由此得AP=,AN=,再由勾股定理得AP2+PC2=AC2,则,继而得,然后在Rt△ABC中,由勾股定理求出BC2即可得出答案.
【解析】解:过点C作CP⊥NA交NA的延长线于点P,如图所示:
∴∠P=90°,
在△ABC中,∠C=90°,点H为AB中点,
∴CH是Rt△ABC斜边AB上的中线,
∴设CH=AH=BH=a,
∴AB=2a,
∵四边形ABMN是正方形,
∴AN=AB=2a,∠NAB=90°,
在Rt△ANH中,由勾股定理得:NH===,
∴NC=NH+CH=,
∵∠NAB=∠P=90°,
∴AH∥NC,
∴△NAH∽△NPC,
∴==,
∴==,
∴PC=,AP=,
∵正方形ACACFG的面积为4,
∴AC2=4,
在Rt△ACP中,由勾股定理得:PC2+AP2=AC2,
∴,
解得:,
在Rt△ABC中,BC2=AB2﹣AC2=(2a)2﹣4=4a2﹣4,
∴BC2==,
∵四边形BEDC是正方形,
∴正方形BEDC的面积为:BC2=.
故答案为:.
【点睛】此题主要考查了正方形的性质,相似三角形的判定和性质,熟练掌握正方形的性质,相似三角形的判定和性质是解决问题的关键.
18.(2025 宁波一模)已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
【点拨】连接BD,PC,根据三角形的面积公式得出,根据S正方形ABCD=S△ABP+S△BCP+S△DPC,推出,当时,m=AA1+CC1+DD1有最小值.
【解析】解:连接BD,PC,
S正方形ABCD=1×1=1,
由勾股定理得:,
∵AB=1,
∴,
∴,
∵,
∴,
∵,
当时,m=AA1+CC1+DD1有最小值,
故答案为:.
【点睛】本题考查了正方形性质,勾股定理,三角形的面积的应用,根据题意得出S正方形ABCD=S△ABP+S△BCP+S△DPC是解题的关键.
19.(2025 衢州一模)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接并延长DF,交EH,AB于点N,M.若FM=MB,
(1)比较线段大小:DF = DC.(填写“>”“=”“<”)
(2)的值等于 .
【点拨】(1)根据正方形ABCD由四个全等的直角三角形,得∠ABE=∠BCF,∠EFC=∠BCD=90°,进而可以解决问题;
(2)设AD=AB=DC=a,MF=MB=x,则AM=AB﹣MB=a﹣x,DM=DF+MF=a+x,根据勾股定理求出a=4x,进而可以解决问题.
【解析】解:(1)∵正方形ABCD由四个全等的直角三角形,
∴∠ABE=∠BCF,∠EFC=∠BCD=90°,
∵FM=MB,
∴∠ABE=∠MFB,
∴∠MFB=∠BCF,
∵∠EFD=∠MFB,
∴∠MFD=∠BCF,
∵∠EFC=∠BCD=90°,
∴∠DFC=∠DCF,
∴DF=DC,
故答案为:=;
(2)设AD=AB=DC=a,MF=MB=x,
则AM=AB﹣MB=a﹣x,DM=DF+MF=a+x,
在Rt△ADM中,由勾股定理得:AD2+AM2=DM2,
a2+(a﹣x)2=(a+x)2,
解得:a=4x(a=0舍去),
∴AM=AB﹣MB=a﹣x=3x,
∴==,
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,全等图形,一元二次方程,解决本题的关键是掌握正方形的性质.
三.解答题
20.(2025 台州一模)如图,在 ABCD中,AC,BD交于点O,点E为CD中点,连接OE.
(1)求证:;
(2)若∠BAC=90°,,AB=2,求OE的长.
【点拨】(1)根据平行四边形的性质得出OB=OD,可推出OE是三角形DBC的中位线,即可得出结论;
(2)根据,AB=2,推出BC的长,再结合(1)的结论即可得出结果.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
又∵点E是CD的中点,
∴OE是三角形DBC的中位线,
∴;
(2)解:∵∠BAC=90°,,AB=2,
∴,
∴BC=,
∴OE=.
【点睛】本题考查了三角形中位线定理,平行四边形的性质,解直角三角形,熟记各性质定理是解题的关键.
21.(2025 西湖区一模)如图,在平行四边形ABCD中,对角线AC,BD交于点O,点E,F分别为AO,CO的中点,连接EB,BF,FD,DE.
(1)求证:四边形BFDE是平行四边形.
(2)若∠ABD=90°,AB=2BO=4,求线段BE的长.
【点拨】(1)由平行四边形的性质可求得OA=OC、OB=OD,再结合E、F为中点,可求得OE=OF,则可证得四边形EBFD为平行四边形;
(2)根据勾股定理求出AO=2,再根据“直角三角形斜边上的中线等于斜边的一半”求解即可.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是AO、CO的中点,
∴OE=OF,
∴四边形BFDE为平行四边形;
(2)解:∵AB=2BO=4,
∴BO=2,
∵∠ABD=90°,
∴AO===2,
∵点E为AO的中点,
∴BE=AO=.
【点睛】本题主要考查平行四边形的性质和判定,掌握平行四边形的对角线互相平分是解题的关键.
22.(2025 嘉善县一模)如图,BD是△ABC的中线,点E是线段BD的中点,连结CE并延长至点F,使得EF=CE,连结FB,FD.求证:
(1)BF∥CD;
(2)AB与FD互相平分.
【点拨】(1)根据“对角线互相平分的四边形是平行四边形”推出四边形FBCD是平行四边形,再根据平行四边形的性质即可得证;
(2)根据“一组对边平行且相等的四边形是平行四边形”推出四边形AFBD是平行四边形,再根据平行四边形的性质即可得证.
【解析】(1)证明:∵点E是线段BD的中点,
∴BE=DE,
又∵EF=CE,
∴四边形FBCD是平行四边形,
∴BF∥CD;
(2)如图,连接AF,
∵四边形FBCD是平行四边形,
∴BD∥CD,BF=CD,
∵BD是△ABC的中线,
∴AD=CD=BF,
∴四边形AFBD是平行四边形,
∴AB与FD互相平分.
【点睛】此题考查了平行四边形的判定与性质,熟记平行四边形的判定定理与性质定理是解题的关键.
23.(2025 浙江一模)图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点在格点上,分别按要求画出图形:
(1)在图1中画出两个以AB为斜边的直角三角形ABC,且点C在格点上;
(2)在图2中画出一个以AB为对角线的菱形ADBE,且D,E在格点上.
【点拨】(1)根据等边三角形的性质及直角三角形的性质作图;
(2)根据等边三角形的性质及菱形的性质作图.
【解析】解:(1)点C、C′即为所求;
(2)菱形ADBE即为所求.
【点睛】本题考查了作图的应用与设计,掌握等边三角形的性质、直角三角形的性质及菱形的性质是解题的关键.
24.(2025 新昌县一模)已知,如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,F是BD的中点,连接CF并延长到E,使FE=CF,连接BE、AE.
(1)求证:四边形AEBD是菱形;
(2)若BC=8,BE=5,求菱形AEBD的面积.
【点拨】(1)证明△CDF≌△EBF(SAS),等CD=BE,∠FCD=∠FEB,则BE∥CD,再证明四边形AEBD是平行四边形,然后由菱形的判定即可得出结论;
(2)连接ED,证明四边形BCDE是平行四边形,得DE=BC=8,再求出AC=2AD=10,进而由勾股定理得AB=6,然后由菱形面积公式列式计算即可.
【解析】(1)证明:∵F是BD的中点,
∴DF=BF,
∵CF=EF,∠CFD=∠EFB,
∴△CDF≌△EBF(SAS),
∴CD=BE,∠FCD=∠FEB,
∴BE∥CD,
∵∠ABC=90°,BD是△ABC的中线,
∴BD=BC=AD=CD,
∴BE=CD=AD,
∴四边形AEBD是平行四边形,
∵BD=AD,
∴平行四边形AEBD是菱形;
(2)解:如图,连接ED,
∵BE∥CD,CD=BE,
∴四边形BCDE是平行四边形,
∴DE=BC=8,
∵AD=BE=5,BD是△ABC中线,
∴AC=2AD=10,
∵∠ABC=90°,BC=8,
∴AB===6,
∴菱形AEBD的面积=AB DE=×6×8=24.
【点睛】本题考查平行四边形的判定与性质,菱形的判定与性质,直角三角形斜边上的中线性质,勾股定理等知识,熟悉掌握菱形的判定与性质是解题的关键.
25.(2025 浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,给出了如下作图步骤:
①如图,作直角三角形AOB,其中∠AOB=90°;
②分别延长AO至点C,使CO=AO;延长BO至点D,使DO=BO;
③连结BC,CD,AD,形成四边形ABCD.
请根据上述步骤,解答以下问题:
(1)判断四边形ABCD是否为菱形,并说明理由.
(2)若AC=8,AB=5,求点C到AB的距离.
【点拨】(1)根据题意可得OA=OC,OB=OD,易证四边形ABCD是平行四边形,再根据∠AOB=90°,推出AC⊥BD,即可证明四边形ABCD是菱形;
(2)由题意易求AO=CO=4,利用勾股定理求出BO=3,得到BD=6,设点C到AB的距离为h,利用菱形ABCD的面积即可求解.
【解析】解:(1)四边形ABCD是菱形,理由如下:
根据题意得OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
(2)∵AB=8,
∴OA=OC=4,
∵∠AOB=90°,AB=5,
在直角三角形AOB中,由勾股定理得:,
∵OB=OD,四边形ABCD是菱形,
∴BD=6,
设点C到AB的距离为h,
∴,
∴,
∴点C到AB的距离为.
【点睛】本题考查平行四边形的判定与性质,菱形的判定与性质,勾股定理,解答本题的关键是熟练掌握菱形的判定与性质.
26.(2025 临安区一模)如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
【点拨】(1)过点F作FK⊥AB于点K,证明四边形ADFK是矩形得AD=FK,DF=AK,则AB=FK,再证明△BAE和△KFH全等,然后根据全等三角形的性质即可得出结论;
(2)根据△BAE和△KFH全等得BE=KH,再根据BE=DF,DF=AK得AK=BE,由此即可得出AH与BE之间的数量关系.
【解析】(1)证明:过点F作FK⊥AB于点K,如图所示:
∴∠FKH=∠FKA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠D=90°,
∴∠FKA=∠BAD=∠D=90°,∠B=∠FKH=90°,
∴四边形ADFK是矩形,
∴AD=FK,DF=AK,
∴AB=FK,
∵FH⊥AE,∠FKH=90°,
∴∠BAE+∠AHF=90°,∠KFH+∠AHF=90°,
∴∠BAE=∠KFH,
在△BAE和△KFH中,
,
∴△BAE≌△KFH(ASA),
∴AE=HF;
(2)解:AH与BE之间的数量关系是,AH=2BE,证明如下:
∵△BAE≌△KFH,
∴BE=KH,
又∵BE=DF,DF=AK,
∴AK=BE,
∴AH=AK+KH=BE+BE=2BE.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,熟练掌握正方形的性质,全等三角形的判定和性质是解决问题的关键.
27.(2025 上城区一模)定义:将一组对角线相同,另一组对角线共线的菱形称为“组合菱形”,内部菱形与外部菱形的共线对角线长之比称为组合比,用k表示.
如图,菱形ABCD和菱形EAFC是组合菱形,其中BD与EF共线,且满足BD:EF=.
(1)组合比k= ;
(2)若BE=2,AB=3,求AC的长;
(3)若∠BAD=∠AEC,求证:∠AEB=30°.
【点拨】(1)由组合比的定义可求解;
(2)由菱形的性质可得AC⊥BD,AO=CO,BO=DO,EO=FO,可求BE=DF=2,可得BO=1,由勾股定理可求AO的长,即可求解;
(3)通过证明△AOB∽△EOA,可得AO=BO,由锐角三角函数可求∠BAO=30°,即可求解.
【解析】(1)解:∵BD:EF=,
∴k=,
故答案为:;
(2)解:如图,连接AC,BD,交于点O,
∵菱形ABCD和菱形EAFC是组合菱形,
∴AC⊥BD,AO=CO,BO=DO,EO=FO,
∴BE=DF=2,
∵BD:EF=,
∴EF=3BD,
∵EF=BE+DF+BD,
∴BE=BD=DF=2,
∴B0=DO=1,
∴AO===2,
∴AC=4;
(3)证明:如图,连接AC,BD,交于点O,
∵菱形ABCD和菱形EAFC是组合菱形,
∴AC⊥BD,AO=CO,BO=DO,EO=FO,∠BAD=2∠BAC,∠AEC=2∠AED,
∵BD:EF=,
∴EF=3BD,
∴EO=3BO,
∵∠BAD=∠AEC,
∴∠BAC=∠AED,
又∵∠AOB=∠AOE=90°,
∴△AOB∽△EOA,
∴,
∴AO=BO,
∴tan∠BAO==,
∴∠BAO=30°,
∴∠AEB=30°.
【点睛】本题是四边形综合题,考查了菱形的性质,勾股定理,相似三角形的判定和性质,锐角三角函数,灵活运用这些性质解决问题是解题的关键.
28.(2025 衢州一模)【问题提出】如图,折叠矩形纸片ABCD,使得点B与点A重合,则折痕与边AB,CD的交点E、F将这组对边两等分.如何将矩形纸片的边三等分呢?
【问题思考】如图,将矩形纸片分别沿AC,BF折叠后展平,折痕交于点P.
(1)求证:;
(2)请过点P折叠,在CD上找到一点G,使(要求:在图中画出折痕).
【点拨】(1)由中点可知CF=,再利用即可得证;
(2)过P画出折痕交CD于点G即可;
【解析】(1)证明:由题意得:E,F分别为AB,CD的中点.
因为四边形ABCD为矩形,
所以AB∥CD,AB=CD,
已知F为CD的中点,
可知,则,
由AB∥CD,得△PCF∽△PAB,
所以,
所以.
(2)解:如图,所示,点G即为所求.
证明:∵CG∥AH,
∴=,
∴AH=2CG,
∴DG=2CG,
∴CG=.
【点睛】本题主要考查了矩形的性质、相似三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
29.(2025 宁波一模)小宁同学按如下步骤作四边形ABCD:①画∠MAN;②以点A为圆心,3cm长为半径画弧,分别交AM,AN于点B,D;③分别以点B,D为圆心,3cm长为半径画弧,两弧交于点C;④连结BC,DC.
(1)求证:四边形ABCD是菱形.
(2)连结BD,若BD=2cm,求四边形ABCD的面积.
【点拨】(1)由作图过程可知AB=AD=CD=BC,则可得四边形ABCD是菱形.
(2)连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2OA,OB==1cm,则OA==,AC=,再根据四边形ABCD的面积为可得答案.
【解析】(1)证明:由作图过程可知,AB=AD=3cm,CD=BC=3cm,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2OA,OB==1cm,
∵AB=3cm,
∴OA===,
∴AC=,
∴四边形ABCD的面积为==(cm2).
【点睛】本题考查作图—基本作图、菱形的判定与性质,熟练掌握菱形的判定与性质是解答本题的关键.
30.(2025 金华模拟)尺规作图问题:
如图1,已知∠ABC,用尺规作图方法作以BA,BC为邻边的平行四边形ABCD.
(1)如图2,根据作图痕迹,判定四边形ABCD为平行四边形的依据是什么?
(2)在图1中,请你再作一个平行四边形ABCD(方法与上题不一样,保留作图痕迹,不需要证明).
【点拨】(1)根据两组对边分别平行的四边形是平行四边形判断即可;
(2)根据两组对边分别相等的四边形是平行四边形作出图形.
【解析】解:(1)如图2中,四边形ABCD是平行四边形的依据是两组对边分别的四边形是平行四边形;
(2)如图1中,四边形ABCD即为所求.
【点睛】本题考查作图﹣复杂作图,平行四边形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
31.(2025 嘉兴模拟)小红和小明一起研究一个尺规作图问题:
如图1,在 ABCD中,AB<BC,∠B=66°.用直尺和圆规作∠ECB=66°,E是边AD上一点.
小红:如图2,以点C为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
小明:如图3,以点D为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
(1)填空:判断他们的作图方法是否正确.(填“正确”或“错误”)
①小红的作法 正确 ;
②小明的作法 错误 .
(2)请从(1)中任选一项判断,说明理由.(要求:写出推理过程)
【点拨】(1)根据题意判断即可;
(2)小红的作法:根据平行四边形的性质得到∠D=∠B=66°,由作图知,CD=CE,得到∠CED=∠D=66°,根据平行线的性质得到;
小明的作法:根据平行四边形的性质得到D=∠B=66°,由作图知,CD=CE,求得∠CED=∠DCE=57°,根据平行线的性质得到∠ECB=∠CED=57°.
【解析】解:(1)①小红的作法正确;
②小明的作法错误;
故答案为:正确,错误;
(2)小红的作法:∵四边形ABCD是平行四边形,
∴∠D=∠B=66°,
由作图知,CD=CE,
∴∠CED=∠D=66°,
∵AD∥BC,
∴∠ECB=∠CED=66°,
故小红的作法正确;
小明的作法:∵四边形ABCD是平行四边形,
∴∠D=∠B=66°,
由作图知,CD=CE,
∴∠CED=∠DCE=57°,
∵AD∥BC,
∴∠ECB=∠CED=57°,
故小明的作法错误.
【点睛】本题考查了作图﹣基本作图,平行四边形的性质,平行线的性质,熟练掌握平行四边形的性质是解题的关键.
32.(2025 衢江区一模)小明研究一道尺规作图题:作△ABC一边BC上的高线.他的作法如下:如图,在△ABC中,AB>AC,以A为圆心,以AC为半径作弧交BC于点D,再分别以C、D为圆心,以大于CD长度为半径作两弧,两弧交于点E,连结AE交BC于点F,则AF为BC边上的高线.
(1)你是否同意小明的作法,如同意请给出证明,不同意请说明理由.
(2)若AB=5,AC=,CF=2,求△ABC的面积.
【点拨】(1)作法正确,证明AE垂直平分线段CD即可;
(2)利用勾股定理去才AF,再利用三角形面积公式求解.
【解析】解:(1)同意.
理由:连接EC,ED.
由作图可知AD=AC,ED=EC,
∴AE垂直平分线段CD,
∴AF⊥BC,即线段AF是△ABC的高;
(2)∵AF⊥BC,AC=,CF=2,
∴AF===3,
∴BF===4,
BC=BF+CF=4+2=6,
∴△ABC的面积= BC AF=×6×3=9.
【点睛】本题考查作图﹣基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题9 四边形与尺规作图
一.选择题
1.(2025 嘉兴模拟)如图,AC,BD是菱形ABCD的对角线,则下列结论错误的是( )
A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC
2.(2025 台州一模)如图,在 ABCD中,AC,BD为两条对角线.添加下列一个条件,仍不能判定 ABCD是菱形,这个条件是( )
A.AC⊥BD B.AB⊥BC C.AB=BC D.∠BAC=∠DAC
3.(2025 定海区模拟)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
4.(2025 湖州一模)如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为( )
A.(4,0) B.(﹣2,2) C.(2,﹣1) D.(4,1)
5.(2025 衢州一模)如图,在矩形ABCD中,点E是对角线AC上一点,过点E作FG∥AB分别交AD于F,BC于G,连结BE,DE.记△BEC的面积为s,则四边形BEDC的面积为( )
A. B.2s C. D.
6.(2025 浙江一模)如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
7.(2025 富阳区一模)如图,在矩形ABCD中,AB=4,BC=6,菱形EFGH的三个顶点E,F,H分别在矩形ABCD的边AB,BC,AD上,BE=1.得到如下两个结论:①△AEH面积的最大值为,②点G到BC的距离为3.则( )
A.①②都对 B.①②都错 C.①对②错 D.①错②对
8.(2025 萧山区一模)如图,E是正方形ABCD的边CD上一动点(不与C,D重合),连结AE,以AE为边作正方形AEFG,点M是AF的中点,连结CM.给出下列结论:①;②点B,M,D三点共线,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
9.(2025 温州一模)如图,BD是正方形ABCD的对角线,E为边BC上的动点(不与端点重合),点F在BC的延长线上,且CF=BE,过点F作FG⊥BD于点G,连结AE,EG.则下列比值为定值的是( )
A. B. C. D.
10.(2025 拱墅区模拟)如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
二.填空题
11.(2025 宁波模拟)正十边形一个外角的度数是 .
12.(2025 宁波一模)如图,四边形BCDF是平行四边形,已知∠A=40°,∠ABF=30°,则∠CDE= .
13.(2025 宁波一模)如图,AC,BD为矩形ABCD的对角线,DE⊥AC于点E,∠BDE=20°,则∠ACB的度数为 .
14.(2025 滨江区一模)如图,在△ABC中,AB=AC,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D,连接AD,若∠B=50°,则∠DAC= .
15.(2025 宁波一模)如图,在 ABCD中,∠ABC=45°,O为对角线BD的中点,E为BC上一点,将 ABCD沿OE所在的直线折叠,使点B和点D重合.若AB=AE,OF=1,则AB的长为 .
16.(2025 上城区一模)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且DE=DF,点B关于直线EG的对称点B′在线段BC的延长线上,B′E与BF交于点H.
(1)若点A与点H关于直线BE对称,则tan∠EBA= ;
(2)若,则= .
17.(2025 定海区一模)如图,在Rt△ABC中,∠C=90°,分别以Rt△ABC的三边向外作正方形ACFG,正方形BEDC,正方形ANMB,连结NC交AB于点H.已知正方形ACFG的面积为4,若H为AB中点,则正方形BEDC的面积为 .
18.(2025 宁波一模)已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
19.(2025 衢州一模)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接并延长DF,交EH,AB于点N,M.若FM=MB,
(1)比较线段大小:DF DC.(填写“>”“=”“<”)
(2)的值等于 .
三.解答题
20.(2025 台州一模)如图,在 ABCD中,AC,BD交于点O,点E为CD中点,连接OE.
(1)求证:;
(2)若∠BAC=90°,,AB=2,求OE的长.
21.(2025 西湖区一模)如图,在平行四边形ABCD中,对角线AC,BD交于点O,点E,F分别为AO,CO的中点,连接EB,BF,FD,DE.
(1)求证:四边形BFDE是平行四边形.
(2)若∠ABD=90°,AB=2BO=4,求线段BE的长.
22.(2025 嘉善县一模)如图,BD是△ABC的中线,点E是线段BD的中点,连结CE并延长至点F,使得EF=CE,连结FB,FD.求证:
(1)BF∥CD;
(2)AB与FD互相平分.
23.(2025 浙江一模)图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点在格点上,分别按要求画出图形:
(1)在图1中画出两个以AB为斜边的直角三角形ABC,且点C在格点上;
(2)在图2中画出一个以AB为对角线的菱形ADBE,且D,E在格点上.
24.(2025 新昌县一模)已知,如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,F是BD的中点,连接CF并延长到E,使FE=CF,连接BE、AE.
(1)求证:四边形AEBD是菱形;
(2)若BC=8,BE=5,求菱形AEBD的面积.
25.(2025 浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,给出了如下作图步骤:
①如图,作直角三角形AOB,其中∠AOB=90°;
②分别延长AO至点C,使CO=AO;延长BO至点D,使DO=BO;
③连结BC,CD,AD,形成四边形ABCD.
请根据上述步骤,解答以下问题:
(1)判断四边形ABCD是否为菱形,并说明理由.
(2)若AC=8,AB=5,求点C到AB的距离.
26.(2025 临安区一模)如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
27.(2025 上城区一模)定义:将一组对角线相同,另一组对角线共线的菱形称为“组合菱形”,内部菱形与外部菱形的共线对角线长之比称为组合比,用k表示.
如图,菱形ABCD和菱形EAFC是组合菱形,其中BD与EF共线,且满足BD:EF=.
(1)组合比k= ;
(2)若BE=2,AB=3,求AC的长;
(3)若∠BAD=∠AEC,求证:∠AEB=30°.
28.(2025 衢州一模)【问题提出】如图,折叠矩形纸片ABCD,使得点B与点A重合,则折痕与边AB,CD的交点E、F将这组对边两等分.如何将矩形纸片的边三等分呢?
【问题思考】如图,将矩形纸片分别沿AC,BF折叠后展平,折痕交于点P.
(1)求证:;
(2)请过点P折叠,在CD上找到一点G,使(要求:在图中画出折痕).
29.(2025 宁波一模)小宁同学按如下步骤作四边形ABCD:①画∠MAN;②以点A为圆心,3cm长为半径画弧,分别交AM,AN于点B,D;③分别以点B,D为圆心,3cm长为半径画弧,两弧交于点C;④连结BC,DC.
(1)求证:四边形ABCD是菱形.
(2)连结BD,若BD=2cm,求四边形ABCD的面积.
30.(2025 金华模拟)尺规作图问题:
如图1,已知∠ABC,用尺规作图方法作以BA,BC为邻边的平行四边形ABCD.
(1)如图2,根据作图痕迹,判定四边形ABCD为平行四边形的依据是什么?
(2)在图1中,请你再作一个平行四边形ABCD(方法与上题不一样,保留作图痕迹,不需要证明).
31.(2025 嘉兴模拟)小红和小明一起研究一个尺规作图问题:
如图1,在 ABCD中,AB<BC,∠B=66°.用直尺和圆规作∠ECB=66°,E是边AD上一点.
小红:如图2,以点C为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
小明:如图3,以点D为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
(1)填空:判断他们的作图方法是否正确.(填“正确”或“错误”)
①小红的作法 ;
②小明的作法 .
(2)请从(1)中任选一项判断,说明理由.(要求:写出推理过程)
32.(2025 衢江区一模)小明研究一道尺规作图题:作△ABC一边BC上的高线.他的作法如下:如图,在△ABC中,AB>AC,以A为圆心,以AC为半径作弧交BC于点D,再分别以C、D为圆心,以大于CD长度为半径作两弧,两弧交于点E,连结AE交BC于点F,则AF为BC边上的高线.
(1)你是否同意小明的作法,如同意请给出证明,不同意请说明理由.
(2)若AB=5,AC=,CF=2,求△ABC的面积.
答案与解析
一.选择题
1.(2025 嘉兴模拟)如图,AC,BD是菱形ABCD的对角线,则下列结论错误的是( )
A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC
【点拨】由菱形的性质可得AB=AD,AC⊥BD,∠BAC=∠DAC,即可求解.
【解析】解:∵AC,BD是菱形ABCD的对角线,
∴AB=AD,AC⊥BD,∠BAC=∠DAC,
故选:C.
【点睛】本题考查了菱形的性质,掌握菱形的性质是解题的关键.
2.(2025 台州一模)如图,在 ABCD中,AC,BD为两条对角线.添加下列一个条件,仍不能判定 ABCD是菱形,这个条件是( )
A.AC⊥BD B.AB⊥BC C.AB=BC D.∠BAC=∠DAC
【点拨】根据菱形的判定定理判断即可.
【解析】解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故不符合题意;
B、∵四边形ABCD是平行四边形,AB⊥BC,
∴ ABCD是矩形,故符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD是菱形,故不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAC=∠DAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ ABCD是菱形,故不符合题意;
故选:B.
【点睛】本题考查了菱形的判定.熟练掌握菱形的判定定理是解题的关键.
3.(2025 定海区模拟)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
【点拨】先求出正六边形的每个内角为120°,再根据六边形MBCDEN的内角和为720°即可求解∠ENM+∠NMB的度数,最后根据邻补角的意义即可求解.
【解析】解:正六边形每个内角为:,
而六边形MBCDEN的内角和也为(6﹣2)×180°=720°,
∴∠B+∠C+∠D+∠E+∠ENM+∠NMB=720°,
∴∠ENM+∠NMB=720°﹣4×120°=240°,
∵β+∠ENM+α+∠NMB=180°×2=360°,
∴α+β=360°﹣240°=120°,
故选:B.
【点睛】本题考查了多边形的内角和,正多边形的每个内角,邻补角,熟练掌握知识点是解决本题的关键.
4.(2025 湖州一模)如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为( )
A.(4,0) B.(﹣2,2) C.(2,﹣1) D.(4,1)
【点拨】作Rt△DBE,将Rt△DBE绕点D顺时针旋转90°至Rt△DB′E′,即可得出B点的坐标.
【解析】解:如图,作Rt△DBE,将Rt△DBE绕点D顺时针旋转90°至Rt△DB′E′,
则DE′=DE=1,E′B′=EB=3,
∴OB′=OE′+E′B′=4,
∴B′(4,0),
∴正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为(4,0).
故选:A.
【点睛】本题考查了旋转的性质和网格当中的旋转作图.旋转的三要素为旋转中心、旋转方向、旋转角度,正确的作出旋转以后的图形是解题的关键.
5.(2025 衢州一模)如图,在矩形ABCD中,点E是对角线AC上一点,过点E作FG∥AB分别交AD于F,BC于G,连结BE,DE.记△BEC的面积为s,则四边形BEDC的面积为( )
A. B.2s C. D.
【点拨】过点E作HL∥BC,交AB于点上,交CD于点L,则四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是矩形,所以S△AFE=S△AHE,S△CLE=S△CGE,S△ADC=S△ABC,由S矩形ELDF+S△AFE+S△CLE=S矩形HBGE+S△AHE+S△CGE,证明S矩形ELDF=S矩形HBGE,推导出S△DEL=S△BEG,S△CEL=S△CEG,则S△DEC=S△BEC=s,所以S四边形BEDC=2s,于是得到问题的答案.
【解析】解:过点E作HL∥BC,交AB于点上,交CD于点L,
∵四边形ABCD是矩形,
∴AD∥BC,CD∥AB,
∵过点E作FG∥AB分别交AD于F,BC于G,
∴HL∥AD,FG∥CD,
∴四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是平行四边形,
∵∠HBG=∠GCL=∠LDF=∠FAH=90°,
∴四边形HBGE、四边形EGCL、四边形ELDF、四边形AHEF都是矩形,
∴S△AFE=S△AHE=AF EF,
同理S△CLE=S△CGE,S△ADC=S△ABC,
∴S矩形ELDF+S△AFE+S△CLE=S矩形HBGE+S△AHE+S△CGE,
∴S矩形ELDF=S矩形HBGE,
∵S△DEL=S△DEF=DF EF=S矩形ELDF,S△BEG=S△BEH=BG EG=S矩形HBGE,
∴S△DEL=S△BEG,
∵S△CEL=S△CEG=CG EG=S矩形EGCL,
∴S△DEC=S△DEL+S△CEL=S△BEG+S△CEG=S△BEC=s,
∴S四边形BEDC=S△DEC+S△BEC=2s,
故选:B.
【点睛】此题重点考查矩形的判定与性质、三角形的面积公式等知识,推导出S矩形ELDF=S矩形HBGE,进而证明S△DEL=S△BEG是解题的关键.
6.(2025 浙江一模)如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
【点拨】把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,首先证明△AFE≌△AGE,进而得到EF=FG,问题即可解决.
【解析】证明:∵四边形ABCD是正方形,
∴AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:
∴∠BAF=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴∠EAF=∠EAG,
∵∠ADG=∠ADC=∠B=90°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
,
∴△AFE≌△AGE(SAS),
∴EF=EG,
即:EF=EG=ED+DG,
∵E为CD的中点,边长为6的正方形ABCD,
∴CD=BC=6,DE=CE=3,∠C=90°,
∴设BF=x,则CF=6﹣x,EF=3+x,
在Rt△CFE中,由勾股定理得:
EF2=CE2+CF2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
即BF=2,
故选:A.
【点睛】本题考查了正方形的性质、全等三角形的判定及其性质的应用,解题的关键是作辅助线,构造全等三角形.
7.(2025 富阳区一模)如图,在矩形ABCD中,AB=4,BC=6,菱形EFGH的三个顶点E,F,H分别在矩形ABCD的边AB,BC,AD上,BE=1.得到如下两个结论:①△AEH面积的最大值为,②点G到BC的距离为3.则( )
A.①②都对 B.①②都错 C.①对②错 D.①错②对
【点拨】根据题意,首先判断△AEH面积的最大时,需EH最大,利用菱形性质,得到需EC最大,从而求出最大的面积,判断结论①正确,利用三角形全等,得到GM=AE=3,判断结论②正确.
【解析】解:如图1,
∵AB=4,BE=1,
∴AE=3,
∵在Rt△AEH中,面积S=AH AE,
又AH=,
∴当EH最大时,AH最大,则△AEH的面积最大,
∵四边形EFGH是菱形,
∴EH=EF,
∴当EF最大时,△AEH的面积最大,
∵当点F在C点时,EF最大,
∴△AEH的面积最大时,菱形为EH'G'C,
∴EH′=,
∴EH'=,
∴AH′=,
∴△AEH的面积最大值S=AH′ AE=×2×3=3,
故结论①正确,符合题意;
如图2,过点G作GM⊥BC,交BC的延长线于M点,
∴GF=EH,∠GMF=∠A=90°,∠GFM=∠AHE,
∴△AEH△≌MGF,
∴GM=AE=3,
∴点G到BC的距离为3,
故结论②正确,符合题意,
综上所述,结论①②都正确,
故选:A.
【点睛】本题考查了矩形、菱形的性质,勾股定理的应用,熟练掌握相关定理是解题的关键.
8.(2025 萧山区一模)如图,E是正方形ABCD的边CD上一动点(不与C,D重合),连结AE,以AE为边作正方形AEFG,点M是AF的中点,连结CM.给出下列结论:①;②点B,M,D三点共线,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
【点拨】①连接GE,MD,MB,过点E作EP∥BC,交MD于点P,先证明△GAB和△EAD全等得BG=DE,∠ABG=∠ADE=90°,由此得点G,B,C三点共线,根据正方形性质得EG经过点M,△AME是等腰直角三角形,由勾股定理得EM=
AE,在Rt△CGE中,根据斜边上中线性质得CM=EM=GM=AM,则CM=AE,据此可对结论①进行判断;
②先证明△ADM和△CDM全等得∠ADM=∠CDM=45°,进而得△EDP是等腰直角三角形,则PE=DE=BG,由此可依据“SAS”判定△BGM和△PEM全等,则∠BMG=∠PME,再根据AF⊥GE得∠BMD=∠AMP+∠BMG+∠AMG=180°,据此可对结论②进行判断,综上所述即可得出答案.
【解析】解:①连接GE,MD,MB,过点E作EP∥BC,交MD于点P,如图所示:
∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD=CD,AG=AE,∠GAE=∠BAD=∠ADE=∠ABC=∠BCD=90°,
∴∠GAB+∠BAE=∠BAE+∠EAD=90°,
∴∠GAB=∠EAD,
在△GAB和△EAD中
,
∴△GAB≌△EAD(SAS),
∴BG=DE,∠ABG=∠ADE=90°,
∴∠ABG+∠ABC=180°,
∴点G,B,C在同一条直线上,
∵AF是正方形AEFG的对角线,点M为AF的中点,
∴EG经过点M,
∴GM=EM=MA=ME,AF⊥GE,
∴△AME是等腰直角三角形,
由勾股定理得:AE==EM,
∴EM=AE,
在Rt△CGE中,CM是斜边GE上的中线,
∴CM=EM=GM=AM,
∴CM=AE,
即2CM=AE,
故结论①对;
②在△ADM和△CDM中,
,
∴△ADM≌△CDM(SSS),
∴∠ADM=∠CDM=∠ADE=45°,
∵EP∥BC,
∴∠DEP=∠BCD=90°,∠BGM=∠PEM,
∴△EDP是等腰直角三角形,
∴PE=DE,
∵BG=DE,
∴BG=PE,
在△BGM和△PEM中,
,
∴△BGM≌△PEM(SAS),
∴∠BMG=∠PME,
∵AF⊥GE,
∴∠AMG=∠AME=∠AMP+∠PME=90°,
∴∠AMP+∠BMG=90°,
∴∠AMP+∠BMG+∠AMG=180°,
即∠BMD=∠AMP+∠BMG+∠AMG=180°,
∴点B,M,D三点共线,
故结论②对,
综上所述:结论①,②都对.
故选:A.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,理解正方形的性质,熟练掌握全等三角形的判定和性质,勾股定理是解决问题的关键,正确地添加辅助线,构造全等三角形是解决问题的难点.
9.(2025 温州一模)如图,BD是正方形ABCD的对角线,E为边BC上的动点(不与端点重合),点F在BC的延长线上,且CF=BE,过点F作FG⊥BD于点G,连结AE,EG.则下列比值为定值的是( )
A. B. C. D.
【点拨】连接AG,CG,证明△ABG和△CBG全等得AG=CG,∠AGB=∠CGB,再证明△GBF是等腰直角三角形得GF=GB,∠F=∠CBG=45°,进而可证明△GCF和△GEB全等,则CG=EB,∠CGF=∠EGB,由此可得出△GAE是等腰直角三角形,再由勾股定理得AE=EG,则=,据此即可得出答案.
【解析】解:连接AG,CG,如图所示:
∵四边形ABCD是正方形,BD是对角线,
∴AB=CB,∠ABG=∠CBG=45°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠AGB=∠CGB,
∵FG⊥BD,
∴∠BGF=90°,
又∵∠CBG=45°,
∴△GBF是等腰直角三角形,
∴GF=GB,∠F=∠CBG=45°,
在△GCF和△GEB中,
,
∴△GCF≌△GEB(SAS),
∴CG=EB,∠CGF=∠EGB,
∴AG=EG,
∴△GAE是等腰三角形,
∵∠AGB=∠CGB,∠CGF=∠EGB,
∴∠AGE=∠AGB+∠EGB=∠CGB+∠CGF=∠BGF=90°,
∴△GAE是等腰直角三角形,
在Rt△GAE中,由勾股定理得:AE==EG,
∴=为定值.
故选:A.
【点睛】此题主要考查了正方形的性质,全等三角形的判定与性质,熟练掌握正方形的性质,全等三角形的判定与性质是解决问题的关键.
10.(2025 拱墅区模拟)如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
【点拨】作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,由平行四边形的性质得AB∥DC,AB=DC,则∠ABM=∠DCN,可证明△ABM≌△DCN,得AM=DN,BM=CN,由BD2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,AC2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,得AC2+BD2=2AB2+2BC2=32,则x2+y2=32,可判断A不符合题意,B不符合题意,C符合题意,D不符合题意,于是得到问题的答案.
【解析】解:作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,则∠ABM=∠N=90°,
∵四边形ABCD是平行四边形,AB=2,BC=2,AC=x,BD=y,
∴AB∥DC,AB=DC,
∴∠ABM=∠DCN,
在△ABM和△DCN中,
,
∴△ABM≌△DCN(AAS),
∴AM=DN,BM=CN,
∴BD2=DN2+BN2=AM2+(BC+CN)2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,
∵AC2=AM2+CM2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,
∴AC2+BD2=2AM2+2BM2+2BC2=2AB2+2BC2=2×22+2×(2)2=32,
∴x2+y2=32,
故A不符合题意,B不符合题意,C符合题意;
假设y2﹣x2=32成立,则x2+y2=y2﹣x2,
求得x=0,不符合题意,
∴y2﹣x2=32不成立,
故D不符合题意,
故选:C.
【点睛】此题重点考查平行四边形的性质、全等三角形的判定与性质、勾股定理等知识,正确地作出辅助线,并且推导出AC2+BD2=2AB2+2BC2是解题的关键.
二.填空题
11.(2025 宁波模拟)正十边形一个外角的度数是 36° .
【点拨】根据多边形的外角和等于360°进行解题即可.
【解析】解:由题可知,
360°÷10=36°.
故答案为:36°.
【点睛】本题考查多边形内角与外角,掌握多边形的外角和等于360°是解题的关键.
12.(2025 宁波一模)如图,四边形BCDF是平行四边形,已知∠A=40°,∠ABF=30°,则∠CDE= 70° .
【点拨】先利用三角形的外角性质求得∠BFD的度数,再根据平行四边形的性质推出FB∥CD,利用平行线的性质,即可求出答案.
【解析】解:∵∠A=40°,∠ABF=30°,
∴∠BFD=∠A+∠ABF=70°,
∵四边形BCDF是平行四边形,
∴FB∥CD,
∴∠CDE=∠BFD=70°,
故答案为:70°.
【点睛】本题主要考查了平行四边形的对边平行的性质,难度不大.
13.(2025 宁波一模)如图,AC,BD为矩形ABCD的对角线,DE⊥AC于点E,∠BDE=20°,则∠ACB的度数为 35° .
【点拨】由外角的性质可得∠BOC=110°,由矩形的性质和等腰三角形的性质可求解.
【解析】解:如图,设AC与BD的交点为O,
∵DE⊥AC,∠BDE=20°,
∴∠BOC=110°,
∵四边形ABCD是矩形,
∴OB=OC=AO=DO,
∴∠ACB=∠OBC=35°,
故答案为:35°.
【点睛】本题考查了矩形的性质,等腰三角形的性质,掌握矩形的性质是解题的关键.
14.(2025 滨江区一模)如图,在△ABC中,AB=AC,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D,连接AD,若∠B=50°,则∠DAC= 30° .
【点拨】由题意,得到DM是线段AB的垂直平分线,利用垂直平分线的性质,得到DA=DB,得到等腰三角形DAB的两底角相等,再利用等腰三角形ABC得到∠C的度数,从而得到结果.
【解析】解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交BC于点D连接AD,
∴DM是线段AB的垂直平分线,
∴DA=DB,
∴∠BAD=∠B=50°,
∴∠DAC=∠BAC﹣∠BAD=30°.
故答案为:30°.
【点睛】本题考查了作图,掌握垂直平分线的性质,等腰三角形性质的应用是解题的关键.
15.(2025 宁波一模)如图,在 ABCD中,∠ABC=45°,O为对角线BD的中点,E为BC上一点,将 ABCD沿OE所在的直线折叠,使点B和点D重合.若AB=AE,OF=1,则AB的长为 3+ .
【点拨】如图.过点A作AH⊥BC于点H,过点E作EM⊥AD于点M.则四边形AHEM是矩形.想办法证明∠EFO=60°,求出EF,再利用平行线分线段成比例定理求解AF即可.
【解析】解:如图.过点A作AH⊥BC于点H,过点E作EM⊥AD于点M.则四边形AHEM是矩形.
∴AH=EM,
∵AB=AE,
∴∠ABE=∠AEB=45°,
∴∠BAE=90°,
∵AB=AE,AH⊥BE,
∴BH=EH,
∴AH=BH=HE=BE,
∵ED=EB,
∴ED=2AH=2EM,
∵EM⊥AD,
∴∠EDM=30°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CED=∠ADE=30°,
∵EB=ED,
∴∠EBD=∠EDB,
∵∠DEC=∠EBD+∠EDB,
∴∠EBD=∠EDB=15°,
∴∠EFO=∠FEO+∠EBO=60°,
∵EO⊥BD,
∴∠FEO=30°,
∴EF=2OF=2,
设AH=HE=EM=AM=a,则BE=2a,DM=a,
∵AD∥BE,
∴==,
∴AF=1+,
∴AB=AE=1++2=3+.
方法二:倒数第六行开始,设AF=m,则AB=根号3倍m,通过AE=AB可直接求出m和AB长.
故答案为:3+.
【点睛】本题考查平行四边形的性质,翻折变换,解直角三角形,平行线分线段成比例定理,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题.
16.(2025 上城区一模)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且DE=DF,点B关于直线EG的对称点B′在线段BC的延长线上,B′E与BF交于点H.
(1)若点A与点H关于直线BE对称,则tan∠EBA= ;
(2)若,则= .
【点拨】(1)由轴对称可得到∠HEB=∠EBB'=∠EB'B=60°,从而∠ABE=30°,即可解答;
(2)延长BA,B'E,交于点M,设B'E与CD交于点N,由△NFH∽△MBH得到,设FN=a,MB=12a.证明EM=EB,根据“三线合一”得到,设DE=DF=x,则AE=6a﹣x,DN=a+x,NC=5a﹣x,BG=AE=6a﹣x,CB'=6a﹣2x.由△DEN∽△CB'N得到,即,求得x1=2a即可解答.
【解析】解:(1)∵点A与点H关于直线BE对称,
∴∠AEB=∠HEB,
∵点B与点B'关于EG对称,
∴∠EBB'=∠EB'B,
∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBB',
∴∠HEB=∠EBB'=∠EB'B,
∵∠HEB+∠EBB'+∠EB'B=180°,
∴∠HEB=∠EBB'=∠EB'B=60°,
∵在正方形ABCD中,∠ABC=90°,
∴∠ABE=∠ABC﹣∠EBB'=30°,
∴,
故答案为:;
(2)延长BA,B'E,交于点M,设B'E与CD交于点N,
∵在正方形ABCD中,AB∥DC,
∴△NFH∽△MBH,,
∴设FN=a,MB=12a,
∵由(1)有∠ABC=90°,∠BB'E=60°,∠ABE=30°,
∴∠M=180°﹣∠ABC﹣∠BB'E=30°=∠ABE,
∴EM=EB,
∵在正方形ABCD中,DA⊥AB,
∴,
∴在正方形ABCD中,AD=CD=BC=AB=6a,
设DE=DF=x,则AE=AD﹣DE=6a﹣x,DN=FN+DF=a+x,NC=CD﹣DN=6a﹣(a+x)=5a﹣x,
∵点B与点B'关于EG对称,
∴EG⊥BB',BB'=2BG,
∵在正方形ABCD中,∠DAB=∠ABC=90°,
∴四边形AEGB是矩形,
∴BG=AE=6a﹣x,
∴BB'=2BG=2(6a﹣x)=12a﹣2x,
∴CB'=BB'﹣BC=(12a﹣2x)﹣6a=6a﹣2x,
∵AD∥BC,
∴△DEN∽△CB'N,
∴,即,
解得x1=2a,x2=﹣3a(不合题意,舍去),
∴CB'=6a﹣2x=6a﹣4a=2a,
∴,
故答案为:.
【点睛】本题考查正方形的性质,轴对称图形的性质,相似三角形的判定及性质,求锐角三角函数值,解一元二次方程等,综合运用相关知识是解题的关键.
17.(2025 定海区一模)如图,在Rt△ABC中,∠C=90°,分别以Rt△ABC的三边向外作正方形ACFG,正方形BEDC,正方形ANMB,连结NC交AB于点H.已知正方形ACFG的面积为4,若H为AB中点,则正方形BEDC的面积为 .
【点拨】过点C作CP⊥NA交NA的延长线于点P,根据直角三角形斜边中线的性质设CH=AH=BH=a,则AN=AB=2a,NH=,进而得NC=,证明△NAH和△NPC相似得==,则==,由此得AP=,AN=,再由勾股定理得AP2+PC2=AC2,则,继而得,然后在Rt△ABC中,由勾股定理求出BC2即可得出答案.
【解析】解:过点C作CP⊥NA交NA的延长线于点P,如图所示:
∴∠P=90°,
在△ABC中,∠C=90°,点H为AB中点,
∴CH是Rt△ABC斜边AB上的中线,
∴设CH=AH=BH=a,
∴AB=2a,
∵四边形ABMN是正方形,
∴AN=AB=2a,∠NAB=90°,
在Rt△ANH中,由勾股定理得:NH===,
∴NC=NH+CH=,
∵∠NAB=∠P=90°,
∴AH∥NC,
∴△NAH∽△NPC,
∴==,
∴==,
∴PC=,AP=,
∵正方形ACACFG的面积为4,
∴AC2=4,
在Rt△ACP中,由勾股定理得:PC2+AP2=AC2,
∴,
解得:,
在Rt△ABC中,BC2=AB2﹣AC2=(2a)2﹣4=4a2﹣4,
∴BC2==,
∵四边形BEDC是正方形,
∴正方形BEDC的面积为:BC2=.
故答案为:.
【点睛】此题主要考查了正方形的性质,相似三角形的判定和性质,熟练掌握正方形的性质,相似三角形的判定和性质是解决问题的关键.
18.(2025 宁波一模)已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
【点拨】连接BD,PC,根据三角形的面积公式得出,根据S正方形ABCD=S△ABP+S△BCP+S△DPC,推出,当时,m=AA1+CC1+DD1有最小值.
【解析】解:连接BD,PC,
S正方形ABCD=1×1=1,
由勾股定理得:,
∵AB=1,
∴,
∴,
∵,
∴,
∵,
当时,m=AA1+CC1+DD1有最小值,
故答案为:.
【点睛】本题考查了正方形性质,勾股定理,三角形的面积的应用,根据题意得出S正方形ABCD=S△ABP+S△BCP+S△DPC是解题的关键.
19.(2025 衢州一模)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接并延长DF,交EH,AB于点N,M.若FM=MB,
(1)比较线段大小:DF = DC.(填写“>”“=”“<”)
(2)的值等于 .
【点拨】(1)根据正方形ABCD由四个全等的直角三角形,得∠ABE=∠BCF,∠EFC=∠BCD=90°,进而可以解决问题;
(2)设AD=AB=DC=a,MF=MB=x,则AM=AB﹣MB=a﹣x,DM=DF+MF=a+x,根据勾股定理求出a=4x,进而可以解决问题.
【解析】解:(1)∵正方形ABCD由四个全等的直角三角形,
∴∠ABE=∠BCF,∠EFC=∠BCD=90°,
∵FM=MB,
∴∠ABE=∠MFB,
∴∠MFB=∠BCF,
∵∠EFD=∠MFB,
∴∠MFD=∠BCF,
∵∠EFC=∠BCD=90°,
∴∠DFC=∠DCF,
∴DF=DC,
故答案为:=;
(2)设AD=AB=DC=a,MF=MB=x,
则AM=AB﹣MB=a﹣x,DM=DF+MF=a+x,
在Rt△ADM中,由勾股定理得:AD2+AM2=DM2,
a2+(a﹣x)2=(a+x)2,
解得:a=4x(a=0舍去),
∴AM=AB﹣MB=a﹣x=3x,
∴==,
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,全等图形,一元二次方程,解决本题的关键是掌握正方形的性质.
三.解答题
20.(2025 台州一模)如图,在 ABCD中,AC,BD交于点O,点E为CD中点,连接OE.
(1)求证:;
(2)若∠BAC=90°,,AB=2,求OE的长.
【点拨】(1)根据平行四边形的性质得出OB=OD,可推出OE是三角形DBC的中位线,即可得出结论;
(2)根据,AB=2,推出BC的长,再结合(1)的结论即可得出结果.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
又∵点E是CD的中点,
∴OE是三角形DBC的中位线,
∴;
(2)解:∵∠BAC=90°,,AB=2,
∴,
∴BC=,
∴OE=.
【点睛】本题考查了三角形中位线定理,平行四边形的性质,解直角三角形,熟记各性质定理是解题的关键.
21.(2025 西湖区一模)如图,在平行四边形ABCD中,对角线AC,BD交于点O,点E,F分别为AO,CO的中点,连接EB,BF,FD,DE.
(1)求证:四边形BFDE是平行四边形.
(2)若∠ABD=90°,AB=2BO=4,求线段BE的长.
【点拨】(1)由平行四边形的性质可求得OA=OC、OB=OD,再结合E、F为中点,可求得OE=OF,则可证得四边形EBFD为平行四边形;
(2)根据勾股定理求出AO=2,再根据“直角三角形斜边上的中线等于斜边的一半”求解即可.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是AO、CO的中点,
∴OE=OF,
∴四边形BFDE为平行四边形;
(2)解:∵AB=2BO=4,
∴BO=2,
∵∠ABD=90°,
∴AO===2,
∵点E为AO的中点,
∴BE=AO=.
【点睛】本题主要考查平行四边形的性质和判定,掌握平行四边形的对角线互相平分是解题的关键.
22.(2025 嘉善县一模)如图,BD是△ABC的中线,点E是线段BD的中点,连结CE并延长至点F,使得EF=CE,连结FB,FD.求证:
(1)BF∥CD;
(2)AB与FD互相平分.
【点拨】(1)根据“对角线互相平分的四边形是平行四边形”推出四边形FBCD是平行四边形,再根据平行四边形的性质即可得证;
(2)根据“一组对边平行且相等的四边形是平行四边形”推出四边形AFBD是平行四边形,再根据平行四边形的性质即可得证.
【解析】(1)证明:∵点E是线段BD的中点,
∴BE=DE,
又∵EF=CE,
∴四边形FBCD是平行四边形,
∴BF∥CD;
(2)如图,连接AF,
∵四边形FBCD是平行四边形,
∴BD∥CD,BF=CD,
∵BD是△ABC的中线,
∴AD=CD=BF,
∴四边形AFBD是平行四边形,
∴AB与FD互相平分.
【点睛】此题考查了平行四边形的判定与性质,熟记平行四边形的判定定理与性质定理是解题的关键.
23.(2025 浙江一模)图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点在格点上,分别按要求画出图形:
(1)在图1中画出两个以AB为斜边的直角三角形ABC,且点C在格点上;
(2)在图2中画出一个以AB为对角线的菱形ADBE,且D,E在格点上.
【点拨】(1)根据等边三角形的性质及直角三角形的性质作图;
(2)根据等边三角形的性质及菱形的性质作图.
【解析】解:(1)点C、C′即为所求;
(2)菱形ADBE即为所求.
【点睛】本题考查了作图的应用与设计,掌握等边三角形的性质、直角三角形的性质及菱形的性质是解题的关键.
24.(2025 新昌县一模)已知,如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,F是BD的中点,连接CF并延长到E,使FE=CF,连接BE、AE.
(1)求证:四边形AEBD是菱形;
(2)若BC=8,BE=5,求菱形AEBD的面积.
【点拨】(1)证明△CDF≌△EBF(SAS),等CD=BE,∠FCD=∠FEB,则BE∥CD,再证明四边形AEBD是平行四边形,然后由菱形的判定即可得出结论;
(2)连接ED,证明四边形BCDE是平行四边形,得DE=BC=8,再求出AC=2AD=10,进而由勾股定理得AB=6,然后由菱形面积公式列式计算即可.
【解析】(1)证明:∵F是BD的中点,
∴DF=BF,
∵CF=EF,∠CFD=∠EFB,
∴△CDF≌△EBF(SAS),
∴CD=BE,∠FCD=∠FEB,
∴BE∥CD,
∵∠ABC=90°,BD是△ABC的中线,
∴BD=BC=AD=CD,
∴BE=CD=AD,
∴四边形AEBD是平行四边形,
∵BD=AD,
∴平行四边形AEBD是菱形;
(2)解:如图,连接ED,
∵BE∥CD,CD=BE,
∴四边形BCDE是平行四边形,
∴DE=BC=8,
∵AD=BE=5,BD是△ABC中线,
∴AC=2AD=10,
∵∠ABC=90°,BC=8,
∴AB===6,
∴菱形AEBD的面积=AB DE=×6×8=24.
【点睛】本题考查平行四边形的判定与性质,菱形的判定与性质,直角三角形斜边上的中线性质,勾股定理等知识,熟悉掌握菱形的判定与性质是解题的关键.
25.(2025 浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,给出了如下作图步骤:
①如图,作直角三角形AOB,其中∠AOB=90°;
②分别延长AO至点C,使CO=AO;延长BO至点D,使DO=BO;
③连结BC,CD,AD,形成四边形ABCD.
请根据上述步骤,解答以下问题:
(1)判断四边形ABCD是否为菱形,并说明理由.
(2)若AC=8,AB=5,求点C到AB的距离.
【点拨】(1)根据题意可得OA=OC,OB=OD,易证四边形ABCD是平行四边形,再根据∠AOB=90°,推出AC⊥BD,即可证明四边形ABCD是菱形;
(2)由题意易求AO=CO=4,利用勾股定理求出BO=3,得到BD=6,设点C到AB的距离为h,利用菱形ABCD的面积即可求解.
【解析】解:(1)四边形ABCD是菱形,理由如下:
根据题意得OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
(2)∵AB=8,
∴OA=OC=4,
∵∠AOB=90°,AB=5,
在直角三角形AOB中,由勾股定理得:,
∵OB=OD,四边形ABCD是菱形,
∴BD=6,
设点C到AB的距离为h,
∴,
∴,
∴点C到AB的距离为.
【点睛】本题考查平行四边形的判定与性质,菱形的判定与性质,勾股定理,解答本题的关键是熟练掌握菱形的判定与性质.
26.(2025 临安区一模)如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
【点拨】(1)过点F作FK⊥AB于点K,证明四边形ADFK是矩形得AD=FK,DF=AK,则AB=FK,再证明△BAE和△KFH全等,然后根据全等三角形的性质即可得出结论;
(2)根据△BAE和△KFH全等得BE=KH,再根据BE=DF,DF=AK得AK=BE,由此即可得出AH与BE之间的数量关系.
【解析】(1)证明:过点F作FK⊥AB于点K,如图所示:
∴∠FKH=∠FKA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠D=90°,
∴∠FKA=∠BAD=∠D=90°,∠B=∠FKH=90°,
∴四边形ADFK是矩形,
∴AD=FK,DF=AK,
∴AB=FK,
∵FH⊥AE,∠FKH=90°,
∴∠BAE+∠AHF=90°,∠KFH+∠AHF=90°,
∴∠BAE=∠KFH,
在△BAE和△KFH中,
,
∴△BAE≌△KFH(ASA),
∴AE=HF;
(2)解:AH与BE之间的数量关系是,AH=2BE,证明如下:
∵△BAE≌△KFH,
∴BE=KH,
又∵BE=DF,DF=AK,
∴AK=BE,
∴AH=AK+KH=BE+BE=2BE.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,熟练掌握正方形的性质,全等三角形的判定和性质是解决问题的关键.
27.(2025 上城区一模)定义:将一组对角线相同,另一组对角线共线的菱形称为“组合菱形”,内部菱形与外部菱形的共线对角线长之比称为组合比,用k表示.
如图,菱形ABCD和菱形EAFC是组合菱形,其中BD与EF共线,且满足BD:EF=.
(1)组合比k= ;
(2)若BE=2,AB=3,求AC的长;
(3)若∠BAD=∠AEC,求证:∠AEB=30°.
【点拨】(1)由组合比的定义可求解;
(2)由菱形的性质可得AC⊥BD,AO=CO,BO=DO,EO=FO,可求BE=DF=2,可得BO=1,由勾股定理可求AO的长,即可求解;
(3)通过证明△AOB∽△EOA,可得AO=BO,由锐角三角函数可求∠BAO=30°,即可求解.
【解析】(1)解:∵BD:EF=,
∴k=,
故答案为:;
(2)解:如图,连接AC,BD,交于点O,
∵菱形ABCD和菱形EAFC是组合菱形,
∴AC⊥BD,AO=CO,BO=DO,EO=FO,
∴BE=DF=2,
∵BD:EF=,
∴EF=3BD,
∵EF=BE+DF+BD,
∴BE=BD=DF=2,
∴B0=DO=1,
∴AO===2,
∴AC=4;
(3)证明:如图,连接AC,BD,交于点O,
∵菱形ABCD和菱形EAFC是组合菱形,
∴AC⊥BD,AO=CO,BO=DO,EO=FO,∠BAD=2∠BAC,∠AEC=2∠AED,
∵BD:EF=,
∴EF=3BD,
∴EO=3BO,
∵∠BAD=∠AEC,
∴∠BAC=∠AED,
又∵∠AOB=∠AOE=90°,
∴△AOB∽△EOA,
∴,
∴AO=BO,
∴tan∠BAO==,
∴∠BAO=30°,
∴∠AEB=30°.
【点睛】本题是四边形综合题,考查了菱形的性质,勾股定理,相似三角形的判定和性质,锐角三角函数,灵活运用这些性质解决问题是解题的关键.
28.(2025 衢州一模)【问题提出】如图,折叠矩形纸片ABCD,使得点B与点A重合,则折痕与边AB,CD的交点E、F将这组对边两等分.如何将矩形纸片的边三等分呢?
【问题思考】如图,将矩形纸片分别沿AC,BF折叠后展平,折痕交于点P.
(1)求证:;
(2)请过点P折叠,在CD上找到一点G,使(要求:在图中画出折痕).
【点拨】(1)由中点可知CF=,再利用即可得证;
(2)过P画出折痕交CD于点G即可;
【解析】(1)证明:由题意得:E,F分别为AB,CD的中点.
因为四边形ABCD为矩形,
所以AB∥CD,AB=CD,
已知F为CD的中点,
可知,则,
由AB∥CD,得△PCF∽△PAB,
所以,
所以.
(2)解:如图,所示,点G即为所求.
证明:∵CG∥AH,
∴=,
∴AH=2CG,
∴DG=2CG,
∴CG=.
【点睛】本题主要考查了矩形的性质、相似三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
29.(2025 宁波一模)小宁同学按如下步骤作四边形ABCD:①画∠MAN;②以点A为圆心,3cm长为半径画弧,分别交AM,AN于点B,D;③分别以点B,D为圆心,3cm长为半径画弧,两弧交于点C;④连结BC,DC.
(1)求证:四边形ABCD是菱形.
(2)连结BD,若BD=2cm,求四边形ABCD的面积.
【点拨】(1)由作图过程可知AB=AD=CD=BC,则可得四边形ABCD是菱形.
(2)连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2OA,OB==1cm,则OA==,AC=,再根据四边形ABCD的面积为可得答案.
【解析】(1)证明:由作图过程可知,AB=AD=3cm,CD=BC=3cm,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2OA,OB==1cm,
∵AB=3cm,
∴OA===,
∴AC=,
∴四边形ABCD的面积为==(cm2).
【点睛】本题考查作图—基本作图、菱形的判定与性质,熟练掌握菱形的判定与性质是解答本题的关键.
30.(2025 金华模拟)尺规作图问题:
如图1,已知∠ABC,用尺规作图方法作以BA,BC为邻边的平行四边形ABCD.
(1)如图2,根据作图痕迹,判定四边形ABCD为平行四边形的依据是什么?
(2)在图1中,请你再作一个平行四边形ABCD(方法与上题不一样,保留作图痕迹,不需要证明).
【点拨】(1)根据两组对边分别平行的四边形是平行四边形判断即可;
(2)根据两组对边分别相等的四边形是平行四边形作出图形.
【解析】解:(1)如图2中,四边形ABCD是平行四边形的依据是两组对边分别的四边形是平行四边形;
(2)如图1中,四边形ABCD即为所求.
【点睛】本题考查作图﹣复杂作图,平行四边形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
31.(2025 嘉兴模拟)小红和小明一起研究一个尺规作图问题:
如图1,在 ABCD中,AB<BC,∠B=66°.用直尺和圆规作∠ECB=66°,E是边AD上一点.
小红:如图2,以点C为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
小明:如图3,以点D为圆心,CD长为半径作弧,交边AD于点E,连接CE,则∠ECB=66°.
(1)填空:判断他们的作图方法是否正确.(填“正确”或“错误”)
①小红的作法 正确 ;
②小明的作法 错误 .
(2)请从(1)中任选一项判断,说明理由.(要求:写出推理过程)
【点拨】(1)根据题意判断即可;
(2)小红的作法:根据平行四边形的性质得到∠D=∠B=66°,由作图知,CD=CE,得到∠CED=∠D=66°,根据平行线的性质得到;
小明的作法:根据平行四边形的性质得到D=∠B=66°,由作图知,CD=CE,求得∠CED=∠DCE=57°,根据平行线的性质得到∠ECB=∠CED=57°.
【解析】解:(1)①小红的作法正确;
②小明的作法错误;
故答案为:正确,错误;
(2)小红的作法:∵四边形ABCD是平行四边形,
∴∠D=∠B=66°,
由作图知,CD=CE,
∴∠CED=∠D=66°,
∵AD∥BC,
∴∠ECB=∠CED=66°,
故小红的作法正确;
小明的作法:∵四边形ABCD是平行四边形,
∴∠D=∠B=66°,
由作图知,CD=CE,
∴∠CED=∠DCE=57°,
∵AD∥BC,
∴∠ECB=∠CED=57°,
故小明的作法错误.
【点睛】本题考查了作图﹣基本作图,平行四边形的性质,平行线的性质,熟练掌握平行四边形的性质是解题的关键.
32.(2025 衢江区一模)小明研究一道尺规作图题:作△ABC一边BC上的高线.他的作法如下:如图,在△ABC中,AB>AC,以A为圆心,以AC为半径作弧交BC于点D,再分别以C、D为圆心,以大于CD长度为半径作两弧,两弧交于点E,连结AE交BC于点F,则AF为BC边上的高线.
(1)你是否同意小明的作法,如同意请给出证明,不同意请说明理由.
(2)若AB=5,AC=,CF=2,求△ABC的面积.
【点拨】(1)作法正确,证明AE垂直平分线段CD即可;
(2)利用勾股定理去才AF,再利用三角形面积公式求解.
【解析】解:(1)同意.
理由:连接EC,ED.
由作图可知AD=AC,ED=EC,
∴AE垂直平分线段CD,
∴AF⊥BC,即线段AF是△ABC的高;
(2)∵AF⊥BC,AC=,CF=2,
∴AF===3,
∴BF===4,
BC=BF+CF=4+2=6,
∴△ABC的面积= BC AF=×6×3=9.
【点睛】本题考查作图﹣基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
