【期末押题卷】期末素养评价预测卷(含解析)2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末押题卷】期末素养评价预测卷(含解析)2024-2025学年六年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 917.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 09:44:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.有两件衣服进价相同,一件比进价高15%出售,另一件打八五折出售,那么商场( )
A.赚了 B.赔了
C.不赚也不赔
2.下面两种量成反比例的是( )
A.圆的半径和面积
B.路程一定,平均速度和时间
C.书的单价一定,买的本数和所付书费
3.如图为一张长方形纸折起来以后的图形,其中∠1=30°,∠2是( )°。
A.30 B.150 C.75
4.一个晴朗的下午,奇奇站在一棵树旁拍照。奇奇的身高是1.5米,他在阳光下的影子长2.5米。此时树的影子比奇奇的影子长5米,这棵树的实际高度约是( )米。
A.3米 B.3.5米 C.4米 D.4.5米
5.下列说法中错误的是( )
A.医生记录病人的体温变化情况选用折线统计图比较合适。
B.1.8是3的倍数,3是1.8的因数。
C.一个三角形三个内角度数的比是5:3:4,这是一个锐角三角形。
D.一个正方形的边长是非0的自然数,它的周长一定是偶数。
6.下面的图形中,( )是正方体的展开图。
A. B. C.
7.下面各图中,能说明乘法分配律的是( )
A.
B.
C.
D.
二.填空题(共10小题)
8.如果甲=2×2×3,乙=2×3×5,那么甲、乙两数的最大公因数是 ,最小公倍数 。
9.一根电线长24m,用去它的,求还剩多少米.列式为 。
10.一个数的最大因数是18,这个数的最小因数是 ,这个数的最小倍数是 。
11.一个三位小数,精确到百分位约是1.88,这个三位小数最小是 ,最大是 。
12.梧桐郡小区为增加小区的绿化率,新铺了一块草坪,形状是平行四边形,如图,这个平行四边形的面积是 平方米。与这个平行四边形等底等高的三角形的面积是 平方米。
13.如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= cm。
14.要使□56÷38的商是两位数,□里最小可以填 ;
要使619÷□7的商是一位数,□里最小可以填 。
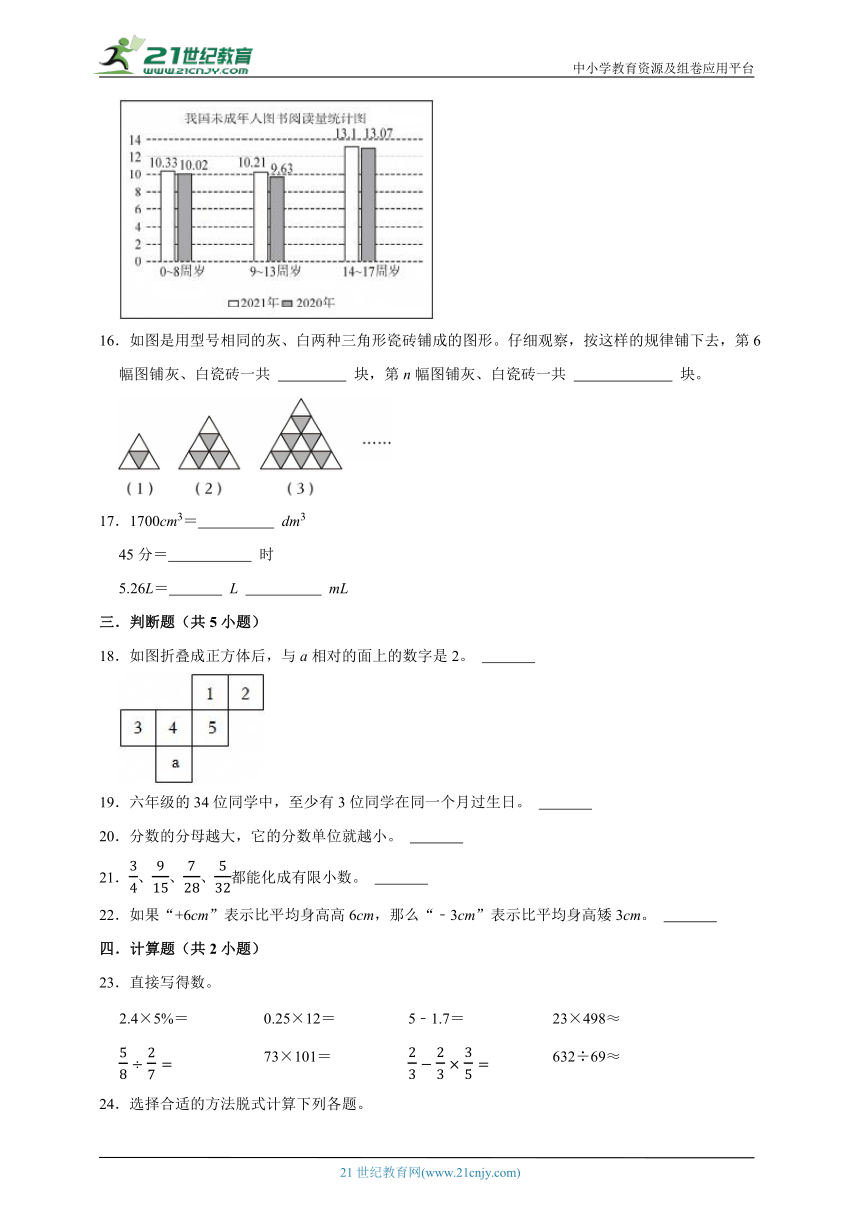
15.如图是我国未成年人图书阅读量统计图。2021年,我国 周岁的图书的阅读量最大。与2020相比,2021年 周岁的阅读量增加最多。
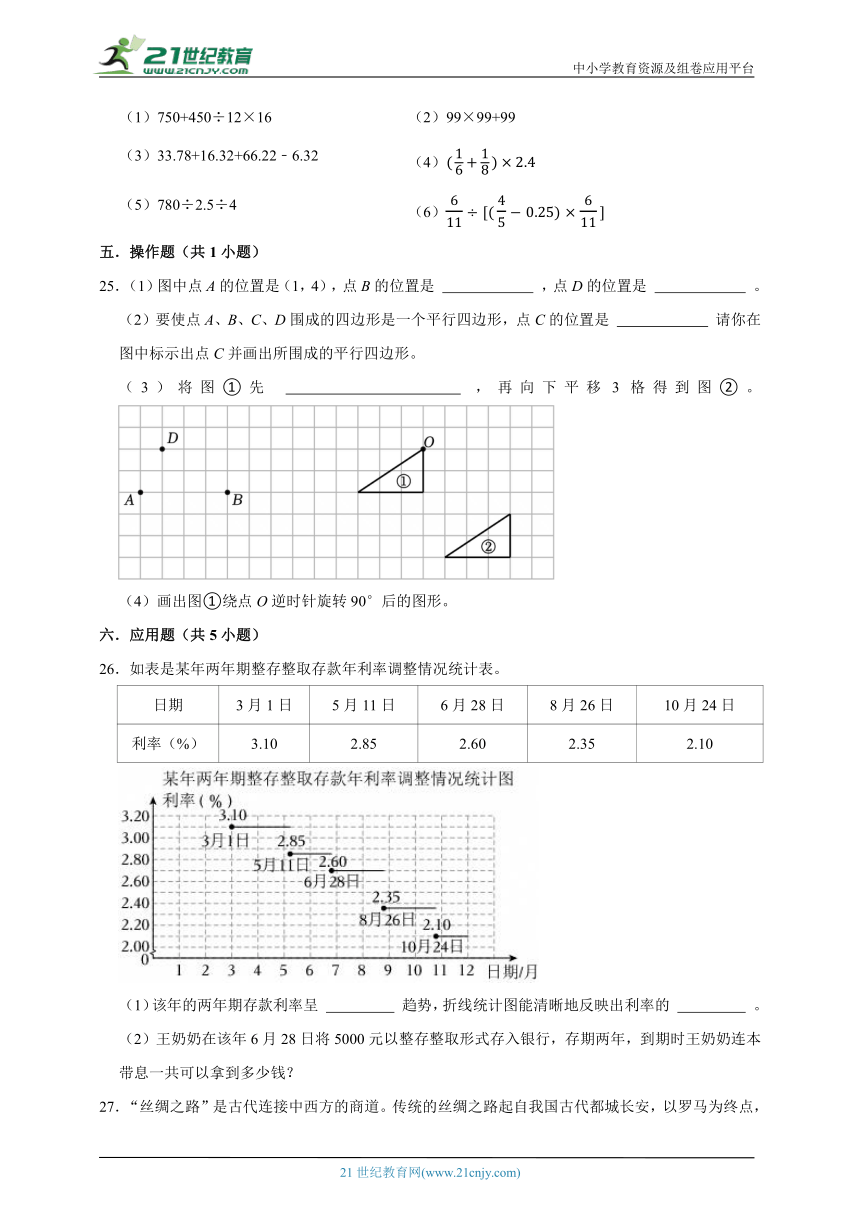
16.如图是用型号相同的灰、白两种三角形瓷砖铺成的图形。仔细观察,按这样的规律铺下去,第6幅图铺灰、白瓷砖一共 块,第n幅图铺灰、白瓷砖一共 块。
17.1700cm3= dm3
45分= 时
5.26L= L mL
三.判断题(共5小题)
18.如图折叠成正方体后,与a相对的面上的数字是2。
19.六年级的34位同学中,至少有3位同学在同一个月过生日。
20.分数的分母越大,它的分数单位就越小。
21.、、、都能化成有限小数。
22.如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。
四.计算题(共2小题)
23.直接写得数。
2.4×5%= 0.25×12= 5﹣1.7= 23×498≈
73×101= 632÷69≈
24.选择合适的方法脱式计算下列各题。
(1)750+450÷12×16 (2)99×99+99
(3)33.78+16.32+66.22﹣6.32 (4)
(5)780÷2.5÷4 (6)
五.操作题(共1小题)
25.(1)图中点A的位置是(1,4),点B的位置是 ,点D的位置是 。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 请你在图中标示出点C并画出所围成的平行四边形。
(3)将图①先 ,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。
六.应用题(共5小题)
26.如表是某年两年期整存整取存款年利率调整情况统计表。
日期 3月1日 5月11日 6月28日 8月26日 10月24日
利率(%) 3.10 2.85 2.60 2.35 2.10
(1)该年的两年期存款利率呈 趋势,折线统计图能清晰地反映出利率的 。
(2)王奶奶在该年6月28日将5000元以整存整取形式存入银行,存期两年,到期时王奶奶连本带息一共可以拿到多少钱?
27.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92厘米,传统的丝绸之路实际全长约为多少千米?
28.一个养殖场,养鸡2500只,养鸭的只数比鸡的只数多。养殖场养鸭多少只?
29.一个圆柱形饼干盒,底面直径是2分米,高是35厘米,要在它的四周贴一圈包装纸(接头处1厘米)。求包装纸的面积。
30.一个圆锥形小麦堆,底面周长是18.84米,高2米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
2024-2025学年六年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
1.有两件衣服进价相同,一件比进价高15%出售,另一件打八五折出售,那么商场( )
A.赚了 B.赔了
C.不赚也不赔
【答案】C
【分析】假设这两件衣服的价钱均为100元,分别计算出利润和赔钱数,再进行比较,即可解答。
【解答】解:假设这两件衣服的价钱均为100元;
100×15%=15(元)
八五折出售即为进价的85%出售。
100×(1﹣85%)
=100×15%
=15(元)
15=15
答:商场不赚也不赔。
故选:C。
【点评】本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。
2.下面两种量成反比例的是( )
A.圆的半径和面积
B.路程一定,平均速度和时间
C.书的单价一定,买的本数和所付书费
【答案】B
【分析】根据各选项中两个相关联的量是乘积一定还是比值一定解答。
【解答】解:选项A中,根据S=πr2,所以圆的半径和面积不成比例。
选项B中,平均速度×时间=路程(一定),所以平均速度和时间成反比例关系。
选项C中,书费÷本数=单价(一定),所以买的本数和所付书费成正比例关系。
故选:B。
【点评】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
3.如图为一张长方形纸折起来以后的图形,其中∠1=30°,∠2是( )°。
A.30 B.150 C.75
【答案】C
【分析】如图,∠1+∠2+∠3=180°,由∠1=30°,得出∠2+∠3=150°,由对折的性质可知∠3=∠2,进一步求得∠2即可。
【解答】解:如图:
由对折的性质可知∠3=∠2,因为,∠1+∠2+∠3=180°,∠1=30°,所以∠2+∠3=150°,∠2=150°÷2=75°。
答:∠2是75°。
故选:C。
【点评】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题,结合题意分析解答即可。
4.一个晴朗的下午,奇奇站在一棵树旁拍照。奇奇的身高是1.5米,他在阳光下的影子长2.5米。此时树的影子比奇奇的影子长5米,这棵树的实际高度约是( )米。
A.3米 B.3.5米 C.4米 D.4.5米
【答案】D
【分析】依据题意可知,身高与影子的长度成正比例,由此列式计算即可。
【解答】解:(2.5+5)×1.5÷2.5
=7.5×1.5÷2.5
=4.5(米)
答:这棵树的实际高度约4.5米。
故选:D。
【点评】本题考查的是正比例的应用。
5.下列说法中错误的是( )
A.医生记录病人的体温变化情况选用折线统计图比较合适。
B.1.8是3的倍数,3是1.8的因数。
C.一个三角形三个内角度数的比是5:3:4,这是一个锐角三角形。
D.一个正方形的边长是非0的自然数,它的周长一定是偶数。
【答案】B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此判断即可。
倍数、因数是针对整数来说的,据此判断即可;
三角形的内角和是180度,又知三个内角的度数的比,运用按比例分配方法求出最大角的度数并判定三角形的类型即可;
根据偶数的意义,假设正方形的边长是n(n是非零自然数),它的周长是4n,4n一定是偶数,由此判断即可。
【解答】解:A.医生记录病人的体温变化情况选用折线统计图比较合适。故原题说法正确;
B.倍数、因数是针对整数来说的,故原题说法错误;
C.180°75°,因为最大的内角是70°,所以这个三角形是锐角三角形,故原题说法正确;
D.边长是非零自然数的正方形,它的周长一定是偶数。所以原题说法正确。
故选:B。
【点评】本题主要考查了统计图的选择、倍数及因数、偶数和三角形内角和及三角形类型的判断。
6.下面的图形中,( )是正方体的展开图。
A. B. C.
【答案】A
【分析】A.展开图符合正方体展开图“一四一”型;B.C.展开图中出现了“田”字型;根据正方体展开图的特征解答。
【解答】解:A.展开图符合正方体展开图“一四一”型,是正方体的展开图;
B.C.展开图中出现了“田”字型,不是正方体的展开图。
故选:A。
【点评】本题考查正方体的展开图,掌握正方体展开图的特征是解题的关键。
7.下面各图中,能说明乘法分配律的是( )
A.
B.
C.
D.
【答案】D
【分析】根据乘法分配律的意义,两个数的和与一个数相乘,可以把这两个加数分别与这个数相乘,然后把两个积相加,结果不变,这叫做乘法分配律;两个数相加,交换加数的位置,和不变;三个数相加,可以先把前两个数相加,也可以把后两个数相加;据此进行分析解答即可。
【解答】解:A.运用加法交换律进行计算,不符合题意;
B.没有运用运算定律,不符合题意;
C.运用加法交换律和结合律进行计算,不符合题意;
D.运用乘法分配律进行计算,符合题意;
故选:D。
【点评】此题考查的目的是理解掌握乘法分配律、加法交换和加法结合律的意义及应用。
二.填空题(共10小题)
8.如果甲=2×2×3,乙=2×3×5,那么甲、乙两数的最大公因数是 6 ,最小公倍数 60 。
【答案】6;60。
【分析】先把要求的两个数分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:因为甲=2×2×3,乙=2×3×5,所以甲、乙两数的最大公因数是2×3=6,最小公倍数2×2×3×5=60。
故答案为:6;60。
【点评】考查了求几个数的最大公因数的方法与最小公倍数的方法:两个数的公有质因数连乘积是最大公因数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数。
9.一根电线长24m,用去它的,求还剩多少米.列式为 24×(1) 。
【答案】24×(1)。
【分析】把这根电线的全长看成单位“1”,用去它的,还剩下全长的1,用全长乘上这个分率就是剩下的长度。
【解答】解:1
列式为:24×(1)
故答案为:24×(1)。
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法。
10.一个数的最大因数是18,这个数的最小因数是 1 ,这个数的最小倍数是 18 。
【答案】1;18。
【分析】一个数的最大因数是它本身,最小因数是1;一个数的最小倍数是它本身。一个数的最大因数是18,所以这个数是18。
【解答】解:一个数的最大因数是18,这个数的最小因数是1,这个数的最小倍数是18。
故答案为:1;18。
【点评】本题考查了找一个数的因数、倍数。
11.一个三位小数,精确到百分位约是1.88,这个三位小数最小是 1.875 ,最大是 1.884 。
【答案】1.875,1.884。
【分析】要考虑1.88是一个三位小数的近似数,有两种情况:“五入”得到的1.88最小是1.875,“四舍”得到的1.88最大是1.884,由此解答问题即可。
【解答】解:一个三位小数,精确到百分位约是1.88,这个三位小数最小是1.875,最大是1.884。
故答案为:1.875,1.884。
【点评】取一个小数的近似数,有两种情况:“四舍”得到的近似数比原数小,“五入”得到的近似数比原数大,根据题的要求灵活掌握解答方法。
12.梧桐郡小区为增加小区的绿化率,新铺了一块草坪,形状是平行四边形,如图,这个平行四边形的面积是 270 平方米。与这个平行四边形等底等高的三角形的面积是 135 平方米。
【答案】270;135。
【分析】根据平行四边形的面积公式计算,平行四边形的面积=底×高;与这个平行四边形等底等高的三角形的面积是这个平行四边形面积的一半,据此解答即可。
【解答】解:18×15=270(平方米)
270÷2=135(平方米)
答:这个平行四边形的面积是270平方米。与这个平行四边形等底等高的三角形的面积是135平方米。
故答案为:270;135。
【点评】熟练掌握平行四边形的面积和三角形的面积公式,是解答本题的关键。
13.如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= 5 cm。
【答案】5。
【分析】读题发现:已知三角形ABC的三条边的长度,按比例算出CE长度即可。
【解答】解:设CE的长度为xcm,则:
8:(12﹣8)=10:x
8:4=10:x
8x=4×10
8x=40
8x÷8=40÷8
x=5
故答案为:5。
【点评】本题考查了图形的放大、比的意义的应用问题,解答本题的关键或突破口在于清楚:AB与BD的长度比等于AC与CE的长度比,据此写出比例再算出结果即可。
14.要使□56÷38的商是两位数,□里最小可以填 4 ;
要使619÷□7的商是一位数,□里最小可以填 6 。
【答案】4;6。
【分析】□56÷38要使商是两位数,被除数前两位数大于或等于除数38;要使619÷□7的商是一位数,被除数前两位数小于除数,然后再进一步解答。
【解答】解:要使□56÷38的商是两位数,□5≥38,□里可以填4,5,6,7,8,9,□里最小可以填4;
要使619÷□7的商是一位数,61<□7,□里可以填6,7,8,9,□里最小可以填6。
故答案为:4;6。
【点评】本题考查除数是两位数的除法的计算及应用。注意计算的准确性。
15.如图是我国未成年人图书阅读量统计图。2021年,我国 14~17 周岁的图书的阅读量最大。与2020相比,2021年 9~13 周岁的阅读量增加最多。
【答案】14~17,9~13。
【分析】从条形统计图可看出,14~17周岁的条形最高,空白和阴影条形相差最多的是9~13周岁。
【解答】解:10.21<10.33<13.1
9.63<10.02<13.07
10.21﹣9.63=0.58
10.33﹣10.02=0.31
13.1﹣13.07=0.03
0.03<0.31<0.58
故答案为:14~17,9~13。
【点评】本题考查了学生从统计图中获取信息的意识。
16.如图是用型号相同的灰、白两种三角形瓷砖铺成的图形。仔细观察,按这样的规律铺下去,第6幅图铺灰、白瓷砖一共 49 块,第n幅图铺灰、白瓷砖一共 (n+1)2 块。
【答案】49,(n+1)2。
【分析】根据观察,图中三角形瓷砖的个数分别是4、9、16……,4=22;9=32;16=42;……由此即可得出第n个图形铺瓷砖的总块数为(n+1)2块。
【解答】解:根据题干得出图中三角形瓷砖的个数分别是4=22;9=32;16=42;……则第n个图形铺瓷砖的总块数为(n+1)2块;
(6+1)2=49(个)
第6幅图铺灰、白瓷砖一共49块,第n幅图铺灰、白瓷砖一共(n+1)2块。
故答案为:49,(n+1)2。
【点评】由题干中的图形的排列以及个数特点,得出瓷砖的排列规律是解决此类问题的关键。
17.1700cm3= 1.7 dm3
45分= 0.75 时
5.26L= 5 L 260 mL
【答案】1.7;0.75;5;260。
【分析】根据1立方分米=1000立方厘米,1小时=60分,1升=1000毫升,解答此题即可。
【解答】解:1700cm3=1.7dm3
45分=0.75时
5.26L=5L260mL
故答案为:1.7;0.75;5;260。
【点评】熟练掌握体积单位、时间单位、锐角单位的换算,是解答此题的关键。
三.判断题(共5小题)
18.如图折叠成正方体后,与a相对的面上的数字是2。 ×
【答案】×
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣3﹣2”型,折叠成正方体后,数字1与字母a相对,2与4相对,3与5相对。
【解答】解:如图:
折叠成正方体后,与a相对的面上的数字是1。
原题说法错误。
故答案为:×。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
19.六年级的34位同学中,至少有3位同学在同一个月过生日。 √
【答案】√
【分析】一年有12个月,把12个月看作12个抽屉,34位同学看作物体个数,根据抽屉原理得:34÷12=2……10;则至少有:2+1=3(位)在同一个月过生日。
【解答】解:建立抽屉:一年有12个月分别看做12个抽屉,
34÷12=2(位)……10(位)
2+1=3(位)
答:至少有3位同学在同一个月过生日。
故答案为:√。
【点评】此题属于典型的抽屉原理习题,解答此类题的关键是找出把谁看作“抽屉个数”,把谁看作“物体个数”,然后根据抽屉原理解答即可。
20.分数的分母越大,它的分数单位就越小。 √
【答案】√
【分析】把一个整体平均分成若干份,其中的1份就是几分之一,也就是这个分数的分数单位,平均分的份数越多,它的分母就越大,每份的数量就越小,也就是份数单位就越小,由此判断。
【解答】解:分数的分母越大,每份的数量就越小,也就是它的分数单位就越小。
原题说法正确。
故答案为:√。
【点评】解决本题关键是理解分数的意义和分数单位的意义。
21.、、、都能化成有限小数。 √
【答案】√
【分析】首先,要把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。
【解答】解:的分母中只含有质因数2,所以能化成有限小数;
化简后是,分母中只含有质因数5,所以能化成有限小数;
化简后是,分母中只含有质因数2,所以能化成有限小数;
的分母中只含有质因数2,所以能化成有限小数。
根据以上分析,原题干说法正确。
故答案为:√。
【点评】此题主要考查什么样的分数可以化成有限小数。注意要分数先化简。
22.如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。 √
【答案】√
【分析】用正负数表示意义相反的两种量:高于平均身高记作正,则低于平均身高就记作负。由此得解。
【解答】解:如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。原题说法正确。
故答案为:√。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
四.计算题(共3小题)
23.直接写得数。
2.4×5%= 0.25×12= 5﹣1.7= 23×498≈
73×101= 632÷69≈
【答案】0.12;3;3.3;10000;;7373;;9。
【分析】根据百分数、小数、分数和整除的乘除法的计算法则计算即可。
【解答】解:
2.4×5%=0.12 0.25×12=3 5﹣1.7=3.3 23×498≈10000
73×101=7373 632÷69≈9
【点评】解答此题要运用百分数、小数、分数和整除的乘除法的计算法则计算。
24.选择合适的方法脱式计算下列各题。
(1)750+450÷12×16 (2)99×99+99
(3)33.78+16.32+66.22﹣6.32 (4)
(5)780÷2.5÷4 (6)
【答案】(1)1350;(2)9900;(3)110;(4)0.7;(5)78;(6)。
【分析】(1)先算除法,再算乘法,最后算加法。
(2)根据乘法分配律a×(b+c)=ab+ac计算简便。
(3)根据乘法交换律和结合律计算简便。
(4)根据乘法分配律a×(b+c)=ab+ac计算简便。
(5)根据连除的性质a÷b÷c=a÷(b×c)计算简便。
(6)先算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法。
【解答】解:(1)750+450÷12×16
=750+37.5×16
=750+600
=1350
(2)99×99+99
=99×(99+1)
=99×100
=9900
(3)33.78+16.32+66.22﹣6.32
=33.78+66.22+(16.32﹣6.32)
=100+10
=110
(4)()×2.4
=0.4+0.3
=0.7
(5)780÷2.5÷4
=780÷(2.5×4)
=780÷10
=78
(6)[(0.25)]
[]
【点评】本题考查了混合运算的顺序和用简便方法计算的计算能力。
的运算定律简便计算。
五.操作题(共1小题)
25.(1)图中点A的位置是(1,4),点B的位置是 (5,4) ,点D的位置是 (2,6) 。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 (6,6) 请你在图中标示出点C并画出所围成的平行四边形。
(3)将图①先 向右平移4格 ,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。
【答案】(1)(5,4),(2,6);(2)(6,6);(3)向右平移4格;(4)。
【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,图中点A的位置是(1,4),点B的位置是 (5,4),点D的位置是 (2,6),据此解答即可。
(2)根据平行四边形的特征,要使点A、B、C、D围成的四边形是一个平行四边形,结合数对表示位置的方法可知,点C的位置是 (6,6),在图中标示出点C并画出所围成的平行四边形即可。
(3)根据平移的方法可知,将图①先向右平移4格,再向下平移3格得到图②,据此解答即可。
(4)根据旋转的方法,点O不动,画出图①绕点O逆时针旋转90°后的图形即可。
【解答】解:(1)图中点A的位置是(1,4),点B的位置是 (5,4),点D的位置是 (2,6)。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 (6,6),在图中标示出点C并画出所围成的平行四边形。如图:
(3)将图①先向右平移4格,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。如图:
故答案为:(5,4),(2,6);(6,6);向右平移4格。
【点评】本题考查了数对表示位置、平移、旋转以及平行四边形的特征等知识,结合题意分析解答即可。
六.应用题(共5小题)
26.如表是某年两年期整存整取存款年利率调整情况统计表。
日期 3月1日 5月11日 6月28日 8月26日 10月24日
利率(%) 3.10 2.85 2.60 2.35 2.10
(1)该年的两年期存款利率呈 下降 趋势,折线统计图能清晰地反映出利率的 变化 。
(2)王奶奶在该年6月28日将5000元以整存整取形式存入银行,存期两年,到期时王奶奶连本带息一共可以拿到多少钱?
【答案】(1)下降;变化。
(2)5260元。
【分析】(1)由图可知,该年的两年期存款利率呈下降趋势,折线统计图能清晰地反映出利率的变化。
(2)该年6月28日整存整取的利率为2.60%,然后根据“本金×利率×时间+本金=本息共多少元”,运用公式解答即可。
【解答】解:(1)该年的两年期存款利率呈下降趋势,折线统计图能清晰地反映出利率的变化。
(2)5000×2.60%×2+5000
=130×2+5000
=260+5000
=5260(元)
答:到期时王奶奶连本带息一共可以拿到5260元。
故答案为:下降;变化。
【点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应),本息=本金+利息,找清数据与问题,代入公式计算即可。
27.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92厘米,传统的丝绸之路实际全长约为多少千米?
【答案】6440千米。
【分析】根据图上距离÷比例尺=实际距离,用92即可求出传统的丝绸之路的实际距离,再把结果换算成千米作单位,据此解答。
【解答】解:92
=92×7000000
=644000000(厘米)
644000000厘米=6440千米
答:传统的丝绸之路实际全长约为6440千米。
【点评】解答此题的主要依据是:图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
28.一个养殖场,养鸡2500只,养鸭的只数比鸡的只数多。养殖场养鸭多少只?
【答案】4000只。
【分析】把养殖场养鸡的只数看作单位“1”,则养鸭的只数是鸡的(1),根据分数乘法的意义,即可计算出养殖场养鸭多少只。
【解答】解:
=2500×1.6
=4000(只)
答:养殖场养鸭4000只。
【点评】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
29.一个圆柱形饼干盒,底面直径是2分米,高是35厘米,要在它的四周贴一圈包装纸(接头处1厘米)。求包装纸的面积。
【答案】223.3平方厘米。
【分析】圆柱形饼干盒的侧面展开式长方形,长是底面圆的周长加1厘米,宽是35厘米。长方形面积=长×宽。
【解答】解:2分米=20厘米
(20×π+1)×35
=63.8×35
=223.3(平方厘米)
答:包装纸的面积是223.3平方厘米。
【点评】熟悉圆柱侧面积的计算公式是解决本题的关键。
30.一个圆锥形小麦堆,底面周长是18.84米,高2米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
【答案】14.13吨。
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出这堆小麦的体积,然后用这堆小麦的体积乘每立方米小麦的质量即可。
【解答】解:750千克=0.75吨
3.14×(18.84÷3.14÷2)2×2×0.75
3.14×9×2×0.75
=18.84×0.75
=14.13(吨)
答:这堆小麦大约重14.13吨。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.有两件衣服进价相同,一件比进价高15%出售,另一件打八五折出售,那么商场( )
A.赚了 B.赔了
C.不赚也不赔
2.下面两种量成反比例的是( )
A.圆的半径和面积
B.路程一定,平均速度和时间
C.书的单价一定,买的本数和所付书费
3.如图为一张长方形纸折起来以后的图形,其中∠1=30°,∠2是( )°。
A.30 B.150 C.75
4.一个晴朗的下午,奇奇站在一棵树旁拍照。奇奇的身高是1.5米,他在阳光下的影子长2.5米。此时树的影子比奇奇的影子长5米,这棵树的实际高度约是( )米。
A.3米 B.3.5米 C.4米 D.4.5米
5.下列说法中错误的是( )
A.医生记录病人的体温变化情况选用折线统计图比较合适。
B.1.8是3的倍数,3是1.8的因数。
C.一个三角形三个内角度数的比是5:3:4,这是一个锐角三角形。
D.一个正方形的边长是非0的自然数,它的周长一定是偶数。
6.下面的图形中,( )是正方体的展开图。
A. B. C.
7.下面各图中,能说明乘法分配律的是( )
A.
B.
C.
D.
二.填空题(共10小题)
8.如果甲=2×2×3,乙=2×3×5,那么甲、乙两数的最大公因数是 ,最小公倍数 。
9.一根电线长24m,用去它的,求还剩多少米.列式为 。
10.一个数的最大因数是18,这个数的最小因数是 ,这个数的最小倍数是 。
11.一个三位小数,精确到百分位约是1.88,这个三位小数最小是 ,最大是 。
12.梧桐郡小区为增加小区的绿化率,新铺了一块草坪,形状是平行四边形,如图,这个平行四边形的面积是 平方米。与这个平行四边形等底等高的三角形的面积是 平方米。
13.如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= cm。
14.要使□56÷38的商是两位数,□里最小可以填 ;
要使619÷□7的商是一位数,□里最小可以填 。
15.如图是我国未成年人图书阅读量统计图。2021年,我国 周岁的图书的阅读量最大。与2020相比,2021年 周岁的阅读量增加最多。
16.如图是用型号相同的灰、白两种三角形瓷砖铺成的图形。仔细观察,按这样的规律铺下去,第6幅图铺灰、白瓷砖一共 块,第n幅图铺灰、白瓷砖一共 块。
17.1700cm3= dm3
45分= 时
5.26L= L mL
三.判断题(共5小题)
18.如图折叠成正方体后,与a相对的面上的数字是2。
19.六年级的34位同学中,至少有3位同学在同一个月过生日。
20.分数的分母越大,它的分数单位就越小。
21.、、、都能化成有限小数。
22.如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。
四.计算题(共2小题)
23.直接写得数。
2.4×5%= 0.25×12= 5﹣1.7= 23×498≈
73×101= 632÷69≈
24.选择合适的方法脱式计算下列各题。
(1)750+450÷12×16 (2)99×99+99
(3)33.78+16.32+66.22﹣6.32 (4)
(5)780÷2.5÷4 (6)
五.操作题(共1小题)
25.(1)图中点A的位置是(1,4),点B的位置是 ,点D的位置是 。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 请你在图中标示出点C并画出所围成的平行四边形。
(3)将图①先 ,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。
六.应用题(共5小题)
26.如表是某年两年期整存整取存款年利率调整情况统计表。
日期 3月1日 5月11日 6月28日 8月26日 10月24日
利率(%) 3.10 2.85 2.60 2.35 2.10
(1)该年的两年期存款利率呈 趋势,折线统计图能清晰地反映出利率的 。
(2)王奶奶在该年6月28日将5000元以整存整取形式存入银行,存期两年,到期时王奶奶连本带息一共可以拿到多少钱?
27.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92厘米,传统的丝绸之路实际全长约为多少千米?
28.一个养殖场,养鸡2500只,养鸭的只数比鸡的只数多。养殖场养鸭多少只?
29.一个圆柱形饼干盒,底面直径是2分米,高是35厘米,要在它的四周贴一圈包装纸(接头处1厘米)。求包装纸的面积。
30.一个圆锥形小麦堆,底面周长是18.84米,高2米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
2024-2025学年六年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
1.有两件衣服进价相同,一件比进价高15%出售,另一件打八五折出售,那么商场( )
A.赚了 B.赔了
C.不赚也不赔
【答案】C
【分析】假设这两件衣服的价钱均为100元,分别计算出利润和赔钱数,再进行比较,即可解答。
【解答】解:假设这两件衣服的价钱均为100元;
100×15%=15(元)
八五折出售即为进价的85%出售。
100×(1﹣85%)
=100×15%
=15(元)
15=15
答:商场不赚也不赔。
故选:C。
【点评】本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。
2.下面两种量成反比例的是( )
A.圆的半径和面积
B.路程一定,平均速度和时间
C.书的单价一定,买的本数和所付书费
【答案】B
【分析】根据各选项中两个相关联的量是乘积一定还是比值一定解答。
【解答】解:选项A中,根据S=πr2,所以圆的半径和面积不成比例。
选项B中,平均速度×时间=路程(一定),所以平均速度和时间成反比例关系。
选项C中,书费÷本数=单价(一定),所以买的本数和所付书费成正比例关系。
故选:B。
【点评】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
3.如图为一张长方形纸折起来以后的图形,其中∠1=30°,∠2是( )°。
A.30 B.150 C.75
【答案】C
【分析】如图,∠1+∠2+∠3=180°,由∠1=30°,得出∠2+∠3=150°,由对折的性质可知∠3=∠2,进一步求得∠2即可。
【解答】解:如图:
由对折的性质可知∠3=∠2,因为,∠1+∠2+∠3=180°,∠1=30°,所以∠2+∠3=150°,∠2=150°÷2=75°。
答:∠2是75°。
故选:C。
【点评】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题,结合题意分析解答即可。
4.一个晴朗的下午,奇奇站在一棵树旁拍照。奇奇的身高是1.5米,他在阳光下的影子长2.5米。此时树的影子比奇奇的影子长5米,这棵树的实际高度约是( )米。
A.3米 B.3.5米 C.4米 D.4.5米
【答案】D
【分析】依据题意可知,身高与影子的长度成正比例,由此列式计算即可。
【解答】解:(2.5+5)×1.5÷2.5
=7.5×1.5÷2.5
=4.5(米)
答:这棵树的实际高度约4.5米。
故选:D。
【点评】本题考查的是正比例的应用。
5.下列说法中错误的是( )
A.医生记录病人的体温变化情况选用折线统计图比较合适。
B.1.8是3的倍数,3是1.8的因数。
C.一个三角形三个内角度数的比是5:3:4,这是一个锐角三角形。
D.一个正方形的边长是非0的自然数,它的周长一定是偶数。
【答案】B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此判断即可。
倍数、因数是针对整数来说的,据此判断即可;
三角形的内角和是180度,又知三个内角的度数的比,运用按比例分配方法求出最大角的度数并判定三角形的类型即可;
根据偶数的意义,假设正方形的边长是n(n是非零自然数),它的周长是4n,4n一定是偶数,由此判断即可。
【解答】解:A.医生记录病人的体温变化情况选用折线统计图比较合适。故原题说法正确;
B.倍数、因数是针对整数来说的,故原题说法错误;
C.180°75°,因为最大的内角是70°,所以这个三角形是锐角三角形,故原题说法正确;
D.边长是非零自然数的正方形,它的周长一定是偶数。所以原题说法正确。
故选:B。
【点评】本题主要考查了统计图的选择、倍数及因数、偶数和三角形内角和及三角形类型的判断。
6.下面的图形中,( )是正方体的展开图。
A. B. C.
【答案】A
【分析】A.展开图符合正方体展开图“一四一”型;B.C.展开图中出现了“田”字型;根据正方体展开图的特征解答。
【解答】解:A.展开图符合正方体展开图“一四一”型,是正方体的展开图;
B.C.展开图中出现了“田”字型,不是正方体的展开图。
故选:A。
【点评】本题考查正方体的展开图,掌握正方体展开图的特征是解题的关键。
7.下面各图中,能说明乘法分配律的是( )
A.
B.
C.
D.
【答案】D
【分析】根据乘法分配律的意义,两个数的和与一个数相乘,可以把这两个加数分别与这个数相乘,然后把两个积相加,结果不变,这叫做乘法分配律;两个数相加,交换加数的位置,和不变;三个数相加,可以先把前两个数相加,也可以把后两个数相加;据此进行分析解答即可。
【解答】解:A.运用加法交换律进行计算,不符合题意;
B.没有运用运算定律,不符合题意;
C.运用加法交换律和结合律进行计算,不符合题意;
D.运用乘法分配律进行计算,符合题意;
故选:D。
【点评】此题考查的目的是理解掌握乘法分配律、加法交换和加法结合律的意义及应用。
二.填空题(共10小题)
8.如果甲=2×2×3,乙=2×3×5,那么甲、乙两数的最大公因数是 6 ,最小公倍数 60 。
【答案】6;60。
【分析】先把要求的两个数分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:因为甲=2×2×3,乙=2×3×5,所以甲、乙两数的最大公因数是2×3=6,最小公倍数2×2×3×5=60。
故答案为:6;60。
【点评】考查了求几个数的最大公因数的方法与最小公倍数的方法:两个数的公有质因数连乘积是最大公因数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数。
9.一根电线长24m,用去它的,求还剩多少米.列式为 24×(1) 。
【答案】24×(1)。
【分析】把这根电线的全长看成单位“1”,用去它的,还剩下全长的1,用全长乘上这个分率就是剩下的长度。
【解答】解:1
列式为:24×(1)
故答案为:24×(1)。
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法。
10.一个数的最大因数是18,这个数的最小因数是 1 ,这个数的最小倍数是 18 。
【答案】1;18。
【分析】一个数的最大因数是它本身,最小因数是1;一个数的最小倍数是它本身。一个数的最大因数是18,所以这个数是18。
【解答】解:一个数的最大因数是18,这个数的最小因数是1,这个数的最小倍数是18。
故答案为:1;18。
【点评】本题考查了找一个数的因数、倍数。
11.一个三位小数,精确到百分位约是1.88,这个三位小数最小是 1.875 ,最大是 1.884 。
【答案】1.875,1.884。
【分析】要考虑1.88是一个三位小数的近似数,有两种情况:“五入”得到的1.88最小是1.875,“四舍”得到的1.88最大是1.884,由此解答问题即可。
【解答】解:一个三位小数,精确到百分位约是1.88,这个三位小数最小是1.875,最大是1.884。
故答案为:1.875,1.884。
【点评】取一个小数的近似数,有两种情况:“四舍”得到的近似数比原数小,“五入”得到的近似数比原数大,根据题的要求灵活掌握解答方法。
12.梧桐郡小区为增加小区的绿化率,新铺了一块草坪,形状是平行四边形,如图,这个平行四边形的面积是 270 平方米。与这个平行四边形等底等高的三角形的面积是 135 平方米。
【答案】270;135。
【分析】根据平行四边形的面积公式计算,平行四边形的面积=底×高;与这个平行四边形等底等高的三角形的面积是这个平行四边形面积的一半,据此解答即可。
【解答】解:18×15=270(平方米)
270÷2=135(平方米)
答:这个平行四边形的面积是270平方米。与这个平行四边形等底等高的三角形的面积是135平方米。
故答案为:270;135。
【点评】熟练掌握平行四边形的面积和三角形的面积公式,是解答本题的关键。
13.如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= 5 cm。
【答案】5。
【分析】读题发现:已知三角形ABC的三条边的长度,按比例算出CE长度即可。
【解答】解:设CE的长度为xcm,则:
8:(12﹣8)=10:x
8:4=10:x
8x=4×10
8x=40
8x÷8=40÷8
x=5
故答案为:5。
【点评】本题考查了图形的放大、比的意义的应用问题,解答本题的关键或突破口在于清楚:AB与BD的长度比等于AC与CE的长度比,据此写出比例再算出结果即可。
14.要使□56÷38的商是两位数,□里最小可以填 4 ;
要使619÷□7的商是一位数,□里最小可以填 6 。
【答案】4;6。
【分析】□56÷38要使商是两位数,被除数前两位数大于或等于除数38;要使619÷□7的商是一位数,被除数前两位数小于除数,然后再进一步解答。
【解答】解:要使□56÷38的商是两位数,□5≥38,□里可以填4,5,6,7,8,9,□里最小可以填4;
要使619÷□7的商是一位数,61<□7,□里可以填6,7,8,9,□里最小可以填6。
故答案为:4;6。
【点评】本题考查除数是两位数的除法的计算及应用。注意计算的准确性。
15.如图是我国未成年人图书阅读量统计图。2021年,我国 14~17 周岁的图书的阅读量最大。与2020相比,2021年 9~13 周岁的阅读量增加最多。
【答案】14~17,9~13。
【分析】从条形统计图可看出,14~17周岁的条形最高,空白和阴影条形相差最多的是9~13周岁。
【解答】解:10.21<10.33<13.1
9.63<10.02<13.07
10.21﹣9.63=0.58
10.33﹣10.02=0.31
13.1﹣13.07=0.03
0.03<0.31<0.58
故答案为:14~17,9~13。
【点评】本题考查了学生从统计图中获取信息的意识。
16.如图是用型号相同的灰、白两种三角形瓷砖铺成的图形。仔细观察,按这样的规律铺下去,第6幅图铺灰、白瓷砖一共 49 块,第n幅图铺灰、白瓷砖一共 (n+1)2 块。
【答案】49,(n+1)2。
【分析】根据观察,图中三角形瓷砖的个数分别是4、9、16……,4=22;9=32;16=42;……由此即可得出第n个图形铺瓷砖的总块数为(n+1)2块。
【解答】解:根据题干得出图中三角形瓷砖的个数分别是4=22;9=32;16=42;……则第n个图形铺瓷砖的总块数为(n+1)2块;
(6+1)2=49(个)
第6幅图铺灰、白瓷砖一共49块,第n幅图铺灰、白瓷砖一共(n+1)2块。
故答案为:49,(n+1)2。
【点评】由题干中的图形的排列以及个数特点,得出瓷砖的排列规律是解决此类问题的关键。
17.1700cm3= 1.7 dm3
45分= 0.75 时
5.26L= 5 L 260 mL
【答案】1.7;0.75;5;260。
【分析】根据1立方分米=1000立方厘米,1小时=60分,1升=1000毫升,解答此题即可。
【解答】解:1700cm3=1.7dm3
45分=0.75时
5.26L=5L260mL
故答案为:1.7;0.75;5;260。
【点评】熟练掌握体积单位、时间单位、锐角单位的换算,是解答此题的关键。
三.判断题(共5小题)
18.如图折叠成正方体后,与a相对的面上的数字是2。 ×
【答案】×
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣3﹣2”型,折叠成正方体后,数字1与字母a相对,2与4相对,3与5相对。
【解答】解:如图:
折叠成正方体后,与a相对的面上的数字是1。
原题说法错误。
故答案为:×。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
19.六年级的34位同学中,至少有3位同学在同一个月过生日。 √
【答案】√
【分析】一年有12个月,把12个月看作12个抽屉,34位同学看作物体个数,根据抽屉原理得:34÷12=2……10;则至少有:2+1=3(位)在同一个月过生日。
【解答】解:建立抽屉:一年有12个月分别看做12个抽屉,
34÷12=2(位)……10(位)
2+1=3(位)
答:至少有3位同学在同一个月过生日。
故答案为:√。
【点评】此题属于典型的抽屉原理习题,解答此类题的关键是找出把谁看作“抽屉个数”,把谁看作“物体个数”,然后根据抽屉原理解答即可。
20.分数的分母越大,它的分数单位就越小。 √
【答案】√
【分析】把一个整体平均分成若干份,其中的1份就是几分之一,也就是这个分数的分数单位,平均分的份数越多,它的分母就越大,每份的数量就越小,也就是份数单位就越小,由此判断。
【解答】解:分数的分母越大,每份的数量就越小,也就是它的分数单位就越小。
原题说法正确。
故答案为:√。
【点评】解决本题关键是理解分数的意义和分数单位的意义。
21.、、、都能化成有限小数。 √
【答案】√
【分析】首先,要把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。
【解答】解:的分母中只含有质因数2,所以能化成有限小数;
化简后是,分母中只含有质因数5,所以能化成有限小数;
化简后是,分母中只含有质因数2,所以能化成有限小数;
的分母中只含有质因数2,所以能化成有限小数。
根据以上分析,原题干说法正确。
故答案为:√。
【点评】此题主要考查什么样的分数可以化成有限小数。注意要分数先化简。
22.如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。 √
【答案】√
【分析】用正负数表示意义相反的两种量:高于平均身高记作正,则低于平均身高就记作负。由此得解。
【解答】解:如果“+6cm”表示比平均身高高6cm,那么“﹣3cm”表示比平均身高矮3cm。原题说法正确。
故答案为:√。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
四.计算题(共3小题)
23.直接写得数。
2.4×5%= 0.25×12= 5﹣1.7= 23×498≈
73×101= 632÷69≈
【答案】0.12;3;3.3;10000;;7373;;9。
【分析】根据百分数、小数、分数和整除的乘除法的计算法则计算即可。
【解答】解:
2.4×5%=0.12 0.25×12=3 5﹣1.7=3.3 23×498≈10000
73×101=7373 632÷69≈9
【点评】解答此题要运用百分数、小数、分数和整除的乘除法的计算法则计算。
24.选择合适的方法脱式计算下列各题。
(1)750+450÷12×16 (2)99×99+99
(3)33.78+16.32+66.22﹣6.32 (4)
(5)780÷2.5÷4 (6)
【答案】(1)1350;(2)9900;(3)110;(4)0.7;(5)78;(6)。
【分析】(1)先算除法,再算乘法,最后算加法。
(2)根据乘法分配律a×(b+c)=ab+ac计算简便。
(3)根据乘法交换律和结合律计算简便。
(4)根据乘法分配律a×(b+c)=ab+ac计算简便。
(5)根据连除的性质a÷b÷c=a÷(b×c)计算简便。
(6)先算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法。
【解答】解:(1)750+450÷12×16
=750+37.5×16
=750+600
=1350
(2)99×99+99
=99×(99+1)
=99×100
=9900
(3)33.78+16.32+66.22﹣6.32
=33.78+66.22+(16.32﹣6.32)
=100+10
=110
(4)()×2.4
=0.4+0.3
=0.7
(5)780÷2.5÷4
=780÷(2.5×4)
=780÷10
=78
(6)[(0.25)]
[]
【点评】本题考查了混合运算的顺序和用简便方法计算的计算能力。
的运算定律简便计算。
五.操作题(共1小题)
25.(1)图中点A的位置是(1,4),点B的位置是 (5,4) ,点D的位置是 (2,6) 。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 (6,6) 请你在图中标示出点C并画出所围成的平行四边形。
(3)将图①先 向右平移4格 ,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。
【答案】(1)(5,4),(2,6);(2)(6,6);(3)向右平移4格;(4)。
【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,图中点A的位置是(1,4),点B的位置是 (5,4),点D的位置是 (2,6),据此解答即可。
(2)根据平行四边形的特征,要使点A、B、C、D围成的四边形是一个平行四边形,结合数对表示位置的方法可知,点C的位置是 (6,6),在图中标示出点C并画出所围成的平行四边形即可。
(3)根据平移的方法可知,将图①先向右平移4格,再向下平移3格得到图②,据此解答即可。
(4)根据旋转的方法,点O不动,画出图①绕点O逆时针旋转90°后的图形即可。
【解答】解:(1)图中点A的位置是(1,4),点B的位置是 (5,4),点D的位置是 (2,6)。
(2)要使点A、B、C、D围成的四边形是一个平行四边形,点C的位置是 (6,6),在图中标示出点C并画出所围成的平行四边形。如图:
(3)将图①先向右平移4格,再向下平移3格得到图②。
(4)画出图①绕点O逆时针旋转90°后的图形。如图:
故答案为:(5,4),(2,6);(6,6);向右平移4格。
【点评】本题考查了数对表示位置、平移、旋转以及平行四边形的特征等知识,结合题意分析解答即可。
六.应用题(共5小题)
26.如表是某年两年期整存整取存款年利率调整情况统计表。
日期 3月1日 5月11日 6月28日 8月26日 10月24日
利率(%) 3.10 2.85 2.60 2.35 2.10
(1)该年的两年期存款利率呈 下降 趋势,折线统计图能清晰地反映出利率的 变化 。
(2)王奶奶在该年6月28日将5000元以整存整取形式存入银行,存期两年,到期时王奶奶连本带息一共可以拿到多少钱?
【答案】(1)下降;变化。
(2)5260元。
【分析】(1)由图可知,该年的两年期存款利率呈下降趋势,折线统计图能清晰地反映出利率的变化。
(2)该年6月28日整存整取的利率为2.60%,然后根据“本金×利率×时间+本金=本息共多少元”,运用公式解答即可。
【解答】解:(1)该年的两年期存款利率呈下降趋势,折线统计图能清晰地反映出利率的变化。
(2)5000×2.60%×2+5000
=130×2+5000
=260+5000
=5260(元)
答:到期时王奶奶连本带息一共可以拿到5260元。
故答案为:下降;变化。
【点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应),本息=本金+利息,找清数据与问题,代入公式计算即可。
27.“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1:7000000的地图上约长92厘米,传统的丝绸之路实际全长约为多少千米?
【答案】6440千米。
【分析】根据图上距离÷比例尺=实际距离,用92即可求出传统的丝绸之路的实际距离,再把结果换算成千米作单位,据此解答。
【解答】解:92
=92×7000000
=644000000(厘米)
644000000厘米=6440千米
答:传统的丝绸之路实际全长约为6440千米。
【点评】解答此题的主要依据是:图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
28.一个养殖场,养鸡2500只,养鸭的只数比鸡的只数多。养殖场养鸭多少只?
【答案】4000只。
【分析】把养殖场养鸡的只数看作单位“1”,则养鸭的只数是鸡的(1),根据分数乘法的意义,即可计算出养殖场养鸭多少只。
【解答】解:
=2500×1.6
=4000(只)
答:养殖场养鸭4000只。
【点评】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
29.一个圆柱形饼干盒,底面直径是2分米,高是35厘米,要在它的四周贴一圈包装纸(接头处1厘米)。求包装纸的面积。
【答案】223.3平方厘米。
【分析】圆柱形饼干盒的侧面展开式长方形,长是底面圆的周长加1厘米,宽是35厘米。长方形面积=长×宽。
【解答】解:2分米=20厘米
(20×π+1)×35
=63.8×35
=223.3(平方厘米)
答:包装纸的面积是223.3平方厘米。
【点评】熟悉圆柱侧面积的计算公式是解决本题的关键。
30.一个圆锥形小麦堆,底面周长是18.84米,高2米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
【答案】14.13吨。
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出这堆小麦的体积,然后用这堆小麦的体积乘每立方米小麦的质量即可。
【解答】解:750千克=0.75吨
3.14×(18.84÷3.14÷2)2×2×0.75
3.14×9×2×0.75
=18.84×0.75
=14.13(吨)
答:这堆小麦大约重14.13吨。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
