(期末提分卷)期末核心考点突破提分卷-2024-2025学年五年级下学期数学北师大版(含解析)
文档属性
| 名称 | (期末提分卷)期末核心考点突破提分卷-2024-2025学年五年级下学期数学北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 192.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 11:31:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心考点突破提分卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、填空题
1.甲、乙两人加工同一种零件,甲加工的零件个数比乙少20%,乙加工的时间比甲少,则乙的工作效率是甲的 %。
2.制作一个棱长为5dm的无盖正方体鱼缸,至少需要 dm2玻璃,可以装 dm3的水。
3.一个长方体的长是5dm,宽4dm,高是2.5dm,它的体积是 dm 。
4.已知 %(M、N、L 均不为0),则M、N、L 这三个数的大小关系是 。
5.学校运动会,参赛运动员在170~180人之间,女运动员人数是男运动员人数的 。女运动员有 人。
6. 一个长方体有两个相对的面是正方形,这个长方体最多有 条棱的长度相等。用12根小棒拼搭只有四个面都是正方形的长方体,肯定 成功。(括号里填“能”或“不能”)
7.2020年盐城成功入选第六届全国文明城市,为此,小娟同学特制一个正方体玩具,展开图如图所示,则原正方体中与“全”字所在面相对的面上的字是 。
8.如图,几个棱长是1分米的正方体堆放在墙角,露在外面的面积是 平方分米,体积一共是 立方分米.
9.李大爷用一批化肥给承包的麦田施肥。若每亩施6千克,则缺少化肥300千克;若每亩施5千克,则余下化肥200千克。那么李大爷共承包了麦田 亩,这批化肥有 千克。
10. =4÷5= = ÷15= (填小数)
11.比较下面数的大小。
0.13
12.一个正方体的 6 个面上分别写着 这 6 个字母,右图是这个正方体的不同摆放, 的对面是
13.一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是 立方厘米。
14.一杯牛奶李明分三次喝,第一次喝了 ,然后加满水;第二次喝了 ,然后再加满水;第三次一饮而尽,李明喝了 杯牛奶, 杯水。
二、判断题
15.甲数是10的 ,乙数的 是6,丙数是6个 ,则乙数>丙数>甲数.( )
16. 12× 和 ×12的意义相同。( )
17.从里连续减去4个 后是 。( )
18.1号点在2号点的南偏西40°方向上,那么2号点在1号点的北偏东40°方向上。( )
19.如果ab≠0,且a20.正方体与长方体都可以用“底面积×高”求体积。( )
21.两个分数的积一定比这两个分数大。( )
22.用4个同样大小的小正方体能拼成一个大正方体。( )
23.面积单位比长度单位大。( )
三、单选题
24.小西家在小青家东偏北30°方向900米处,则小青家在小西家( )
A.北偏东30°方向900米处 B.西偏南60°方向900米处
C.东偏北60°方向900米处 D.南偏西60°方向900米处
25.一个棱长是4分米的正方体,棱长总和是( )分米。
A.24 B.32 C.48
26.你自己的一只拳头慢慢地伸进装满水的脸盆中,溢出来的水的体积大约是( )
A.小于1毫升,大于1升 B.大于1立方米,小于1升
C.大于1升,小于1立方米 D.大于1毫升,小于1升
27.一根绳子,剪去 后还剩下 米.这根绳子原来长多少米 正确列式是( )。
A. + B. ÷(1- )
C. + × D. ÷
28.小明和小莉出生于2003年12月份,他们的出生日不是同一天,但是都是星期四,且小明比小莉出生早,两个人出生日期之和是22,那么小莉的出生日期是
A.15号 B.16号 C.17号 D.18号
29.林林家在邮局的南偏东40°方向上,则邮局在林林家( )方向上。
A.西偏北40° B.北偏西40° C.东偏南50°
30.把一个圆锥完全浸没在一个底面直径为6厘米的圆柱形容器里,水位上升了4厘米。这个圆锥的体积是( )立方厘米。
A. B. C. D.
31.将一个长方体的高截去5cm就变成了正方体(如图),正方体的表面积比原长方体的表面积减少了60cm2,原长方体的体积是( )立方厘米。
A.27 B.36 C.64 D.72
32.商场的自动扶梯以匀速由下往上行驶,两个孩子嫌扶梯走得太慢,于是在行驶的扶梯上,男孩每秒钟向上走2个梯级,女孩每2秒向上走3个梯级。结果男孩用40秒钟到达,女孩用50秒钟到达。则当该扶梯静止时,可看到的扶梯级有:( )
A.80级 B.100级 C.120级 D.140 级
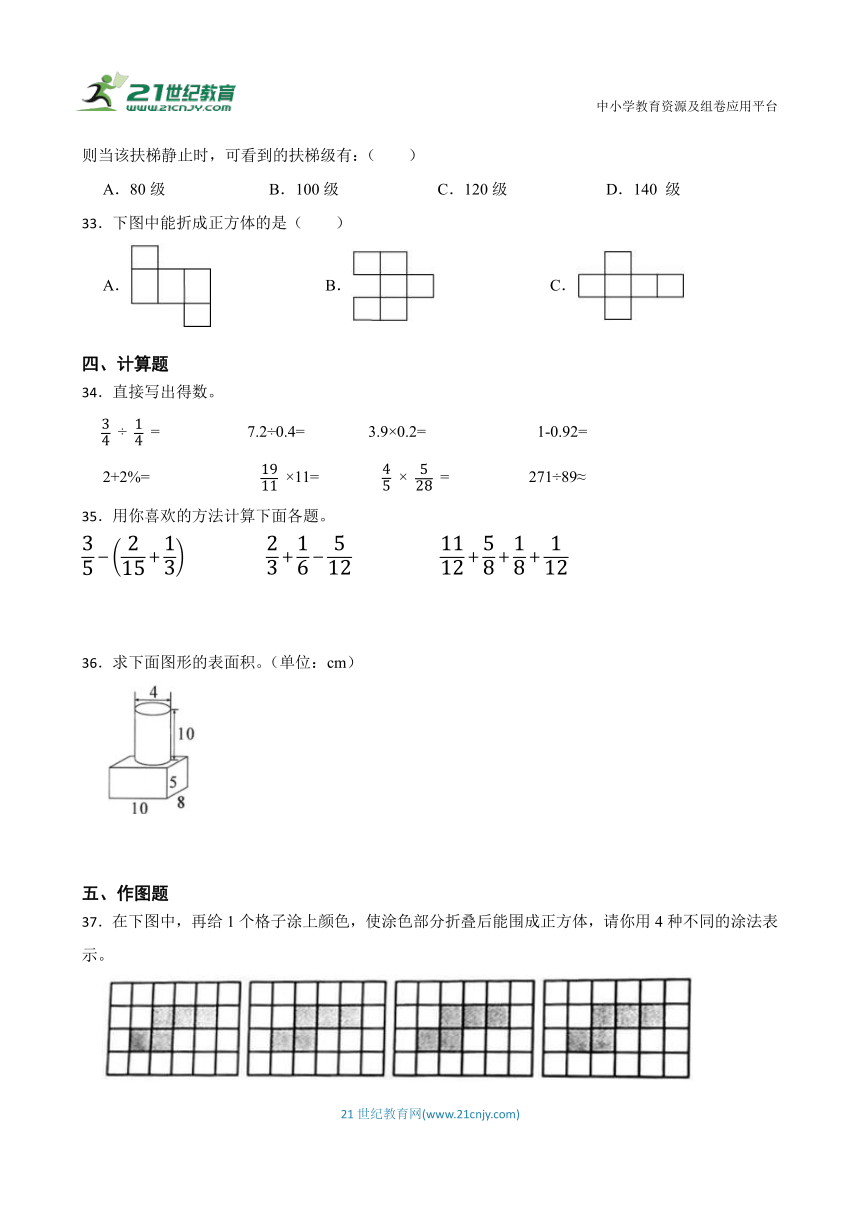
33.下图中能折成正方体的是( )
A. B. C.
四、计算题
34.直接写出得数。
÷ = 7.2÷0.4= 3.9×0.2= 1-0.92=
2+2%= ×11= × = 271÷89≈
35.用你喜欢的方法计算下面各题。
36.求下面图形的表面积。(单位:cm)
五、作图题
37.在下图中,再给1个格子涂上颜色,使涂色部分折叠后能围成正方体,请你用4种不同的涂法表示。
六、解决问题
38.“十一”期间,学校将每个教室的屋顶和四壁粉刷一新。经测量六(1)班的教室长8米,宽6米,高3.5米,(黑板和门窗共14平方米)粉刷的面积一共有多少平方米?如果每平方米使用涂料0.8千克,粉刷六(1)班的教室共使用了涂料多少千克?
39.一本练习本4.5元,比一盒水彩笔便宜10.5元,那一盒水彩笔多少元钱?(列方程解决问题)
40.甲、乙两个水管同时注两个同样大小的水池,且速度比为 7 : 5,小时之后,两个水池的水量之和刚好是一个满水池的水量 . 此时,甲水管的速度提高 25%,乙水管的速度降低,当甲水管注满水池后,乙水管还要多久才能注满水池
41.老李早上8:00从甲地出发去乙地,每小时行12千米,在乙地办事用去1.5小时,为了赶在12:00回家吃午饭,他把速度提高了,请问甲乙两地相距多少千米?
42.甲、乙两人分别从相距4900米的A、B两地出发,相向而行,甲出发10分钟后乙才出发,甲、乙的速度比为5:6甲出发50分钟后两人相遇,他们的速度各是多少?
43.一个礼盒(如下图),像这样用彩带捆扎起来,至少需要多长的彩带?(打结处需要25厘米)
44.一个长10dm,宽8dm,高7dm的长方体容器装有5dm深的水,放入一块石头完全沉入水中,水面上升到5.5dm处。这块石头的体积是多少立方分米?
45.自古至今,宣纸就是创作中国书画的最佳材料。为了迎接学校书法比赛,五年级一班买来一批宣纸供大家练习使用,第一次用去了这批宣纸的,第二次用去了这批宣纸的,还剩下这批宣纸的几分之几没有用?
46.修一条 千米长的公路,第一天修了全长的 ,第二天比第一天多修了全长的 。第二天修了全长的几分之几?还剩下全长的几分之几没有修?
47.老师为参加军训的同学安排宿舍,如果每间宿舍住8人,那么这些宿舍正好住满;如果每间宿舍住6人,那么正好缺4间宿舍。参加军训的学生一共有几人
48.惠东渔歌俗称“后船歌”,是流行于港口、巽寮、稔山、盐洲等地渔村的传统音乐,是惠州市第一个国家级“非遗”。为了让更多学生了解民间传统音乐,实验小学第二课堂开设了渔歌课,乐乐每天排练时,比莉莉每天多排练时。乐乐和莉莉每天共排练多少时?
49.李叔叔准备去外地出差,在铁路12306网站上买了一张8月10日中午12:00发车的高铁票,票价为180元,他在8月8日上午10:00接到取消出差的通知。按照规定,火车票退票需要扣除手续费,规定如下表。
距离开车时间 15天以上(不含15天) 48小时及以上,15天以内 24小时以上、48小时以内 24小时以内
退票手续费 免费 票面价的 票面价的 票面价的
(1)如果李叔叔接到取消出差的通知后立即申请退票,那么应扣多少元手续费?
(2)如果李叔叔收到取消出差通知后,过了3小时才申请退票,那么能退回多少钱?
参考答案及试题解析
1.【答案】150
【解析】解:假设乙加工的零件总数是1,甲加工的时间是1。
=
=
=
=1.5×100%
=150%
故答案为:150
【分析】根据题意,把乙加工的零件总数看作单位“1”,则甲加工的零件总数是(1-20%);把甲加工的时间看作单位“1”,则乙加工的时间是);根据“工作效率=工作总量÷工作时间”,分别求出甲乙的工作效率,用乙的工作效率÷甲的工作效率×100%即可求解。
2.【答案】125;125
【解析】解:5×5×5
=25×5
=125(dm2),
所以需要125dm2玻璃;
5×5×5
=25×5
=125(dm3),
所以可以装125dm3的水。
故答案为:125;125。
【分析】至少需要玻璃的面积=棱长×棱长×5;水的体积(容积)=棱长×棱长×棱长,代入数值计算即可。
3.【答案】50
【解析】解:5×4×2.5=50dm3,所以它的体积是50dm3。
故答案为:50。
【分析】长方体的体积=长×宽×高,据此作答即可。
4.【答案】M=N=L
【解析】解:因为 N×0.375,L×37.5%=L×0.375,所以M=N=L。
故答案为:M=N=L。
【分析】把除法转化成乘法,同时把分数、百分数都化成小数,这样就能判断三个字母表示数的大小。
5.【答案】75
【解析】女运动员:男运动员=3:4,女运动员占总人数的;
180÷7 =25(人)……5(人)
25×5= 175(人)
175×=75(人)
故答案为:75。
【分析】已知女运动员人数是男运动员人数的 ,也就是女运动员:男运动员=3:4,如果把女运动员人数看作3份,男运动员就是4份,总份数就是:3+4=7份, 女运动员占总人数的,人数在 170~180人 , 能被7整除,这个数是180÷7 =25……5,人数应该是25×5= 175人,女运动员占总人数的,用175×即可解答。
6.【答案】8;不能
【解析】解:这个长方体最多有8条棱的长度相等;用12根小棒拼搭只有四个面都是正方形的长方体,肯定不能成功。
故答案为:8;不能。
【分析】长方体有两个相对的面是正方形,每个正方形有4条棱,所以长方体最多有8条棱的长度相等;
长方体最多有2个面是正方形。
7.【答案】明
【解析】解:原正方体中与“全”字所在面相对的面上的字是明。
故答案为:明。
【分析】在正方体的展开图中,相对面的特征:“Z”字型的两端;三个正方形排成的一行的两端的正方形。
8.【答案】12;6
【解析】解:3+5+4=12(个)
12×1=12(平方分米)
1×1×1×6=6(立方分米)
故答案为:12;6.
【分析】小正方体露在外面的面分成三部分:正面、上面、侧面,分别查出这几个面是多少,再计算露在外面的面积,露在外面的面积=一个小正方形的面积×露在外面的小正方形的个数。
9.【答案】500;2700
【解析】解:设承包了麦田x亩,则化肥有6x-300千克,根据题意可得,
6x-300-5x=200
解得
x=500,
6x-300=6×500-300=2700(千克);
答:李大爷共承包了麦田500亩,这批化肥有2700千克
故答案为:500,2700
【分析】设承包了麦田x亩,则化肥有6x-300千克,根据题意可得等量关系:化肥的总千克数(6x-300千克)-麦田的亩数x5千克=200千克,由此可得方程解决问题
10.【答案】16;45;12;0.8
【解析】解:4÷5=0.8
20×0.8=16
36÷0.8=45
15×0.8=12
4÷5=0.8
20×0.8=16
36÷0.8=45
15 × 0.8=12
故答案为:16,45,12,0.8
【分析】分数的分子和分母可以看作是除法的被除数和除数,分数的值就是除法的商。同时,分数的值也可以转换为小数,即分子除以分母。
11.【答案】>;<;=;>
【解析】>;<;0.13=;>=。
故答案为:>;<;=;>。
【分析】同分母相同,分子大的分数大;分子相同,分母大的分数反而小。
异分母分数比较大小,先通分将分数化成同分母分数,再比较大小。
小数与分数比较大小,先将小数化成分数,再比较大小。
小数化分数的方法:①原来有几位小数,就在1 后面写几个零作分母,②原来的小数去掉小数点作分子。注意:化成分数后,能约分的要约分。
12.【答案】D
【解析】由图2和图3可以看出,与D相邻的四个面分别是E、F、B、C,因此A的对面是D。
故答案为:D
【分析】要找出A的对面,可先确定与A相邻的四个面,与A不相邻的面即为它的对面。
13.【答案】54
【解析】解:依题意,这个长方体的长、宽、高之和是 (厘米),
于是它的宽与高都等于 (厘米),
它的长是(厘米)。
所以这个 长方体的各条棱长的和是48厘米 是 (立方厘米)。
故答案为:54
【分析】 根据“长是宽的2倍,高与宽相等”,可以把宽和高看成1份,则长为2份, 再根据长方体的各条棱长的和是48厘米,可以求出长方体的长宽高,最后根据 长方体的体积等于长乘宽乘高计算即可。
14.【答案】1;
【解析】解:李明喝了1杯牛奶;+=。
故答案为:1;。
【分析】第三次一饮而尽,说明李明把牛奶全部喝完,即喝了1杯牛奶;喝水的分率=第一次喝的分率+第二次喝的分率。
15.【答案】错误
【解析】解:甲数:10×=6,乙数:6÷=10,丙数=6×=4,4<6<10,所以乙数>甲数>丙数。
故答案为:错误。
【分析】一个数的几分之几是另一个数,那么另一个数=这个数×几分之几,这个数=另一个数÷几分之几;求几个相同加数的和,用这个相同加数×相同加数的个数。最后把三个数进行比较即可。
16.【答案】错误
【解析】12× 表示求12的 是多少, ×12表示求 的12倍是多少,因此原题说法错误。
故答案为:错误
【分析】12× 表示求12的 是多少, ×12表示求 的12倍是多少,因此12× 和 ×12的意义相同的说法错误,即可解答。
17.【答案】正确
【解析】
=
=
故答案:正确
【分析】按题目中的条件列出算式后,应先算乘法,再算减法,结果是,所以答案正确。在分数混合运算中要先算乘除法,再算加减法,最后就可以求出结果。
18.【答案】正确
【解析】解:2号点在1号点的北偏东40°方向上。说法正确。
故答案为:正确。
【分析】甲在乙什么方向和乙在甲什么方向,这两个方向相反,度数和距离不变,据此解答。
19.【答案】正确
【解析】解:a,所以6÷<6÷。
故答案为:正确。
【分析】在除法计算中,被除数不变,除数越大,商越小。
20.【答案】正确
【解析】正方体和长方体都可以用底面积乘相应的高求它的体积来进行计算,这种说法是正确的。故答案为:正确。
【分析】根据长方体与正方体的体积定义可知:正方体与长方体都可以用“底面积×高”求体积。对的。因为正方体的体积V=a×a×a,其中a×a可以看作是正方体的底面积;长方体的体积V=a×b×h,其中a×b是长方体的底面积,所以正方体和长方体的体积都可以用底面积乘高来计算。考察了正方体和长方体的体积公式。
21.【答案】错误
【解析】两个分数的积可能比这两个分数大。
故答案为:错误。
【分析】一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小,据此进行判断。
22.【答案】错误
【解析】2×2×2=8,小正方体拼大正方体,最少需要8个,本题错。
故答案为:错误。
【分析】大正方体最小时,一边有两个正方体,一共需要8个正方体。
23.【答案】错误
【解析】错误。体积单位、面积单位、长度不是同一类单位,不能比较大小
【分析】
体积单位、面积单位、长度不是同一类单位,不能比较大小,据此判断.解答本题关键是明白:只有同一类单位,才能比较大小.
24.【答案】D
【解析】解:小西家在小青家东偏北30°方向900米处,则小青家在小西家西偏南30°方向900米处或者南偏西60°方向900米处。
故答案为:D。
【分析】观察的中心相反,如果度数不变,那么方向刚好相反,也可以通过画图帮助理解方向。
25.【答案】C
【解析】4×12=48(分米)
【分析】正方体总共有12条棱,并且每条棱的长度都是一样,所以知道了每条棱的长度,就用4分米乘以12即可。
26.【答案】D
【解析】解:1立方米>1升>1毫升,
A、B描述错误,C不合适,单位过大,
故选:D。
【分析】溢出的水的体积等于拳头的体积,一个人一只拳头的体积大于1毫升,小于1升。
27.【答案】B
【解析】
故答案为:B。
【分析】把一根绳子看作单位“1”,数量之间存在以下相等关系:绳子原来的长度×(1-)=剩下绳子长度。
28.【答案】D
【解析】解:设小明的出生日期为x,那么小莉的出生日期就是x+7、x+14、x+21等,
如果他们相差7天,那么我们可以列出等式x+(x+7)=22,解出x=7.5,这不符合实际情况,所以我们舍去这种情况.
如果他们相差14天,那么我们可以列出等式x+(x+14)=22,解出x=4,这时符合题意,那么小莉的出生日期就是x+14=4+14=18.
如果他们相差21天,那么我们可以列出等式x+(x+21)=22,解出x=0.5,这不符合实际情况,所以我们舍去这种情况.
因此,小莉的出生日期应该是18号.
故答案为:D。
【分析】设小明的出生日期为x,那么小莉的出生日期就是x+7、x+14、x+21等,我们需要找到符合所有条件的解。
29.【答案】B
【解析】解:林林家在邮局的南偏东40°方向上,则邮局在林林家北偏西40°方向上。
故答案为:B。
【分析】如图:邮局在林林家北偏西40°方向或西偏北50°方向。
30.【答案】A
31.【答案】D
32.【答案】B
【解析】解:设电梯匀速时的速度为x,
(x+)×50=(x+2)×40
50x+75=40x+80
50x-40x=80-75
10x=5
x=0.5
扶梯静止时可看到的扶梯级数:(2+0.5)×40=100。
故答案为:B。
【分析】这是一个典型的行程问题的变型,总路程为“扶梯静止时可看到的扶梯级”,速度为“男孩或女孩每个单位向上运动的级数”。先列方程求出电梯匀速时的速度,然后求出扶梯静止时可看到扶梯的级数即可。
33.【答案】C
【解析】解:根据正方体展开图的11种特征,选项A、选项B不能折成正方体;选项C能折成正方形.
故选:C.
【分析】根据正方体展开图的11种特征,选项A中有长方形,不属于正方体展开图(它是长方体展开图),不能折成正方体;选项B不属于正方体展开图,不能折成正方体;选项C都属于正方体展开图的“1﹣4﹣1”型,能折成正方形.
34.【答案】 ÷ =3 7.2÷0.4=18 3.9×0.2=0.78 1-0.92=0.08
2+2%=2.02 ×11=19 × = 271÷89≈3
【解析】分数与分数相乘,分子乘以分子作为积的分子,分母乘以分母作为积的分母;
一个数除以分数等于这个数乘以这个分数的倒数;
小数乘法按照整数乘法法则计算,最后看因数中一共有几位小数,就在积的末尾查出几位小数点上小数点,小数位数不够时,在积的前面用0补齐。
小数除法,根据除法的性质将除数化成整数,然后根据整数除法法则计算,除到哪一位就在那一位的上面写商,除到最后一位仍除不尽时,添0继续,商的小数点要和被除数的小数点对齐。
小数减法,小数点对齐,把相同数位相减,哪一位不够减就向前一位借一当十与这一位上的数合起来再减。
三位数除以两位数的估算,首先将除数变成近似的整十数,然后根据除数估算被除数,看这个除数乘以几得到和被除数近似的数,商就是几。
含百分数的计算,首先将百分数化成分数或小数后再计算。
35.【答案】解:
=
=
=
=
=()+()
=1+
=
【解析】第一题:先算小括号里面的加法,再算小括号外面的减法;
第二题:按照从左到右的顺序计算;
第三题:运用加法交换律和结合律,把分母相同的两个分数相加。
36.【答案】解:(10×5+10×8+5×8)×2+3.14×4×10+3.14×(4÷2)2
=170×2+125.6+3.14×4
=340+125.6+12.56
=465.6+12.56
=478.16(平方厘米)
【解析】由图可知,该图形的表面积=完成长方体的表面积+圆柱的侧面积+一个圆柱的底面积;长方体的表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积=底面周长×高,圆柱的底面积S=,代入数值计算,即可解答。
37.【答案】解:
【解析】把一个面作为底面,然后确定另外的四个面的位置,根据正方体的特征确定缺少面的位置即可。
38.【答案】解:8×6+8×3.5×2+6×3.5×2-14
=48+56+42-14
=132(平方米)
132×0.8=105.6(千克)
答:粉刷的面积一共有132平方米,共使用了涂料105.6千克。
【解析】粉刷的面积=底面面积+左右两个面的面积+前后两个面的面积-黑板和门窗的面积,粉刷的面积×每平方米使用涂料的质量=一共用涂料的质量。
39.【答案】解:设那一盒水彩笔x元,则
x-10.5=4.5
x=4.5+10.5
x=15
答:那一盒水彩笔15元。
【解析】设那一盒水彩笔x元,根据等量关系:水彩笔的价钱-练习本比水彩笔少的钱数=练习本的价钱,列出方程并解这个方程。
40.【答案】解:设一池水为单位“1”。
在小时内,甲管注水量为,乙管注水量为。
甲管的注水速度是;
乙管的注水速度是。
甲管速度提高25%,即。
乙管速度降低,即。
甲管提高速度后,完成剩余的水量所需时间为小时。
乙管注满一池水的时间为小时。
乙管还需注满B池的时间为小时。
答:乙管还需注满B池的时间为小时。
【解析】需要根据给定的比例关系计算出初始情况下甲、乙两管在小时内分别注入水池的水量,进而求出各自的速度。之后,根据甲管速度提高25%,乙管速度降低,重新计算两管的速度,最后确定甲管注满水池的时间,并据此求出乙管还需的时间。
41.【答案】解:设甲乙两地相距x千米,则从甲地前往乙地的时间为,从乙地返回甲地的时间为4--1.5;
4--1.5=
2.5-=
2.5=
x=18
答:甲乙两地相距18千米。
【解析】已知去乙地与回甲地的速度和全程所花的时间,设甲乙两地之间的距离为未知数x,可用x分别表示去乙地和回甲地的时间,根据题目中全程所花的时间列出方程,解方程即可得到甲乙两地之间的距离。
42.【答案】解:设甲的速度为5x米/分,乙的速度为6x米/分,
5x×50+6x×(50-10)=4900
x=10
5x=50(米/分),
6x=60(米/分);
答:甲的速度为50米/分,乙的速度为60米/分。
【解析】设甲的速度为5x米/分,乙的速度为6x米/分,速度×时间=路程,甲的路程+乙的路程=总路程,据此列方程解答即可。
43.【答案】解:15×2+8×2+10×4+25
=30+16+40+25
=86+25
=111(厘米)
答:至少需要111厘米的彩带。
【解析】根据题意及看图可知彩带由2条长方体礼盒的长、2条宽、4条高和打结处组成,因此,长×2+宽×2+高×4+打结处的长度=彩带的长度。
44.【答案】解:10×8×(5.5-5)
=80×0.5
=40(立方分米)
答:这块石头的体积是40立方分米。
【解析】石头的体积为水位上升部分长方体容器的体积,根据长方体的体积=长×宽×水位上升的高度即可得出答案。
45.【答案】
46.【答案】第二天:+
=+
=;
剩下:1--
=-
=;
答: 第二天修了全长的; 还剩下全长的没有修。
【解析】第二天修了全长的几分之几=第一天修的全长的几分之几+ 第二天比第一天多修了全长的几分之几; 还剩下全长的几分之几没有修=1-第一天修的全长的几分之几-第二天修了全长的几分之几,代入数值计算即可。
47.【答案】解:设一共有x间宿舍。
8x=6(x+4)
8x=6x+24
8x-6x=24
2x=24
x=12
12×8=96(人)
答:参加军训的学生一共有96人。
【解析】可以先设一共有x间宿舍。每间8人需要x间宿舍,每间6人需要(x+4)间宿舍,根据总人数不变列出方程,解方程求出宿舍间数,进而求出总人数即可。
48.【答案】解:+(-)
=+
=(时)
答:乐乐和莉莉每天共排练时。
【解析】乐乐和莉莉每天共排练的时间=乐乐每天排练的时间+莉莉每天排练的时间,其中,莉莉每天排练的时间=乐乐每天排练的时间-小时。
49.【答案】(1)解:8月8日上午10:00到8月10日中午12:00属于24小时以上、48小时以内,
180×=18(元)
答:应扣18元手续费。
(2)解:8月8日上午10:00,再过3小时是8月8日下午13:00,到8月10日中午12:00属于48小时及以上,15天以内;
180×=9(元)
180-9=171(元)
答:能退回171元。
【解析】(1)票价×对应的扣费标准=扣除的费用;
(2)票价×对应的扣费标准=扣除的费用;票价-扣除的费用=能退回的钱数。
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下学期数学期末核心考点突破提分卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、填空题
1.甲、乙两人加工同一种零件,甲加工的零件个数比乙少20%,乙加工的时间比甲少,则乙的工作效率是甲的 %。
2.制作一个棱长为5dm的无盖正方体鱼缸,至少需要 dm2玻璃,可以装 dm3的水。
3.一个长方体的长是5dm,宽4dm,高是2.5dm,它的体积是 dm 。
4.已知 %(M、N、L 均不为0),则M、N、L 这三个数的大小关系是 。
5.学校运动会,参赛运动员在170~180人之间,女运动员人数是男运动员人数的 。女运动员有 人。
6. 一个长方体有两个相对的面是正方形,这个长方体最多有 条棱的长度相等。用12根小棒拼搭只有四个面都是正方形的长方体,肯定 成功。(括号里填“能”或“不能”)
7.2020年盐城成功入选第六届全国文明城市,为此,小娟同学特制一个正方体玩具,展开图如图所示,则原正方体中与“全”字所在面相对的面上的字是 。
8.如图,几个棱长是1分米的正方体堆放在墙角,露在外面的面积是 平方分米,体积一共是 立方分米.
9.李大爷用一批化肥给承包的麦田施肥。若每亩施6千克,则缺少化肥300千克;若每亩施5千克,则余下化肥200千克。那么李大爷共承包了麦田 亩,这批化肥有 千克。
10. =4÷5= = ÷15= (填小数)
11.比较下面数的大小。
0.13
12.一个正方体的 6 个面上分别写着 这 6 个字母,右图是这个正方体的不同摆放, 的对面是
13.一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是 立方厘米。
14.一杯牛奶李明分三次喝,第一次喝了 ,然后加满水;第二次喝了 ,然后再加满水;第三次一饮而尽,李明喝了 杯牛奶, 杯水。
二、判断题
15.甲数是10的 ,乙数的 是6,丙数是6个 ,则乙数>丙数>甲数.( )
16. 12× 和 ×12的意义相同。( )
17.从里连续减去4个 后是 。( )
18.1号点在2号点的南偏西40°方向上,那么2号点在1号点的北偏东40°方向上。( )
19.如果ab≠0,且a
21.两个分数的积一定比这两个分数大。( )
22.用4个同样大小的小正方体能拼成一个大正方体。( )
23.面积单位比长度单位大。( )
三、单选题
24.小西家在小青家东偏北30°方向900米处,则小青家在小西家( )
A.北偏东30°方向900米处 B.西偏南60°方向900米处
C.东偏北60°方向900米处 D.南偏西60°方向900米处
25.一个棱长是4分米的正方体,棱长总和是( )分米。
A.24 B.32 C.48
26.你自己的一只拳头慢慢地伸进装满水的脸盆中,溢出来的水的体积大约是( )
A.小于1毫升,大于1升 B.大于1立方米,小于1升
C.大于1升,小于1立方米 D.大于1毫升,小于1升
27.一根绳子,剪去 后还剩下 米.这根绳子原来长多少米 正确列式是( )。
A. + B. ÷(1- )
C. + × D. ÷
28.小明和小莉出生于2003年12月份,他们的出生日不是同一天,但是都是星期四,且小明比小莉出生早,两个人出生日期之和是22,那么小莉的出生日期是
A.15号 B.16号 C.17号 D.18号
29.林林家在邮局的南偏东40°方向上,则邮局在林林家( )方向上。
A.西偏北40° B.北偏西40° C.东偏南50°
30.把一个圆锥完全浸没在一个底面直径为6厘米的圆柱形容器里,水位上升了4厘米。这个圆锥的体积是( )立方厘米。
A. B. C. D.
31.将一个长方体的高截去5cm就变成了正方体(如图),正方体的表面积比原长方体的表面积减少了60cm2,原长方体的体积是( )立方厘米。
A.27 B.36 C.64 D.72
32.商场的自动扶梯以匀速由下往上行驶,两个孩子嫌扶梯走得太慢,于是在行驶的扶梯上,男孩每秒钟向上走2个梯级,女孩每2秒向上走3个梯级。结果男孩用40秒钟到达,女孩用50秒钟到达。则当该扶梯静止时,可看到的扶梯级有:( )
A.80级 B.100级 C.120级 D.140 级
33.下图中能折成正方体的是( )
A. B. C.
四、计算题
34.直接写出得数。
÷ = 7.2÷0.4= 3.9×0.2= 1-0.92=
2+2%= ×11= × = 271÷89≈
35.用你喜欢的方法计算下面各题。
36.求下面图形的表面积。(单位:cm)
五、作图题
37.在下图中,再给1个格子涂上颜色,使涂色部分折叠后能围成正方体,请你用4种不同的涂法表示。
六、解决问题
38.“十一”期间,学校将每个教室的屋顶和四壁粉刷一新。经测量六(1)班的教室长8米,宽6米,高3.5米,(黑板和门窗共14平方米)粉刷的面积一共有多少平方米?如果每平方米使用涂料0.8千克,粉刷六(1)班的教室共使用了涂料多少千克?
39.一本练习本4.5元,比一盒水彩笔便宜10.5元,那一盒水彩笔多少元钱?(列方程解决问题)
40.甲、乙两个水管同时注两个同样大小的水池,且速度比为 7 : 5,小时之后,两个水池的水量之和刚好是一个满水池的水量 . 此时,甲水管的速度提高 25%,乙水管的速度降低,当甲水管注满水池后,乙水管还要多久才能注满水池
41.老李早上8:00从甲地出发去乙地,每小时行12千米,在乙地办事用去1.5小时,为了赶在12:00回家吃午饭,他把速度提高了,请问甲乙两地相距多少千米?
42.甲、乙两人分别从相距4900米的A、B两地出发,相向而行,甲出发10分钟后乙才出发,甲、乙的速度比为5:6甲出发50分钟后两人相遇,他们的速度各是多少?
43.一个礼盒(如下图),像这样用彩带捆扎起来,至少需要多长的彩带?(打结处需要25厘米)
44.一个长10dm,宽8dm,高7dm的长方体容器装有5dm深的水,放入一块石头完全沉入水中,水面上升到5.5dm处。这块石头的体积是多少立方分米?
45.自古至今,宣纸就是创作中国书画的最佳材料。为了迎接学校书法比赛,五年级一班买来一批宣纸供大家练习使用,第一次用去了这批宣纸的,第二次用去了这批宣纸的,还剩下这批宣纸的几分之几没有用?
46.修一条 千米长的公路,第一天修了全长的 ,第二天比第一天多修了全长的 。第二天修了全长的几分之几?还剩下全长的几分之几没有修?
47.老师为参加军训的同学安排宿舍,如果每间宿舍住8人,那么这些宿舍正好住满;如果每间宿舍住6人,那么正好缺4间宿舍。参加军训的学生一共有几人
48.惠东渔歌俗称“后船歌”,是流行于港口、巽寮、稔山、盐洲等地渔村的传统音乐,是惠州市第一个国家级“非遗”。为了让更多学生了解民间传统音乐,实验小学第二课堂开设了渔歌课,乐乐每天排练时,比莉莉每天多排练时。乐乐和莉莉每天共排练多少时?
49.李叔叔准备去外地出差,在铁路12306网站上买了一张8月10日中午12:00发车的高铁票,票价为180元,他在8月8日上午10:00接到取消出差的通知。按照规定,火车票退票需要扣除手续费,规定如下表。
距离开车时间 15天以上(不含15天) 48小时及以上,15天以内 24小时以上、48小时以内 24小时以内
退票手续费 免费 票面价的 票面价的 票面价的
(1)如果李叔叔接到取消出差的通知后立即申请退票,那么应扣多少元手续费?
(2)如果李叔叔收到取消出差通知后,过了3小时才申请退票,那么能退回多少钱?
参考答案及试题解析
1.【答案】150
【解析】解:假设乙加工的零件总数是1,甲加工的时间是1。
=
=
=
=1.5×100%
=150%
故答案为:150
【分析】根据题意,把乙加工的零件总数看作单位“1”,则甲加工的零件总数是(1-20%);把甲加工的时间看作单位“1”,则乙加工的时间是);根据“工作效率=工作总量÷工作时间”,分别求出甲乙的工作效率,用乙的工作效率÷甲的工作效率×100%即可求解。
2.【答案】125;125
【解析】解:5×5×5
=25×5
=125(dm2),
所以需要125dm2玻璃;
5×5×5
=25×5
=125(dm3),
所以可以装125dm3的水。
故答案为:125;125。
【分析】至少需要玻璃的面积=棱长×棱长×5;水的体积(容积)=棱长×棱长×棱长,代入数值计算即可。
3.【答案】50
【解析】解:5×4×2.5=50dm3,所以它的体积是50dm3。
故答案为:50。
【分析】长方体的体积=长×宽×高,据此作答即可。
4.【答案】M=N=L
【解析】解:因为 N×0.375,L×37.5%=L×0.375,所以M=N=L。
故答案为:M=N=L。
【分析】把除法转化成乘法,同时把分数、百分数都化成小数,这样就能判断三个字母表示数的大小。
5.【答案】75
【解析】女运动员:男运动员=3:4,女运动员占总人数的;
180÷7 =25(人)……5(人)
25×5= 175(人)
175×=75(人)
故答案为:75。
【分析】已知女运动员人数是男运动员人数的 ,也就是女运动员:男运动员=3:4,如果把女运动员人数看作3份,男运动员就是4份,总份数就是:3+4=7份, 女运动员占总人数的,人数在 170~180人 , 能被7整除,这个数是180÷7 =25……5,人数应该是25×5= 175人,女运动员占总人数的,用175×即可解答。
6.【答案】8;不能
【解析】解:这个长方体最多有8条棱的长度相等;用12根小棒拼搭只有四个面都是正方形的长方体,肯定不能成功。
故答案为:8;不能。
【分析】长方体有两个相对的面是正方形,每个正方形有4条棱,所以长方体最多有8条棱的长度相等;
长方体最多有2个面是正方形。
7.【答案】明
【解析】解:原正方体中与“全”字所在面相对的面上的字是明。
故答案为:明。
【分析】在正方体的展开图中,相对面的特征:“Z”字型的两端;三个正方形排成的一行的两端的正方形。
8.【答案】12;6
【解析】解:3+5+4=12(个)
12×1=12(平方分米)
1×1×1×6=6(立方分米)
故答案为:12;6.
【分析】小正方体露在外面的面分成三部分:正面、上面、侧面,分别查出这几个面是多少,再计算露在外面的面积,露在外面的面积=一个小正方形的面积×露在外面的小正方形的个数。
9.【答案】500;2700
【解析】解:设承包了麦田x亩,则化肥有6x-300千克,根据题意可得,
6x-300-5x=200
解得
x=500,
6x-300=6×500-300=2700(千克);
答:李大爷共承包了麦田500亩,这批化肥有2700千克
故答案为:500,2700
【分析】设承包了麦田x亩,则化肥有6x-300千克,根据题意可得等量关系:化肥的总千克数(6x-300千克)-麦田的亩数x5千克=200千克,由此可得方程解决问题
10.【答案】16;45;12;0.8
【解析】解:4÷5=0.8
20×0.8=16
36÷0.8=45
15×0.8=12
4÷5=0.8
20×0.8=16
36÷0.8=45
15 × 0.8=12
故答案为:16,45,12,0.8
【分析】分数的分子和分母可以看作是除法的被除数和除数,分数的值就是除法的商。同时,分数的值也可以转换为小数,即分子除以分母。
11.【答案】>;<;=;>
【解析】>;<;0.13=;>=。
故答案为:>;<;=;>。
【分析】同分母相同,分子大的分数大;分子相同,分母大的分数反而小。
异分母分数比较大小,先通分将分数化成同分母分数,再比较大小。
小数与分数比较大小,先将小数化成分数,再比较大小。
小数化分数的方法:①原来有几位小数,就在1 后面写几个零作分母,②原来的小数去掉小数点作分子。注意:化成分数后,能约分的要约分。
12.【答案】D
【解析】由图2和图3可以看出,与D相邻的四个面分别是E、F、B、C,因此A的对面是D。
故答案为:D
【分析】要找出A的对面,可先确定与A相邻的四个面,与A不相邻的面即为它的对面。
13.【答案】54
【解析】解:依题意,这个长方体的长、宽、高之和是 (厘米),
于是它的宽与高都等于 (厘米),
它的长是(厘米)。
所以这个 长方体的各条棱长的和是48厘米 是 (立方厘米)。
故答案为:54
【分析】 根据“长是宽的2倍,高与宽相等”,可以把宽和高看成1份,则长为2份, 再根据长方体的各条棱长的和是48厘米,可以求出长方体的长宽高,最后根据 长方体的体积等于长乘宽乘高计算即可。
14.【答案】1;
【解析】解:李明喝了1杯牛奶;+=。
故答案为:1;。
【分析】第三次一饮而尽,说明李明把牛奶全部喝完,即喝了1杯牛奶;喝水的分率=第一次喝的分率+第二次喝的分率。
15.【答案】错误
【解析】解:甲数:10×=6,乙数:6÷=10,丙数=6×=4,4<6<10,所以乙数>甲数>丙数。
故答案为:错误。
【分析】一个数的几分之几是另一个数,那么另一个数=这个数×几分之几,这个数=另一个数÷几分之几;求几个相同加数的和,用这个相同加数×相同加数的个数。最后把三个数进行比较即可。
16.【答案】错误
【解析】12× 表示求12的 是多少, ×12表示求 的12倍是多少,因此原题说法错误。
故答案为:错误
【分析】12× 表示求12的 是多少, ×12表示求 的12倍是多少,因此12× 和 ×12的意义相同的说法错误,即可解答。
17.【答案】正确
【解析】
=
=
故答案:正确
【分析】按题目中的条件列出算式后,应先算乘法,再算减法,结果是,所以答案正确。在分数混合运算中要先算乘除法,再算加减法,最后就可以求出结果。
18.【答案】正确
【解析】解:2号点在1号点的北偏东40°方向上。说法正确。
故答案为:正确。
【分析】甲在乙什么方向和乙在甲什么方向,这两个方向相反,度数和距离不变,据此解答。
19.【答案】正确
【解析】解:a
故答案为:正确。
【分析】在除法计算中,被除数不变,除数越大,商越小。
20.【答案】正确
【解析】正方体和长方体都可以用底面积乘相应的高求它的体积来进行计算,这种说法是正确的。故答案为:正确。
【分析】根据长方体与正方体的体积定义可知:正方体与长方体都可以用“底面积×高”求体积。对的。因为正方体的体积V=a×a×a,其中a×a可以看作是正方体的底面积;长方体的体积V=a×b×h,其中a×b是长方体的底面积,所以正方体和长方体的体积都可以用底面积乘高来计算。考察了正方体和长方体的体积公式。
21.【答案】错误
【解析】两个分数的积可能比这两个分数大。
故答案为:错误。
【分析】一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小,据此进行判断。
22.【答案】错误
【解析】2×2×2=8,小正方体拼大正方体,最少需要8个,本题错。
故答案为:错误。
【分析】大正方体最小时,一边有两个正方体,一共需要8个正方体。
23.【答案】错误
【解析】错误。体积单位、面积单位、长度不是同一类单位,不能比较大小
【分析】
体积单位、面积单位、长度不是同一类单位,不能比较大小,据此判断.解答本题关键是明白:只有同一类单位,才能比较大小.
24.【答案】D
【解析】解:小西家在小青家东偏北30°方向900米处,则小青家在小西家西偏南30°方向900米处或者南偏西60°方向900米处。
故答案为:D。
【分析】观察的中心相反,如果度数不变,那么方向刚好相反,也可以通过画图帮助理解方向。
25.【答案】C
【解析】4×12=48(分米)
【分析】正方体总共有12条棱,并且每条棱的长度都是一样,所以知道了每条棱的长度,就用4分米乘以12即可。
26.【答案】D
【解析】解:1立方米>1升>1毫升,
A、B描述错误,C不合适,单位过大,
故选:D。
【分析】溢出的水的体积等于拳头的体积,一个人一只拳头的体积大于1毫升,小于1升。
27.【答案】B
【解析】
故答案为:B。
【分析】把一根绳子看作单位“1”,数量之间存在以下相等关系:绳子原来的长度×(1-)=剩下绳子长度。
28.【答案】D
【解析】解:设小明的出生日期为x,那么小莉的出生日期就是x+7、x+14、x+21等,
如果他们相差7天,那么我们可以列出等式x+(x+7)=22,解出x=7.5,这不符合实际情况,所以我们舍去这种情况.
如果他们相差14天,那么我们可以列出等式x+(x+14)=22,解出x=4,这时符合题意,那么小莉的出生日期就是x+14=4+14=18.
如果他们相差21天,那么我们可以列出等式x+(x+21)=22,解出x=0.5,这不符合实际情况,所以我们舍去这种情况.
因此,小莉的出生日期应该是18号.
故答案为:D。
【分析】设小明的出生日期为x,那么小莉的出生日期就是x+7、x+14、x+21等,我们需要找到符合所有条件的解。
29.【答案】B
【解析】解:林林家在邮局的南偏东40°方向上,则邮局在林林家北偏西40°方向上。
故答案为:B。
【分析】如图:邮局在林林家北偏西40°方向或西偏北50°方向。
30.【答案】A
31.【答案】D
32.【答案】B
【解析】解:设电梯匀速时的速度为x,
(x+)×50=(x+2)×40
50x+75=40x+80
50x-40x=80-75
10x=5
x=0.5
扶梯静止时可看到的扶梯级数:(2+0.5)×40=100。
故答案为:B。
【分析】这是一个典型的行程问题的变型,总路程为“扶梯静止时可看到的扶梯级”,速度为“男孩或女孩每个单位向上运动的级数”。先列方程求出电梯匀速时的速度,然后求出扶梯静止时可看到扶梯的级数即可。
33.【答案】C
【解析】解:根据正方体展开图的11种特征,选项A、选项B不能折成正方体;选项C能折成正方形.
故选:C.
【分析】根据正方体展开图的11种特征,选项A中有长方形,不属于正方体展开图(它是长方体展开图),不能折成正方体;选项B不属于正方体展开图,不能折成正方体;选项C都属于正方体展开图的“1﹣4﹣1”型,能折成正方形.
34.【答案】 ÷ =3 7.2÷0.4=18 3.9×0.2=0.78 1-0.92=0.08
2+2%=2.02 ×11=19 × = 271÷89≈3
【解析】分数与分数相乘,分子乘以分子作为积的分子,分母乘以分母作为积的分母;
一个数除以分数等于这个数乘以这个分数的倒数;
小数乘法按照整数乘法法则计算,最后看因数中一共有几位小数,就在积的末尾查出几位小数点上小数点,小数位数不够时,在积的前面用0补齐。
小数除法,根据除法的性质将除数化成整数,然后根据整数除法法则计算,除到哪一位就在那一位的上面写商,除到最后一位仍除不尽时,添0继续,商的小数点要和被除数的小数点对齐。
小数减法,小数点对齐,把相同数位相减,哪一位不够减就向前一位借一当十与这一位上的数合起来再减。
三位数除以两位数的估算,首先将除数变成近似的整十数,然后根据除数估算被除数,看这个除数乘以几得到和被除数近似的数,商就是几。
含百分数的计算,首先将百分数化成分数或小数后再计算。
35.【答案】解:
=
=
=
=
=()+()
=1+
=
【解析】第一题:先算小括号里面的加法,再算小括号外面的减法;
第二题:按照从左到右的顺序计算;
第三题:运用加法交换律和结合律,把分母相同的两个分数相加。
36.【答案】解:(10×5+10×8+5×8)×2+3.14×4×10+3.14×(4÷2)2
=170×2+125.6+3.14×4
=340+125.6+12.56
=465.6+12.56
=478.16(平方厘米)
【解析】由图可知,该图形的表面积=完成长方体的表面积+圆柱的侧面积+一个圆柱的底面积;长方体的表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积=底面周长×高,圆柱的底面积S=,代入数值计算,即可解答。
37.【答案】解:
【解析】把一个面作为底面,然后确定另外的四个面的位置,根据正方体的特征确定缺少面的位置即可。
38.【答案】解:8×6+8×3.5×2+6×3.5×2-14
=48+56+42-14
=132(平方米)
132×0.8=105.6(千克)
答:粉刷的面积一共有132平方米,共使用了涂料105.6千克。
【解析】粉刷的面积=底面面积+左右两个面的面积+前后两个面的面积-黑板和门窗的面积,粉刷的面积×每平方米使用涂料的质量=一共用涂料的质量。
39.【答案】解:设那一盒水彩笔x元,则
x-10.5=4.5
x=4.5+10.5
x=15
答:那一盒水彩笔15元。
【解析】设那一盒水彩笔x元,根据等量关系:水彩笔的价钱-练习本比水彩笔少的钱数=练习本的价钱,列出方程并解这个方程。
40.【答案】解:设一池水为单位“1”。
在小时内,甲管注水量为,乙管注水量为。
甲管的注水速度是;
乙管的注水速度是。
甲管速度提高25%,即。
乙管速度降低,即。
甲管提高速度后,完成剩余的水量所需时间为小时。
乙管注满一池水的时间为小时。
乙管还需注满B池的时间为小时。
答:乙管还需注满B池的时间为小时。
【解析】需要根据给定的比例关系计算出初始情况下甲、乙两管在小时内分别注入水池的水量,进而求出各自的速度。之后,根据甲管速度提高25%,乙管速度降低,重新计算两管的速度,最后确定甲管注满水池的时间,并据此求出乙管还需的时间。
41.【答案】解:设甲乙两地相距x千米,则从甲地前往乙地的时间为,从乙地返回甲地的时间为4--1.5;
4--1.5=
2.5-=
2.5=
x=18
答:甲乙两地相距18千米。
【解析】已知去乙地与回甲地的速度和全程所花的时间,设甲乙两地之间的距离为未知数x,可用x分别表示去乙地和回甲地的时间,根据题目中全程所花的时间列出方程,解方程即可得到甲乙两地之间的距离。
42.【答案】解:设甲的速度为5x米/分,乙的速度为6x米/分,
5x×50+6x×(50-10)=4900
x=10
5x=50(米/分),
6x=60(米/分);
答:甲的速度为50米/分,乙的速度为60米/分。
【解析】设甲的速度为5x米/分,乙的速度为6x米/分,速度×时间=路程,甲的路程+乙的路程=总路程,据此列方程解答即可。
43.【答案】解:15×2+8×2+10×4+25
=30+16+40+25
=86+25
=111(厘米)
答:至少需要111厘米的彩带。
【解析】根据题意及看图可知彩带由2条长方体礼盒的长、2条宽、4条高和打结处组成,因此,长×2+宽×2+高×4+打结处的长度=彩带的长度。
44.【答案】解:10×8×(5.5-5)
=80×0.5
=40(立方分米)
答:这块石头的体积是40立方分米。
【解析】石头的体积为水位上升部分长方体容器的体积,根据长方体的体积=长×宽×水位上升的高度即可得出答案。
45.【答案】
46.【答案】第二天:+
=+
=;
剩下:1--
=-
=;
答: 第二天修了全长的; 还剩下全长的没有修。
【解析】第二天修了全长的几分之几=第一天修的全长的几分之几+ 第二天比第一天多修了全长的几分之几; 还剩下全长的几分之几没有修=1-第一天修的全长的几分之几-第二天修了全长的几分之几,代入数值计算即可。
47.【答案】解:设一共有x间宿舍。
8x=6(x+4)
8x=6x+24
8x-6x=24
2x=24
x=12
12×8=96(人)
答:参加军训的学生一共有96人。
【解析】可以先设一共有x间宿舍。每间8人需要x间宿舍,每间6人需要(x+4)间宿舍,根据总人数不变列出方程,解方程求出宿舍间数,进而求出总人数即可。
48.【答案】解:+(-)
=+
=(时)
答:乐乐和莉莉每天共排练时。
【解析】乐乐和莉莉每天共排练的时间=乐乐每天排练的时间+莉莉每天排练的时间,其中,莉莉每天排练的时间=乐乐每天排练的时间-小时。
49.【答案】(1)解:8月8日上午10:00到8月10日中午12:00属于24小时以上、48小时以内,
180×=18(元)
答:应扣18元手续费。
(2)解:8月8日上午10:00,再过3小时是8月8日下午13:00,到8月10日中午12:00属于48小时及以上,15天以内;
180×=9(元)
180-9=171(元)
答:能退回171元。
【解析】(1)票价×对应的扣费标准=扣除的费用;
(2)票价×对应的扣费标准=扣除的费用;票价-扣除的费用=能退回的钱数。
21世纪教育网(www.21cnjy.com)
同课章节目录
