2024-2025学年期末全真模拟培优卷(含解析)三年级下册数学(北师大版)
文档属性
| 名称 | 2024-2025学年期末全真模拟培优卷(含解析)三年级下册数学(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 234.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 16:56:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年三年级下册数学期末全真模拟培优卷(北师大版)
一、填空题
1.等腰三角形、圆都是 图形,等腰三角形有 条对称轴,圆有 条对称轴。
2.老师拿来了一堆糖果,分给同学们。每人分8颗,最后还剩下6颗,如果再拿来18颗,正好可以给每个同学再分2颗。请问:原来共有 颗。
3.根据a×b=480,直接写出下面算式的得数。
a×(b×2)= (a×2)×(b×3)=
(a÷5)×b= (a×10)×(b÷10)=
4.在横线上填上“>”“<”或“=”。
7厘米 70毫米 300秒 3分 360+20 600
36分米 3米 9000克 1吨 46+27 47+26
5.在算式 ÷6=19……△中,余数最大是 ,这时被除数是 。
6.□÷7=15……☆,☆最大是 ,这时□是 。
7.一个长方形花坛的面积是100平方米,如果它的长扩大到原来的5倍,宽不变,扩建后花坛的面积是 平方米。
8.狗大约能活9年,鳄鱼大约能活182年。鳄鱼的寿命大约是狗的 倍。
9.如图,个相同的长方形和个小正方形拼成一个大正方形,已知其中小正方形的面积为平方厘米,大正方形的面积为平方厘米,则其中长方形的长为 厘米,宽 厘米.
10.2022年,北京将主办第24届冬季奥林匹克运动会。24个2022相乘,积的个位数字是 。
11.同学们,本学期老师让大家做荡秋千的活动中,你发现在相同时间内,荡秋千的次数与 有关。
12.小雨、小东、小松三个人进行跳绳比赛.小松说:“我不是最后一名.”小东说:“我也不是最后一名,但小松的成绩比我好.”那么 是第一名, 是最后一名.
二、判断题
13.周长相等的两个长方形面积一定相等。( )
14.计算25×30时,可以先算出25×3=75,再在末尾加一个0。( )
15.两位数乘两位数:□5×□8,积的末尾只有一个0。( )
16.拉抽屉时抽屉的运动是平移。( )
17.三位数除以一位数商可能是两位数。(
)
18.小芳用一周的时间把一本书看完了,每天看的页数相同,那么3天她看了全书的。( )
19.周长相等的两个正方形,它们的面积一定相等。( )
三、单选题
20.与1吨最接近的是( )。
A.999克 B.9千克 C.990千克 D.1001克
21.要使 89÷5的商是两位数, 里可以填( )。
A.6~9 B.0~4 C.1~4
22.有两个同样大小的杯子,里面都倒满了牛奶,欣欣喝了这杯牛奶的 ,小雨喝了这杯牛奶的 ,( )剩下的牛奶多。
A.欣欣 B.小雨 C.一样多
23.把2盒饼干平均分给6个小朋友,其中4个小朋友分得这些饼干的( )。
A. B. C.
24.下图可以看作是一个等腰直角三角形旋转若干次后形成的,每次旋转的度数是( )。
A.90° B.60° C.45° D.30°
25.一个长方形的长和一个正方形的边长相等,它的面积( )。
A.长方形比正方形大
B.长方形比正方形小
C.长方形和正方形相等
26.一条公路七天修完了 ,三天修了这条路的( )
A. B. C. D.
27.利用数学知识进行分析,下列叙述合理的是( )。
A.课桌的高度是20分米 B.正常成年人步行速度为每分钟60米
C.一个西瓜重100千克 D.一个保温杯的容积是500L
28.下列各图案中不是轴对称是( )。
A. B. C. D.
29.680÷8商末尾的0有( )。
A.3个 B.2个 C.0个
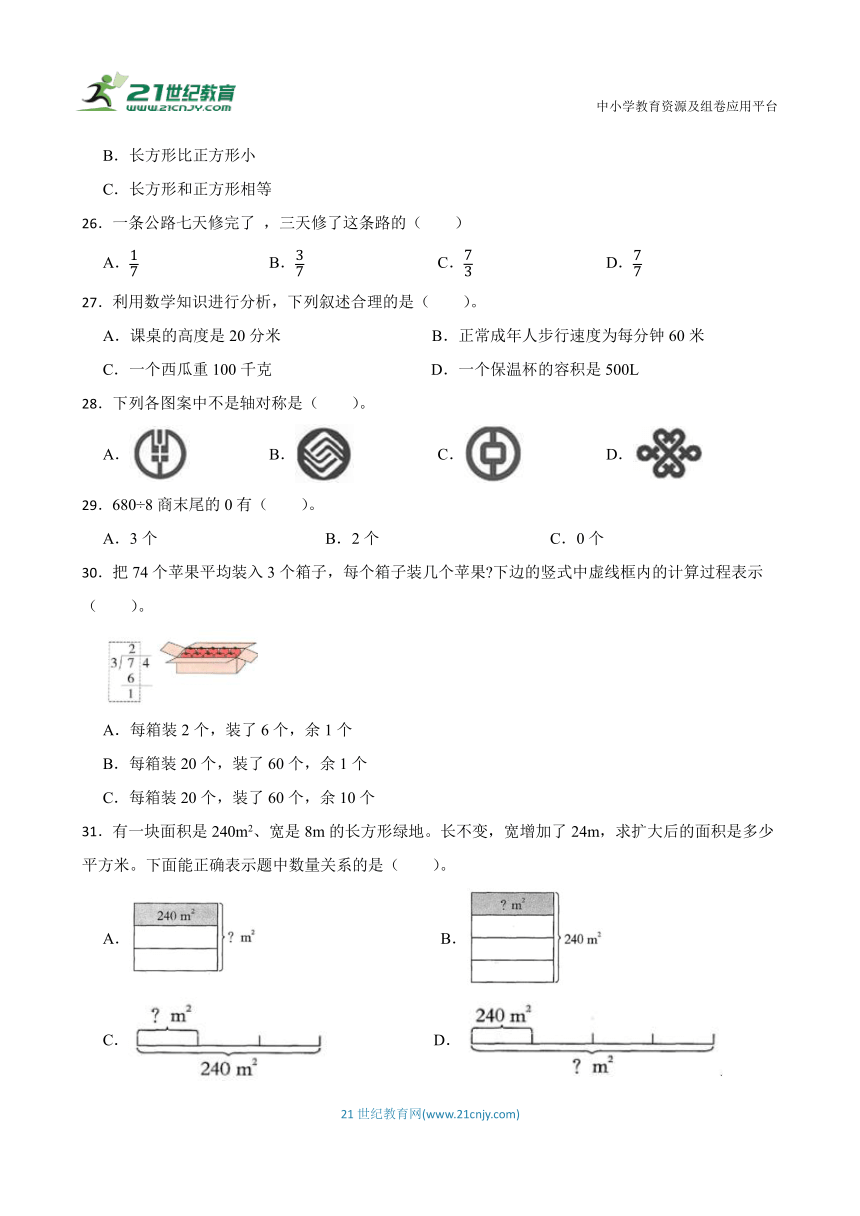
30.把74个苹果平均装入3个箱子,每个箱子装几个苹果 下边的竖式中虚线框内的计算过程表示( )。
A.每箱装2个,装了6个,余1个
B.每箱装20个,装了60个,余1个
C.每箱装20个,装了60个,余10个
31.有一块面积是240m2、宽是8m的长方形绿地。长不变,宽增加了24m,求扩大后的面积是多少平方米。下面能正确表示题中数量关系的是( )。
A. B.
C. D.
四、计算题
32.口算
6×12= 25×3= 60×70= 10×73=
42÷3= 9×800= 13×40= 10-10÷2=
50×40= 560÷8= 80×25=
80+90=
33.递等式计算。
(83+57)÷4 244+6×28 352-(152-89)
34.列竖式计算。(带★的要验算)
58×84= ★10-4.7= 918÷9= ★709÷6=
35.计算下面图形的面积。(单位:厘米)
(1)
五、作图题
36.请按照要求作图。
①先根据对称轴,画出对称图形的另一半。
②画出这个轴对称图形先向上平移2格,再向右平移4格后的图形。
六、解决问题
37.对农直播电商结合直播技术和农产品销售,实现了农村经济的增长和农民的增收。某直播间第一天销售了红薯库存的 ,第二天比第一天少卖全部库存的 ,则还剩全部库存的几分之几没有售出?
38.黄豆的营养价值很高, 10kg黄豆含3.5kg蛋白质、1.55kg膳食纤维、1.6kg脂肪、1.87kg碳水化合物,另含有许多微量元素。照这样计算,lt黄豆含有多少千克膳食纤维?
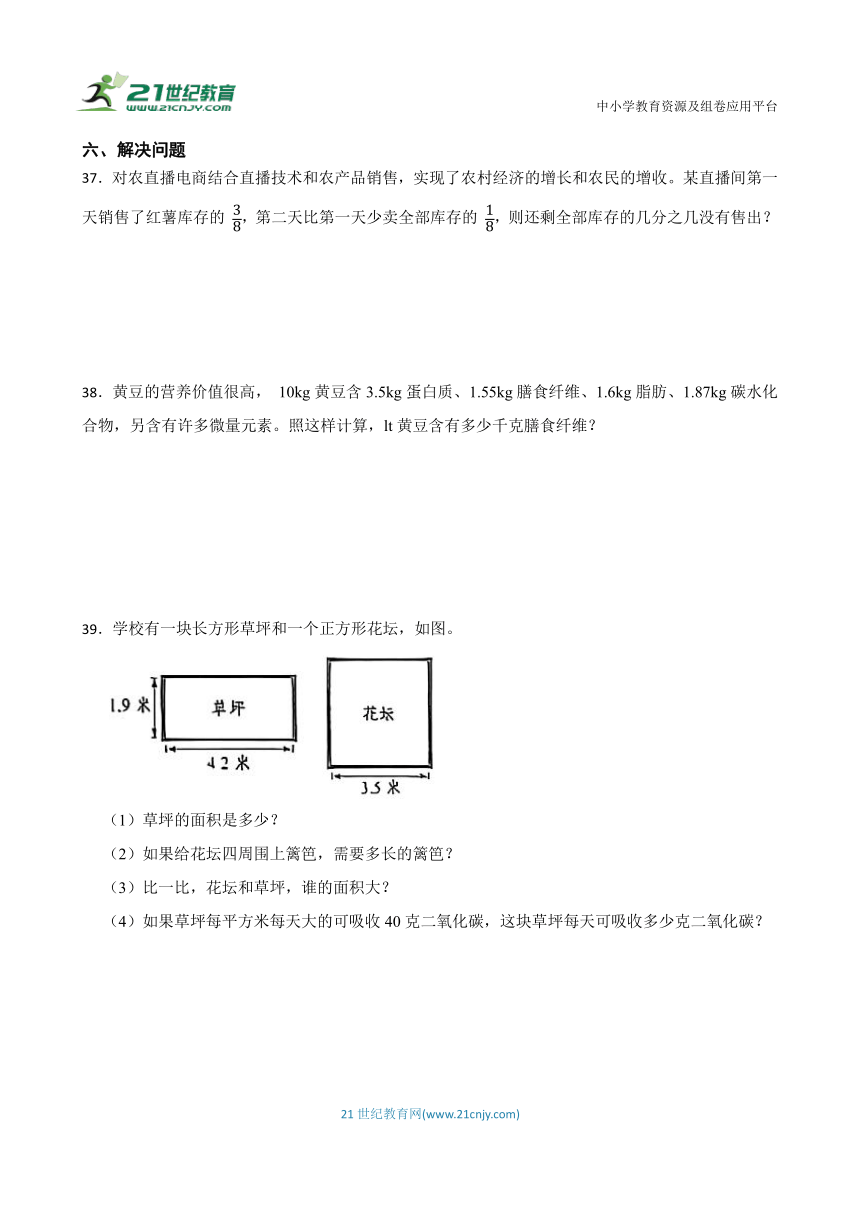
39.学校有一块长方形草坪和一个正方形花坛,如图。
(1)草坪的面积是多少?
(2)如果给花坛四周围上篱笆,需要多长的篱笆?
(3)比一比,花坛和草坪,谁的面积大?
(4)如果草坪每平方米每天大的可吸收40克二氧化碳,这块草坪每天可吸收多少克二氧化碳?
40.王老师带着36名同学去儿童乐园,带了500元,够买门票够吗?
41.佛山大剧院是佛山新城文化艺术中心的核心组成部分,位于佛山市文化中心坊塔内东侧。为促进学生全面发展,增强学生体质健康,学期结束,伴着明媚阳光和雀跃的心情,实验小学三年级学生在老师的带领下,前往佛山市文化中心,开展一次有意义的综合社会实践活动。实验小学9个班共414名同学,由12位老师带领乘大巴前往目的地,一辆大巴可以坐35人,租12辆大巴够吗?
42.益民商店每付乒乓球拍39元,李老师准备给学校乒乓球队买16付乒乓球拍,他带了600元钱,李老师带的钱够吗?
43.社区宣传员在向社区居民做“防网络诈骗”宣传工作,安排了一些工作人员向居民发放宣传单。张阿姨7分钟发了266张,李叔叔4分钟发了156张。他们两人中,谁平均每分钟发放的宣传单多?
44.王老师计划给他家的厨房铺地砖,他设计了两种方案。(对应作业目标:3507,3508)
方案一:用边长是2分米的正方形地砖,每块地砖3元。
方案二:用长3分米、宽2分米的长方形地砖,每块地砖4元。
(1)方案一要用300块地砖。厨房地面的面积是多少平方米
(2)方案二要用多少块地砖
(3)哪种方案便宜
45.学校会议室的地面是长方形,长9米,宽6米。用边长3分米的正方形地砖铺满这间会议室的地面,一共要用多少块这样的地砖?
46.金山旅行社推出“莲花山景区一日游”的两种出游价格方案。成人4人,儿童6人,选哪个方案买票比较合算?请通过计算简单说明理由。
方案一:成人120元/人,儿童50元/人;
方案二:团体10人以上(包含10人),100元/人。
47.爷爷想围一个面积48平方米的长方形鸡圈,爷爷可以怎样围?最少需要篱笆长多少米?(长和宽都取整米数)
48.300名同学去春游,怎样租车最省钱?
参考答案及试题解析
1.【答案】轴对称;1;无数
【解析】等腰三角形、圆都是轴对称图形,等腰三角形有1条对称轴,圆有无数条对称轴。
故答案为:轴对称;1;无数。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
2.【答案】102
【解析】解:同学人数:(18+6)÷2=12(人),
原来树苗数量:
8×12+6
=96+6
=102(棵),
答:原来共有102棵树苗。
故答案为:102
【分析】 由题意,每人分8棵树苗,最后还剩下6棵,如果再拿来18棵,正好可以给每个同学再分2棵,即每人多分给2棵,就多分了(6+18)棵,由此可求得共有多少个同学,进而求得原来共有多少棵树苗.
3.【答案】960;2880;96;480
【解析】解:a×(b×2)=960;(a×2)×(b×3)=2880
(a÷5)×b=96;(a×10)×(b÷10)=480。
故答案为:960;2880;96;480。
【分析】两个数相乘,一个乘数不变,另一个乘数扩大或缩小多少倍(0除外),积就扩大或缩小相同的倍数。两个数相乘,一个乘数扩大或缩小多少倍(0除外),另一个乘数缩小或扩大相同的倍数,积不变。
4.【答案】=;>;<;>;<;=
【解析】7厘米=70毫米;
因为3分=180秒,300秒>180秒,所以300秒>3分;
因为360+20=380,380<600,所以360+20<600;
因为3米=30分米,36分米>30分米,所以36分米>3米;
因为1吨=1000千克=1000000克,9000克<1000000克,所以9000克<1吨;
因为46+27=73,47+26=73,所以46+27=47+26。
故答案为:=;>;<;>;<;=。
【分析】根据1厘米=10毫米,1分=60秒,1米=10分米,1吨=1000千克,1千克=1000克,将单位化统一,再比较大小;
比较两个算式的大小,先分别计算出得数,再比较大小。
5.【答案】5;119
【解析】解:在算式 ÷6=19……△中,余数最大是5,
这时被除数=19×6+5
=114+5
=119。
故答案为:5;119。
【分析】在有余数的除法算式中,余数一定比除数小,所以除数已知时,余数最大=除数-1,再根据被除数=商×除数+1计算即可得出答案。
6.【答案】6;111
7.【答案】500
【解析】解:100×5=500(平方米),
所以扩建后花坛的面积是500平方米。
故答案为:500。
【分析】长方形的面积=长×宽,积的变化规律:一个因数不变,另一个因数扩大几倍(倍数不为0),积就扩大几倍,本题中扩建后的面积=扩大前的面积×长扩大的倍数,代入数值计算即可。
8.【答案】20
【解析】解:182÷9=20。
故答案为:20。
【分析】鳄鱼的寿命大约是狗寿命的倍数=鳄鱼的寿命÷狗的寿命。
9.【答案】11;9
【解析】解:400=20×20
所以大正方形的边长是20厘米;
4=2×2
所以小正方形的边长是2厘米;
(20-2)÷2
=18÷2
=9(厘米)
(400-4)÷4÷9
=396÷4÷9
=99÷9
=11(厘米);
答:长方形的长是11厘米.宽是9厘米.
故答案为:11,9.
【分析】大正方形面积是400平方厘米,边长应是20厘米;小正方形面积是4平方厘米,边长应是2厘米;大正方形边长减去小正方形边长正好等于长方形的两个宽,所以长方形的宽应是(20-2)÷2=9(厘米);根据“长方形的长=面积÷宽”,代入数值进行解答即可.
10.【答案】6
【解析】解:2=2,个位是2
2×2=4,个位是4
2×2×2=8,个位是8
2×2×2×2=16,个位是6
2×2×2×2×2=32,个位是2
2×2×2×2×2×2=64,个位是4
……
即每4个2相乘,积的个位就会出现循环;
24÷4=6....0
则24个2相乘,积的个位数字是与每组的第4个数字相同,即6。
故答案为:6。
【分析】根据题意,2022的个位是2,其积的个位数字只与2有关;从n个2相乘所得积的个位数字寻找规律,发现每4个2相乘,积的个位就会出现循环,用24÷4发现余数为0,说明个位数字是每个循环里最后一个数,即6。
11.【答案】绳子长短
【解析】解:在相同时间内,荡秋千的次数与物体质量无关,与绳子长短有关。
故答案为:绳子长短。
【分析】在相同时间内,同一个秋千(摆长不变),荡的次数是不变的,而且与质量无关,绳子的长度越长,周期越大,频率越小,所以次数就变小,据此解答即可。
12.【答案】小松;小雨
【解析】根据题意,由小松和小东都不是最后一名可知,小雨是最后一名;
由小东说小松的成绩比他好可知,小松是第一名。所以:小松是第一名,小雨是最后一名。
故答案为:小松;小雨。
【分析】小松说:“我不是最后一名。”小东说:“我也不是最后一名。”所以小雨是最后一名,又因为小东说:“小松的成绩比我好.”所以小松是第一名。
13.【答案】错误
【解析】解:周长相等的两个长方形面积不一定相等。
故答案为:错误。
【分析】其中一个长方形的长和宽分别是4和2,那么它的周长是(4+2)×2=12,面积是4×2=8;另一个长方形的长和宽分别是5和1,那么它的周长是(5+1)×2=12,面积是5×1=5,所以它们周长相等但是面积不相等。
14.【答案】正确
15.【答案】错误
【解析】解:如:25×48=1200,积的末尾有2个0;
15×28=420,积的末尾只有一个0,所以原题干说法错误。
故答案为:错误。
【分析】两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
16.【答案】正确
【解析】根据平移的基本知识,拉抽屉时抽屉的运动是平移,只发生了位置变动,大小不变。
【分析】考查基本的平移知识
17.【答案】正确
【解析】解:三位数除以一位数商可能是两位数,也可能的三位数。
故答案为:正确。
【分析】三位数除以一位数,如果被除数百位上的数字大于或等于除数,商是三位数;如果被除数百位上的数字小于除数,商是两位数。
18.【答案】错误
【解析】解:++
=+
=。
故答案为:错误。
【分析】一周是7天,小芳用一周的时间把一本书看完了,并且每天看的页数相同,则她每天看全书的,3天她看了全书的。
19.【答案】正确
【解析】解:周长相等的两个正方形,它们的面积一定相等,原题干说法正确。
故答案为:正确。
【分析】正方形的面积=边长×边长,周长相等的两个正方形,边长=周长÷4,边长相等,则它们的面积一定相等。
20.【答案】C
【解析】与1吨最接近的是990千克。
故答案为:C。
【分析】根据1吨=1000千克,对比各选项的数,即可得到最接近1吨的数,据此解答。
21.【答案】C
【解析】解:里可以填1~4中任何一个数。
故答案为:C。
【分析】三位数除以一位数,如果首位够除,那么商是三位数,如果首位不够除,那么商是两位数。
22.【答案】B
【解析】解:,因为小雨喝的少,所以剩下的就多。
故答案为:B。
【分析】有两个同样大小的杯子,里面都倒满了牛奶,喝的少的,剩下的就多。
23.【答案】A
【解析】解:4÷6=。
故答案为:A。
【分析】4个小朋友分得这些饼干的分率=4÷平均分给小朋友的人数。
24.【答案】C
【解析】等腰直角三角形的一个直角是90度,另外两个底角是45度,所以可以看作是一个等腰直角三角形每次旋转的45度后形成的。
故答案为:C。
【分析】在旋转时,旋转中心不变,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角。这个图中的旋转角正好是等腰直角三角形的一个底角。
25.【答案】B
【解析】解:长方形的面积比正方形的面积小。
故答案为:B。
【分析】长方形的面积=长×宽,正方形的面积=边长×边长,因为长方形的长和正方形的边长相等,长方形的宽小于正方形的边长,所以长方形的面积比正方形的面积小。
26.【答案】B
【解析】解:三天修了这条路的。
故答案为:B。
【分析】每天修了这条路的,那么3天修了这条路的。
27.【答案】B
28.【答案】B
【解析】选项A,是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,是轴对称图形。
故答案为:B。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
29.【答案】C
【解析】解:680÷8=85,商的末尾没有0。
故答案为:C。
【分析】三位数除以一位数,从被除数的最高位除起,用一位数试除被除数的前一位数,如果它比除数小就试除前两位数,除到哪一位就把商写在那一位上面,每次除后余数要比除数小。除到商的最高位后面哪一位上不够商1要商0。
30.【答案】C
【解析】解:下边的竖式中虚线框内的计算过程表示:每箱装20个,装了60个,余10个。
故答案为:C。
【分析】观察虚线框内的计算过程,在十位上商2,表示每箱装20个,计算后是6,所以表示装60个,余数是1,表示余10个。
31.【答案】D
32.【答案】6×12=72 25×3=75 60×70=4200 10×73=730
42÷3=14 9×800=7200 13×40=520 10-10÷2=5
50×40=2000 560÷8=70 80×25=2000 80+90=170
【解析】因数末尾有0的乘法的计算方法:在计算因数末尾有0的乘法时,可以先把0前面的数相乘,然后看两个因数的末尾一共有几个0,就在积的末尾添上几个0。
除数是一位数的计算方法:1、从被除数的高位起,先用除数试除被除数的前一位数,如果它比除数小,再试除前两位数。2、除到被除数的哪一位,就在那一位上面写商。3、每求出一位商,余下的数必须比除数小。
33.【答案】35;412;289
34.【答案】4872;5.3;102;118……1
35.【答案】(1)解:8+5=13(厘米)
14×13=182(平方厘米)
8×8=64(平方厘米)
182+64=246(平方厘米)
(2)解:7×3=21(厘米)
21×14=294(平方厘米)
14-7=7(厘米)
7×7×2=98(平方厘米)
294-98=196(平方厘米)
【解析】(1)长方形面积=长×宽,正方形面积=边长×边长,用左边长方形面积加上右边正方形面积就是图形的总面积;
(2)用大长方形面积减去空白部分的面积就是图形的面积。空白部分相当于两个边长7厘米的正方形面积。
36.【答案】解:
【解析】补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点或关键线段的对称线段,然后再连线;
做平移后的图形:先把图形中的关键点或关键线段都按题干要求的方向和格数移动,然后再连接各点;据此做图。
37.【答案】解:
1--=
答:还剩全部库存的 没有售出。
【解析】用第一天销售的分率减去第二天比第一天少卖的分率求出第二天卖出的分率。用1减去第一天和第二天卖出的分率求出没有售出的分率。
38.【答案】解:1t=1000kg
1000÷10×1.55
=100×1.55
=155(kg)
答:1t黄豆含有155千克膳食纤维。
【解析】先统一单位:1t=1000kg,大单位转化成小单位乘进率;再根据题意可得:黄豆总数量÷10千克黄豆=1t里面有几个10千克,黄豆总数量÷10千克黄豆×每10千克里面含有的膳食纤维质量=1t黄豆里面含有的膳食纤维质量。
39.【答案】(1)7.98平方米
(2)14米
(3)花坛面积大
(4)319.2克
40.【答案】够
41.【答案】解:35×12=420(人)
414+12=426(人)
420<426
答:租12辆大巴不够。
【解析】租12辆大巴可以坐的人数=平均每辆车限乘的人数×车的辆数,然后和老师人数与学生人数的和比较大小。
42.【答案】解:39×16=624(元)
600元<624元
答:李老师带的钱不够。
【解析】用每付乒乓球拍的钱数乘16求出需要的总钱数,然后与600比较后判断够不够。
43.【答案】李叔叔
44.【答案】(1)解:2×2×300
=4×300
=1200(平方分米)
1200平方分米=12平方米
答:厨房地面的面积是12平方米。
(2)解:1200÷(3×2)
=1200÷6
=200(块)
答:方案二要用200块地砖。
(3)解:300×3=900(元)
200×4=800(元)
900>800
答:方案二便宜。
【解析】(1)厨房地面的面积=方案一地砖的边长×边长×需要地砖的块数,然后单位换算;
(2)方案二要用地砖的块数= 厨房地面的面积÷(方案二地砖的长×宽);
(3)总价=单价×用的块数,然后再比较大小。
45.【答案】解:9米=90分米,6米=60分米
(90÷3)×(60÷3)
=30×20
=600(块)
答:一共要用600块这样的地砖。
【解析】先将长和宽的单位换算成分米,然后求出长方形的长能放几个正方形的边长,宽能放几个正方形的边长,再相乘,即可求出一共要用多少块地砖。
46.【答案】解:方案一:120×4+6×50
=480+300
=780(元)
方案二:(4+6)×100
=10×100
=1000(元)
780元<1000元
答:方案一买票比较合算。
【解析】方案一的总价=成人票单价×数量+儿童票单价×数量;方案二的总价=(成人人数+儿童人数)×单价;然后比较总价的大小。
47.【答案】解:可以用列举法:长:48 24 16 12 8宽: 1 2 3 4 6周长分别是:(48+1)×2=98(米)(24+2)×2=52(米)(16+3)×2=38(米)(12+4)×2=32(米)(8+6)×2=28(米)答:爷爷可以围成长8米、宽6米的长方形,最少需要篱笆28米.
【解析】长方形面积=长×宽,由此可以判断出长方形的长和宽分别可以是多少,然后根据长方形周长公式计算出篱笆的长度,判断出围的方法和篱笆最短的长度即可.
48.【答案】解:900÷40=22.5(元)
500÷20=25(元)
22.5<25
300÷40=7(辆)……20(人)
剩下20人租一辆小车,
900×7+500×1=6800(元)
答:租7辆大车和1辆小车最省钱,需要6800元。
【解析】租大车每人花的钱数=一辆大车的租金÷一辆大车可坐的人数,租小车每人花的钱数=一辆小车的租金÷一辆小车可坐的人数,那么租哪种车每人花的钱数少主要就选哪种车,经过计算主要租大车较为合算。所以用总人数除以每辆大车坐的人数,如果余数大于20,那么所得的商加上1就是租大车的辆数,如果余数小于等于20,那么商就是租大车的辆数,然后再租一辆小车即可。
21世纪教育网(www.21cnjy.com)
2024-2025学年三年级下册数学期末全真模拟培优卷(北师大版)
一、填空题
1.等腰三角形、圆都是 图形,等腰三角形有 条对称轴,圆有 条对称轴。
2.老师拿来了一堆糖果,分给同学们。每人分8颗,最后还剩下6颗,如果再拿来18颗,正好可以给每个同学再分2颗。请问:原来共有 颗。
3.根据a×b=480,直接写出下面算式的得数。
a×(b×2)= (a×2)×(b×3)=
(a÷5)×b= (a×10)×(b÷10)=
4.在横线上填上“>”“<”或“=”。
7厘米 70毫米 300秒 3分 360+20 600
36分米 3米 9000克 1吨 46+27 47+26
5.在算式 ÷6=19……△中,余数最大是 ,这时被除数是 。
6.□÷7=15……☆,☆最大是 ,这时□是 。
7.一个长方形花坛的面积是100平方米,如果它的长扩大到原来的5倍,宽不变,扩建后花坛的面积是 平方米。
8.狗大约能活9年,鳄鱼大约能活182年。鳄鱼的寿命大约是狗的 倍。
9.如图,个相同的长方形和个小正方形拼成一个大正方形,已知其中小正方形的面积为平方厘米,大正方形的面积为平方厘米,则其中长方形的长为 厘米,宽 厘米.
10.2022年,北京将主办第24届冬季奥林匹克运动会。24个2022相乘,积的个位数字是 。
11.同学们,本学期老师让大家做荡秋千的活动中,你发现在相同时间内,荡秋千的次数与 有关。
12.小雨、小东、小松三个人进行跳绳比赛.小松说:“我不是最后一名.”小东说:“我也不是最后一名,但小松的成绩比我好.”那么 是第一名, 是最后一名.
二、判断题
13.周长相等的两个长方形面积一定相等。( )
14.计算25×30时,可以先算出25×3=75,再在末尾加一个0。( )
15.两位数乘两位数:□5×□8,积的末尾只有一个0。( )
16.拉抽屉时抽屉的运动是平移。( )
17.三位数除以一位数商可能是两位数。(
)
18.小芳用一周的时间把一本书看完了,每天看的页数相同,那么3天她看了全书的。( )
19.周长相等的两个正方形,它们的面积一定相等。( )
三、单选题
20.与1吨最接近的是( )。
A.999克 B.9千克 C.990千克 D.1001克
21.要使 89÷5的商是两位数, 里可以填( )。
A.6~9 B.0~4 C.1~4
22.有两个同样大小的杯子,里面都倒满了牛奶,欣欣喝了这杯牛奶的 ,小雨喝了这杯牛奶的 ,( )剩下的牛奶多。
A.欣欣 B.小雨 C.一样多
23.把2盒饼干平均分给6个小朋友,其中4个小朋友分得这些饼干的( )。
A. B. C.
24.下图可以看作是一个等腰直角三角形旋转若干次后形成的,每次旋转的度数是( )。
A.90° B.60° C.45° D.30°
25.一个长方形的长和一个正方形的边长相等,它的面积( )。
A.长方形比正方形大
B.长方形比正方形小
C.长方形和正方形相等
26.一条公路七天修完了 ,三天修了这条路的( )
A. B. C. D.
27.利用数学知识进行分析,下列叙述合理的是( )。
A.课桌的高度是20分米 B.正常成年人步行速度为每分钟60米
C.一个西瓜重100千克 D.一个保温杯的容积是500L
28.下列各图案中不是轴对称是( )。
A. B. C. D.
29.680÷8商末尾的0有( )。
A.3个 B.2个 C.0个
30.把74个苹果平均装入3个箱子,每个箱子装几个苹果 下边的竖式中虚线框内的计算过程表示( )。
A.每箱装2个,装了6个,余1个
B.每箱装20个,装了60个,余1个
C.每箱装20个,装了60个,余10个
31.有一块面积是240m2、宽是8m的长方形绿地。长不变,宽增加了24m,求扩大后的面积是多少平方米。下面能正确表示题中数量关系的是( )。
A. B.
C. D.
四、计算题
32.口算
6×12= 25×3= 60×70= 10×73=
42÷3= 9×800= 13×40= 10-10÷2=
50×40= 560÷8= 80×25=
80+90=
33.递等式计算。
(83+57)÷4 244+6×28 352-(152-89)
34.列竖式计算。(带★的要验算)
58×84= ★10-4.7= 918÷9= ★709÷6=
35.计算下面图形的面积。(单位:厘米)
(1)
五、作图题
36.请按照要求作图。
①先根据对称轴,画出对称图形的另一半。
②画出这个轴对称图形先向上平移2格,再向右平移4格后的图形。
六、解决问题
37.对农直播电商结合直播技术和农产品销售,实现了农村经济的增长和农民的增收。某直播间第一天销售了红薯库存的 ,第二天比第一天少卖全部库存的 ,则还剩全部库存的几分之几没有售出?
38.黄豆的营养价值很高, 10kg黄豆含3.5kg蛋白质、1.55kg膳食纤维、1.6kg脂肪、1.87kg碳水化合物,另含有许多微量元素。照这样计算,lt黄豆含有多少千克膳食纤维?
39.学校有一块长方形草坪和一个正方形花坛,如图。
(1)草坪的面积是多少?
(2)如果给花坛四周围上篱笆,需要多长的篱笆?
(3)比一比,花坛和草坪,谁的面积大?
(4)如果草坪每平方米每天大的可吸收40克二氧化碳,这块草坪每天可吸收多少克二氧化碳?
40.王老师带着36名同学去儿童乐园,带了500元,够买门票够吗?
41.佛山大剧院是佛山新城文化艺术中心的核心组成部分,位于佛山市文化中心坊塔内东侧。为促进学生全面发展,增强学生体质健康,学期结束,伴着明媚阳光和雀跃的心情,实验小学三年级学生在老师的带领下,前往佛山市文化中心,开展一次有意义的综合社会实践活动。实验小学9个班共414名同学,由12位老师带领乘大巴前往目的地,一辆大巴可以坐35人,租12辆大巴够吗?
42.益民商店每付乒乓球拍39元,李老师准备给学校乒乓球队买16付乒乓球拍,他带了600元钱,李老师带的钱够吗?
43.社区宣传员在向社区居民做“防网络诈骗”宣传工作,安排了一些工作人员向居民发放宣传单。张阿姨7分钟发了266张,李叔叔4分钟发了156张。他们两人中,谁平均每分钟发放的宣传单多?
44.王老师计划给他家的厨房铺地砖,他设计了两种方案。(对应作业目标:3507,3508)
方案一:用边长是2分米的正方形地砖,每块地砖3元。
方案二:用长3分米、宽2分米的长方形地砖,每块地砖4元。
(1)方案一要用300块地砖。厨房地面的面积是多少平方米
(2)方案二要用多少块地砖
(3)哪种方案便宜
45.学校会议室的地面是长方形,长9米,宽6米。用边长3分米的正方形地砖铺满这间会议室的地面,一共要用多少块这样的地砖?
46.金山旅行社推出“莲花山景区一日游”的两种出游价格方案。成人4人,儿童6人,选哪个方案买票比较合算?请通过计算简单说明理由。
方案一:成人120元/人,儿童50元/人;
方案二:团体10人以上(包含10人),100元/人。
47.爷爷想围一个面积48平方米的长方形鸡圈,爷爷可以怎样围?最少需要篱笆长多少米?(长和宽都取整米数)
48.300名同学去春游,怎样租车最省钱?
参考答案及试题解析
1.【答案】轴对称;1;无数
【解析】等腰三角形、圆都是轴对称图形,等腰三角形有1条对称轴,圆有无数条对称轴。
故答案为:轴对称;1;无数。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
2.【答案】102
【解析】解:同学人数:(18+6)÷2=12(人),
原来树苗数量:
8×12+6
=96+6
=102(棵),
答:原来共有102棵树苗。
故答案为:102
【分析】 由题意,每人分8棵树苗,最后还剩下6棵,如果再拿来18棵,正好可以给每个同学再分2棵,即每人多分给2棵,就多分了(6+18)棵,由此可求得共有多少个同学,进而求得原来共有多少棵树苗.
3.【答案】960;2880;96;480
【解析】解:a×(b×2)=960;(a×2)×(b×3)=2880
(a÷5)×b=96;(a×10)×(b÷10)=480。
故答案为:960;2880;96;480。
【分析】两个数相乘,一个乘数不变,另一个乘数扩大或缩小多少倍(0除外),积就扩大或缩小相同的倍数。两个数相乘,一个乘数扩大或缩小多少倍(0除外),另一个乘数缩小或扩大相同的倍数,积不变。
4.【答案】=;>;<;>;<;=
【解析】7厘米=70毫米;
因为3分=180秒,300秒>180秒,所以300秒>3分;
因为360+20=380,380<600,所以360+20<600;
因为3米=30分米,36分米>30分米,所以36分米>3米;
因为1吨=1000千克=1000000克,9000克<1000000克,所以9000克<1吨;
因为46+27=73,47+26=73,所以46+27=47+26。
故答案为:=;>;<;>;<;=。
【分析】根据1厘米=10毫米,1分=60秒,1米=10分米,1吨=1000千克,1千克=1000克,将单位化统一,再比较大小;
比较两个算式的大小,先分别计算出得数,再比较大小。
5.【答案】5;119
【解析】解:在算式 ÷6=19……△中,余数最大是5,
这时被除数=19×6+5
=114+5
=119。
故答案为:5;119。
【分析】在有余数的除法算式中,余数一定比除数小,所以除数已知时,余数最大=除数-1,再根据被除数=商×除数+1计算即可得出答案。
6.【答案】6;111
7.【答案】500
【解析】解:100×5=500(平方米),
所以扩建后花坛的面积是500平方米。
故答案为:500。
【分析】长方形的面积=长×宽,积的变化规律:一个因数不变,另一个因数扩大几倍(倍数不为0),积就扩大几倍,本题中扩建后的面积=扩大前的面积×长扩大的倍数,代入数值计算即可。
8.【答案】20
【解析】解:182÷9=20。
故答案为:20。
【分析】鳄鱼的寿命大约是狗寿命的倍数=鳄鱼的寿命÷狗的寿命。
9.【答案】11;9
【解析】解:400=20×20
所以大正方形的边长是20厘米;
4=2×2
所以小正方形的边长是2厘米;
(20-2)÷2
=18÷2
=9(厘米)
(400-4)÷4÷9
=396÷4÷9
=99÷9
=11(厘米);
答:长方形的长是11厘米.宽是9厘米.
故答案为:11,9.
【分析】大正方形面积是400平方厘米,边长应是20厘米;小正方形面积是4平方厘米,边长应是2厘米;大正方形边长减去小正方形边长正好等于长方形的两个宽,所以长方形的宽应是(20-2)÷2=9(厘米);根据“长方形的长=面积÷宽”,代入数值进行解答即可.
10.【答案】6
【解析】解:2=2,个位是2
2×2=4,个位是4
2×2×2=8,个位是8
2×2×2×2=16,个位是6
2×2×2×2×2=32,个位是2
2×2×2×2×2×2=64,个位是4
……
即每4个2相乘,积的个位就会出现循环;
24÷4=6....0
则24个2相乘,积的个位数字是与每组的第4个数字相同,即6。
故答案为:6。
【分析】根据题意,2022的个位是2,其积的个位数字只与2有关;从n个2相乘所得积的个位数字寻找规律,发现每4个2相乘,积的个位就会出现循环,用24÷4发现余数为0,说明个位数字是每个循环里最后一个数,即6。
11.【答案】绳子长短
【解析】解:在相同时间内,荡秋千的次数与物体质量无关,与绳子长短有关。
故答案为:绳子长短。
【分析】在相同时间内,同一个秋千(摆长不变),荡的次数是不变的,而且与质量无关,绳子的长度越长,周期越大,频率越小,所以次数就变小,据此解答即可。
12.【答案】小松;小雨
【解析】根据题意,由小松和小东都不是最后一名可知,小雨是最后一名;
由小东说小松的成绩比他好可知,小松是第一名。所以:小松是第一名,小雨是最后一名。
故答案为:小松;小雨。
【分析】小松说:“我不是最后一名。”小东说:“我也不是最后一名。”所以小雨是最后一名,又因为小东说:“小松的成绩比我好.”所以小松是第一名。
13.【答案】错误
【解析】解:周长相等的两个长方形面积不一定相等。
故答案为:错误。
【分析】其中一个长方形的长和宽分别是4和2,那么它的周长是(4+2)×2=12,面积是4×2=8;另一个长方形的长和宽分别是5和1,那么它的周长是(5+1)×2=12,面积是5×1=5,所以它们周长相等但是面积不相等。
14.【答案】正确
15.【答案】错误
【解析】解:如:25×48=1200,积的末尾有2个0;
15×28=420,积的末尾只有一个0,所以原题干说法错误。
故答案为:错误。
【分析】两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
16.【答案】正确
【解析】根据平移的基本知识,拉抽屉时抽屉的运动是平移,只发生了位置变动,大小不变。
【分析】考查基本的平移知识
17.【答案】正确
【解析】解:三位数除以一位数商可能是两位数,也可能的三位数。
故答案为:正确。
【分析】三位数除以一位数,如果被除数百位上的数字大于或等于除数,商是三位数;如果被除数百位上的数字小于除数,商是两位数。
18.【答案】错误
【解析】解:++
=+
=。
故答案为:错误。
【分析】一周是7天,小芳用一周的时间把一本书看完了,并且每天看的页数相同,则她每天看全书的,3天她看了全书的。
19.【答案】正确
【解析】解:周长相等的两个正方形,它们的面积一定相等,原题干说法正确。
故答案为:正确。
【分析】正方形的面积=边长×边长,周长相等的两个正方形,边长=周长÷4,边长相等,则它们的面积一定相等。
20.【答案】C
【解析】与1吨最接近的是990千克。
故答案为:C。
【分析】根据1吨=1000千克,对比各选项的数,即可得到最接近1吨的数,据此解答。
21.【答案】C
【解析】解:里可以填1~4中任何一个数。
故答案为:C。
【分析】三位数除以一位数,如果首位够除,那么商是三位数,如果首位不够除,那么商是两位数。
22.【答案】B
【解析】解:,因为小雨喝的少,所以剩下的就多。
故答案为:B。
【分析】有两个同样大小的杯子,里面都倒满了牛奶,喝的少的,剩下的就多。
23.【答案】A
【解析】解:4÷6=。
故答案为:A。
【分析】4个小朋友分得这些饼干的分率=4÷平均分给小朋友的人数。
24.【答案】C
【解析】等腰直角三角形的一个直角是90度,另外两个底角是45度,所以可以看作是一个等腰直角三角形每次旋转的45度后形成的。
故答案为:C。
【分析】在旋转时,旋转中心不变,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角。这个图中的旋转角正好是等腰直角三角形的一个底角。
25.【答案】B
【解析】解:长方形的面积比正方形的面积小。
故答案为:B。
【分析】长方形的面积=长×宽,正方形的面积=边长×边长,因为长方形的长和正方形的边长相等,长方形的宽小于正方形的边长,所以长方形的面积比正方形的面积小。
26.【答案】B
【解析】解:三天修了这条路的。
故答案为:B。
【分析】每天修了这条路的,那么3天修了这条路的。
27.【答案】B
28.【答案】B
【解析】选项A,是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,是轴对称图形。
故答案为:B。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
29.【答案】C
【解析】解:680÷8=85,商的末尾没有0。
故答案为:C。
【分析】三位数除以一位数,从被除数的最高位除起,用一位数试除被除数的前一位数,如果它比除数小就试除前两位数,除到哪一位就把商写在那一位上面,每次除后余数要比除数小。除到商的最高位后面哪一位上不够商1要商0。
30.【答案】C
【解析】解:下边的竖式中虚线框内的计算过程表示:每箱装20个,装了60个,余10个。
故答案为:C。
【分析】观察虚线框内的计算过程,在十位上商2,表示每箱装20个,计算后是6,所以表示装60个,余数是1,表示余10个。
31.【答案】D
32.【答案】6×12=72 25×3=75 60×70=4200 10×73=730
42÷3=14 9×800=7200 13×40=520 10-10÷2=5
50×40=2000 560÷8=70 80×25=2000 80+90=170
【解析】因数末尾有0的乘法的计算方法:在计算因数末尾有0的乘法时,可以先把0前面的数相乘,然后看两个因数的末尾一共有几个0,就在积的末尾添上几个0。
除数是一位数的计算方法:1、从被除数的高位起,先用除数试除被除数的前一位数,如果它比除数小,再试除前两位数。2、除到被除数的哪一位,就在那一位上面写商。3、每求出一位商,余下的数必须比除数小。
33.【答案】35;412;289
34.【答案】4872;5.3;102;118……1
35.【答案】(1)解:8+5=13(厘米)
14×13=182(平方厘米)
8×8=64(平方厘米)
182+64=246(平方厘米)
(2)解:7×3=21(厘米)
21×14=294(平方厘米)
14-7=7(厘米)
7×7×2=98(平方厘米)
294-98=196(平方厘米)
【解析】(1)长方形面积=长×宽,正方形面积=边长×边长,用左边长方形面积加上右边正方形面积就是图形的总面积;
(2)用大长方形面积减去空白部分的面积就是图形的面积。空白部分相当于两个边长7厘米的正方形面积。
36.【答案】解:
【解析】补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点或关键线段的对称线段,然后再连线;
做平移后的图形:先把图形中的关键点或关键线段都按题干要求的方向和格数移动,然后再连接各点;据此做图。
37.【答案】解:
1--=
答:还剩全部库存的 没有售出。
【解析】用第一天销售的分率减去第二天比第一天少卖的分率求出第二天卖出的分率。用1减去第一天和第二天卖出的分率求出没有售出的分率。
38.【答案】解:1t=1000kg
1000÷10×1.55
=100×1.55
=155(kg)
答:1t黄豆含有155千克膳食纤维。
【解析】先统一单位:1t=1000kg,大单位转化成小单位乘进率;再根据题意可得:黄豆总数量÷10千克黄豆=1t里面有几个10千克,黄豆总数量÷10千克黄豆×每10千克里面含有的膳食纤维质量=1t黄豆里面含有的膳食纤维质量。
39.【答案】(1)7.98平方米
(2)14米
(3)花坛面积大
(4)319.2克
40.【答案】够
41.【答案】解:35×12=420(人)
414+12=426(人)
420<426
答:租12辆大巴不够。
【解析】租12辆大巴可以坐的人数=平均每辆车限乘的人数×车的辆数,然后和老师人数与学生人数的和比较大小。
42.【答案】解:39×16=624(元)
600元<624元
答:李老师带的钱不够。
【解析】用每付乒乓球拍的钱数乘16求出需要的总钱数,然后与600比较后判断够不够。
43.【答案】李叔叔
44.【答案】(1)解:2×2×300
=4×300
=1200(平方分米)
1200平方分米=12平方米
答:厨房地面的面积是12平方米。
(2)解:1200÷(3×2)
=1200÷6
=200(块)
答:方案二要用200块地砖。
(3)解:300×3=900(元)
200×4=800(元)
900>800
答:方案二便宜。
【解析】(1)厨房地面的面积=方案一地砖的边长×边长×需要地砖的块数,然后单位换算;
(2)方案二要用地砖的块数= 厨房地面的面积÷(方案二地砖的长×宽);
(3)总价=单价×用的块数,然后再比较大小。
45.【答案】解:9米=90分米,6米=60分米
(90÷3)×(60÷3)
=30×20
=600(块)
答:一共要用600块这样的地砖。
【解析】先将长和宽的单位换算成分米,然后求出长方形的长能放几个正方形的边长,宽能放几个正方形的边长,再相乘,即可求出一共要用多少块地砖。
46.【答案】解:方案一:120×4+6×50
=480+300
=780(元)
方案二:(4+6)×100
=10×100
=1000(元)
780元<1000元
答:方案一买票比较合算。
【解析】方案一的总价=成人票单价×数量+儿童票单价×数量;方案二的总价=(成人人数+儿童人数)×单价;然后比较总价的大小。
47.【答案】解:可以用列举法:长:48 24 16 12 8宽: 1 2 3 4 6周长分别是:(48+1)×2=98(米)(24+2)×2=52(米)(16+3)×2=38(米)(12+4)×2=32(米)(8+6)×2=28(米)答:爷爷可以围成长8米、宽6米的长方形,最少需要篱笆28米.
【解析】长方形面积=长×宽,由此可以判断出长方形的长和宽分别可以是多少,然后根据长方形周长公式计算出篱笆的长度,判断出围的方法和篱笆最短的长度即可.
48.【答案】解:900÷40=22.5(元)
500÷20=25(元)
22.5<25
300÷40=7(辆)……20(人)
剩下20人租一辆小车,
900×7+500×1=6800(元)
答:租7辆大车和1辆小车最省钱,需要6800元。
【解析】租大车每人花的钱数=一辆大车的租金÷一辆大车可坐的人数,租小车每人花的钱数=一辆小车的租金÷一辆小车可坐的人数,那么租哪种车每人花的钱数少主要就选哪种车,经过计算主要租大车较为合算。所以用总人数除以每辆大车坐的人数,如果余数大于20,那么所得的商加上1就是租大车的辆数,如果余数小于等于20,那么商就是租大车的辆数,然后再租一辆小车即可。
21世纪教育网(www.21cnjy.com)
同课章节目录
