北师大版五年级数学下册期末考试综合素养测评检测卷一(含解析)
文档属性
| 名称 | 北师大版五年级数学下册期末考试综合素养测评检测卷一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 487.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 18:03:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版五年级数学下册期末考试综合素养测评检测卷一
一、填空题(共20分)
1.(2分)在讲故事比赛中,7位评委给丽丽的打分数分别是9.9分、10分、8.5分、9.6分、9.5分、9.3分、9.2分,7位评委给丽丽的平均分是( )分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是( )分。(除不尽保留一位小数)
2.(2分)小狗站在百米跑道的终点,看到起点有一个像是它主人的人向它走来。它盯着看了5秒,确定那就是主人,于是它以3米/秒的速度向主人跑去,若主人的行走速度是2米/秒,则小狗跑了( )秒和主人相遇。
3.(2分)如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
4.(2分)下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的( )方向上,孙刘联军在曹军的( )方向上。
5.(2分)鸡的孵化期是21天,鸭的孵化期是鸡的,鸭的孵化期是( )天;鸭的孵化期是鹅的孵化期的,鹅的孵化期是( )天。
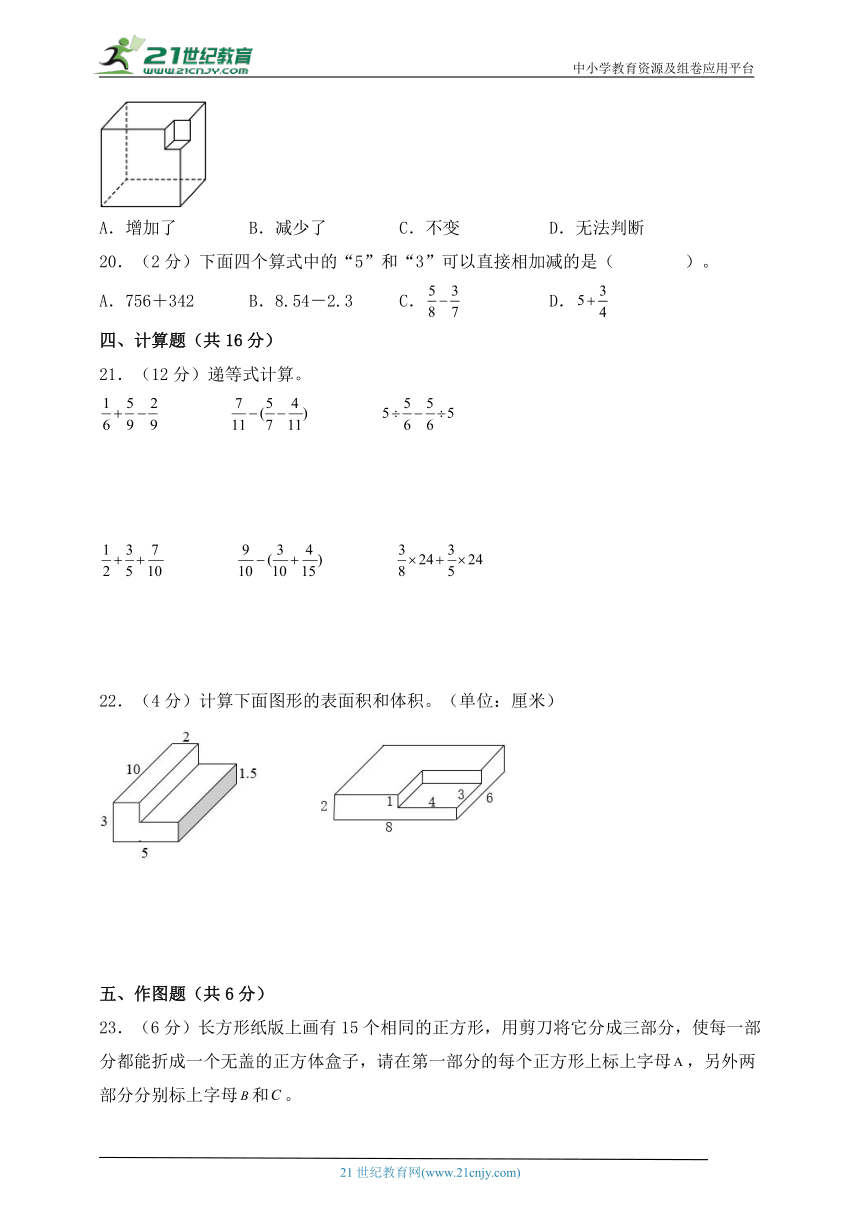
6.(2分)一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是( )cm2。体积是( )cm3。
7.(2分)小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了( )页,还剩( )页。
8.(2分)苗圃中的一些苗木很珍贵,园艺工人买了一根20m长的绳子将一些珍贵的苗木保护起来,捆绑沉香苗用去,捆绑一棵紫檀苗用去了m,还剩下绳子( )m。
9.(2分)做一个长8厘米、宽和高都是5厘米的长方体框架,需要( )厘米长的塑料棒,现在外面糊上彩纸,至少需要( )平方厘米的彩纸(接头处忽略不计)。
10.(2分)(小数)。
二、判断题(共10分)
11.(2分)小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。( )
12.(2分)把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
13.(2分)长方形的长是米,宽是米,则它的面积是平方米。( )
14.(2分)3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。( )
15.(2分)动物学校举行了一场运动会,在500米比赛中,小黄狗用了0.62分,小兔子用了分,小黄狗跑得快。( )
三、选择题(共10分)
16.(2分)一列火车长304米,它的速度是每小时126千米,一个骑车人与火车相向而行,全列火车从他身边开过用8秒钟。这个骑车人的速度是每小时( )千米。
A.8 B.10 C.10.2 D.10.8 E.12.6
17.(2分)一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向( )。
A.南偏西30°方向飞行800千米 B.西偏南30°方向飞行800千米
C.北偏东30°方向飞行800千米 D.东偏北30°方向飞行800千米
18.(2分)下列各组数中,互为倒数的是( )。
A.和 B.和 C.和 D.0.5和
19.(2分)在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,( )。
A.增加了 B.减少了 C.不变 D.无法判断
20.(2分)下面四个算式中的“5”和“3”可以直接相加减的是( )。
A.756+342 B.8.54-2.3 C. D.
四、计算题(共16分)
21.(12分)递等式计算。
22.(4分)计算下面图形的表面积和体积。(单位:厘米)
五、作图题(共6分)
23.(6分)长方形纸版上画有15个相同的正方形,用剪刀将它分成三部分,使每一部分都能折成一个无盖的正方体盒子,请在第一部分的每个正方形上标上字母,另外两部分分别标上字母和。
六、解答题(共38分)
24.(4分)“双减”政策实施后,小轩监督自己的学习情况,每次做完《黄冈名师》里的单元卷都要给自己批改出成绩。在11次的数学测评中平均成绩是91分。在临近期末的最后这次测评成绩出来后,他发现这一次的成绩比这12次测评的平均成绩高5.5分,小轩在第12次测评中得了多少分?
25.(4分)政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
26.(4分)甲、乙、丙三位志愿者在一次救灾募捐中积极捐款,乙的捐款数比甲的2倍少100元,丙的捐款数比甲、乙两人的捐款数的和少300元,甲的捐款数是丙的,那么甲捐款多少元?
27.(4分)小亮做测量“石块体积”的实验,他先将一块棱长是6厘米的正方体铁块浸没在一个长方体水槽中,然后取出正方体铁块,水槽里边的水面下降了2厘米。接着,他把要测量的一个石块浸没在水槽中,这时,水槽里的水面上升了1.5厘米。这个石块的体积是多少立?
28.(4分)创卫工作人人有责,爱护环境从我做起。阳光小学组织六年级同学参加创卫活动,共收集了500个易拉罐。六(1)班收集的数量占总数量的,六(1)班男生收集的数量占本班收集数量的,六(1)班女生共收集了多少个易拉罐?
29.(4分)如下图,把一个长方体木块正好锯成三个大小相等的小正方体,它们的表面积的和比原来长方体表面积增加了36平方厘米,原来长方体的表面积是多少平方厘米?
30.(4分)有两袋苹果,第一袋质量为千克,如果从第一袋中取出千克放入第二袋中,那么两袋苹果一样重。原来两袋苹果共有多少千克?
31.(10分)下图是某出租车司机2022年下半年收入、支出情况统计图。
月份 7月 8月 9月 10月 11月 12月
收入/万元 0.9 0.2 0.1 0.6 1.3 1.4
支出/万元 0.4 0.3 0.2 0.4 0.6 0.5
(1)根据上面的表格,完成下面的统计图。
(2)该出租车司机2022年下半年( )月份利润最大,是( )万元。(利润=收入-支出)
(3)该出租车司机2022年下半年平均每月的支出是( )万元。
(4)该出租车司机2022年8月份的收入是10月收入的( )。(填最简分数)
答案解析
一、填空题(共20分)
1.(2分)在讲故事比赛中,7位评委给丽丽的打分数分别是9.9分、10分、8.5分、9.6分、9.5分、9.3分、9.2分,7位评委给丽丽的平均分是( )分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是( )分。(除不尽保留一位小数)
【答案】 9.4 9.5
【分析】根据平均数=总数量÷总份数,求出7位评委给丽丽的平均分;去掉最高分和最低分后,再根据平均数的求法,计算出丽丽的平均得分。保留一位小数看百分位,小于5直接舍去,大于或等于5向前一位进一。
【解答】(9.9+10+8.5+9.6+9.5+9.3+9.2)÷7
=66÷7
≈9.4(分)
(9.9+9.6+9.5+9.3+9.2)÷5
=47.5÷5
=9.5(分)
7位评委给丽丽的平均分是9.4分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是9.5分。
2.(2分)小狗站在百米跑道的终点,看到起点有一个像是它主人的人向它走来。它盯着看了5秒,确定那就是主人,于是它以3米/秒的速度向主人跑去,若主人的行走速度是2米/秒,则小狗跑了( )秒和主人相遇。
【答案】18
【分析】设小狗跑了秒和主人相遇。根据等量关系:100米=小狗秒跑的路程+主人秒行的路程+主人5秒行的路程,列出方程即可求解。
【解答】解:设小狗跑了秒和主人相遇。
3+2+2×5=100
3+2+10=100
5+10=100
5+10-10=100-10
5=90
5÷5=90÷5
=18
小狗跑了18秒和主人相遇。
3.(2分)如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
【答案】 (2a+1) 15
【分析】探究摆a个三角形所需小棒数量规律:
从简单情形入手:摆1个三角形,直接可知需要3根小棒。
分析数量递增关系:摆2个三角形时,第二个三角形与第一个三角形共用1条边,所以相比摆1个三角形,只多了2根小棒,总共用3+2=5根小棒;摆3个三角形时,第三个三角形与前面图形共用1条边,相比摆2个三角形又多了2根小棒,即5+2=7根小棒。依此类推,每增加1个三角形,就增加2根小棒。
推导通用表达式:摆a个三角形,第一个三角形用3根小棒,后面(a-1)个三角形每个都增加2根小棒,所以总共需要小棒数为3+2×(a-1)根。对其化简:
已知摆a个三角形需要2a+1根小棒,现有31根小棒,可据此列出式子2a+1=31,求出三角形的个数。
【解答】摆a个△所需小棒数:
3+2×(a-1)
=3+2a-2
=(2a+1)个
求31根小棒能摆△的个数设31根小棒能摆a个△,则2a+1=31。
2a+1=31
解:2a+1-1=31-1
2a=30a
a=30÷2
a=15
综上,摆a个△需要2a+1根小棒,31根小棒可以摆15个△。
4.(2分)下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的( )方向上,孙刘联军在曹军的( )方向上。
【答案】 西偏北30度 东偏南30度
【分析】根据地图上方向:上北下南左西右东,以孙刘联军为观测点,找到曹军的位置,再根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【解答】下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的西偏北30度方向上,孙刘联军在曹军的东偏南30度方向上。
【点评】本题考查根据方向、角度和距离确定物体的位置以及位置的相对性。
5.(2分)鸡的孵化期是21天,鸭的孵化期是鸡的,鸭的孵化期是( )天;鸭的孵化期是鹅的孵化期的,鹅的孵化期是( )天。
【答案】 28 30
【分析】已知鸭的孵化期是鸡的,把鸡的孵化期21天看作单位“1”,单位“1”已知,用鸡的孵化期乘,求出鸭的孵化期;
已知鸭的孵化期是鹅的孵化期的,把鹅的孵化期看作单位“1”,单位“1”未知,用鸭的孵化期除以,求出鹅的孵化期。
【解答】21×=28(天)
28÷
=28×
=30(天)
鸭的孵化期是28天,鹅的孵化期是30天。
6.(2分)一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是( )cm2。体积是( )cm3。
【答案】 504 648
【分析】分析题目,截成的正方体的棱长是6cm,则原来长方体的长是(6×3)cm,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高代入数据列式计算即可。
【解答】6×3=18(cm)
(18×6+18×6+6×6)×2
=(108+108+36)×2
=252×2
=504(cm2)
18×6×6
=108×6
=648(cm3)
一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是504cm2。体积是648cm3。
7.(2分)小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了( )页,还剩( )页。
【答案】 35 70
【分析】把这本数的总页数看作单位“1”,第一天看了全书的,求第一天看的页数,用这本数的总页数×解答;求还剩多少页,用这本数的总页数-第一天小明看的页数,即可解答。
【解答】105×=35(页)
105-35=70(页)
小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了35页,还剩70页。
8.(2分)苗圃中的一些苗木很珍贵,园艺工人买了一根20m长的绳子将一些珍贵的苗木保护起来,捆绑沉香苗用去,捆绑一棵紫檀苗用去了m,还剩下绳子( )m。
【答案】
【分析】由题可知,绳子的总长度是20m,把绳子的总长度看作单位“1”,已知捆绑沉香苗用去,则还剩下(1-),用绳子的总长度乘(1-),求出捆绑沉香苗后剩下的长度,又知捆绑一颗紫檀苗用去了m,再用剩下的绳子长度减去m,即可求出捆绑紫檀苗后剩下的长度。
【解答】20×(1-)-
=20×-
=10-
=(m)
还剩下绳子m。
9.(2分)做一个长8厘米、宽和高都是5厘米的长方体框架,需要( )厘米长的塑料棒,现在外面糊上彩纸,至少需要( )平方厘米的彩纸(接头处忽略不计)。
【答案】 72 210
【分析】求塑料棒的长度就是求棱长总和,因为长方体有4条长,4条宽,4条高;根据“长方体的棱长总和=(长+宽+高)×4”进行解答即可;求需要彩纸的面积,就是求长方体的表面积,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”"进行解答即可。
【解答】(8+5+5)×4
=18×4
=72(厘米)
(8×5+8×5+5×5)×2
=(40+40+25)×2
=105×2
=210(平方厘米)
所以做一个长8厘米、宽和高都是5厘米的长方体框架,需要72厘米长的塑料棒,现在外面糊上彩纸,至少需要210平方厘米的彩纸。
10.(2分)(小数)。
【答案】9;20;40;0.6
【分析】根据分数的基本性质,的分子和分母都乘8就是,的分子和分母都乘3就是;根据分数与除法的关系,=3÷5,根据商不变的规律,3÷5=12÷20;把化成小数是0.6;据此解答。
【解答】=12÷20===0.6
二、判断题(共10分)
11.(2分)小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。( )
【答案】√
【分析】由位置的相对性可知,当观测点相反时,观察到的方向就正好相反,角度不变,南偏东的相反方向是北偏西,据此判断。
【解答】小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。说法正确。
故答案为:√
12.(2分)把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
【答案】√
【分析】把一个长方体切成两个相同的小长方体,因为面数目增加,所以表面积增加,但是体积没变,据此分析。
【解答】
如图,把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变,说法正确。
故答案为:√
13.(2分)长方形的长是米,宽是米,则它的面积是平方米。( )
【答案】√
【分析】长方形面积=长×宽,由此计算出这个长方形的面积即可。
【解答】×=(平方米)
所以,长方形的面积是平方米。
故答案为:√
14.(2分)3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。( )
【答案】√
【分析】从正面看有3个面露在外面,从上面看有2个面露在外面,从右边看有2个面露在外面,一共有3+2+2个面露在外面,再根据正方形面积公式:面积=边长×边长,求出一个正方体的面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,再进行比较,即可解答。
【解答】2×2×(3+2+2)
=4×(5+2)
=4×7
=28(cm2)
3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。
原题干说法正确。
故答案为:√
【点评】解答本题的关键是求出露在外面的个数。
15.(2分)动物学校举行了一场运动会,在500米比赛中,小黄狗用了0.62分,小兔子用了分,小黄狗跑得快。( )
【答案】√
【分析】同样的距离,时间越少速度越快,据此比较小黄狗和小兔子用的时间即可。小数与分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【解答】=16÷25=0.64
0.62<,小黄狗跑得快,说法正确。
故答案为:√
三、选择题(共10分)
16.(2分)一列火车长304米,它的速度是每小时126千米,一个骑车人与火车相向而行,全列火车从他身边开过用8秒钟。这个骑车人的速度是每小时( )千米。
A.8 B.10 C.10.2 D.10.8 E.12.6
【答案】D
【分析】根据速度和=总路程÷时间,先用304除以8求出两者的速度和,然后转化单位,再减去火车的速度即可。
【解答】304÷8=38(米/秒)
38米/秒=136.8千米/小时
136.8﹣126=10.8(千米/小时)
所以这个骑车人的速度是每小时10.8千米。
故答案选:D
17.(2分)一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向( )。
A.南偏西30°方向飞行800千米 B.西偏南30°方向飞行800千米
C.北偏东30°方向飞行800千米 D.东偏北30°方向飞行800千米
【答案】D
【分析】一架飞机从某机场向南偏西60°方向飞行了800千米,原路返回时飞机飞行的距离不变,与来时的方向完全相反,偏的角度不变。据此解答即可。
【解答】一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向北偏东60°方向或东偏北30°方向,飞行800千米。
故答案为:D
【点评】方向是相对的,以点A的位置为观测点看点B与以点B的位置为观测点点A,方向完全相反,所偏的度数及距离不变。
18.(2分)下列各组数中,互为倒数的是( )。
A.和 B.和 C.和 D.0.5和
【答案】B
【分析】乘积是1的两个数互为倒数。据此分别计算各选项中两个数的乘积即可解答。
【解答】A.×=,则和不互为倒数;
B.×=1,则和互为倒数;
C.×=,则和不互为倒数;
D.0.5×=,则0.5和不互为倒数。
故答案为:B
19.(2分)在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,( )。
A.增加了 B.减少了 C.不变 D.无法判断
【答案】C
【分析】原来大正方体的表面积需要计算小长方体上面、正面、右面的面积,挖掉小长方体后剩下物体的表面积需要计算小长方体下面、后面、左面的面积,其余部分面积不变,小长方体相对的面完全相同,则表面积不变;据此选择。
【解答】由分析可得:在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,不变。
故答案为:C
20.(2分)下面四个算式中的“5”和“3”可以直接相加减的是( )。
A.756+342 B.8.54-2.3 C. D.
【答案】B
【分析】计算整数和小数的加减法,相同数位要对齐,即计数单位相同的数才能相加减。异分母分数相加减,先通分,化成同分母分数,再相加减,即分数单位相同的分数,才能把分子相加减。
【解答】A.756中5在十位上,表示5个十,342中3在百位上,表示3个百,计数单位不同,不能直接相加。
B.8.54中5在十分位上,表示5个0.1,2.3中3在十分位上,表示3个0.1,计数单位相同,能直接相加。
C.的分数单位是,表示5个,的分数单位是,表示3个,分数单位不同,不能直接相减
D.5表示5个一,的分数单位是,表示3个,计数单位不同,不能直接相加。
故答案为:B
四、计算题(共16分)
21.(12分)递等式计算。
【答案】;;5
;;23.4
【分析】(1)运用加法的结合律进行简算;
(2)运用减法的性质、加法的交换律进行简算;
(3)先算除法,再算减法;
(4)直接约分进行计算;
(5)运用减法的性质进行简算;
(6)先算乘法,再算加法。
【解答】(1)
=
=
=
(2)
=
=
=1-
=
(3)
=6-
=5
(4)
=
=
=
(5)
=
=
=
(6)
=9+14.4
=23.4
22.(4分)计算下面图形的表面积和体积。(单位:厘米)
【答案】左图:190平方厘米;105立方厘米
右图:152平方厘米;84立方厘米
【分析】左图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为10厘米,宽5厘米,高3厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立体图形的体积,可以看作两个长方体的体积,一个是下面的扁一点的长方体,该长方体长为10厘米,宽为5厘米,高为1.5厘米,另外一个长方体是在上方的稍微小一点的长方体,该长方体长为10厘米,宽为2厘米,高为(3-1.5)厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
右图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为8厘米,宽6厘米,高2厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立方体的体积,可以看作大的长方体的体积减去一个小长方体体积,小长方体长为4厘米,宽为3厘米,高为1厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
【解答】由分析可得:
左面图形表面积:
(10×5+10×3+3×5)×2
=(50+30+15)×2
=(80+15)×2
=95×2
=190(平方厘米)
左面图形体积:
10×5×1.5+10×2×(3-1.5)
=50×1.5+10×2×1.5
=75+20×1.5
=75+30
=105(立方厘米)
右面图形表面积:
(8×6+8×2+2×6)×2
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方厘米)
右面图形体积:
8×6×2-4×3×1
=48×2-12×1
=96-12
=84(立方厘米)
五、作图题(共6分)
23.(6分)长方形纸版上画有15个相同的正方形,用剪刀将它分成三部分,使每一部分都能折成一个无盖的正方体盒子,请在第一部分的每个正方形上标上字母,另外两部分分别标上字母和。
【答案】见详解
【分析】根据正方体展开图的特征,画出三个“1-4-1”型的正方体的展开图,再在每个正方体展开图的一边分别去掉一个小正方形即可。
【解答】
【点评】熟练掌握正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个正方形,第二行放4个正方形,第三行放1个正方形;第二种:“2-2-2”结构,每一行放2个正方形;此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
六、解答题(共38分)
24.(4分)“双减”政策实施后,小轩监督自己的学习情况,每次做完《黄冈名师》里的单元卷都要给自己批改出成绩。在11次的数学测评中平均成绩是91分。在临近期末的最后这次测评成绩出来后,他发现这一次的成绩比这12次测评的平均成绩高5.5分,小轩在第12次测评中得了多少分?
【答案】97分
【分析】可以设小轩在第12次测评中得了x分,11次的数学测评中平均成绩是91分,则11次的数学测评总成绩为(91×11),12次的测评总成绩为(91×11+x),又知第12次测试的成绩比这12次测评的平均成绩高5.5分,则这12次测评的平均成绩为(x-5.5),所以用12次总成绩÷测试的次数=12次测评的平均成绩,据此代入数据,列出方程解答即可。
【解答】解:设小轩第12次测评得了x分。
(91×11+x)÷12=x-5.5
(1001+x)÷12=x-5.5
(1001+x)÷12×12=(x-5.5)×12
1001+x=12x-66
1001+x-x=12x-66-x
1001=11x-66
11x-66+66=1001+66
11x=1067
11x÷11=1067÷11
x=97
答:小轩在第12次测评中得了97分。
25.(4分)政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
【答案】甲工程队15米;乙工程队10米
【分析】设乙工程队平均每天掘进米,则甲工程队平均每天掘进米,根据,,由题意可知等量关系式:甲工程队的工作效率×20+(甲工程队的工作效率+乙工程队的工作效率)×5=425,据此列方程并求解即可得乙工程队的工作效率,用乙工程队的工作效率+5,可得甲工程队的工作效率。
【解答】解:设乙工程队平均每天掘进米,则甲工程队平均每天掘进米。
10+5=15(米)
答:甲工程队平均每天分别掘进15米,乙工程队平均每天分别掘进10米。
26.(4分)甲、乙、丙三位志愿者在一次救灾募捐中积极捐款,乙的捐款数比甲的2倍少100元,丙的捐款数比甲、乙两人的捐款数的和少300元,甲的捐款数是丙的,那么甲捐款多少元?
【答案】800元
【分析】根据题意,设甲捐款元,则乙捐款元,丙捐款元。则根据甲的捐款数是丙的,列出方程解方程即可解答。
【解答】设甲捐款元,则乙捐款元,丙捐款元。
答:甲捐款800元。
【点评】本题考查了列方程解决问题的方法,找到等量关系解方程是解题关键。
27.(4分)小亮做测量“石块体积”的实验,他先将一块棱长是6厘米的正方体铁块浸没在一个长方体水槽中,然后取出正方体铁块,水槽里边的水面下降了2厘米。接着,他把要测量的一个石块浸没在水槽中,这时,水槽里的水面上升了1.5厘米。这个石块的体积是多少立?
【答案】162立方厘米
【分析】由题意可知,下降的水的体积等于棱长是6厘米的正方体铁块的体积,用正方体铁块的体积除以水面下降的高度,求出水槽的底面积,石块的体积等于上升的水的体积,用水槽的底面积乘上升的高度即可求出石块的体积;根据长方体的体积=底面积×高,正方体的体积=棱长×棱长×棱长,据此代入相关数据解答。
【解答】(6×6×6÷2)×1.5
=(36×6÷2)×1.5
=(216÷2)×1.5
=108×1.5
=162(立方厘米)
答:这个石块的体积是162立方厘米。
28.(4分)创卫工作人人有责,爱护环境从我做起。阳光小学组织六年级同学参加创卫活动,共收集了500个易拉罐。六(1)班收集的数量占总数量的,六(1)班男生收集的数量占本班收集数量的,六(1)班女生共收集了多少个易拉罐?
【答案】36个
【分析】先把六年级同学共收集的500个易拉罐看作单位“1”,六(1)班收集的数量占总数量的,单位“1”已知,用六年级收集易拉罐的总数乘,求出六(1)班收集易拉罐的数量;
再把六(1)班收集易拉罐的数量看作单位“1”,六(1)班男生收集的数量占本班收集数量的,则六(1)班女生收集的数量占本班收集数量的(1-),单位“1”已知,用六(1)班收集易拉罐的数量乘(1-),求出六(1)班女生收集易拉罐的数量。
【解答】500××(1-)
=500××
=100×
=36(个)
答:六(一)班女生共收集了36个易拉罐。
29.(4分)如下图,把一个长方体木块正好锯成三个大小相等的小正方体,它们的表面积的和比原来长方体表面积增加了36平方厘米,原来长方体的表面积是多少平方厘米?
【答案】126平方厘米
【分析】根据题意,把一个长方体木块平行于底面锯成三个大小相等的小正方体,说明原长方体的长、宽相等,它们的表面积的和比原来长方体表面积增加了4个底面的面积;
用增加的表面积36平方厘米除以4,求出原长方体的底面积为9平方厘米,因为底面是一个正方形,根据正方形的面积=边长×边长,得出原长方体的长、宽都是3厘米,再乘3,即是原长方体的高;
最后根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出原长方体的表面积。
【解答】36÷4=9(平方厘米)
9=3×3
所以原长方体的长、宽都是3厘米;
原长方体的高:3×3=9(厘米)
原长方体的表面积:
(3×3+3×9+3×9)×2
=(9+27+27)×2
=63×2
=126(平方厘米)
答:原来长方体的表面积是126平方厘米。
30.(4分)有两袋苹果,第一袋质量为千克,如果从第一袋中取出千克放入第二袋中,那么两袋苹果一样重。原来两袋苹果共有多少千克?
【答案】千克
【分析】可设第二袋有x千克苹果,由题意知第一袋中取出千克放入第二袋中,那么两袋苹果一样重,则有,解方程求得第二袋苹果质量,再把两袋质量加起来即可,据此解答。
【解答】解:设第二袋有x千克苹果。
(千克)
答:这两袋共有千克苹果。
31.(10分)下图是某出租车司机2022年下半年收入、支出情况统计图。
月份 7月 8月 9月 10月 11月 12月
收入/万元 0.9 0.2 0.1 0.6 1.3 1.4
支出/万元 0.4 0.3 0.2 0.4 0.6 0.5
(1)根据上面的表格,完成下面的统计图。
(2)该出租车司机2022年下半年( )月份利润最大,是( )万元。(利润=收入-支出)
(3)该出租车司机2022年下半年平均每月的支出是( )万元。
(4)该出租车司机2022年8月份的收入是10月收入的( )。(填最简分数)
【答案】(1)见详解
(2)12,0.9
(3)0.4
(4)
【分析】(1)根据绘制折线统计图的方法,先描点,然后连线,收入用实线连接,支出用虚线;
(2)由于利润=收入减去支出,则找出收入和支出的距离最远,则是利润最大的,也可以用收入的价钱减去支出的价钱,然后比较大小;
(3)根据公式:平均数=总数÷总份数,把下半年支出费用加起来,再除以6即可求解;
(4)用8月份收入除以10月份收入,再根据分数和除法的关系:分子相当于被除数,分母相当于除数,写成分数形式,再根据分数的基本性质把分子和分母约分到公因数只有1的分数。
【解答】(1)
(2)由统计图可知,12月收入和支出距离最远。
1.4-0.5=0.9(万元)
该出租车司机2022年下半年12月份利润最大,是0.9万元。
(3)(0.4+0.3+0.2+0.4+0.6+0.5)÷6
=2.4÷6
=0.4(万元)
该该出租车司机2022年下半年平均每月的支出是0.4万元。
(4)0.2÷0.6=
该出租车司机2022年8月份的收入是10月收入的。
【点评】本题主要考查折线统计图的应用以及平均数的公式、分数和除法的关系,主要是学会分析折线统计图是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版五年级数学下册期末考试综合素养测评检测卷一
一、填空题(共20分)
1.(2分)在讲故事比赛中,7位评委给丽丽的打分数分别是9.9分、10分、8.5分、9.6分、9.5分、9.3分、9.2分,7位评委给丽丽的平均分是( )分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是( )分。(除不尽保留一位小数)
2.(2分)小狗站在百米跑道的终点,看到起点有一个像是它主人的人向它走来。它盯着看了5秒,确定那就是主人,于是它以3米/秒的速度向主人跑去,若主人的行走速度是2米/秒,则小狗跑了( )秒和主人相遇。
3.(2分)如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
4.(2分)下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的( )方向上,孙刘联军在曹军的( )方向上。
5.(2分)鸡的孵化期是21天,鸭的孵化期是鸡的,鸭的孵化期是( )天;鸭的孵化期是鹅的孵化期的,鹅的孵化期是( )天。
6.(2分)一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是( )cm2。体积是( )cm3。
7.(2分)小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了( )页,还剩( )页。
8.(2分)苗圃中的一些苗木很珍贵,园艺工人买了一根20m长的绳子将一些珍贵的苗木保护起来,捆绑沉香苗用去,捆绑一棵紫檀苗用去了m,还剩下绳子( )m。
9.(2分)做一个长8厘米、宽和高都是5厘米的长方体框架,需要( )厘米长的塑料棒,现在外面糊上彩纸,至少需要( )平方厘米的彩纸(接头处忽略不计)。
10.(2分)(小数)。
二、判断题(共10分)
11.(2分)小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。( )
12.(2分)把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
13.(2分)长方形的长是米,宽是米,则它的面积是平方米。( )
14.(2分)3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。( )
15.(2分)动物学校举行了一场运动会,在500米比赛中,小黄狗用了0.62分,小兔子用了分,小黄狗跑得快。( )
三、选择题(共10分)
16.(2分)一列火车长304米,它的速度是每小时126千米,一个骑车人与火车相向而行,全列火车从他身边开过用8秒钟。这个骑车人的速度是每小时( )千米。
A.8 B.10 C.10.2 D.10.8 E.12.6
17.(2分)一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向( )。
A.南偏西30°方向飞行800千米 B.西偏南30°方向飞行800千米
C.北偏东30°方向飞行800千米 D.东偏北30°方向飞行800千米
18.(2分)下列各组数中,互为倒数的是( )。
A.和 B.和 C.和 D.0.5和
19.(2分)在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,( )。
A.增加了 B.减少了 C.不变 D.无法判断
20.(2分)下面四个算式中的“5”和“3”可以直接相加减的是( )。
A.756+342 B.8.54-2.3 C. D.
四、计算题(共16分)
21.(12分)递等式计算。
22.(4分)计算下面图形的表面积和体积。(单位:厘米)
五、作图题(共6分)
23.(6分)长方形纸版上画有15个相同的正方形,用剪刀将它分成三部分,使每一部分都能折成一个无盖的正方体盒子,请在第一部分的每个正方形上标上字母,另外两部分分别标上字母和。
六、解答题(共38分)
24.(4分)“双减”政策实施后,小轩监督自己的学习情况,每次做完《黄冈名师》里的单元卷都要给自己批改出成绩。在11次的数学测评中平均成绩是91分。在临近期末的最后这次测评成绩出来后,他发现这一次的成绩比这12次测评的平均成绩高5.5分,小轩在第12次测评中得了多少分?
25.(4分)政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
26.(4分)甲、乙、丙三位志愿者在一次救灾募捐中积极捐款,乙的捐款数比甲的2倍少100元,丙的捐款数比甲、乙两人的捐款数的和少300元,甲的捐款数是丙的,那么甲捐款多少元?
27.(4分)小亮做测量“石块体积”的实验,他先将一块棱长是6厘米的正方体铁块浸没在一个长方体水槽中,然后取出正方体铁块,水槽里边的水面下降了2厘米。接着,他把要测量的一个石块浸没在水槽中,这时,水槽里的水面上升了1.5厘米。这个石块的体积是多少立?
28.(4分)创卫工作人人有责,爱护环境从我做起。阳光小学组织六年级同学参加创卫活动,共收集了500个易拉罐。六(1)班收集的数量占总数量的,六(1)班男生收集的数量占本班收集数量的,六(1)班女生共收集了多少个易拉罐?
29.(4分)如下图,把一个长方体木块正好锯成三个大小相等的小正方体,它们的表面积的和比原来长方体表面积增加了36平方厘米,原来长方体的表面积是多少平方厘米?
30.(4分)有两袋苹果,第一袋质量为千克,如果从第一袋中取出千克放入第二袋中,那么两袋苹果一样重。原来两袋苹果共有多少千克?
31.(10分)下图是某出租车司机2022年下半年收入、支出情况统计图。
月份 7月 8月 9月 10月 11月 12月
收入/万元 0.9 0.2 0.1 0.6 1.3 1.4
支出/万元 0.4 0.3 0.2 0.4 0.6 0.5
(1)根据上面的表格,完成下面的统计图。
(2)该出租车司机2022年下半年( )月份利润最大,是( )万元。(利润=收入-支出)
(3)该出租车司机2022年下半年平均每月的支出是( )万元。
(4)该出租车司机2022年8月份的收入是10月收入的( )。(填最简分数)
答案解析
一、填空题(共20分)
1.(2分)在讲故事比赛中,7位评委给丽丽的打分数分别是9.9分、10分、8.5分、9.6分、9.5分、9.3分、9.2分,7位评委给丽丽的平均分是( )分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是( )分。(除不尽保留一位小数)
【答案】 9.4 9.5
【分析】根据平均数=总数量÷总份数,求出7位评委给丽丽的平均分;去掉最高分和最低分后,再根据平均数的求法,计算出丽丽的平均得分。保留一位小数看百分位,小于5直接舍去,大于或等于5向前一位进一。
【解答】(9.9+10+8.5+9.6+9.5+9.3+9.2)÷7
=66÷7
≈9.4(分)
(9.9+9.6+9.5+9.3+9.2)÷5
=47.5÷5
=9.5(分)
7位评委给丽丽的平均分是9.4分。如果去掉一个最高分,再去掉一个最低分,丽丽的平均得分是9.5分。
2.(2分)小狗站在百米跑道的终点,看到起点有一个像是它主人的人向它走来。它盯着看了5秒,确定那就是主人,于是它以3米/秒的速度向主人跑去,若主人的行走速度是2米/秒,则小狗跑了( )秒和主人相遇。
【答案】18
【分析】设小狗跑了秒和主人相遇。根据等量关系:100米=小狗秒跑的路程+主人秒行的路程+主人5秒行的路程,列出方程即可求解。
【解答】解:设小狗跑了秒和主人相遇。
3+2+2×5=100
3+2+10=100
5+10=100
5+10-10=100-10
5=90
5÷5=90÷5
=18
小狗跑了18秒和主人相遇。
3.(2分)如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
【答案】 (2a+1) 15
【分析】探究摆a个三角形所需小棒数量规律:
从简单情形入手:摆1个三角形,直接可知需要3根小棒。
分析数量递增关系:摆2个三角形时,第二个三角形与第一个三角形共用1条边,所以相比摆1个三角形,只多了2根小棒,总共用3+2=5根小棒;摆3个三角形时,第三个三角形与前面图形共用1条边,相比摆2个三角形又多了2根小棒,即5+2=7根小棒。依此类推,每增加1个三角形,就增加2根小棒。
推导通用表达式:摆a个三角形,第一个三角形用3根小棒,后面(a-1)个三角形每个都增加2根小棒,所以总共需要小棒数为3+2×(a-1)根。对其化简:
已知摆a个三角形需要2a+1根小棒,现有31根小棒,可据此列出式子2a+1=31,求出三角形的个数。
【解答】摆a个△所需小棒数:
3+2×(a-1)
=3+2a-2
=(2a+1)个
求31根小棒能摆△的个数设31根小棒能摆a个△,则2a+1=31。
2a+1=31
解:2a+1-1=31-1
2a=30a
a=30÷2
a=15
综上,摆a个△需要2a+1根小棒,31根小棒可以摆15个△。
4.(2分)下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的( )方向上,孙刘联军在曹军的( )方向上。
【答案】 西偏北30度 东偏南30度
【分析】根据地图上方向:上北下南左西右东,以孙刘联军为观测点,找到曹军的位置,再根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【解答】下图是小明根据《三国演义》中赤壁之战的情形绘制的曹军与孙刘联军隔江对垒图。曹军在孙刘联军的西偏北30度方向上,孙刘联军在曹军的东偏南30度方向上。
【点评】本题考查根据方向、角度和距离确定物体的位置以及位置的相对性。
5.(2分)鸡的孵化期是21天,鸭的孵化期是鸡的,鸭的孵化期是( )天;鸭的孵化期是鹅的孵化期的,鹅的孵化期是( )天。
【答案】 28 30
【分析】已知鸭的孵化期是鸡的,把鸡的孵化期21天看作单位“1”,单位“1”已知,用鸡的孵化期乘,求出鸭的孵化期;
已知鸭的孵化期是鹅的孵化期的,把鹅的孵化期看作单位“1”,单位“1”未知,用鸭的孵化期除以,求出鹅的孵化期。
【解答】21×=28(天)
28÷
=28×
=30(天)
鸭的孵化期是28天,鹅的孵化期是30天。
6.(2分)一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是( )cm2。体积是( )cm3。
【答案】 504 648
【分析】分析题目,截成的正方体的棱长是6cm,则原来长方体的长是(6×3)cm,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高代入数据列式计算即可。
【解答】6×3=18(cm)
(18×6+18×6+6×6)×2
=(108+108+36)×2
=252×2
=504(cm2)
18×6×6
=108×6
=648(cm3)
一个长方体刚好可以截成三个正方体,这个长方体的宽和高都是6cm,这个长方体的表面积是504cm2。体积是648cm3。
7.(2分)小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了( )页,还剩( )页。
【答案】 35 70
【分析】把这本数的总页数看作单位“1”,第一天看了全书的,求第一天看的页数,用这本数的总页数×解答;求还剩多少页,用这本数的总页数-第一天小明看的页数,即可解答。
【解答】105×=35(页)
105-35=70(页)
小明看一本故事书,共有105页,第一天看了全书的,则第一天小明看了35页,还剩70页。
8.(2分)苗圃中的一些苗木很珍贵,园艺工人买了一根20m长的绳子将一些珍贵的苗木保护起来,捆绑沉香苗用去,捆绑一棵紫檀苗用去了m,还剩下绳子( )m。
【答案】
【分析】由题可知,绳子的总长度是20m,把绳子的总长度看作单位“1”,已知捆绑沉香苗用去,则还剩下(1-),用绳子的总长度乘(1-),求出捆绑沉香苗后剩下的长度,又知捆绑一颗紫檀苗用去了m,再用剩下的绳子长度减去m,即可求出捆绑紫檀苗后剩下的长度。
【解答】20×(1-)-
=20×-
=10-
=(m)
还剩下绳子m。
9.(2分)做一个长8厘米、宽和高都是5厘米的长方体框架,需要( )厘米长的塑料棒,现在外面糊上彩纸,至少需要( )平方厘米的彩纸(接头处忽略不计)。
【答案】 72 210
【分析】求塑料棒的长度就是求棱长总和,因为长方体有4条长,4条宽,4条高;根据“长方体的棱长总和=(长+宽+高)×4”进行解答即可;求需要彩纸的面积,就是求长方体的表面积,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”"进行解答即可。
【解答】(8+5+5)×4
=18×4
=72(厘米)
(8×5+8×5+5×5)×2
=(40+40+25)×2
=105×2
=210(平方厘米)
所以做一个长8厘米、宽和高都是5厘米的长方体框架,需要72厘米长的塑料棒,现在外面糊上彩纸,至少需要210平方厘米的彩纸。
10.(2分)(小数)。
【答案】9;20;40;0.6
【分析】根据分数的基本性质,的分子和分母都乘8就是,的分子和分母都乘3就是;根据分数与除法的关系,=3÷5,根据商不变的规律,3÷5=12÷20;把化成小数是0.6;据此解答。
【解答】=12÷20===0.6
二、判断题(共10分)
11.(2分)小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。( )
【答案】√
【分析】由位置的相对性可知,当观测点相反时,观察到的方向就正好相反,角度不变,南偏东的相反方向是北偏西,据此判断。
【解答】小猴子住在小松鼠家南偏东30°方向上,那么小松鼠家在小猴子家北偏西30°方向上。说法正确。
故答案为:√
12.(2分)把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
【答案】√
【分析】把一个长方体切成两个相同的小长方体,因为面数目增加,所以表面积增加,但是体积没变,据此分析。
【解答】
如图,把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变,说法正确。
故答案为:√
13.(2分)长方形的长是米,宽是米,则它的面积是平方米。( )
【答案】√
【分析】长方形面积=长×宽,由此计算出这个长方形的面积即可。
【解答】×=(平方米)
所以,长方形的面积是平方米。
故答案为:√
14.(2分)3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。( )
【答案】√
【分析】从正面看有3个面露在外面,从上面看有2个面露在外面,从右边看有2个面露在外面,一共有3+2+2个面露在外面,再根据正方形面积公式:面积=边长×边长,求出一个正方体的面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,再进行比较,即可解答。
【解答】2×2×(3+2+2)
=4×(5+2)
=4×7
=28(cm2)
3个棱长为2cm的正方体放在墙角(如图),露在外面的面积是。
原题干说法正确。
故答案为:√
【点评】解答本题的关键是求出露在外面的个数。
15.(2分)动物学校举行了一场运动会,在500米比赛中,小黄狗用了0.62分,小兔子用了分,小黄狗跑得快。( )
【答案】√
【分析】同样的距离,时间越少速度越快,据此比较小黄狗和小兔子用的时间即可。小数与分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【解答】=16÷25=0.64
0.62<,小黄狗跑得快,说法正确。
故答案为:√
三、选择题(共10分)
16.(2分)一列火车长304米,它的速度是每小时126千米,一个骑车人与火车相向而行,全列火车从他身边开过用8秒钟。这个骑车人的速度是每小时( )千米。
A.8 B.10 C.10.2 D.10.8 E.12.6
【答案】D
【分析】根据速度和=总路程÷时间,先用304除以8求出两者的速度和,然后转化单位,再减去火车的速度即可。
【解答】304÷8=38(米/秒)
38米/秒=136.8千米/小时
136.8﹣126=10.8(千米/小时)
所以这个骑车人的速度是每小时10.8千米。
故答案选:D
17.(2分)一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向( )。
A.南偏西30°方向飞行800千米 B.西偏南30°方向飞行800千米
C.北偏东30°方向飞行800千米 D.东偏北30°方向飞行800千米
【答案】D
【分析】一架飞机从某机场向南偏西60°方向飞行了800千米,原路返回时飞机飞行的距离不变,与来时的方向完全相反,偏的角度不变。据此解答即可。
【解答】一架飞机从某机场向南偏西60°方向飞行了800千米,沿原路返回时飞机要向北偏东60°方向或东偏北30°方向,飞行800千米。
故答案为:D
【点评】方向是相对的,以点A的位置为观测点看点B与以点B的位置为观测点点A,方向完全相反,所偏的度数及距离不变。
18.(2分)下列各组数中,互为倒数的是( )。
A.和 B.和 C.和 D.0.5和
【答案】B
【分析】乘积是1的两个数互为倒数。据此分别计算各选项中两个数的乘积即可解答。
【解答】A.×=,则和不互为倒数;
B.×=1,则和互为倒数;
C.×=,则和不互为倒数;
D.0.5×=,则0.5和不互为倒数。
故答案为:B
19.(2分)在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,( )。
A.增加了 B.减少了 C.不变 D.无法判断
【答案】C
【分析】原来大正方体的表面积需要计算小长方体上面、正面、右面的面积,挖掉小长方体后剩下物体的表面积需要计算小长方体下面、后面、左面的面积,其余部分面积不变,小长方体相对的面完全相同,则表面积不变;据此选择。
【解答】由分析可得:在一个棱长是10cm的正方体的一角,切去一个小长方体(如下图),它的表面积和原正方体的表面积相比,不变。
故答案为:C
20.(2分)下面四个算式中的“5”和“3”可以直接相加减的是( )。
A.756+342 B.8.54-2.3 C. D.
【答案】B
【分析】计算整数和小数的加减法,相同数位要对齐,即计数单位相同的数才能相加减。异分母分数相加减,先通分,化成同分母分数,再相加减,即分数单位相同的分数,才能把分子相加减。
【解答】A.756中5在十位上,表示5个十,342中3在百位上,表示3个百,计数单位不同,不能直接相加。
B.8.54中5在十分位上,表示5个0.1,2.3中3在十分位上,表示3个0.1,计数单位相同,能直接相加。
C.的分数单位是,表示5个,的分数单位是,表示3个,分数单位不同,不能直接相减
D.5表示5个一,的分数单位是,表示3个,计数单位不同,不能直接相加。
故答案为:B
四、计算题(共16分)
21.(12分)递等式计算。
【答案】;;5
;;23.4
【分析】(1)运用加法的结合律进行简算;
(2)运用减法的性质、加法的交换律进行简算;
(3)先算除法,再算减法;
(4)直接约分进行计算;
(5)运用减法的性质进行简算;
(6)先算乘法,再算加法。
【解答】(1)
=
=
=
(2)
=
=
=1-
=
(3)
=6-
=5
(4)
=
=
=
(5)
=
=
=
(6)
=9+14.4
=23.4
22.(4分)计算下面图形的表面积和体积。(单位:厘米)
【答案】左图:190平方厘米;105立方厘米
右图:152平方厘米;84立方厘米
【分析】左图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为10厘米,宽5厘米,高3厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立体图形的体积,可以看作两个长方体的体积,一个是下面的扁一点的长方体,该长方体长为10厘米,宽为5厘米,高为1.5厘米,另外一个长方体是在上方的稍微小一点的长方体,该长方体长为10厘米,宽为2厘米,高为(3-1.5)厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
右图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为8厘米,宽6厘米,高2厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立方体的体积,可以看作大的长方体的体积减去一个小长方体体积,小长方体长为4厘米,宽为3厘米,高为1厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
【解答】由分析可得:
左面图形表面积:
(10×5+10×3+3×5)×2
=(50+30+15)×2
=(80+15)×2
=95×2
=190(平方厘米)
左面图形体积:
10×5×1.5+10×2×(3-1.5)
=50×1.5+10×2×1.5
=75+20×1.5
=75+30
=105(立方厘米)
右面图形表面积:
(8×6+8×2+2×6)×2
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方厘米)
右面图形体积:
8×6×2-4×3×1
=48×2-12×1
=96-12
=84(立方厘米)
五、作图题(共6分)
23.(6分)长方形纸版上画有15个相同的正方形,用剪刀将它分成三部分,使每一部分都能折成一个无盖的正方体盒子,请在第一部分的每个正方形上标上字母,另外两部分分别标上字母和。
【答案】见详解
【分析】根据正方体展开图的特征,画出三个“1-4-1”型的正方体的展开图,再在每个正方体展开图的一边分别去掉一个小正方形即可。
【解答】
【点评】熟练掌握正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个正方形,第二行放4个正方形,第三行放1个正方形;第二种:“2-2-2”结构,每一行放2个正方形;此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
六、解答题(共38分)
24.(4分)“双减”政策实施后,小轩监督自己的学习情况,每次做完《黄冈名师》里的单元卷都要给自己批改出成绩。在11次的数学测评中平均成绩是91分。在临近期末的最后这次测评成绩出来后,他发现这一次的成绩比这12次测评的平均成绩高5.5分,小轩在第12次测评中得了多少分?
【答案】97分
【分析】可以设小轩在第12次测评中得了x分,11次的数学测评中平均成绩是91分,则11次的数学测评总成绩为(91×11),12次的测评总成绩为(91×11+x),又知第12次测试的成绩比这12次测评的平均成绩高5.5分,则这12次测评的平均成绩为(x-5.5),所以用12次总成绩÷测试的次数=12次测评的平均成绩,据此代入数据,列出方程解答即可。
【解答】解:设小轩第12次测评得了x分。
(91×11+x)÷12=x-5.5
(1001+x)÷12=x-5.5
(1001+x)÷12×12=(x-5.5)×12
1001+x=12x-66
1001+x-x=12x-66-x
1001=11x-66
11x-66+66=1001+66
11x=1067
11x÷11=1067÷11
x=97
答:小轩在第12次测评中得了97分。
25.(4分)政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
【答案】甲工程队15米;乙工程队10米
【分析】设乙工程队平均每天掘进米,则甲工程队平均每天掘进米,根据,,由题意可知等量关系式:甲工程队的工作效率×20+(甲工程队的工作效率+乙工程队的工作效率)×5=425,据此列方程并求解即可得乙工程队的工作效率,用乙工程队的工作效率+5,可得甲工程队的工作效率。
【解答】解:设乙工程队平均每天掘进米,则甲工程队平均每天掘进米。
10+5=15(米)
答:甲工程队平均每天分别掘进15米,乙工程队平均每天分别掘进10米。
26.(4分)甲、乙、丙三位志愿者在一次救灾募捐中积极捐款,乙的捐款数比甲的2倍少100元,丙的捐款数比甲、乙两人的捐款数的和少300元,甲的捐款数是丙的,那么甲捐款多少元?
【答案】800元
【分析】根据题意,设甲捐款元,则乙捐款元,丙捐款元。则根据甲的捐款数是丙的,列出方程解方程即可解答。
【解答】设甲捐款元,则乙捐款元,丙捐款元。
答:甲捐款800元。
【点评】本题考查了列方程解决问题的方法,找到等量关系解方程是解题关键。
27.(4分)小亮做测量“石块体积”的实验,他先将一块棱长是6厘米的正方体铁块浸没在一个长方体水槽中,然后取出正方体铁块,水槽里边的水面下降了2厘米。接着,他把要测量的一个石块浸没在水槽中,这时,水槽里的水面上升了1.5厘米。这个石块的体积是多少立?
【答案】162立方厘米
【分析】由题意可知,下降的水的体积等于棱长是6厘米的正方体铁块的体积,用正方体铁块的体积除以水面下降的高度,求出水槽的底面积,石块的体积等于上升的水的体积,用水槽的底面积乘上升的高度即可求出石块的体积;根据长方体的体积=底面积×高,正方体的体积=棱长×棱长×棱长,据此代入相关数据解答。
【解答】(6×6×6÷2)×1.5
=(36×6÷2)×1.5
=(216÷2)×1.5
=108×1.5
=162(立方厘米)
答:这个石块的体积是162立方厘米。
28.(4分)创卫工作人人有责,爱护环境从我做起。阳光小学组织六年级同学参加创卫活动,共收集了500个易拉罐。六(1)班收集的数量占总数量的,六(1)班男生收集的数量占本班收集数量的,六(1)班女生共收集了多少个易拉罐?
【答案】36个
【分析】先把六年级同学共收集的500个易拉罐看作单位“1”,六(1)班收集的数量占总数量的,单位“1”已知,用六年级收集易拉罐的总数乘,求出六(1)班收集易拉罐的数量;
再把六(1)班收集易拉罐的数量看作单位“1”,六(1)班男生收集的数量占本班收集数量的,则六(1)班女生收集的数量占本班收集数量的(1-),单位“1”已知,用六(1)班收集易拉罐的数量乘(1-),求出六(1)班女生收集易拉罐的数量。
【解答】500××(1-)
=500××
=100×
=36(个)
答:六(一)班女生共收集了36个易拉罐。
29.(4分)如下图,把一个长方体木块正好锯成三个大小相等的小正方体,它们的表面积的和比原来长方体表面积增加了36平方厘米,原来长方体的表面积是多少平方厘米?
【答案】126平方厘米
【分析】根据题意,把一个长方体木块平行于底面锯成三个大小相等的小正方体,说明原长方体的长、宽相等,它们的表面积的和比原来长方体表面积增加了4个底面的面积;
用增加的表面积36平方厘米除以4,求出原长方体的底面积为9平方厘米,因为底面是一个正方形,根据正方形的面积=边长×边长,得出原长方体的长、宽都是3厘米,再乘3,即是原长方体的高;
最后根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出原长方体的表面积。
【解答】36÷4=9(平方厘米)
9=3×3
所以原长方体的长、宽都是3厘米;
原长方体的高:3×3=9(厘米)
原长方体的表面积:
(3×3+3×9+3×9)×2
=(9+27+27)×2
=63×2
=126(平方厘米)
答:原来长方体的表面积是126平方厘米。
30.(4分)有两袋苹果,第一袋质量为千克,如果从第一袋中取出千克放入第二袋中,那么两袋苹果一样重。原来两袋苹果共有多少千克?
【答案】千克
【分析】可设第二袋有x千克苹果,由题意知第一袋中取出千克放入第二袋中,那么两袋苹果一样重,则有,解方程求得第二袋苹果质量,再把两袋质量加起来即可,据此解答。
【解答】解:设第二袋有x千克苹果。
(千克)
答:这两袋共有千克苹果。
31.(10分)下图是某出租车司机2022年下半年收入、支出情况统计图。
月份 7月 8月 9月 10月 11月 12月
收入/万元 0.9 0.2 0.1 0.6 1.3 1.4
支出/万元 0.4 0.3 0.2 0.4 0.6 0.5
(1)根据上面的表格,完成下面的统计图。
(2)该出租车司机2022年下半年( )月份利润最大,是( )万元。(利润=收入-支出)
(3)该出租车司机2022年下半年平均每月的支出是( )万元。
(4)该出租车司机2022年8月份的收入是10月收入的( )。(填最简分数)
【答案】(1)见详解
(2)12,0.9
(3)0.4
(4)
【分析】(1)根据绘制折线统计图的方法,先描点,然后连线,收入用实线连接,支出用虚线;
(2)由于利润=收入减去支出,则找出收入和支出的距离最远,则是利润最大的,也可以用收入的价钱减去支出的价钱,然后比较大小;
(3)根据公式:平均数=总数÷总份数,把下半年支出费用加起来,再除以6即可求解;
(4)用8月份收入除以10月份收入,再根据分数和除法的关系:分子相当于被除数,分母相当于除数,写成分数形式,再根据分数的基本性质把分子和分母约分到公因数只有1的分数。
【解答】(1)
(2)由统计图可知,12月收入和支出距离最远。
1.4-0.5=0.9(万元)
该出租车司机2022年下半年12月份利润最大,是0.9万元。
(3)(0.4+0.3+0.2+0.4+0.6+0.5)÷6
=2.4÷6
=0.4(万元)
该该出租车司机2022年下半年平均每月的支出是0.4万元。
(4)0.2÷0.6=
该出租车司机2022年8月份的收入是10月收入的。
【点评】本题主要考查折线统计图的应用以及平均数的公式、分数和除法的关系,主要是学会分析折线统计图是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
