第2章 函数 3 第1课时 函数的单调性--北师大版高中数学必修第一册课件(共42页PPT)
文档属性
| 名称 | 第2章 函数 3 第1课时 函数的单调性--北师大版高中数学必修第一册课件(共42页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:31:40 | ||
图片预览









文档简介
(共42张PPT)
第二章
§3 第1课时 函数的单调性
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解函数单调性的概念.
2.会根据函数的图象判断函数的单调性.
3.能够根据函数单调性的定义证明函数在某一区间上的单调性.
基础落实·必备知识一遍过
知识点1 单调性、单调区间
单调性 单调递增 单调递减
条件 设函数y=f(x)的定义域是D,I是定义域D上的一个区间,如果对于任意的x1,x2∈I,当x1f(x2)
结论 称函数y=f(x)在区间I上单调递增 称函数y=f(x)在区间I上单调递减
单调 区间 区间I叫作函数y=f(x)的单调递增区间 区间I叫作函数y=f(x)的单调递减区间
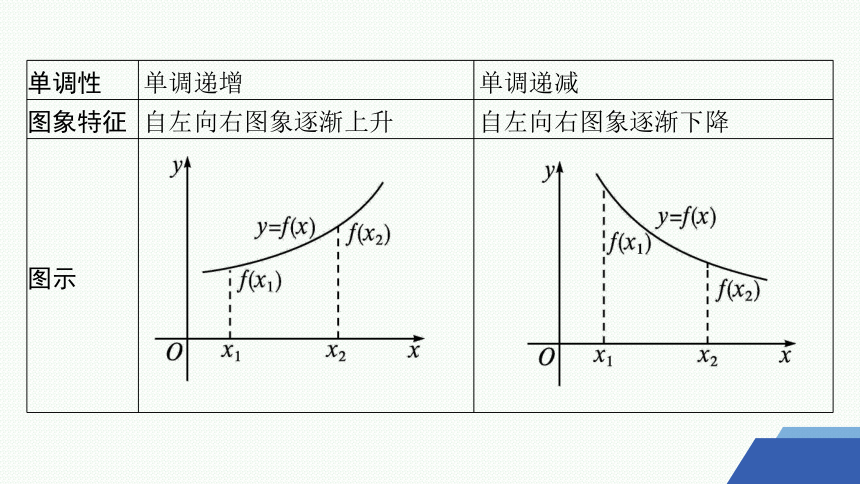
单调性 单调递增 单调递减
图象特征 自左向右图象逐渐上升 自左向右图象逐渐下降
图示
如果函数y=f(x)在区间I上单调递增或单调递减,那么就称函数y=f(x)在区间I上具有单调性.单调递增区间和单调递减区间统称为单调区间.
单调性是函数的局部性质
名师点睛
x1,x2的三个特征:
(1)同区间性,即x1,x2∈D;
(2)任意性,即不可用区间D上的两个特殊值代替x1,x2;
(3)有序性,即需要区分大小,通常规定x1思考辨析
在函数单调性的定义中,能否去掉“任意”
提示 不能,不能用特殊代替一般.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)函数单调性定义中的“任意两个自变量的值x1,x2”可以改为“存在两个自变量的值x1,x2”.( )
(2)若函数y=f(x)在I上满足f(1)(3)函数f(x)= 在定义域上单调递减.( )
×
×
×
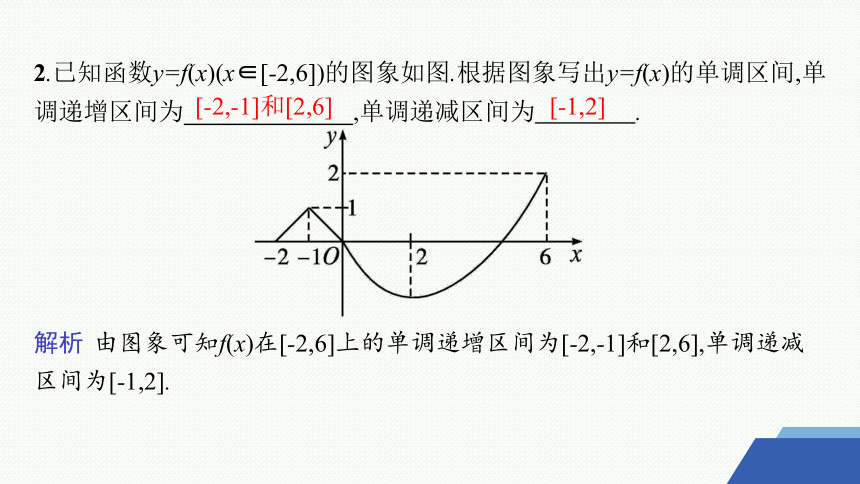
2.已知函数y=f(x)(x∈[-2,6])的图象如图.根据图象写出y=f(x)的单调区间,单调递增区间为 ,单调递减区间为 .
[-2,-1]和[2,6]
[-1,2]
解析 由图象可知f(x)在[-2,6]上的单调递增区间为[-2,-1]和[2,6],单调递减区间为[-1,2].
3.[人教A版教材习题]画出下列函数的图象,并根据图象说出函数y=f(x)的单调区间及在每一单调区间上的单调性.
(1)y=x2-5x-6;(2)y=9-x2.
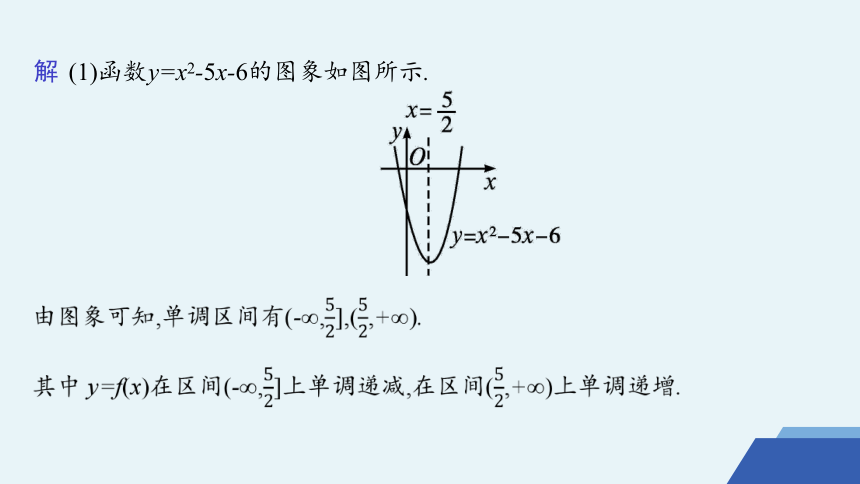
解 (1)函数y=x2-5x-6的图象如图所示.
(2)函数y=9-x2的图象如图所示.
由图象可知,单调区间有(-∞,0],[0,+∞).
其中y=f(x)在区间(-∞,0]上单调递增,在区间[0,+∞)上单调递减.
知识点2 增函数、减函数的定义
函数 增函数 减函数
条件 设函数y=f(x)的定义域是D,如果对于任意的x1,x2∈D,当x1f(x2)
结论 称函数y=f(x)是增函数 称函数y=f(x)是减函数
名师点睛
1.若f(x),g(x)均是区间A上的增(减)函数,则f(x)+g(x)也是区间A上的增(减)函数;若f(x),g(x)分别是区间A上的增函数和减函数,则f(x)-g(x)是区间A上的增函数.
2.若k>0,则kf(x)与f(x)的单调性相同;若k<0,则kf(x)与f(x)的单调性相反.
思考辨析
若函数f(x)在区间(1,2]和(2,3)上均单调递增,你能得出函数f(x)在区间(1,3)上单调递增吗
提示 不能得出.函数图象是连续的才可以得出,有的分段函数不能得出.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)一个函数f(x)不是增函数,就是减函数.( )
(2)若函数f(x)为R上的减函数,则f(-3)>f(3).( )
(3)若函数f(x)为定义在R上的函数且满足f(-3)>f(3),则函数f(x)为R上的减函数.( )
×
√
×
2.[人教B版教材例题]求证:函数f(x)=-2x在R上是减函数.
证明 任取x1,x2∈R且x10,从而f(x1)>f(x2).因此,函数f(x)=-2x在R上是减函数.
重难探究·能力素养速提升
探究点一 判断函数的单调性
角度1利用图象判断函数的单调性
【例1-1】 根据函数图象直观判断下列函数的单调性:
(1)y=|x2+2x-3|;(2)y=-x2+2|x|+1.
解 (1)令f(x)=x2+2x-3=(x+1)2-4.作出f(x)的图象,保留其在x轴上及x轴上方部分,将位于x轴下方的部分翻折到x轴上方,得到y=|x2+2x-3|的图象,如图所示.
由图象可得原函数在区间[-3,-1]和[1,+∞)上单调递增,原函数在区间(-∞,-3]和[-1,1]上单调递减.
函数图象如图所示,原函数在区间(-∞,-1]和[0,1]上单调递增,在区间[-1,0]和[1,+∞)上单调递减.
规律方法 图象法判断函数单调性的注意点
图象法判断函数的单调性主要用于常见函数(如一次函数、二次函数、反比例函数等)的单调性判断,或应用于能通过常见函数图象的平移、翻折等变换得到所给函数的图象,从而进行单调性的判断.
变式训练1已知x∈R,函数f(x)=x|x-2|,试画出y=f(x)的图象,并结合图象判断函数的单调性.
图象如图所示.
由图象可知,函数在区间(-∞,1],[2,+∞)上单调递增;在区间[1,2]上单调递减.
角度2利用单调函数的运算性质判断函数的单调性
【例1-2】 判断函数 的单调性.
规律方法 利用单调函数的运算性质判断函数单调性的思路
当函数解析式通过变换、转化之后,是由几个基本函数的解析式构成的,则可分析这几个基本函数的单调性,则看是否符合单调函数运算性质的规律,若符合,可直接得出结论,否则,不能用这种方法判断函数的单调性.此外,研究函数的单调性时,一定要坚持“定义域优先”的原则.
变式训练2判断函数 (x<0)的单调性.
探究点二 利用定义证明或判断函数的单调性
【例2】 证明:函数f(x)=-2x2+3x+3在区间(-∞, ]上单调递增.
规律方法 利用定义证明或判断函数的单调性的步骤
探究点三 函数单调性的应用
【例3】 (1)若函数 在R上单调递增,则实数a的取值范围是 .
(0,3]
★(2)已知函数f(x)在区间(0,+∞)上单调递减,试比较f(a2-a+1)与 的大小.
规律方法 1.利用函数的单调性可以比较函数值或自变量的大小.在利用函数的单调性比较函数值大小时,要注意将对应的自变量转化到同一个单调区间内.
2.利用函数的单调性解有关函数值的不等式就是利用函数在某个区间内的单调性,去掉对应关系“f”,转化为自变量的不等式,此时一定要注意自变量的限制条件,以防出错.
3.由分段函数单调性求参数取值范围时,一般从两个方面思考:一方面每个分段区间上函数具有相同的单调性,由此列出相关式子;另一方面是考虑端点处的衔接情况,由此列出另一相关式子,求解即可.
变式训练4(1)[2024湖北武汉高一期末]已知f(2x)=|x-a|,若函数f(x)在区间
(-∞,2]上单调递减,则实数a的取值范围是( )
A.[1,+∞) B.(1,+∞)
C.[2,+∞) D.(2,+∞)
A
★(2)已知函数g(x)的定义域是[-2,2],且在定义域[-2,2]上单调递增,g(t)>g(1-3t),求t的取值范围.
本节要点归纳
1.知识清单:
(1)增函数、减函数的定义;
(2)函数单调性的定义及单调区间的确定.
2.方法归纳:数形结合法、定义法.
3.常见误区:函数具有多个单调区间时,单调区间之间用“,”与“和”连接,含参数的分段函数的单调性易忽视定义域端点处函数值的大小.
学以致用·随堂检测促达标
1
2
3
4
5
1.函数y=f(x)的图象如图所示,其单调递减区间是( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-4,-3],[1,4]
D.[-3,1]
C
1
2
3
4
5
2.下列函数不在区间(0,+∞)上单调递增的是( )
A.y=2x+1 B.y=3x2+1
C.y= D.y=|x|
C
1
2
3
4
5
3.[2024广东惠州高一月考]已知函数f(x)=ax+1在R上单调递减,则函数g(x)=a(x2-4x+3)的单调递增区间为( )
A.(-2,+∞) B.(2,+∞)
C.(-∞,2) D.(-∞,-2)
C
解析 ∵函数f(x)=ax+1在R上单调递减,∴a<0,∴g(x)=a(x2-4x+3)的图象为开口向下的抛物线,其对称轴方程为x=2,∴g(x)在(-∞,2)上单调递增,即函数g(x)=a(x2-4x+3)的单调递增区间为(-∞,2).故选C.
1
2
3
4
5
4.已知函数f(x)为定义在区间[-1,1]上的增函数,则满足f(x)1
2
3
4
5
5.求证:函数 在区间(0,+∞)上单调递减.
证明 任取x1,x2∈(0,+∞),且x1∵00,x2+x1>0, >0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴函数f(x)= 在区间(0,+∞)上单调递减.
本 课 结 束
第二章
§3 第1课时 函数的单调性
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解函数单调性的概念.
2.会根据函数的图象判断函数的单调性.
3.能够根据函数单调性的定义证明函数在某一区间上的单调性.
基础落实·必备知识一遍过
知识点1 单调性、单调区间
单调性 单调递增 单调递减
条件 设函数y=f(x)的定义域是D,I是定义域D上的一个区间,如果对于任意的x1,x2∈I,当x1
结论 称函数y=f(x)在区间I上单调递增 称函数y=f(x)在区间I上单调递减
单调 区间 区间I叫作函数y=f(x)的单调递增区间 区间I叫作函数y=f(x)的单调递减区间
单调性 单调递增 单调递减
图象特征 自左向右图象逐渐上升 自左向右图象逐渐下降
图示
如果函数y=f(x)在区间I上单调递增或单调递减,那么就称函数y=f(x)在区间I上具有单调性.单调递增区间和单调递减区间统称为单调区间.
单调性是函数的局部性质
名师点睛
x1,x2的三个特征:
(1)同区间性,即x1,x2∈D;
(2)任意性,即不可用区间D上的两个特殊值代替x1,x2;
(3)有序性,即需要区分大小,通常规定x1
在函数单调性的定义中,能否去掉“任意”
提示 不能,不能用特殊代替一般.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)函数单调性定义中的“任意两个自变量的值x1,x2”可以改为“存在两个自变量的值x1,x2”.( )
(2)若函数y=f(x)在I上满足f(1)
×
×
×
2.已知函数y=f(x)(x∈[-2,6])的图象如图.根据图象写出y=f(x)的单调区间,单调递增区间为 ,单调递减区间为 .
[-2,-1]和[2,6]
[-1,2]
解析 由图象可知f(x)在[-2,6]上的单调递增区间为[-2,-1]和[2,6],单调递减区间为[-1,2].
3.[人教A版教材习题]画出下列函数的图象,并根据图象说出函数y=f(x)的单调区间及在每一单调区间上的单调性.
(1)y=x2-5x-6;(2)y=9-x2.
解 (1)函数y=x2-5x-6的图象如图所示.
(2)函数y=9-x2的图象如图所示.
由图象可知,单调区间有(-∞,0],[0,+∞).
其中y=f(x)在区间(-∞,0]上单调递增,在区间[0,+∞)上单调递减.
知识点2 增函数、减函数的定义
函数 增函数 减函数
条件 设函数y=f(x)的定义域是D,如果对于任意的x1,x2∈D,当x1
结论 称函数y=f(x)是增函数 称函数y=f(x)是减函数
名师点睛
1.若f(x),g(x)均是区间A上的增(减)函数,则f(x)+g(x)也是区间A上的增(减)函数;若f(x),g(x)分别是区间A上的增函数和减函数,则f(x)-g(x)是区间A上的增函数.
2.若k>0,则kf(x)与f(x)的单调性相同;若k<0,则kf(x)与f(x)的单调性相反.
思考辨析
若函数f(x)在区间(1,2]和(2,3)上均单调递增,你能得出函数f(x)在区间(1,3)上单调递增吗
提示 不能得出.函数图象是连续的才可以得出,有的分段函数不能得出.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)一个函数f(x)不是增函数,就是减函数.( )
(2)若函数f(x)为R上的减函数,则f(-3)>f(3).( )
(3)若函数f(x)为定义在R上的函数且满足f(-3)>f(3),则函数f(x)为R上的减函数.( )
×
√
×
2.[人教B版教材例题]求证:函数f(x)=-2x在R上是减函数.
证明 任取x1,x2∈R且x1
重难探究·能力素养速提升
探究点一 判断函数的单调性
角度1利用图象判断函数的单调性
【例1-1】 根据函数图象直观判断下列函数的单调性:
(1)y=|x2+2x-3|;(2)y=-x2+2|x|+1.
解 (1)令f(x)=x2+2x-3=(x+1)2-4.作出f(x)的图象,保留其在x轴上及x轴上方部分,将位于x轴下方的部分翻折到x轴上方,得到y=|x2+2x-3|的图象,如图所示.
由图象可得原函数在区间[-3,-1]和[1,+∞)上单调递增,原函数在区间(-∞,-3]和[-1,1]上单调递减.
函数图象如图所示,原函数在区间(-∞,-1]和[0,1]上单调递增,在区间[-1,0]和[1,+∞)上单调递减.
规律方法 图象法判断函数单调性的注意点
图象法判断函数的单调性主要用于常见函数(如一次函数、二次函数、反比例函数等)的单调性判断,或应用于能通过常见函数图象的平移、翻折等变换得到所给函数的图象,从而进行单调性的判断.
变式训练1已知x∈R,函数f(x)=x|x-2|,试画出y=f(x)的图象,并结合图象判断函数的单调性.
图象如图所示.
由图象可知,函数在区间(-∞,1],[2,+∞)上单调递增;在区间[1,2]上单调递减.
角度2利用单调函数的运算性质判断函数的单调性
【例1-2】 判断函数 的单调性.
规律方法 利用单调函数的运算性质判断函数单调性的思路
当函数解析式通过变换、转化之后,是由几个基本函数的解析式构成的,则可分析这几个基本函数的单调性,则看是否符合单调函数运算性质的规律,若符合,可直接得出结论,否则,不能用这种方法判断函数的单调性.此外,研究函数的单调性时,一定要坚持“定义域优先”的原则.
变式训练2判断函数 (x<0)的单调性.
探究点二 利用定义证明或判断函数的单调性
【例2】 证明:函数f(x)=-2x2+3x+3在区间(-∞, ]上单调递增.
规律方法 利用定义证明或判断函数的单调性的步骤
探究点三 函数单调性的应用
【例3】 (1)若函数 在R上单调递增,则实数a的取值范围是 .
(0,3]
★(2)已知函数f(x)在区间(0,+∞)上单调递减,试比较f(a2-a+1)与 的大小.
规律方法 1.利用函数的单调性可以比较函数值或自变量的大小.在利用函数的单调性比较函数值大小时,要注意将对应的自变量转化到同一个单调区间内.
2.利用函数的单调性解有关函数值的不等式就是利用函数在某个区间内的单调性,去掉对应关系“f”,转化为自变量的不等式,此时一定要注意自变量的限制条件,以防出错.
3.由分段函数单调性求参数取值范围时,一般从两个方面思考:一方面每个分段区间上函数具有相同的单调性,由此列出相关式子;另一方面是考虑端点处的衔接情况,由此列出另一相关式子,求解即可.
变式训练4(1)[2024湖北武汉高一期末]已知f(2x)=|x-a|,若函数f(x)在区间
(-∞,2]上单调递减,则实数a的取值范围是( )
A.[1,+∞) B.(1,+∞)
C.[2,+∞) D.(2,+∞)
A
★(2)已知函数g(x)的定义域是[-2,2],且在定义域[-2,2]上单调递增,g(t)>g(1-3t),求t的取值范围.
本节要点归纳
1.知识清单:
(1)增函数、减函数的定义;
(2)函数单调性的定义及单调区间的确定.
2.方法归纳:数形结合法、定义法.
3.常见误区:函数具有多个单调区间时,单调区间之间用“,”与“和”连接,含参数的分段函数的单调性易忽视定义域端点处函数值的大小.
学以致用·随堂检测促达标
1
2
3
4
5
1.函数y=f(x)的图象如图所示,其单调递减区间是( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-4,-3],[1,4]
D.[-3,1]
C
1
2
3
4
5
2.下列函数不在区间(0,+∞)上单调递增的是( )
A.y=2x+1 B.y=3x2+1
C.y= D.y=|x|
C
1
2
3
4
5
3.[2024广东惠州高一月考]已知函数f(x)=ax+1在R上单调递减,则函数g(x)=a(x2-4x+3)的单调递增区间为( )
A.(-2,+∞) B.(2,+∞)
C.(-∞,2) D.(-∞,-2)
C
解析 ∵函数f(x)=ax+1在R上单调递减,∴a<0,∴g(x)=a(x2-4x+3)的图象为开口向下的抛物线,其对称轴方程为x=2,∴g(x)在(-∞,2)上单调递增,即函数g(x)=a(x2-4x+3)的单调递增区间为(-∞,2).故选C.
1
2
3
4
5
4.已知函数f(x)为定义在区间[-1,1]上的增函数,则满足f(x)
2
3
4
5
5.求证:函数 在区间(0,+∞)上单调递减.
证明 任取x1,x2∈(0,+∞),且x1
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴函数f(x)= 在区间(0,+∞)上单调递减.
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
