北师大版2019必修第一册2.2.2 函数的表示法 课件(共16张PPT)
文档属性
| 名称 | 北师大版2019必修第一册2.2.2 函数的表示法 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:00:52 | ||
图片预览




文档简介
(共16张PPT)
2.2函数的表示法
北师大版(2019)高中数学必修第一册
第二章 函数
第2节 函数
导入课题
新知讲授
典例剖析
课堂小结
初中我们学习了三种重要的函数类型,
一次函数
二次函数
反比例函数
三个函数都是用解析法表示的函数,在初中,我们就学习了三种函数的
表示方法:解析法、列表法、图像法,不同的问题适用不同的表示方法,因此,
今天我们要更加深入地学习函数的表示法.
一、函数的表示法
导入课题
解析法:用一个等式来表示变量之间的函数对应关系的方法叫作解析法.
这个等式叫做函数的解析式.
优点:变量之间的关系明确,便于精确计算,
例如,初中学习的一次函数,一元二次函数,反比例函数等都是用解析法表示的.
缺点:不够直观,某些函数无法用解析式表示.
例如,下图(心电图)
强度是时间的函数,但是我们没法用精确的解析式把函数表示出来.
列表法:用表格给出变量之间的函数对应关系的方法叫作列表法.
优点:列表法直接通过表格读数,不必通过计算,就表示出了两个变量之间的对应值,非常直观.
缺点:任何一个表格内标出的数都是有限个,也就只能表示有限个数值之间的函数关系.
新知探究
典例剖析
课堂小结
一、函数的表示法
导入课题
图象法:用图形给出变量之间的函数对应关系的方法叫作图象法.
优点:能直观地显示出变量的关系、变化规律和函数的性质,弥补了数、式的枯燥与抽象,是“数形
结合”思想方法的主要内容之一,不仅在研究函数中经常使用,在日常生活中用途也非常广泛.
缺点:无法进行精确运算,并非所有的函数都能用图像法表示.
例如,只有函数图象时,很多时候无法求出函数定义域、求精确的函数值等.
例如,狄利克雷函数,无法用图像法表示.
为了清楚地表示一个函数关系,需要有针对性地选择适当的表示方法,有时需要多种方法综合运用.
在实际问题中,还常常需要把函数的某种表示方法转化为另一种表示方法,这样才可以更清楚、全
面的了解函数的性质.
新知探究
典例剖析
课堂小结
导入课题
新知探究
典例剖析
课堂小结
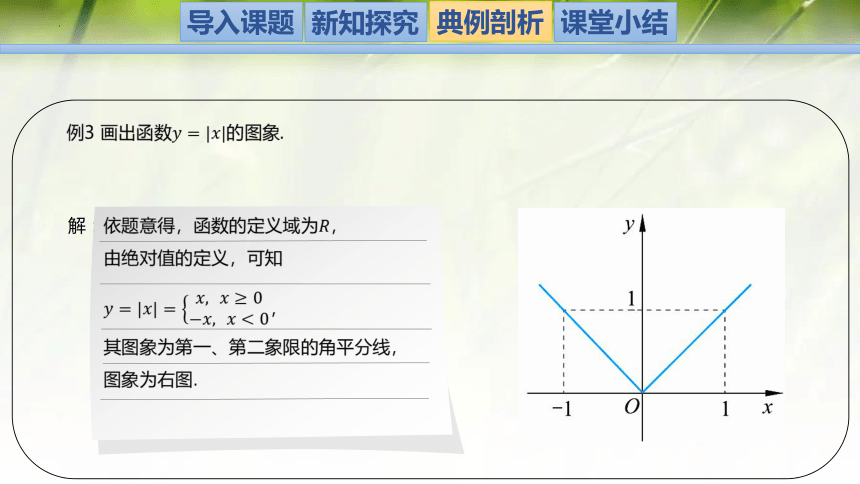
例3 画出函数的图象.
解:
依题意得,函数的定义域为,
由绝对值的定义,可知
,
其图象为第一、第二象限的角平分线,
图象为右图.
导入课题
新知探究
典例剖析
课堂小结
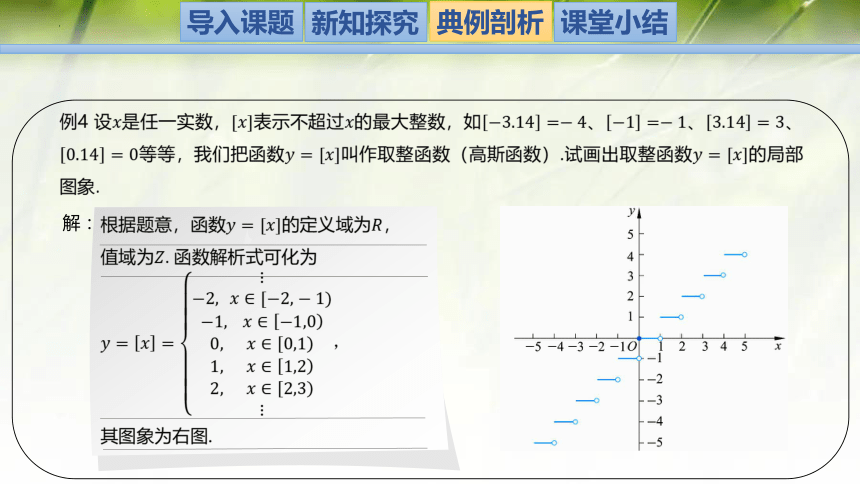
例4 设是任一实数,表示不超过的最大整数,如、、、等等,我们把函数叫作取整函数(高斯函数).试画出取整函数的局部图象.
解:
根据题意,函数的定义域为,
值域为.函数解析式可化为
,
其图象为右图.
导入课题
新知探究
典例剖析
课堂小结
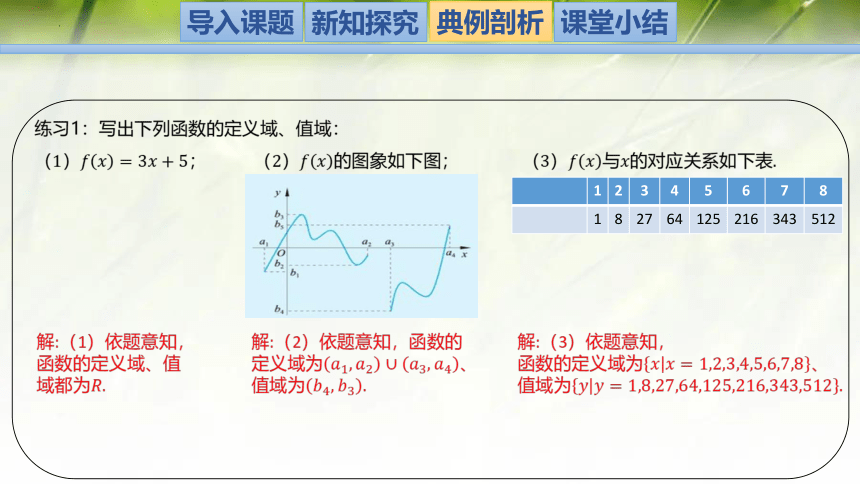
练习1:写出下列函数的定义域、值域:
(1); (2)的图象如下图; (3)与的对应关系如下表.
解:(1)依题意知,
函数的定义域、值
域都为.
1 2 3 4 5 6 7 8
1 8 27 64 125 216 343 512
解:(2)依题意知,函数的
定义域为、
值域为.
解:(3)依题意知,
函数的定义域为、
值域为.
导入课题
新知探究
典例剖析
课堂小结
练习2:下表列出的是一份数学测试选择题的答案表.
它是使用列表法表示的函数吗?为什么?
解:该答题表不是使用列表法表示的函数.
因为函数研究的自变量和因变量必须属于非空数集,而“正确答案”不是数集.
所以题号与正确答案之间不是函数关系.
题号 13 14 15 16
正确答案 C A D D
导入课题
新知探究
典例剖析
课堂小结
练习3:下图是某地区入学考试中一道满分为12分试题的成绩分布,这个图是用图像法表示的函
数吗?为什么?
解:该答题表是使用图象法表示的函数.
因为由图象可知,对于变量(分数)的每一个值,都有唯一确定的变量(人数)与之对应.
导入课题
新知探究
典例剖析
课堂小结
练习4:收集一些用列表法表示的函数.(课后自行收集)
练习5:如图,△ABC是一个等腰直角三角形,AB=AC=1,点E,F分别在边AB和AC上,且EF//BC,
点E从点A开始沿线段AB向B运动,写出点A到线段EF的距离d与线段EF的长度l之间的函数解析式,
并画出函数图象.
解:因为△ABC是等腰直角三角形,且AB=AC,
所以点A到EF的距离d等于EF的一半,
所以.
导入课题
新知探究
典例剖析
课堂小结
思考1:根据条件,求函数解析式.
①;②;
③已知是一元二次函数,且满足;.
解:(1) 设,则,
得
所以;
(2) 设,则,得,
则
所以;
导入课题
新知探究
典例剖析
课堂小结
思考1:根据条件,求函数解析式.
①;②;
③已知是一元二次函数,且满足;.
解:(3) 设,由,则,即,
又,即,
得,
则,解得,
所以.
导入课题
新知探究
典例剖析
课堂小结
思考2:若函数的定义域为,值域为,求实数的取值范围.
解:作出一元二次函数的图象.
抛物线对称轴,函数的最小值,如图,
所以实数的取值范围.
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
一种思想
换元的数学思想方法
一种函数
取整函数
三种表示法
解析法
列表法
图像法
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:课本P56 A组T3
作业2:课本P57 B组T2T3
谢谢聆听!
2.2函数的表示法
北师大版(2019)高中数学必修第一册
第二章 函数
第2节 函数
导入课题
新知讲授
典例剖析
课堂小结
初中我们学习了三种重要的函数类型,
一次函数
二次函数
反比例函数
三个函数都是用解析法表示的函数,在初中,我们就学习了三种函数的
表示方法:解析法、列表法、图像法,不同的问题适用不同的表示方法,因此,
今天我们要更加深入地学习函数的表示法.
一、函数的表示法
导入课题
解析法:用一个等式来表示变量之间的函数对应关系的方法叫作解析法.
这个等式叫做函数的解析式.
优点:变量之间的关系明确,便于精确计算,
例如,初中学习的一次函数,一元二次函数,反比例函数等都是用解析法表示的.
缺点:不够直观,某些函数无法用解析式表示.
例如,下图(心电图)
强度是时间的函数,但是我们没法用精确的解析式把函数表示出来.
列表法:用表格给出变量之间的函数对应关系的方法叫作列表法.
优点:列表法直接通过表格读数,不必通过计算,就表示出了两个变量之间的对应值,非常直观.
缺点:任何一个表格内标出的数都是有限个,也就只能表示有限个数值之间的函数关系.
新知探究
典例剖析
课堂小结
一、函数的表示法
导入课题
图象法:用图形给出变量之间的函数对应关系的方法叫作图象法.
优点:能直观地显示出变量的关系、变化规律和函数的性质,弥补了数、式的枯燥与抽象,是“数形
结合”思想方法的主要内容之一,不仅在研究函数中经常使用,在日常生活中用途也非常广泛.
缺点:无法进行精确运算,并非所有的函数都能用图像法表示.
例如,只有函数图象时,很多时候无法求出函数定义域、求精确的函数值等.
例如,狄利克雷函数,无法用图像法表示.
为了清楚地表示一个函数关系,需要有针对性地选择适当的表示方法,有时需要多种方法综合运用.
在实际问题中,还常常需要把函数的某种表示方法转化为另一种表示方法,这样才可以更清楚、全
面的了解函数的性质.
新知探究
典例剖析
课堂小结
导入课题
新知探究
典例剖析
课堂小结
例3 画出函数的图象.
解:
依题意得,函数的定义域为,
由绝对值的定义,可知
,
其图象为第一、第二象限的角平分线,
图象为右图.
导入课题
新知探究
典例剖析
课堂小结
例4 设是任一实数,表示不超过的最大整数,如、、、等等,我们把函数叫作取整函数(高斯函数).试画出取整函数的局部图象.
解:
根据题意,函数的定义域为,
值域为.函数解析式可化为
,
其图象为右图.
导入课题
新知探究
典例剖析
课堂小结
练习1:写出下列函数的定义域、值域:
(1); (2)的图象如下图; (3)与的对应关系如下表.
解:(1)依题意知,
函数的定义域、值
域都为.
1 2 3 4 5 6 7 8
1 8 27 64 125 216 343 512
解:(2)依题意知,函数的
定义域为、
值域为.
解:(3)依题意知,
函数的定义域为、
值域为.
导入课题
新知探究
典例剖析
课堂小结
练习2:下表列出的是一份数学测试选择题的答案表.
它是使用列表法表示的函数吗?为什么?
解:该答题表不是使用列表法表示的函数.
因为函数研究的自变量和因变量必须属于非空数集,而“正确答案”不是数集.
所以题号与正确答案之间不是函数关系.
题号 13 14 15 16
正确答案 C A D D
导入课题
新知探究
典例剖析
课堂小结
练习3:下图是某地区入学考试中一道满分为12分试题的成绩分布,这个图是用图像法表示的函
数吗?为什么?
解:该答题表是使用图象法表示的函数.
因为由图象可知,对于变量(分数)的每一个值,都有唯一确定的变量(人数)与之对应.
导入课题
新知探究
典例剖析
课堂小结
练习4:收集一些用列表法表示的函数.(课后自行收集)
练习5:如图,△ABC是一个等腰直角三角形,AB=AC=1,点E,F分别在边AB和AC上,且EF//BC,
点E从点A开始沿线段AB向B运动,写出点A到线段EF的距离d与线段EF的长度l之间的函数解析式,
并画出函数图象.
解:因为△ABC是等腰直角三角形,且AB=AC,
所以点A到EF的距离d等于EF的一半,
所以.
导入课题
新知探究
典例剖析
课堂小结
思考1:根据条件,求函数解析式.
①;②;
③已知是一元二次函数,且满足;.
解:(1) 设,则,
得
所以;
(2) 设,则,得,
则
所以;
导入课题
新知探究
典例剖析
课堂小结
思考1:根据条件,求函数解析式.
①;②;
③已知是一元二次函数,且满足;.
解:(3) 设,由,则,即,
又,即,
得,
则,解得,
所以.
导入课题
新知探究
典例剖析
课堂小结
思考2:若函数的定义域为,值域为,求实数的取值范围.
解:作出一元二次函数的图象.
抛物线对称轴,函数的最小值,如图,
所以实数的取值范围.
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
一种思想
换元的数学思想方法
一种函数
取整函数
三种表示法
解析法
列表法
图像法
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:课本P56 A组T3
作业2:课本P57 B组T2T3
谢谢聆听!
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
