《高考快车道》2026版高三一轮总复习(数学)15 第二章 第7课时 对数与对数函数
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习(数学)15 第二章 第7课时 对数与对数函数 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 11:49:17 | ||
图片预览











文档简介
(共87张PPT)
第二章
函数的概念与性质
第7课时 对数与对数函数
[考试要求] 1.理解对数的概念及运算性质,能用换底公式将一般对数转化成自然对数或常用对数.
2.通过实例,了解对数函数的概念,会画对数函数的图象,理解对数函数的单调性与特殊点.
3.了解指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数.
链接教材·夯基固本
1.对数的概念
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作__________,其中___叫做对数的底数,___叫做真数.
以____为底的对数叫做常用对数,log10N记为_______.
以___为底的对数叫做自然对数,logeN记为_______.
x=logaN
a
N
10
lg N
e
ln N
2.对数的性质与运算性质
(1)对数的性质:loga1=___,logaa=___(a>0,且a≠1).
(2)对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
①loga(MN)=______________;
②loga=______________;
③logaM n=________(n∈R).
0
1
logaM+logaN
logaM-logaN
nlogaM
(3)对数恒等式:=___(a>0,且a≠1,N>0).
(4)对数换底公式:logab=.
N
3.对数函数
(1)一般地,函数__________(a>0,且a≠1)叫做对数函数,其中x是自变量,定义域是_____________.
y=logax
(0,+∞)
(2)对数函数的图象与性质
项目 a>1 0图象
定义域 _____________
值域 R
性质 过定点__________,即x=1时,y=0
当x>1时,______; 当01时,______;
当0在(0,+∞)上是____函数 在(0,+∞)上是____函数
(0,+∞)
(1,0)
y>0
y<0
y<0
y>0
增
减
4.反函数
指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的图象关于直线______对称.
y=x
[常用结论]
1.换底公式的三个重要结论
(3)logab·logbc·logcd=logad.
(a>0,且a≠1;b>0,且b≠1;c>0,且c≠1;d>0;m≠0)
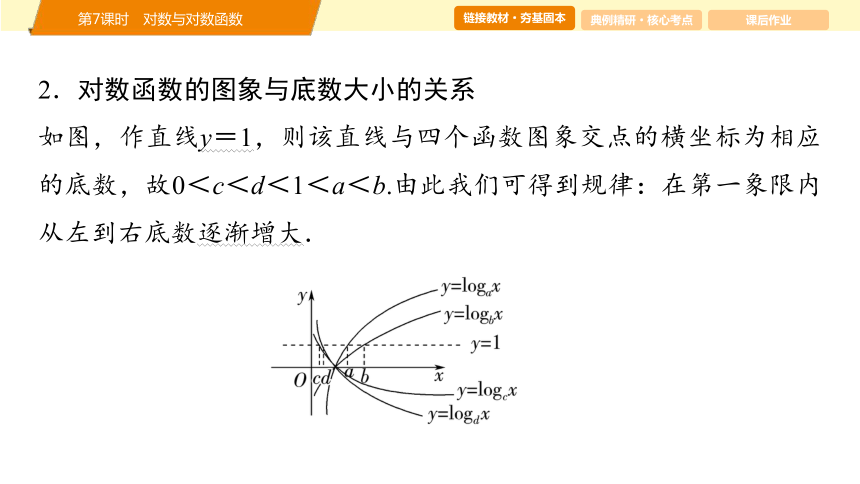
2.对数函数的图象与底数大小的关系
如图,作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数,故0<c<d<1<a<b.由此我们可得到规律:在第一象限内从左到右底数逐渐增大.
一、易错易混辨析(正确的打“√”,错误的打“×”)
(1)log2x2=2log2x. ( )
(2)函数y=log2(x+1)是对数函数. ( )
(3)函数y=ln 与y=ln (1+x)-ln(1-x)的定义域相同. ( )
(4)函数y=log2x与y=的图象重合. ( )
×
×
√
√
二、教材经典衍生
1.(人教A版必修第一册P140习题4.4T1改编)函数y=的定义域是________.
[由≥0,得0<2x-1≤1,
所以<x≤1.
所以函数y=的定义域是.]
2.(人教A版必修第一册P135练习T2改编)比较下列两个值的大小:
(1)log56________log54;
(2)log2________.
>
=
3.(人教A版必修第一册P126练习T3(2)改编)(log43+log83)×log32=________.
[(log43+log83)×log32==.]
4.(人教A版必修第一册P141习题4.4T12改编)若loga<1,则实数a的取值范围是________________________.
∪(1,+∞) [当a>1时,满足条件;
当0综上,a的取值范围是∪(1,+∞).]
∪(1,+∞)
考点一 对数的运算
[典例1] (1)(2025·四川成都模拟)若实数m,n,t满足5m=7n=t且=2,则t=( )
A.2 B.12 C. D.
(2)化简:(log62)2+log62×log63+2log63-=________.
(3)(2025·八省联考)已知函数f (x)=ax(a>0,a≠1),若f (ln 2)f (ln 4)=8,则a=________.
典例精研·核心考点
√
-log62
e
(1)D (2)-log62 (3)e [(1)因为5m=7n=t且=2,
易知t>0且t≠1,所以m=log5t,n=log7t,
所以=logt5,=logt7,
所以=logt5+logt7=logt35=2,则t=.故选D.
(2)(log62)2+log62×log63+2log63-
=log62×(log62+log63)+2log63-2
=log62+2log63-2=2(log62+log63)-log62-2
=2-log62-2=-log62.
(3)因为f (ln 2)=aln 2,f (ln 4)=aln 4,所以f (ln 2)f (ln 4)=aln 2·aln 4=aln 2+ln 4=a3ln 2=(aln 2)3=8,所以aln 2=2,所以a=e.]
名师点评 解决对数运算问题的常用方法
(1)将真数化为底数的指数幂的形式进行化简.
(2)将同底对数的和、差、倍合并.
(3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底公式的正用、逆用及变形应用.
[跟进训练]
1.(1)(2025·天津武清模拟)设a=lg 20+lg ,b=log95,则a+3b的值为( )
A.2+ B.1+ C.27 D.26
(2)(2024·全国甲卷)已知a>1且=-,则a=________.
(3)计算:lg 25+lg 2×lg 50+(lg 2)2=________.
√
64
2
(1)B (2)64 (3)2 [(1)根据题意,
a+3b=lg 20+lg+=lg+lg+
=lg()+=lg 10+=1+.故选B.
(2)由题意=log2a=-,整理得(log2a)2-5log2a-6=0,
解得log2a=-1或log2a=6.又a>1,
所以log2a=6=log226,故a=26=64.
(3)原式=2lg 5+lg 2(1+lg 5)+(lg 2)2
=2lg 5+lg 2+lg 2×lg 5+(lg 2)2
=1+lg 5+lg 2(lg 5+lg 2)
=1+lg 5+lg 2=1+lg 10=2.]
考点二 对数函数的图象及应用
[典例2] (1)已知函数f (x)=loga(2x+b-1)(a>0,且a≠1)的图象如图所示,则a,b满足的关系是( )
A.0C.0(2)当0<x≤时,4x<logax,则a的取值范围是( )
A. B.
C.(1,) D.(,2)
√
√
(1)A (2)B [(1)由函数图象可知,f (x)为增函数,故a>1.
函数图象与y轴的交点坐标为(0,logab),
由函数图象可知-1综上,0(2)构造函数f (x)=4x和g(x)=logax,当a>1时,不满足条件;当0<a<1时,在同一直角坐标系中画出两个函数大致的图象,如图所示,由题意可知
f <g,即2<loga,
则a>,所以a的取值范围为.]
[拓展变式] 将本例(2)中“4x<logax”变为“关于x的方程4x=logax有解”,则a的取值范围是________.
[若方程4x=logax在上有解,则函数y=4x的图象和函数y=logax的图象在上有交点.
由图象可知解得0<a≤.]
名师点评 对数函数图象的识别及应用方法
(1)在识别函数图象时,要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.
(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.
[跟进训练]
2.(1)(2024·广东深圳二模)已知a>0,且a≠1,则函数y=loga的图象一定经过( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
(2)已知函数f (x)=|ln x|,若0√
(3,+∞)
(1)D (2)(3,+∞) [(1)当x=0时,y=loga=-1,
则当0则当a>1时,函数图象过第一、三、四象限;
所以函数y=loga的图象一定经过第三、四象限.
故选D.
(2)f (x)=|ln x|的图象如图所示,
因为f (a)=f (b),所以|ln a|=|ln b|,
因为00,
所以01,所以-ln a=ln b,
所以ln a+ln b=ln (ab)=0,
所以ab=1,则b=,所以a+2b=a+,
令g(x)=x+(0所以g(x)>g(1)=1+2=3,所以a+2b>3,
所以a+2b的取值范围为(3,+∞).]
【教用·备选题】
(多选)若函数f (x)=ax-2,g(x)=loga|x|,其中a>0,且a≠1,则函数
f (x),g(x)在同一平面直角坐标系中的大致图象可能是( )
A B
C D
√
√
AD [易知g(x)=loga|x|为偶函数.当0<a<1时,f (x)=ax-2单调递减,g(x)=loga|x|在(0,+∞)上单调递减,此时A选项符合题意.当a>1时,f (x)=ax-2单调递增,g(x)=loga|x|在(0,+∞)上单调递增,此时D选项符合题意.故选AD.]
考点三 对数函数的性质及应用
考向1 比较大小
[典例3] 已知a=log2e,b=ln 2,c=,则a,b,c的大小关系为( )
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
√
D [法一(中间量法、性质法):因为a=log2e>1,b=ln 2∈(0,1),所以a>b.又因为c==log23,且函数y=log2x在(0,+∞)上单调递增,所以log23>log2e,所以c>a,所以c>a>b.
法二(图象法):=log23,在同一平面直角坐标系中画出函数y=log2x,y=ln x的图象,
如图,由图可知c>a>b.]
考向2 解与对数有关的不等式
[典例4] (1)已知函数f (x)是定义在R上的偶函数,且在[0,+∞)上单调递增.若正实数a满足f (log2a)+≤2f (1),则a的取值范围是( )
A.[1,2] B.
C. D.(0,2]
√
(2)设函数f (x)=若f (a)>f (-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
√
(1)C (2)C [(1)因为=-log2a,所以f (log2a)+=
f (log2a)+f (-log2a)=2f (log2a),原不等式变为2f (log2a)≤2f (1),即f (log2a)≤f (1).又因为f (x)是定义在R上的偶函数,且在[0,+∞)上单调递增,所以|log2a|≤1,即-1≤log2a≤1,解得≤a≤2,故选C.
(2)由题意可得
或
解得a>1或-1考向3 对数函数性质的综合应用
[典例5] (1)(多选)(2025·广东深圳中学模拟)已知函数f (x)=lg (x2+ax-a-1),给出下述论述,其中正确的是( )
A.当a=0时,f (x)的定义域为(-∞,-1)∪(1,+∞)
B.f (x)一定有最小值
C.当a=0时,f (x)的值域为R
D.若f (x)在区间[2,+∞)上单调递增,则实数a的取值范围是{a|a≥-4}
√
√
(2)(多选)已知函数f (x)=ln ,下列说法正确的是( )
A.f (x)为奇函数
B.f (x)为偶函数
C.f (x)在上单调递减
D.f (x)的值域为(-∞,0)∪(0,+∞)
(3)已知函数f=ln -x是偶函数,则实数a的值为________.
√
√
√
2
(1)AC (2)ACD (3)2 [(1)对于A,∵a=0,∴f (x)=lg (x2-1),即x2-1>0,∴x<-1或x>1,∴A正确;
对于B,令u(x)=x2+ax-a-1,则复合函数y=f (x)是由y=lg u,u=x2+ax-a-1复合而成的,
∵y=lg u在定义域内是单调递增的,而u=x2+ax-a-1(u>0)无最小值,∴f (x)没有最小值,∴B错误;
对于C,当a=0时,f (x)=lg (x2-1)中的u=x2-1中的u能够取到所有的正数,∴f (x)的值域为R,∴C正确;
对于D,∵复合函数y=lg (x2+ax-a-1)是由y=lg u,u=x2+ax-a-1复合而成的,而y=lg u在定义域内是单调递增的,又∵y=f (x)在区间[2,+∞)上单调递增,由复合函数的单调性可知,u=x2+ax-a-1在区间[2,+∞)上单调递增,则有-≤2,
即a≥-4.
又∵x2+ax-a-1>0在区间[2,+∞)上恒成立,则有22+2a-a-1>0,即a>-3,
∴a>-3,∴D错误.故选AC.
(2)令>0,解得x>或x<-,
∴f (x)的定义域为,
又f (-x)=ln =ln =ln
=-ln =-f (x),
∴f (x)为奇函数,故A正确,B错误.
又f (x)=ln =ln ,
令t=1+,t>0且t≠1,则y=ln t,
又t=1+在上单调递减,且y=ln t为增函数,
∴f (x)在上单调递减,故C正确;
由C分析可得f (x)的值域是(-∞,0)∪(0,+∞),故D正确.
(3)由题意知f (x)的定义域为R,函数f =ln -x是偶函数,则f=ln +x=f=ln -x,
即ln =2x,化简得ln eax=2x,解得a=2.]
【教用·备选题】
1.若f (x)=lg (x2-2ax+1+a)在(-∞,1]上单调递减,则a的取值范围为( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)
√
A [令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,则图象的对称轴为x=a,要使函数f (x)在(-∞,1]上单调递减,则有即解得1≤a<2,即a∈[1,2).]
2.若实数a,b,c满足loga2( )
A.aC.cC [根据不等式的性质和对数的换底公式可得
<<<0,即log2c√
名师点评 求与对数函数有关的复合函数的单调性、值域问题,必须弄清三个问题:一是定义域;二是底数与1的大小关系;三是复合函数的构成.
[跟进训练]
3.(1)设a=log412,b=log515,c=log618,则( )
A.a>b>c B.b>c>a
C.a>c>b D.c>b>a
(2)已知函数f (x)=ln (-x)+2,则f (lg 3)+f=________.
(3)已知f (x)=1+log3x(1≤x≤9),设函数g(x)=[f (x)]2+f (x2),则g(x)max-g(x)min=________.
√
4
5
(1)A (2)4 (3)5 [(1)a=1+log43,b=1+log53,c=1+log63,∵log43>log53>log63,∴a>b>c.
(2)设g(x)=ln (-x),则f (x)=g(x)+2,显然有g(-x)=-g(x),即g(x)为奇函数,则g(-x)+g(x)=0,所以f (lg 3)+f=f (lg 3)+f (-lg 3)=g(lg 3)+2+g(-lg 3)+2=4.
(3)由题意得
∴1≤x≤3,∴g(x)的定义域为[1,3],
g(x)=[f (x)]2+f (x2)
=(1+log3x)2+1+log3x2
=(log3x)2+4log3x+2,
设t=log3x,则0≤t≤1,
则y=t2+4t+2=(t+2)2-2在[0,1]上单调递增,
∴当t=0,即x=1时,g(x)min=g(1)=2,
当t=1,即x=3时,g(x)max=g(3)=7,
∴g(x)max-g(x)min=5.]
【教用·备选题】
1.(多选)(2025·山西忻州模拟)已知x>0,y>0,且x-y>ln ,则
( )
A.x>y B.x+>y+
C.ln (x-y)<0 D.<2-y
√
√
√
ABD [因为x-y>ln ,所以x-y>ln y-ln x,
所以ln x+x>ln y+y.
对于A,设f (x)=ln x+x,则f (x)在(0,+∞)上单调递增,因为ln x+x>
ln y+y,所以f (x)>f (y),
所以x>y,故A正确;
对于B,因为x>0,y>0,且x>y,
所以<,所以x+>y+,故B正确;
对于C,当x-y=e时,ln (x-y)=1,故C错误;
对于D,因为x>y,所以-x<-y,
所以2-x<2-y,即<2-y,故D正确.故选ABD.]
2.(多选)(2025·浙江杭州模拟)已知函数f (x)=ln (x2+x+m) (m∈R),则( )
A.当m>时,f (x)的定义域为R
B.f (x)一定存在最小值
C.f (x)的图象关于直线x=-对称
D.当m≥1时,f (x)的值域为R
√
√
AC [对于A,若m>,则Δ=1-4m<0,则x2+x+m>0恒成立,所以
f (x)的定义域为R,故A正确;
对于B,若m=0,则f (x)=ln (x2+x)的定义域为(-∞,-1)∪(0,
+∞),值域为R,没有最小值,故B错误;
对于C,由于函数y=ln 为偶函数,其图象关于y轴对称,
将该函数的图象向左平移个单位长度即可得到函数f (x)=ln =ln (x2+x+m)的图象,
此时f (x)的图象的对称轴为直线x=-,故C正确;
对于D,若m≥1,则y=x2+x+m=+m-,故f (x)的值域不是R,故D错误.
故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
一、单项选择题
1.若xlog34=1,则4x+4-x的值为( )
A. B.3 C.4 D.
13
课后作业(十三) 对数与对数函数
√
A [∵xlog34=1,∴log34x=1,∴4x=3,
∴4x+4-x=3+3-1=.故选A.]
2.若函数f (x)=loga(x+b)(a>0且a≠1,b∈R)的大致图象如图所示,则函数g(x)=a-x-b的大致图象是( )
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
√
A B
C D
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
C [根据函数f (x)=loga(x+b)的图象,可得03.(2024·天津滨海新区三模)已知a=,b=log0.42,c=,则( )
A.a>b>c B.b>a>c
C.c>a>b D.a>c>b
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
13
C [a==0.4,
b=log0.420=log0.311,
故c>a>b.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
4.(2024·江苏宿迁三模)已知函数f (x)为R上的奇函数,且当x>0时,f (x)=log2x-1,则f (-)=( )
A. B.- C. D.-
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
13
A [f (-1=-1=-1=-,
因为f (x)为R上的奇函数,所以f (-)=.
故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·辽宁丹东期末)已知函数f (x)=logax(a>0,a≠1)与g(x)的图象关于直线y=x对称,且g(-1)=,则函数y=loga(x2-2x)的单调递减区间是( )
A.(-∞,1) B.(1,+∞)
C.(-∞,0) D.(2,+∞)
13
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为函数f (x)=logax(a>0,a≠1)与g(x)的图象关于直线y=x对称,所以g(x)=ax(a>0,a≠1),
因为g(-1)=,所以=a-1,解得a=3.
所以y=loga(x2-2x)=log3(x2-2x),
由x2-2x>0,可得y=log3(x2-2x)的定义域为(-∞,0)∪(2,+∞),
令t=x2-2x,则t=x2-2x在(-∞,0)上单调递减,
而y=log3t在定义域上单调递增,
由复合函数的单调性可知,y=log3(x2-2x)在(-∞,0)上单调递减.故选C.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.若函数f (x)=loga在区间内恒有f (x)>0,则f (x)的单调递增区间为( )
A.(0,+∞) B.(2,+∞)
C.(1,+∞) D.
13
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [令M=x2+x,故x∈时,M∈(1,+∞),恒有f (x)>0,所以a>1,所以函数y=logaM为增函数,又M=-,所以M的单调递增区间为.又x2+x>0,所以x>0或x<-,所以函数f (x)的单调递增区间为(0,+∞).故选A.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
二、多项选择题
7.(2025·河南郑州模拟)关于函数f (x)=log3,下列结论正确的是( )
A.定义域为(-∞,-1)∪(3,+∞)
B.f (x)是偶函数
C.f (x)的图象关于点(1,0)对称
D.f (x)在(3,+∞)上单调递增
13
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
ACD [对于A,由>0得x<-1或x>3,故定义域为(-∞,-1) ∪(3,+∞),A正确;
对于B,因为定义域不关于原点对称,故f (x)不是偶函数,B错误;
对于C,因为f (1-x)+f (1+x)=log3+log3
=log3+log3=log3=log31=0,
所以f (x)的图象关于点(1,0)对称,C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
对于D,f (x)=log3=log3,
因为函数t=1-在区间(3,+∞)上单调递增,且y=log3t在(0,
+∞)上单调递增,
所以f (x)在(3,+∞)上单调递增,D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2025·湖北重点高中联考)已知实数x,y,z满足2x=3,3y=4,4z=5,则下列结论正确的是( )
A.y< B.xyz>2
C.y2
13
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [因为2x=3,3y=4,4z=5,
所以x=log23,y=log34,z=log45,
对于A,因为43<34,则log343所以y=log34<,故A正确;
对于B,xyz=log23·log34·log45=log25>log24=2,故B正确;
对于C,y-z=log34-log45==,
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
因为0所以lg 3lg 5<=,
又(lg 4)2==>,
所以(lg 4)2-lg 3lg 5>0,即y-z>0,所以y>z,故C错误;
对于D,因为x=log23>1,y=log34>1,
所以x+y=log23+log34>2=2=2,故D正确.故选ABD.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
三、填空题
9.(2024·河南郑州三模)已知logab+4logba=4,则的值为________.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[因为logab+4logba=4,
所以logab+=4,可得 (logab)2-4logab+4=0,
即(logab-2)2=0,所以logab=2,即a2=b,
所以==.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·安徽宣城模拟)已知实数x满足不等式2(log2x)2-5log2x+2≤0,则函数f (x)=log2·log2的最大值是________.
13
[由2(log2x)2-5log2x+2≤0,
解得≤log2x≤2,
f (x)=log2·log2=(log2x-1)(log2x-2)=-,
当log2x=时,f (x)取得最大值.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
四、解答题
11.已知f (x)=.
(1)若a=2,求f (x)的值域;
(2)若f (x)在(1,+∞)上单调递减,求a的取值范围.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)当a=2时,f (x)=,
令t=x2-2x+10=(x-1)2+9,
=-2,
∴f (x)的值域为(-∞,-2].
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)令u=x2-ax+5a,
∵y=为减函数,f (x)在(1,+∞)上单调递减,
∴u=x2-ax+5a在(1,+∞)上单调递增,
∴解得-≤a≤2,
∴a的取值范围是.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·江苏盐城模拟)已知函数f (x)=log4.
(1)解关于x的不等式f (x)>3;
(2)若存在x∈[2,4],使得不等式f (2x)-a·log2x+1≥0成立,求实数a的取值范围.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为f (x)的定义域为(0,+∞),则
f (x)=log2·2log2=(log2x-2)(log2x-4)=(log2x)2-6log2x+8,
设log2x=t(t∈R),则不等式可化为t2-6t+8>3,
即t2-6t+5>0,
解得t<1或t>5,即log2x<1或log2x>5,
解得032.
所以不等式的解集为{x|032}.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为f (2x)-a·log2x+1≥0,
所以(log2x-1)·(log2x-3)-alog2x+1≥0,
设log2x=t,则t∈[1,2],
原问题化为:存在t∈[1,2],t2-4t+4-at≥0.
即a≤t+-4在t∈[1,2]上有解.
因为y=t+-4在[1,2]上单调递减,
所以=1,所以a≤1.
即实数a的取值范围是(-∞,1].
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
13.已知函数f (x)=2lg (10x+a)-x,a∈R.
(1)当a=1时,判断函数f (x)的奇偶性并证明;
(2)给定实数a>0且a≠1,问是否存在直线x=x0,使得函数f (x)的图象关于直线x=x0对称?若存在,求出x0的值(用a表示);若不存在,请说明理由.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)当a=1时,f (x)=2lg (10x+1)-x,
函数f (x)为偶函数,证明如下:
∵f (-x)=2lg (10-x+1)-(-x)=2lg +x=2lg (1+10x)-
2lg (10x)+x=2lg (10x+1)-x=f (x),
又函数的定义域为R,∴函数f (x)为偶函数.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)假设存在直线x=x0,使得函数f (x)的图象关于直线x=x0对称,则
f (x0+x)=f (x0-x),
∴2lg (+a)-(x0+x)=2lg (+a)-(x0-x),
即lg (+a)-lg (+a)=x,
即lg =x,∴=10x,
即+a=10x(+a)=+a·10x,
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
)=0,
=0,即a=,
∵a>0且a≠1,
∴x0=lg a,
故存在x0=lg a,使得函数f (x)的图象关于直线x=x0对称.
13
谢 谢!
第二章
函数的概念与性质
第7课时 对数与对数函数
[考试要求] 1.理解对数的概念及运算性质,能用换底公式将一般对数转化成自然对数或常用对数.
2.通过实例,了解对数函数的概念,会画对数函数的图象,理解对数函数的单调性与特殊点.
3.了解指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数.
链接教材·夯基固本
1.对数的概念
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作__________,其中___叫做对数的底数,___叫做真数.
以____为底的对数叫做常用对数,log10N记为_______.
以___为底的对数叫做自然对数,logeN记为_______.
x=logaN
a
N
10
lg N
e
ln N
2.对数的性质与运算性质
(1)对数的性质:loga1=___,logaa=___(a>0,且a≠1).
(2)对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
①loga(MN)=______________;
②loga=______________;
③logaM n=________(n∈R).
0
1
logaM+logaN
logaM-logaN
nlogaM
(3)对数恒等式:=___(a>0,且a≠1,N>0).
(4)对数换底公式:logab=.
N
3.对数函数
(1)一般地,函数__________(a>0,且a≠1)叫做对数函数,其中x是自变量,定义域是_____________.
y=logax
(0,+∞)
(2)对数函数的图象与性质
项目 a>1 0
定义域 _____________
值域 R
性质 过定点__________,即x=1时,y=0
当x>1时,______; 当0
当0
(0,+∞)
(1,0)
y>0
y<0
y<0
y>0
增
减
4.反函数
指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的图象关于直线______对称.
y=x
[常用结论]
1.换底公式的三个重要结论
(3)logab·logbc·logcd=logad.
(a>0,且a≠1;b>0,且b≠1;c>0,且c≠1;d>0;m≠0)
2.对数函数的图象与底数大小的关系
如图,作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数,故0<c<d<1<a<b.由此我们可得到规律:在第一象限内从左到右底数逐渐增大.
一、易错易混辨析(正确的打“√”,错误的打“×”)
(1)log2x2=2log2x. ( )
(2)函数y=log2(x+1)是对数函数. ( )
(3)函数y=ln 与y=ln (1+x)-ln(1-x)的定义域相同. ( )
(4)函数y=log2x与y=的图象重合. ( )
×
×
√
√
二、教材经典衍生
1.(人教A版必修第一册P140习题4.4T1改编)函数y=的定义域是________.
[由≥0,得0<2x-1≤1,
所以<x≤1.
所以函数y=的定义域是.]
2.(人教A版必修第一册P135练习T2改编)比较下列两个值的大小:
(1)log56________log54;
(2)log2________.
>
=
3.(人教A版必修第一册P126练习T3(2)改编)(log43+log83)×log32=________.
[(log43+log83)×log32==.]
4.(人教A版必修第一册P141习题4.4T12改编)若loga<1,则实数a的取值范围是________________________.
∪(1,+∞) [当a>1时,满足条件;
当0
∪(1,+∞)
考点一 对数的运算
[典例1] (1)(2025·四川成都模拟)若实数m,n,t满足5m=7n=t且=2,则t=( )
A.2 B.12 C. D.
(2)化简:(log62)2+log62×log63+2log63-=________.
(3)(2025·八省联考)已知函数f (x)=ax(a>0,a≠1),若f (ln 2)f (ln 4)=8,则a=________.
典例精研·核心考点
√
-log62
e
(1)D (2)-log62 (3)e [(1)因为5m=7n=t且=2,
易知t>0且t≠1,所以m=log5t,n=log7t,
所以=logt5,=logt7,
所以=logt5+logt7=logt35=2,则t=.故选D.
(2)(log62)2+log62×log63+2log63-
=log62×(log62+log63)+2log63-2
=log62+2log63-2=2(log62+log63)-log62-2
=2-log62-2=-log62.
(3)因为f (ln 2)=aln 2,f (ln 4)=aln 4,所以f (ln 2)f (ln 4)=aln 2·aln 4=aln 2+ln 4=a3ln 2=(aln 2)3=8,所以aln 2=2,所以a=e.]
名师点评 解决对数运算问题的常用方法
(1)将真数化为底数的指数幂的形式进行化简.
(2)将同底对数的和、差、倍合并.
(3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底公式的正用、逆用及变形应用.
[跟进训练]
1.(1)(2025·天津武清模拟)设a=lg 20+lg ,b=log95,则a+3b的值为( )
A.2+ B.1+ C.27 D.26
(2)(2024·全国甲卷)已知a>1且=-,则a=________.
(3)计算:lg 25+lg 2×lg 50+(lg 2)2=________.
√
64
2
(1)B (2)64 (3)2 [(1)根据题意,
a+3b=lg 20+lg+=lg+lg+
=lg()+=lg 10+=1+.故选B.
(2)由题意=log2a=-,整理得(log2a)2-5log2a-6=0,
解得log2a=-1或log2a=6.又a>1,
所以log2a=6=log226,故a=26=64.
(3)原式=2lg 5+lg 2(1+lg 5)+(lg 2)2
=2lg 5+lg 2+lg 2×lg 5+(lg 2)2
=1+lg 5+lg 2(lg 5+lg 2)
=1+lg 5+lg 2=1+lg 10=2.]
考点二 对数函数的图象及应用
[典例2] (1)已知函数f (x)=loga(2x+b-1)(a>0,且a≠1)的图象如图所示,则a,b满足的关系是( )
A.0
A. B.
C.(1,) D.(,2)
√
√
(1)A (2)B [(1)由函数图象可知,f (x)为增函数,故a>1.
函数图象与y轴的交点坐标为(0,logab),
由函数图象可知-1
f <g,即2<loga,
则a>,所以a的取值范围为.]
[拓展变式] 将本例(2)中“4x<logax”变为“关于x的方程4x=logax有解”,则a的取值范围是________.
[若方程4x=logax在上有解,则函数y=4x的图象和函数y=logax的图象在上有交点.
由图象可知解得0<a≤.]
名师点评 对数函数图象的识别及应用方法
(1)在识别函数图象时,要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.
(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.
[跟进训练]
2.(1)(2024·广东深圳二模)已知a>0,且a≠1,则函数y=loga的图象一定经过( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
(2)已知函数f (x)=|ln x|,若0
(3,+∞)
(1)D (2)(3,+∞) [(1)当x=0时,y=loga=-1,
则当0
所以函数y=loga的图象一定经过第三、四象限.
故选D.
(2)f (x)=|ln x|的图象如图所示,
因为f (a)=f (b),所以|ln a|=|ln b|,
因为0
所以0
所以ln a+ln b=ln (ab)=0,
所以ab=1,则b=,所以a+2b=a+,
令g(x)=x+(0
所以a+2b的取值范围为(3,+∞).]
【教用·备选题】
(多选)若函数f (x)=ax-2,g(x)=loga|x|,其中a>0,且a≠1,则函数
f (x),g(x)在同一平面直角坐标系中的大致图象可能是( )
A B
C D
√
√
AD [易知g(x)=loga|x|为偶函数.当0<a<1时,f (x)=ax-2单调递减,g(x)=loga|x|在(0,+∞)上单调递减,此时A选项符合题意.当a>1时,f (x)=ax-2单调递增,g(x)=loga|x|在(0,+∞)上单调递增,此时D选项符合题意.故选AD.]
考点三 对数函数的性质及应用
考向1 比较大小
[典例3] 已知a=log2e,b=ln 2,c=,则a,b,c的大小关系为( )
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
√
D [法一(中间量法、性质法):因为a=log2e>1,b=ln 2∈(0,1),所以a>b.又因为c==log23,且函数y=log2x在(0,+∞)上单调递增,所以log23>log2e,所以c>a,所以c>a>b.
法二(图象法):=log23,在同一平面直角坐标系中画出函数y=log2x,y=ln x的图象,
如图,由图可知c>a>b.]
考向2 解与对数有关的不等式
[典例4] (1)已知函数f (x)是定义在R上的偶函数,且在[0,+∞)上单调递增.若正实数a满足f (log2a)+≤2f (1),则a的取值范围是( )
A.[1,2] B.
C. D.(0,2]
√
(2)设函数f (x)=若f (a)>f (-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
√
(1)C (2)C [(1)因为=-log2a,所以f (log2a)+=
f (log2a)+f (-log2a)=2f (log2a),原不等式变为2f (log2a)≤2f (1),即f (log2a)≤f (1).又因为f (x)是定义在R上的偶函数,且在[0,+∞)上单调递增,所以|log2a|≤1,即-1≤log2a≤1,解得≤a≤2,故选C.
(2)由题意可得
或
解得a>1或-1
[典例5] (1)(多选)(2025·广东深圳中学模拟)已知函数f (x)=lg (x2+ax-a-1),给出下述论述,其中正确的是( )
A.当a=0时,f (x)的定义域为(-∞,-1)∪(1,+∞)
B.f (x)一定有最小值
C.当a=0时,f (x)的值域为R
D.若f (x)在区间[2,+∞)上单调递增,则实数a的取值范围是{a|a≥-4}
√
√
(2)(多选)已知函数f (x)=ln ,下列说法正确的是( )
A.f (x)为奇函数
B.f (x)为偶函数
C.f (x)在上单调递减
D.f (x)的值域为(-∞,0)∪(0,+∞)
(3)已知函数f=ln -x是偶函数,则实数a的值为________.
√
√
√
2
(1)AC (2)ACD (3)2 [(1)对于A,∵a=0,∴f (x)=lg (x2-1),即x2-1>0,∴x<-1或x>1,∴A正确;
对于B,令u(x)=x2+ax-a-1,则复合函数y=f (x)是由y=lg u,u=x2+ax-a-1复合而成的,
∵y=lg u在定义域内是单调递增的,而u=x2+ax-a-1(u>0)无最小值,∴f (x)没有最小值,∴B错误;
对于C,当a=0时,f (x)=lg (x2-1)中的u=x2-1中的u能够取到所有的正数,∴f (x)的值域为R,∴C正确;
对于D,∵复合函数y=lg (x2+ax-a-1)是由y=lg u,u=x2+ax-a-1复合而成的,而y=lg u在定义域内是单调递增的,又∵y=f (x)在区间[2,+∞)上单调递增,由复合函数的单调性可知,u=x2+ax-a-1在区间[2,+∞)上单调递增,则有-≤2,
即a≥-4.
又∵x2+ax-a-1>0在区间[2,+∞)上恒成立,则有22+2a-a-1>0,即a>-3,
∴a>-3,∴D错误.故选AC.
(2)令>0,解得x>或x<-,
∴f (x)的定义域为,
又f (-x)=ln =ln =ln
=-ln =-f (x),
∴f (x)为奇函数,故A正确,B错误.
又f (x)=ln =ln ,
令t=1+,t>0且t≠1,则y=ln t,
又t=1+在上单调递减,且y=ln t为增函数,
∴f (x)在上单调递减,故C正确;
由C分析可得f (x)的值域是(-∞,0)∪(0,+∞),故D正确.
(3)由题意知f (x)的定义域为R,函数f =ln -x是偶函数,则f=ln +x=f=ln -x,
即ln =2x,化简得ln eax=2x,解得a=2.]
【教用·备选题】
1.若f (x)=lg (x2-2ax+1+a)在(-∞,1]上单调递减,则a的取值范围为( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)
√
A [令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,则图象的对称轴为x=a,要使函数f (x)在(-∞,1]上单调递减,则有即解得1≤a<2,即a∈[1,2).]
2.若实数a,b,c满足loga2
A.a
<<<0,即log2c
名师点评 求与对数函数有关的复合函数的单调性、值域问题,必须弄清三个问题:一是定义域;二是底数与1的大小关系;三是复合函数的构成.
[跟进训练]
3.(1)设a=log412,b=log515,c=log618,则( )
A.a>b>c B.b>c>a
C.a>c>b D.c>b>a
(2)已知函数f (x)=ln (-x)+2,则f (lg 3)+f=________.
(3)已知f (x)=1+log3x(1≤x≤9),设函数g(x)=[f (x)]2+f (x2),则g(x)max-g(x)min=________.
√
4
5
(1)A (2)4 (3)5 [(1)a=1+log43,b=1+log53,c=1+log63,∵log43>log53>log63,∴a>b>c.
(2)设g(x)=ln (-x),则f (x)=g(x)+2,显然有g(-x)=-g(x),即g(x)为奇函数,则g(-x)+g(x)=0,所以f (lg 3)+f=f (lg 3)+f (-lg 3)=g(lg 3)+2+g(-lg 3)+2=4.
(3)由题意得
∴1≤x≤3,∴g(x)的定义域为[1,3],
g(x)=[f (x)]2+f (x2)
=(1+log3x)2+1+log3x2
=(log3x)2+4log3x+2,
设t=log3x,则0≤t≤1,
则y=t2+4t+2=(t+2)2-2在[0,1]上单调递增,
∴当t=0,即x=1时,g(x)min=g(1)=2,
当t=1,即x=3时,g(x)max=g(3)=7,
∴g(x)max-g(x)min=5.]
【教用·备选题】
1.(多选)(2025·山西忻州模拟)已知x>0,y>0,且x-y>ln ,则
( )
A.x>y B.x+>y+
C.ln (x-y)<0 D.<2-y
√
√
√
ABD [因为x-y>ln ,所以x-y>ln y-ln x,
所以ln x+x>ln y+y.
对于A,设f (x)=ln x+x,则f (x)在(0,+∞)上单调递增,因为ln x+x>
ln y+y,所以f (x)>f (y),
所以x>y,故A正确;
对于B,因为x>0,y>0,且x>y,
所以<,所以x+>y+,故B正确;
对于C,当x-y=e时,ln (x-y)=1,故C错误;
对于D,因为x>y,所以-x<-y,
所以2-x<2-y,即<2-y,故D正确.故选ABD.]
2.(多选)(2025·浙江杭州模拟)已知函数f (x)=ln (x2+x+m) (m∈R),则( )
A.当m>时,f (x)的定义域为R
B.f (x)一定存在最小值
C.f (x)的图象关于直线x=-对称
D.当m≥1时,f (x)的值域为R
√
√
AC [对于A,若m>,则Δ=1-4m<0,则x2+x+m>0恒成立,所以
f (x)的定义域为R,故A正确;
对于B,若m=0,则f (x)=ln (x2+x)的定义域为(-∞,-1)∪(0,
+∞),值域为R,没有最小值,故B错误;
对于C,由于函数y=ln 为偶函数,其图象关于y轴对称,
将该函数的图象向左平移个单位长度即可得到函数f (x)=ln =ln (x2+x+m)的图象,
此时f (x)的图象的对称轴为直线x=-,故C正确;
对于D,若m≥1,则y=x2+x+m=+m-,故f (x)的值域不是R,故D错误.
故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
一、单项选择题
1.若xlog34=1,则4x+4-x的值为( )
A. B.3 C.4 D.
13
课后作业(十三) 对数与对数函数
√
A [∵xlog34=1,∴log34x=1,∴4x=3,
∴4x+4-x=3+3-1=.故选A.]
2.若函数f (x)=loga(x+b)(a>0且a≠1,b∈R)的大致图象如图所示,则函数g(x)=a-x-b的大致图象是( )
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
√
A B
C D
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
C [根据函数f (x)=loga(x+b)的图象,可得0
A.a>b>c B.b>a>c
C.c>a>b D.a>c>b
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
13
C [a==0.4,
b=log0.42
故c>a>b.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
4.(2024·江苏宿迁三模)已知函数f (x)为R上的奇函数,且当x>0时,f (x)=log2x-1,则f (-)=( )
A. B.- C. D.-
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
13
A [f (-1=-1=-1=-,
因为f (x)为R上的奇函数,所以f (-)=.
故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·辽宁丹东期末)已知函数f (x)=logax(a>0,a≠1)与g(x)的图象关于直线y=x对称,且g(-1)=,则函数y=loga(x2-2x)的单调递减区间是( )
A.(-∞,1) B.(1,+∞)
C.(-∞,0) D.(2,+∞)
13
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为函数f (x)=logax(a>0,a≠1)与g(x)的图象关于直线y=x对称,所以g(x)=ax(a>0,a≠1),
因为g(-1)=,所以=a-1,解得a=3.
所以y=loga(x2-2x)=log3(x2-2x),
由x2-2x>0,可得y=log3(x2-2x)的定义域为(-∞,0)∪(2,+∞),
令t=x2-2x,则t=x2-2x在(-∞,0)上单调递减,
而y=log3t在定义域上单调递增,
由复合函数的单调性可知,y=log3(x2-2x)在(-∞,0)上单调递减.故选C.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.若函数f (x)=loga在区间内恒有f (x)>0,则f (x)的单调递增区间为( )
A.(0,+∞) B.(2,+∞)
C.(1,+∞) D.
13
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [令M=x2+x,故x∈时,M∈(1,+∞),恒有f (x)>0,所以a>1,所以函数y=logaM为增函数,又M=-,所以M的单调递增区间为.又x2+x>0,所以x>0或x<-,所以函数f (x)的单调递增区间为(0,+∞).故选A.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
二、多项选择题
7.(2025·河南郑州模拟)关于函数f (x)=log3,下列结论正确的是( )
A.定义域为(-∞,-1)∪(3,+∞)
B.f (x)是偶函数
C.f (x)的图象关于点(1,0)对称
D.f (x)在(3,+∞)上单调递增
13
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
ACD [对于A,由>0得x<-1或x>3,故定义域为(-∞,-1) ∪(3,+∞),A正确;
对于B,因为定义域不关于原点对称,故f (x)不是偶函数,B错误;
对于C,因为f (1-x)+f (1+x)=log3+log3
=log3+log3=log3=log31=0,
所以f (x)的图象关于点(1,0)对称,C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
对于D,f (x)=log3=log3,
因为函数t=1-在区间(3,+∞)上单调递增,且y=log3t在(0,
+∞)上单调递增,
所以f (x)在(3,+∞)上单调递增,D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2025·湖北重点高中联考)已知实数x,y,z满足2x=3,3y=4,4z=5,则下列结论正确的是( )
A.y< B.xyz>2
C.y
13
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [因为2x=3,3y=4,4z=5,
所以x=log23,y=log34,z=log45,
对于A,因为43<34,则log343
对于B,xyz=log23·log34·log45=log25>log24=2,故B正确;
对于C,y-z=log34-log45==,
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
因为0
又(lg 4)2==>,
所以(lg 4)2-lg 3lg 5>0,即y-z>0,所以y>z,故C错误;
对于D,因为x=log23>1,y=log34>1,
所以x+y=log23+log34>2=2=2,故D正确.故选ABD.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
三、填空题
9.(2024·河南郑州三模)已知logab+4logba=4,则的值为________.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[因为logab+4logba=4,
所以logab+=4,可得 (logab)2-4logab+4=0,
即(logab-2)2=0,所以logab=2,即a2=b,
所以==.]
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·安徽宣城模拟)已知实数x满足不等式2(log2x)2-5log2x+2≤0,则函数f (x)=log2·log2的最大值是________.
13
[由2(log2x)2-5log2x+2≤0,
解得≤log2x≤2,
f (x)=log2·log2=(log2x-1)(log2x-2)=-,
当log2x=时,f (x)取得最大值.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
四、解答题
11.已知f (x)=.
(1)若a=2,求f (x)的值域;
(2)若f (x)在(1,+∞)上单调递减,求a的取值范围.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)当a=2时,f (x)=,
令t=x2-2x+10=(x-1)2+9,
=-2,
∴f (x)的值域为(-∞,-2].
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)令u=x2-ax+5a,
∵y=为减函数,f (x)在(1,+∞)上单调递减,
∴u=x2-ax+5a在(1,+∞)上单调递增,
∴解得-≤a≤2,
∴a的取值范围是.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·江苏盐城模拟)已知函数f (x)=log4.
(1)解关于x的不等式f (x)>3;
(2)若存在x∈[2,4],使得不等式f (2x)-a·log2x+1≥0成立,求实数a的取值范围.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为f (x)的定义域为(0,+∞),则
f (x)=log2·2log2=(log2x-2)(log2x-4)=(log2x)2-6log2x+8,
设log2x=t(t∈R),则不等式可化为t2-6t+8>3,
即t2-6t+5>0,
解得t<1或t>5,即log2x<1或log2x>5,
解得0
所以不等式的解集为{x|0
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为f (2x)-a·log2x+1≥0,
所以(log2x-1)·(log2x-3)-alog2x+1≥0,
设log2x=t,则t∈[1,2],
原问题化为:存在t∈[1,2],t2-4t+4-at≥0.
即a≤t+-4在t∈[1,2]上有解.
因为y=t+-4在[1,2]上单调递减,
所以=1,所以a≤1.
即实数a的取值范围是(-∞,1].
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
13.已知函数f (x)=2lg (10x+a)-x,a∈R.
(1)当a=1时,判断函数f (x)的奇偶性并证明;
(2)给定实数a>0且a≠1,问是否存在直线x=x0,使得函数f (x)的图象关于直线x=x0对称?若存在,求出x0的值(用a表示);若不存在,请说明理由.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)当a=1时,f (x)=2lg (10x+1)-x,
函数f (x)为偶函数,证明如下:
∵f (-x)=2lg (10-x+1)-(-x)=2lg +x=2lg (1+10x)-
2lg (10x)+x=2lg (10x+1)-x=f (x),
又函数的定义域为R,∴函数f (x)为偶函数.
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)假设存在直线x=x0,使得函数f (x)的图象关于直线x=x0对称,则
f (x0+x)=f (x0-x),
∴2lg (+a)-(x0+x)=2lg (+a)-(x0-x),
即lg (+a)-lg (+a)=x,
即lg =x,∴=10x,
即+a=10x(+a)=+a·10x,
13
题号
1
3
5
2
4
6
8
7
9
10
11
12
)=0,
=0,即a=,
∵a>0且a≠1,
∴x0=lg a,
故存在x0=lg a,使得函数f (x)的图象关于直线x=x0对称.
13
谢 谢!
同课章节目录
