《高考快车道》2026版高三一轮总复习(数学)28 第三章 思维进阶课4 极值点偏移问题
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习(数学)28 第三章 思维进阶课4 极值点偏移问题 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 11:49:17 | ||
图片预览










文档简介
(共35张PPT)
第三章
一元函数的导数及其应用
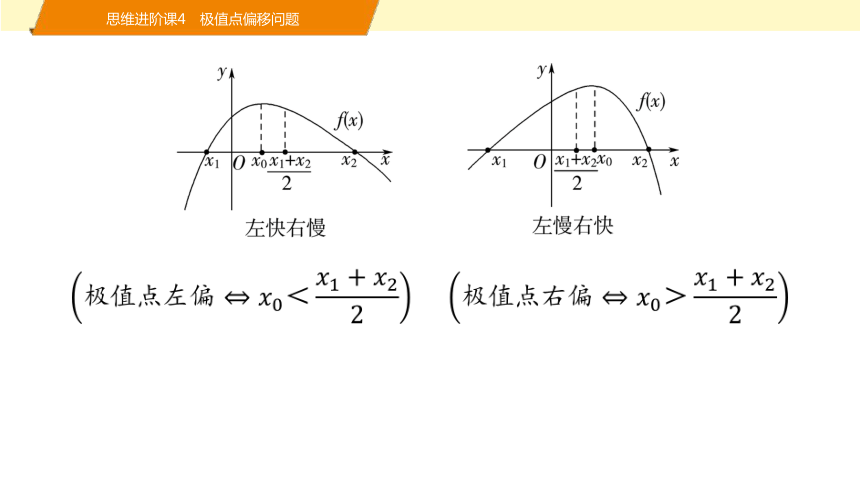
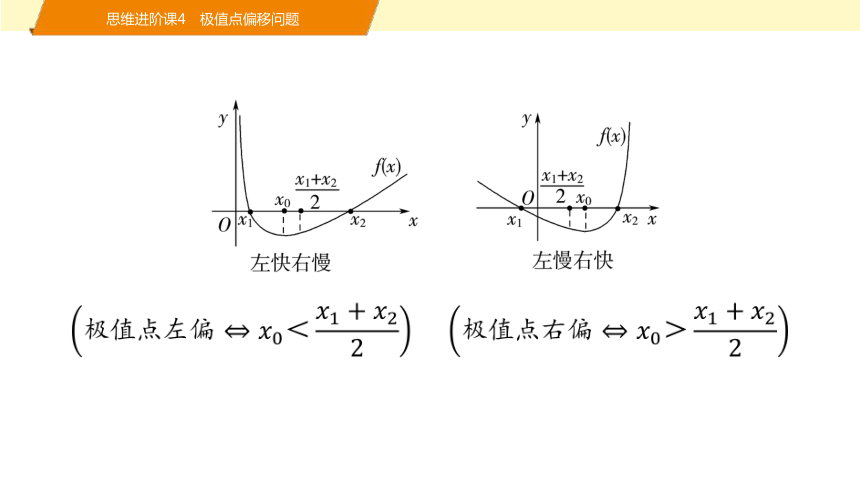
思维进阶课4 极值点偏移问题
极值点偏移的判定定理
对于可导函数y=f (x)在区间(a,b)上只有一个极大(小)值点x0,方程f (x)=0的解分别为x1,x2,且a<x1<x2<b.
(1)若0=f (x1)<f (2x0-x2),则<(>)x0,即函数y=f (x)在区间(x1,x2)上的极大(小)值点x0右(左)偏;
(2)若0=f (x1)>f (2x0-x2),则>(<)x0,即函数y=f (x)在区间(x1,x2)上的极大(小)值点x0左(右)偏.
【思维突破妙招】 证明极值点偏移的相关问题,一般有以下几种方法:
(1)证明x1+x2<2a(或x1+x2>2a):
①构造函数g(x)=f (x)-f (2a-x),求导,确定函数y=f (x)和函数y=g(x)的单调性;
②确定x1,x2满足x1<a<x2,且f (x1)=f (x2),由函数值g(x1)与g(a)的大小关系,得g(x1)=f (x1)-f (2a-x1)=f (x2)-f (2a-x1)与零的大小关系;
③由函数y=f (x)在区间(a,+∞)上的单调性得到x2与2a-x1的大小关系,从而证明相应问题.
(2)证明x1x2<a2(或x1x2>a2)(x1,x2都为正数):
①构造函数g(x)=f (x)-f ,求导,确定函数y=f (x)和函数y=g(x)的单调性;
②确定x1,x2满足x1<a<x2,且f (x1)=f (x2),由函数值g(x1)与g(a)的大小关系,得g(x1)=f (x1)-f =f (x2)-f 与零的大小关系;
③由函数y=f (x)在区间(a,+∞)上的单调性得到x2与的大小关系,从而证明相应问题.
(3)应用对数平均不等式<<证明极值点偏移:
①由题中等式产生对数;
②将所得含对数的等式进行变形得到;
③利用对数平均不等式来证明相应的问题.
技法 对称化构造辅助函数
[典例] 已知函数f (x)=xe-x.
(1)求函数f (x)的单调区间和极值;
(2)若x1≠x2且f (x1)=f (x2),求证:x1+x2>2.
[解] (1)f ′(x)=e-x(1-x),x∈R.
令f ′(x)>0,得x<1;令f ′(x)<0,得x>1,
所以函数f (x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,
所以f (x)有极大值f (1)=,无极小值.
(2)法一(对称化构造):
由(1)知,不妨设02,
只要证x2>2-x1>1.
由于f (x)在(1,+∞)上单调递减,故只要证f (x2)令H(x)=f (x)-f (2-x)=xe-x-(2-x)ex-2(00,2-x>x,
所以e2-x>ex,即e2-x-ex>0,所以H′(x)>0,所以H(x)在(0,1)上单调递增,所以H(x)2.
法二(比值代换):设0令t=>1,则x2=tx1,代入上式得ln x1-x1=ln t+ln x1-tx1,得x1=,x2=,所以即证x1+x2=>2,即ln t->0,
设g(t)=ln t-(t>1),所以g′(t)==>0,
所以当t>1时,g(t)单调递增,所以g(t)>g(1)=0,所以ln t->0,
故x1+x2>2.
名师点评 极值点偏移问题的常用策略
首先进行变量的转化,即由已知条件入手,寻找双变量所满足的关系式,或者通过比值代换,利用关系式将其中一个变量用另一个变量表示,代入要证明的不等式,化简后根据其结构特点构造函数,再借助导数,判断函数的单调性,从而求其最值,并把最值应用到所证不等式.
[跟进训练]
1.(2022·全国甲卷节选)已知函数f (x)=-ln x+x-a.证明:若f (x)有两个零点x1,x2,则x1x2<1.
[证明] 法一(对称化构造):由题意知f (x)的定义域为(0,+∞),
f ′(x)=,可得函数f (x)在(0,1)上单调递减,在(1,+∞)上单调递增.
由题知, f (x)的一个零点小于1,一个零点大于1,
不妨设0<x1<1<x2,
要证x1x2<1,即证x1<,
因为x1,∈(0,1),即证f (x1)>f ,
因为f (x1)=f (x2),即证f (x2)>f ,
即证-ln x+x-x-ln x->0,x∈(1,+∞),
即证-x-2>0,
下面证明当x>1时,-x>0,ln x-<0.
设g(x)=-x,x>1,
则g′(x)=ex-
=ex-
==,
设φ(x)=(x>1),φ′(x)=ex=ex>0,
所以φ(x)>φ(1)=e,而<e,
所以->0,所以g′(x)>0,
所以g(x)在(1,+∞)上单调递增,
即g(x)>g(1)=0,所以-x>0.
令h(x)=ln x-,x>1,
h′(x)===<0,
所以h(x)在(1,+∞)上单调递减,
即h(x)<h(1)=0,所以ln x-<0.
综上,-x-2>0,所以x1x2<1.
法二(对数平均不等式):f (x)=-ln x+x-a=ex-ln x+x-ln x-a,
令t=x-ln x,则g(t)=et+t-a,易知g(t)单调递增,
所以g(t)有且仅有一个零点t0,
又f (x)有两个零点x1,x2,
所以x-ln x=t0有两个实根x1和x2,
所以
由对数平均不等式得<=1<,所以x1x2<1.
2.已知函数f (x)=ln x-ax2,若x1,x2是方程f (x)=0的两个不等实根,求证:>2e.
[证明] 因为x1,x2是方程ln x-ax2=0的两个不等实根,
ln x-ax2=0 2ln x-2ax2=0,
即x1,x2是方程ln x2-2ax2=0的两个不等实根,
令t=x2(t>0),则t1=,t2=,
即t1,t2是方程2a=的两个不等实根.
令g(t)=,则g′(t)=,
当0<t<e时,g′(t)>0,当t>e时,g′(t)<0,
所以g(t)在(0,e)上单调递增,在(e,+∞)上单调递减,g(e)=,
当t→0时,g(t)→-∞;
当t→+∞时,g(t)>0且g(t)→0.
所以0<2a<,即0<a<.
令1<t1<e<t2,要证>2e,只需证t1+t2>2e.
法一(对称化构造):令h(t)=g(t)-g(2e-t),t∈(1,e),
则h(t)=g(t)-g(2e-t)==,
令φ(t)=(2e-t)ln t-t ln (2e-t),
则φ′(t)=-1-ln t-ln (2e-t)+=-ln (-t2+2et)>-2>0,
所以φ(t)在(1,e)上单调递增,φ(t)<φ(e)=0,
所以h(t)=g(t)-g(2e-t)<0,所以g(t)<g(2e-t),
所以g(t2)=g(t1)<g(2e-t1),所以t2>2e-t1,
即t1+t2>2e,所以>2e.
法二(对数平均不等式):
先证<,令0<x1<x2,
只需证<,
只需证-ln x<0,
令φ(x)=-ln x(x>1),φ′(x)==<0,
所以φ(x)在(1,+∞)上单调递减,所以φ(x)<φ(1)=0.即<得证.
因为=,所以=<,
所以ln t1+ln t2>2,即t1t2>e2,
所以t1+t2>2>2e.
即>2e.
题号
1
3
2
4
进阶特训(四) 极值点偏移问题
1.(2024·广东湛江一模)已知函数f (x)=.
(1)讨论f (x)的单调性;
(2)若方程f (x)=1有两个根x1,x2,求实数a的取值范围,并证明:x1x2>1.
[解] (1)由题意可得x>0,>0,所以a>0,
f (x)==的定义域为(0,+∞),
又f ′(x)==-,
由f ′(x)=0,得x=1,
当00,则f (x)在(0,1)上单调递增,
当x>1时,f ′(x)<0,则f (x)在(1,+∞)上单调递减.
题号
1
3
2
4
(2)由=1,得=a,设g(x)=,
g′(x)==,由g′(x)=0,得x=1,
当00,则g(x)在(0,1)上单调递增,
当x>1时,g′(x)<0,则g(x)在(1,+∞)上单调递减,
又g=0,g(1)=1,且当x趋近于正无穷时,g(x)趋近于0,
g(x)=的图象如图,
所以当0题号
1
3
2
4
证明:不妨设x1设h(x)=g(x)-g=-x(1-ln x),h′(x)=+ln x=ln x≥0,所以h(x)在(0,+∞)上单调递增,
又h(1)=0,所以h(x1)=g(x1)-g<0,即g(x1)1,>1,g(x)在(1,+∞)上单调递减,所以x2>,故x1x2>1.
题号
1
3
2
4
2.已知函数f (x)=ex-x2.
(1)求证:f (x)在R上为增函数;
(2)若f (x1)+f (x2)=e,x1题号
1
3
2
4
[证明] (1)由题意知f ′(x)=ex-ex,令g(x)=ex-ex,则g′(x)=ex-e.
令g′(x)=0,得x=1,当x∈(-∞,1)时,g′(x)<0,g(x)单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,所以g(x)min=g(1)=0,故f ′(x)≥0,故f (x)在R上为增函数.
(2)由(1)知f (x)为增函数,且f (1)=,
故由f (x1)+f (x2)=2f (1),x1可得f (x1)欲证x1+x2<2,只需证x1<2-x2,
即证f (x1)即证e-f (x2)令F (x)=f (x)+f (2-x)-e(x>1),
则F ′(x)=f ′(x)-f ′(2-x)=ex-ex-e2-x+e(2-x),
题号
1
3
2
4
令H(x)=F ′(x),则H′(x)=ex-e+e2-x-e=ex+e2-x-2e>2-2e=0,
故F ′(x)为增函数,F ′(x)>F ′(1)=0,
故F (x)为增函数,F (x)>F (1)=0,
故F (x2)>0,则e-f (x2)所以x1+x2<2.
题号
1
3
2
4
3.已知函数f (x)=x ln x-mx2-x,m∈R有两个极值点x1,x2,求证:x1x2>e2.
题号
1
3
2
4
[证明] 要证x1x2>e2,只需证ln x1+ln x2>2,
若f (x)有两个极值点x1,x2,
即f ′(x)有两个变号零点,
又f ′(x)=ln x-mx,
所以x1,x2是方程f ′(x)=0的两个不同的实根,
即 解得m=.
另一方面,由
得ln x2-ln x1=m(x2-x1),
从而可得=,
于是ln x1+ln x2==.
不妨设01.
因此ln x1+ln x2=,t>1.
题号
1
3
2
4
要证ln x1+ln x2>2,即证>2,t>1,
即当t>1时,有ln t>,
设函数h(t)=ln t-,t>1,
则h′(t)==>0,
所以h(t)在(1,+∞)上单调递增.
又h(1)=0,因此h(t)>h(1)=0.
于是当t>1时,有ln t>,
所以ln x1+ln x2>2成立,即x1x2>e2得证.
题号
1
3
2
4
4.(2024·河北保定二模)已知函数f (x)=ax-x ln x,f ′(x)为其导函数.
(1)若f (x)≤1恒成立,求a的取值范围;
(2)若存在两个不同的正数x1,x2,使得f (x1)=f (x2),证明:
f ′()>0.
题号
1
3
2
4
[解] (1)f ′(x)=a-1-ln x,当00,f (x)单调递增;
当x>ea-1时,f ′(x)<0,f (x)单调递减.
所以f (x)max=f (ea-1)=ea-1≤1,
解得a≤1,即a的取值范围为(-∞,1].
(2)证明:不妨设x10,
即证所以只需证f (x1)令g(x)=f (x)-f ,x∈(ea-1,ea),
则g(ea-1)=0,g′(x)=.
当x>ea-1时,a-1-ln x<0,x2-e2a-2>0,
题号
1
3
2
4
则g′(x)<0,
所以g(x)在(ea-1,ea)上单调递减,
则g(x)由(1)知f (x)在(0,ea-1)上单调递增,所以x1<,
从而f ′()>0成立.
题号
1
3
2
4
谢 谢!
第三章
一元函数的导数及其应用
思维进阶课4 极值点偏移问题
极值点偏移的判定定理
对于可导函数y=f (x)在区间(a,b)上只有一个极大(小)值点x0,方程f (x)=0的解分别为x1,x2,且a<x1<x2<b.
(1)若0=f (x1)<f (2x0-x2),则<(>)x0,即函数y=f (x)在区间(x1,x2)上的极大(小)值点x0右(左)偏;
(2)若0=f (x1)>f (2x0-x2),则>(<)x0,即函数y=f (x)在区间(x1,x2)上的极大(小)值点x0左(右)偏.
【思维突破妙招】 证明极值点偏移的相关问题,一般有以下几种方法:
(1)证明x1+x2<2a(或x1+x2>2a):
①构造函数g(x)=f (x)-f (2a-x),求导,确定函数y=f (x)和函数y=g(x)的单调性;
②确定x1,x2满足x1<a<x2,且f (x1)=f (x2),由函数值g(x1)与g(a)的大小关系,得g(x1)=f (x1)-f (2a-x1)=f (x2)-f (2a-x1)与零的大小关系;
③由函数y=f (x)在区间(a,+∞)上的单调性得到x2与2a-x1的大小关系,从而证明相应问题.
(2)证明x1x2<a2(或x1x2>a2)(x1,x2都为正数):
①构造函数g(x)=f (x)-f ,求导,确定函数y=f (x)和函数y=g(x)的单调性;
②确定x1,x2满足x1<a<x2,且f (x1)=f (x2),由函数值g(x1)与g(a)的大小关系,得g(x1)=f (x1)-f =f (x2)-f 与零的大小关系;
③由函数y=f (x)在区间(a,+∞)上的单调性得到x2与的大小关系,从而证明相应问题.
(3)应用对数平均不等式<<证明极值点偏移:
①由题中等式产生对数;
②将所得含对数的等式进行变形得到;
③利用对数平均不等式来证明相应的问题.
技法 对称化构造辅助函数
[典例] 已知函数f (x)=xe-x.
(1)求函数f (x)的单调区间和极值;
(2)若x1≠x2且f (x1)=f (x2),求证:x1+x2>2.
[解] (1)f ′(x)=e-x(1-x),x∈R.
令f ′(x)>0,得x<1;令f ′(x)<0,得x>1,
所以函数f (x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,
所以f (x)有极大值f (1)=,无极小值.
(2)法一(对称化构造):
由(1)知,不妨设0
只要证x2>2-x1>1.
由于f (x)在(1,+∞)上单调递减,故只要证f (x2)
所以e2-x>ex,即e2-x-ex>0,所以H′(x)>0,所以H(x)在(0,1)上单调递增,所以H(x)
法二(比值代换):设0
设g(t)=ln t-(t>1),所以g′(t)==>0,
所以当t>1时,g(t)单调递增,所以g(t)>g(1)=0,所以ln t->0,
故x1+x2>2.
名师点评 极值点偏移问题的常用策略
首先进行变量的转化,即由已知条件入手,寻找双变量所满足的关系式,或者通过比值代换,利用关系式将其中一个变量用另一个变量表示,代入要证明的不等式,化简后根据其结构特点构造函数,再借助导数,判断函数的单调性,从而求其最值,并把最值应用到所证不等式.
[跟进训练]
1.(2022·全国甲卷节选)已知函数f (x)=-ln x+x-a.证明:若f (x)有两个零点x1,x2,则x1x2<1.
[证明] 法一(对称化构造):由题意知f (x)的定义域为(0,+∞),
f ′(x)=,可得函数f (x)在(0,1)上单调递减,在(1,+∞)上单调递增.
由题知, f (x)的一个零点小于1,一个零点大于1,
不妨设0<x1<1<x2,
要证x1x2<1,即证x1<,
因为x1,∈(0,1),即证f (x1)>f ,
因为f (x1)=f (x2),即证f (x2)>f ,
即证-ln x+x-x-ln x->0,x∈(1,+∞),
即证-x-2>0,
下面证明当x>1时,-x>0,ln x-<0.
设g(x)=-x,x>1,
则g′(x)=ex-
=ex-
==,
设φ(x)=(x>1),φ′(x)=ex=ex>0,
所以φ(x)>φ(1)=e,而<e,
所以->0,所以g′(x)>0,
所以g(x)在(1,+∞)上单调递增,
即g(x)>g(1)=0,所以-x>0.
令h(x)=ln x-,x>1,
h′(x)===<0,
所以h(x)在(1,+∞)上单调递减,
即h(x)<h(1)=0,所以ln x-<0.
综上,-x-2>0,所以x1x2<1.
法二(对数平均不等式):f (x)=-ln x+x-a=ex-ln x+x-ln x-a,
令t=x-ln x,则g(t)=et+t-a,易知g(t)单调递增,
所以g(t)有且仅有一个零点t0,
又f (x)有两个零点x1,x2,
所以x-ln x=t0有两个实根x1和x2,
所以
由对数平均不等式得<=1<,所以x1x2<1.
2.已知函数f (x)=ln x-ax2,若x1,x2是方程f (x)=0的两个不等实根,求证:>2e.
[证明] 因为x1,x2是方程ln x-ax2=0的两个不等实根,
ln x-ax2=0 2ln x-2ax2=0,
即x1,x2是方程ln x2-2ax2=0的两个不等实根,
令t=x2(t>0),则t1=,t2=,
即t1,t2是方程2a=的两个不等实根.
令g(t)=,则g′(t)=,
当0<t<e时,g′(t)>0,当t>e时,g′(t)<0,
所以g(t)在(0,e)上单调递增,在(e,+∞)上单调递减,g(e)=,
当t→0时,g(t)→-∞;
当t→+∞时,g(t)>0且g(t)→0.
所以0<2a<,即0<a<.
令1<t1<e<t2,要证>2e,只需证t1+t2>2e.
法一(对称化构造):令h(t)=g(t)-g(2e-t),t∈(1,e),
则h(t)=g(t)-g(2e-t)==,
令φ(t)=(2e-t)ln t-t ln (2e-t),
则φ′(t)=-1-ln t-ln (2e-t)+=-ln (-t2+2et)>-2>0,
所以φ(t)在(1,e)上单调递增,φ(t)<φ(e)=0,
所以h(t)=g(t)-g(2e-t)<0,所以g(t)<g(2e-t),
所以g(t2)=g(t1)<g(2e-t1),所以t2>2e-t1,
即t1+t2>2e,所以>2e.
法二(对数平均不等式):
先证<,令0<x1<x2,
只需证<,
只需证-ln x<0,
令φ(x)=-ln x(x>1),φ′(x)==<0,
所以φ(x)在(1,+∞)上单调递减,所以φ(x)<φ(1)=0.即<得证.
因为=,所以=<,
所以ln t1+ln t2>2,即t1t2>e2,
所以t1+t2>2>2e.
即>2e.
题号
1
3
2
4
进阶特训(四) 极值点偏移问题
1.(2024·广东湛江一模)已知函数f (x)=.
(1)讨论f (x)的单调性;
(2)若方程f (x)=1有两个根x1,x2,求实数a的取值范围,并证明:x1x2>1.
[解] (1)由题意可得x>0,>0,所以a>0,
f (x)==的定义域为(0,+∞),
又f ′(x)==-,
由f ′(x)=0,得x=1,
当0
当x>1时,f ′(x)<0,则f (x)在(1,+∞)上单调递减.
题号
1
3
2
4
(2)由=1,得=a,设g(x)=,
g′(x)==,由g′(x)=0,得x=1,
当0
当x>1时,g′(x)<0,则g(x)在(1,+∞)上单调递减,
又g=0,g(1)=1,且当x趋近于正无穷时,g(x)趋近于0,
g(x)=的图象如图,
所以当0
1
3
2
4
证明:不妨设x1
又h(1)=0,所以h(x1)=g(x1)-g<0,即g(x1)
题号
1
3
2
4
2.已知函数f (x)=ex-x2.
(1)求证:f (x)在R上为增函数;
(2)若f (x1)+f (x2)=e,x1
1
3
2
4
[证明] (1)由题意知f ′(x)=ex-ex,令g(x)=ex-ex,则g′(x)=ex-e.
令g′(x)=0,得x=1,当x∈(-∞,1)时,g′(x)<0,g(x)单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,所以g(x)min=g(1)=0,故f ′(x)≥0,故f (x)在R上为增函数.
(2)由(1)知f (x)为增函数,且f (1)=,
故由f (x1)+f (x2)=2f (1),x1
即证f (x1)
则F ′(x)=f ′(x)-f ′(2-x)=ex-ex-e2-x+e(2-x),
题号
1
3
2
4
令H(x)=F ′(x),则H′(x)=ex-e+e2-x-e=ex+e2-x-2e>2-2e=0,
故F ′(x)为增函数,F ′(x)>F ′(1)=0,
故F (x)为增函数,F (x)>F (1)=0,
故F (x2)>0,则e-f (x2)
题号
1
3
2
4
3.已知函数f (x)=x ln x-mx2-x,m∈R有两个极值点x1,x2,求证:x1x2>e2.
题号
1
3
2
4
[证明] 要证x1x2>e2,只需证ln x1+ln x2>2,
若f (x)有两个极值点x1,x2,
即f ′(x)有两个变号零点,
又f ′(x)=ln x-mx,
所以x1,x2是方程f ′(x)=0的两个不同的实根,
即 解得m=.
另一方面,由
得ln x2-ln x1=m(x2-x1),
从而可得=,
于是ln x1+ln x2==.
不妨设0
因此ln x1+ln x2=,t>1.
题号
1
3
2
4
要证ln x1+ln x2>2,即证>2,t>1,
即当t>1时,有ln t>,
设函数h(t)=ln t-,t>1,
则h′(t)==>0,
所以h(t)在(1,+∞)上单调递增.
又h(1)=0,因此h(t)>h(1)=0.
于是当t>1时,有ln t>,
所以ln x1+ln x2>2成立,即x1x2>e2得证.
题号
1
3
2
4
4.(2024·河北保定二模)已知函数f (x)=ax-x ln x,f ′(x)为其导函数.
(1)若f (x)≤1恒成立,求a的取值范围;
(2)若存在两个不同的正数x1,x2,使得f (x1)=f (x2),证明:
f ′()>0.
题号
1
3
2
4
[解] (1)f ′(x)=a-1-ln x,当0
当x>ea-1时,f ′(x)<0,f (x)单调递减.
所以f (x)max=f (ea-1)=ea-1≤1,
解得a≤1,即a的取值范围为(-∞,1].
(2)证明:不妨设x1
即证
则g(ea-1)=0,g′(x)=.
当x>ea-1时,a-1-ln x<0,x2-e2a-2>0,
题号
1
3
2
4
则g′(x)<0,
所以g(x)在(ea-1,ea)上单调递减,
则g(x)
从而f ′()>0成立.
题号
1
3
2
4
谢 谢!
同课章节目录
