第三章 指数运算与指数函数(预习衔接.夯实基础.含解析)2025-2026学年高一上学期数学必修第一册北师大版(2019)
文档属性
| 名称 | 第三章 指数运算与指数函数(预习衔接.夯实基础.含解析)2025-2026学年高一上学期数学必修第一册北师大版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 09:59:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 指数运算与指数函数
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
2.(2024秋 朝阳区校级期中)随着我国经济的不断发展,2023年年底某地区农民人均年收入为7000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2030年年底该地区的农民人均年收入为( )
A.7000×1.06×7元 B.7000×1.067元
C.7000×1.06×8元 D.7000×1.068元
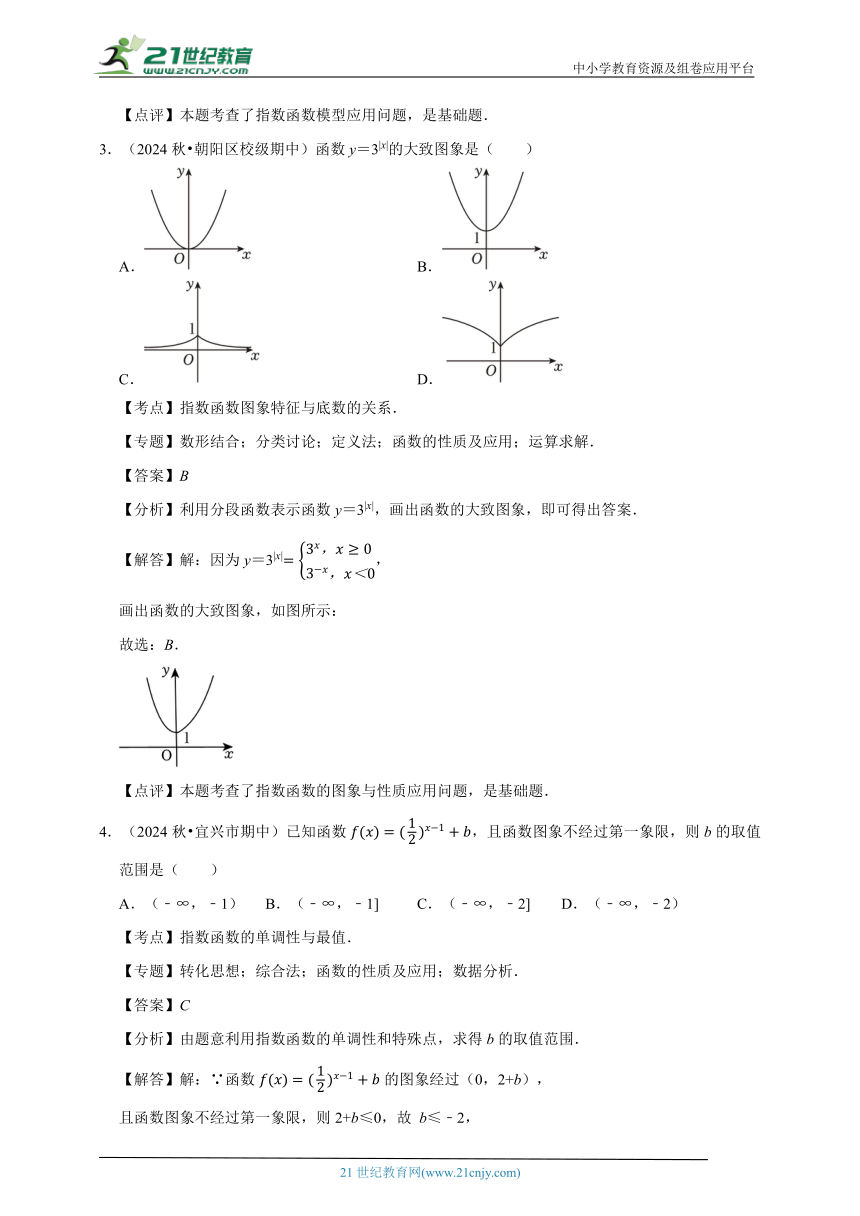
3.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
4.(2024秋 宜兴市期中)已知函数,且函数图象不经过第一象限,则b的取值范围是( )
A.(﹣∞,﹣1) B.(﹣∞,﹣1] C.(﹣∞,﹣2] D.(﹣∞,﹣2)
二.多选题(共3小题)
(多选)5.(2024秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
(多选)6.(2024秋 广州期中)已知实数a满足a+a﹣1=4,下列选项中正确的是( )
A.a2+a﹣2=14 B.a﹣a﹣1=2
C. D.
(多选)7.(2024秋 芒市校级期中)下列各式正确的有( )
A. B.
C. D.
三.填空题(共4小题)
8.(2024秋 新吴区校级期中)若,则a2+a﹣2= .
9.(2024秋 朝阳区校级期中)计算: .
10.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= .
11.(2024秋 中山市期中)求值: .
四.解答题(共4小题)
12.(2024秋 西湖区校级期中)求下列各式的值:
(1)log78 (0.2)1﹣log53+2π0 ()﹣6;
(2)已知x﹣1+x=7(x>0),求.
13.(2024秋 浦东新区校级期中)已知函数f(x)=ax(其中a>0,且a≠1).
(1)若f(b)+f(﹣b)=3,求f(2b)+f(﹣2b)的值.
(2)求关于x的方程f(2x)﹣2f(x)+1=0的解.
14.(2024秋 张家口期中)近几年3D打印手办深受青少年的喜爱,某工厂计划在2024年利用新技术生产手办,通过调查分析.生产手办全年需投入固定成本12万元,生产x(千件)手办,需另投入成本C(x)(万元).且,由市场调研知每件手办售价90元,且每年内生产的手办当年能全部销售完.
(1)求出2024年的利润L(x)(万元)关于年产量x(千件)的表达式;
(2)2024年年产量为多少(千件)时,该工厂所获利润最大?最大利润是多少?
15.(2024秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
预习衔接.夯实基础 指数运算与指数函数
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
【考点】指数函数的单调性与最值;对数函数的单调性与最值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】利用指数函数与对数函数的性质分析判断即可.
【解答】解:∵y=3x为R上的增函数,﹣2.5<﹣2.3,
∴0<a3﹣2.5<c=3﹣2.3<1,
又b0,
∴b<a<c.
故选:C.
【点评】本题考查指数函数与对数函数的性质,属于基础题.
2.(2024秋 朝阳区校级期中)随着我国经济的不断发展,2023年年底某地区农民人均年收入为7000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2030年年底该地区的农民人均年收入为( )
A.7000×1.06×7元 B.7000×1.067元
C.7000×1.06×8元 D.7000×1.068元
【考点】指数函数的实际应用.
【专题】应用题;函数思想;数学模型法;函数的性质及应用;数学建模.
【答案】B
【分析】根据指数增长模型计算即可.
【解答】解:设经过x年,该地区的农民人均年收入为y元,
根据题意得,y=7000×1.06x,
从2023年年底到2030年年底共经过了7年,
所以2030年年底该地区的农民人均年收入为7000×1.067元.
故选:B.
【点评】本题考查了指数函数模型应用问题,是基础题.
3.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
【考点】指数函数图象特征与底数的关系.
【专题】数形结合;分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】利用分段函数表示函数y=3|x|,画出函数的大致图象,即可得出答案.
【解答】解:因为y=3|x|,
画出函数的大致图象,如图所示:
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
4.(2024秋 宜兴市期中)已知函数,且函数图象不经过第一象限,则b的取值范围是( )
A.(﹣∞,﹣1) B.(﹣∞,﹣1] C.(﹣∞,﹣2] D.(﹣∞,﹣2)
【考点】指数函数的单调性与最值.
【专题】转化思想;综合法;函数的性质及应用;数据分析.
【答案】C
【分析】由题意利用指数函数的单调性和特殊点,求得b的取值范围.
【解答】解:∵函数的图象经过(0,2+b),
且函数图象不经过第一象限,则2+b≤0,故 b≤﹣2,
故选:C.
【点评】本题主要考查指数函数的单调性和特殊点,属于基础题.
二.多选题(共3小题)
(多选)5.(2024秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
【考点】指数函数图象特征与底数的关系;定义法求解函数的单调性.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】根据题意,结合指数函数、对数函数,以及函数的单调性和反函数的关系,逐项判定,即可求解.
【解答】解:对于A中,函数f(x)=loga(x+1)+loga(x﹣1),则满足,
解得x>1,
即f(x)的定义域为(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,故A不正确;
对于B中,函数f(x)=2ax﹣2﹣1(a>0且a≠1),
令x﹣2=0,可得x=2,
则f(2)=2a0﹣1=1,
所以f(x)恒过定点(2,1),所以B正确;
对于C中,函数,
因为函数y=ex+1为单调递增函数,且y>0
所以为递减函数,则为递增函数,所以C正确;
对于D中,由函数与函数互为反函数,
所以函数与函数y=﹣log2x的图像关于直线y=x对称,所以D正确.
故选:BCD.
【点评】本题主要考查了函数的单调性和奇偶性,考查了反函数的定义,属于基础题.
(多选)6.(2024秋 广州期中)已知实数a满足a+a﹣1=4,下列选项中正确的是( )
A.a2+a﹣2=14 B.a﹣a﹣1=2
C. D.
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】ACD
【分析】根据a2+a﹣2=(a+a﹣1)2﹣2a a﹣1即可判断A;
根据(a﹣a﹣1)2=a2+a﹣2﹣2a a﹣1即可判断B,注意符号;
根据即可判断C;
利用立方和公式即可判断D.
【解答】解:因为a+a﹣1=4,所以a>0,a2+a﹣2=(a+a﹣1)2﹣2a a﹣1=16﹣2=14,故A正确;
(a﹣a﹣1)2=a2+a﹣2﹣2a a﹣1=12,所以,故B错误;
,
又a>0,所以,则,故C正确;,故D正确.
故选:ACD.
【点评】本题考查了完全平方公式和立方和公式,是基础题.
(多选)7.(2024秋 芒市校级期中)下列各式正确的有( )
A. B.
C. D.
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】运用根式的化简方法直接求解即可.
【解答】解:∵∴A项错误;
∵,
∴B项正确;
∵,∴C项正确;
∵,∴D项正确.
故选:BCD.
【点评】本题主要考查了根式的化简,属于基础题.
三.填空题(共4小题)
8.(2024秋 新吴区校级期中)若,则a2+a﹣2= 47 .
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】47.
【分析】结合指数幂的运算性质即可求解.
【解答】解:若,
则a+a﹣1+2=9,即a+a﹣1=7,
则a2+a﹣2+2=49,即a2+a﹣2=47.
故答案为:47.
【点评】本题主要考查了指数幂的运算性质,属于基础题.
9.(2024秋 朝阳区校级期中)计算: ﹣19681 .
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】﹣19681.
【分析】根据对数的运算性质和指数幂的运算性质求解.
【解答】解:原式=log39+(﹣27)3(﹣19683)=2+(﹣19683)=﹣19681.
故答案为:﹣19681.
【点评】本题主要考查了对数的运算性质,考查了指数幂的运算性质,属于基础题.
10.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= ﹣5 .
【考点】指数函数的单调性与最值.
【专题】转化思想;定义法;不等式的解法及应用;运算求解.
【答案】﹣5.
【分析】根据y=2x在R上单调递增,判断大小列不等式进行解答即可.
【解答】解:不等式可化为23﹣3x,
因为y=2x在R上单调递增,
所以x2﹣2x﹣3<3﹣3x,整理得x2+x﹣6<0,
由题意知两不等式的解集相同,则a=1,b=﹣6,
所以a+b=﹣5.
故答案为:﹣5.
【点评】本题考查了函数与不等式的应用问题,是基础题.
11.(2024秋 中山市期中)求值: .
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】.
【分析】根据根式、分数指数幂运算、零指数幂运算得出结果.
【解答】解: .
故答案为:.
【点评】本题主要考查了有理数指数幂的运算性质,属于基础题.
四.解答题(共4小题)
12.(2024秋 西湖区校级期中)求下列各式的值:
(1)log78 (0.2)1﹣log53+2π0 ()﹣6;
(2)已知x﹣1+x=7(x>0),求.
【考点】有理数指数幂及根式化简运算求值.
【专题】综合法;函数的性质及应用;能力层次;运算求解.
【答案】(1);
(2)18.
【分析】(1)结合指数及对数的运算性质进行化简即可求解;
(2)结合指数幂的运算性质即可求解.
【解答】解:(1)log78 (0.2)1﹣log53+2π0 ()﹣6
=﹣162
=﹣1616
;
(2)因为x﹣1+x=7,x>0,
则(x)2=x+x﹣1+2=9,
则x3,
()3+(x)3=(x)(x+x﹣1﹣1)
=3(×7﹣1)=18.
【点评】本题主要考查了指数及对数的运算性质的应用,属于基础题.
13.(2024秋 浦东新区校级期中)已知函数f(x)=ax(其中a>0,且a≠1).
(1)若f(b)+f(﹣b)=3,求f(2b)+f(﹣2b)的值.
(2)求关于x的方程f(2x)﹣2f(x)+1=0的解.
【考点】有理数指数幂及根式化简运算求值;函数的值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】(1)7;
(2)x=0.
【分析】(1)将f(b)+f(﹣b)代入函数解析式,结合完全平方公式可求得a2b+a﹣2b的值.
(2)将f(2x)﹣2f(x)+1=0代入函数解析式可得具体方程,再结合完全平方公式可解得方程的解.
【解答】解:(1)因为f(x)=ax,
所以f(b)+f(﹣b)=ab+a﹣b=3,
所以(ab+a﹣b)2=a2b+a﹣2b+2=9,
所以a2b+a﹣2b=7,
所以f(2b)+f(﹣2b)=a2b+a﹣2b=7.
(2)因为f(2x)﹣2f(x)+1=a2x﹣2ax+1=0,
则(ax﹣1)2=0,即ax=1,
所以x=0.
【点评】本题主要考查了指数幂的运算性质的应用,属于基础题.
14.(2024秋 张家口期中)近几年3D打印手办深受青少年的喜爱,某工厂计划在2024年利用新技术生产手办,通过调查分析.生产手办全年需投入固定成本12万元,生产x(千件)手办,需另投入成本C(x)(万元).且,由市场调研知每件手办售价90元,且每年内生产的手办当年能全部销售完.
(1)求出2024年的利润L(x)(万元)关于年产量x(千件)的表达式;
(2)2024年年产量为多少(千件)时,该工厂所获利润最大?最大利润是多少?
【考点】指数函数的实际应用.
【专题】应用题;函数思想;数学模型法;函数的性质及应用;数学建模;运算求解.
【答案】(1)L(x);
(2)年产量为10(千件)时工厂所获利润最大,最大利润是8万元.
【分析】(1)分0<x<6和x≥6两种情况,得到函数解析式;
(2)当0<x<6时,利用函数单调性得到当x=4时,L(x)max=4万元,当x≥6时,利用基本不等式求出最大值,比较后得到结论.
【解答】解:(1)当0<x<6时,利润函数L(x)=9x﹣(x2+x)﹣12=﹣x2+8x﹣12;
当x≥6时,利润函数,
所以利润L(x)关于年产量x的解析式为L(x);
(2)若0<x<6,则L(x)=﹣x2+8x﹣12,即L(x)=﹣(x﹣4)2+4,
所以当x=4时,利润函数的最大值为L(x)max=4万元;
若x≥6,则L(x)=﹣(x)+28≤﹣228=8,
当且仅当时,即x=10时,利润函数取得最大值为L(x)max=8万元,
因为8>4,所以2024年年产量为10千件时,该工厂所获利润最大,最大利润是8万元.
【点评】本题考查了利润函数模型应用问题,是基础题.
15.(2024秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
【考点】指数函数的值域.
【专题】函数思想;转化法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)(0,3].
【分析】(1)根据指数函数单调性可得﹣x2+2x≥0,结合二次不等式运算求解即可;
(2)根据二次函数分析可知﹣x2+2x≤1,结合指数函数性质求值域.
【解答】解:(1)因为,且y=3x在定义域R内单调递增,
则﹣x2+2x≥0,解得0≤x≤2,
所以实数x的取值范围是[0,2].
(2)因为﹣x2+2x=﹣(x﹣1)2+1≤1,当且仅当x=1时等号成立,
且y=3x在定义域R内单调递增,则,
又因为,所以f(x)的值域为(0,3].
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 指数运算与指数函数
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
2.(2024秋 朝阳区校级期中)随着我国经济的不断发展,2023年年底某地区农民人均年收入为7000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2030年年底该地区的农民人均年收入为( )
A.7000×1.06×7元 B.7000×1.067元
C.7000×1.06×8元 D.7000×1.068元
3.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
4.(2024秋 宜兴市期中)已知函数,且函数图象不经过第一象限,则b的取值范围是( )
A.(﹣∞,﹣1) B.(﹣∞,﹣1] C.(﹣∞,﹣2] D.(﹣∞,﹣2)
二.多选题(共3小题)
(多选)5.(2024秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
(多选)6.(2024秋 广州期中)已知实数a满足a+a﹣1=4,下列选项中正确的是( )
A.a2+a﹣2=14 B.a﹣a﹣1=2
C. D.
(多选)7.(2024秋 芒市校级期中)下列各式正确的有( )
A. B.
C. D.
三.填空题(共4小题)
8.(2024秋 新吴区校级期中)若,则a2+a﹣2= .
9.(2024秋 朝阳区校级期中)计算: .
10.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= .
11.(2024秋 中山市期中)求值: .
四.解答题(共4小题)
12.(2024秋 西湖区校级期中)求下列各式的值:
(1)log78 (0.2)1﹣log53+2π0 ()﹣6;
(2)已知x﹣1+x=7(x>0),求.
13.(2024秋 浦东新区校级期中)已知函数f(x)=ax(其中a>0,且a≠1).
(1)若f(b)+f(﹣b)=3,求f(2b)+f(﹣2b)的值.
(2)求关于x的方程f(2x)﹣2f(x)+1=0的解.
14.(2024秋 张家口期中)近几年3D打印手办深受青少年的喜爱,某工厂计划在2024年利用新技术生产手办,通过调查分析.生产手办全年需投入固定成本12万元,生产x(千件)手办,需另投入成本C(x)(万元).且,由市场调研知每件手办售价90元,且每年内生产的手办当年能全部销售完.
(1)求出2024年的利润L(x)(万元)关于年产量x(千件)的表达式;
(2)2024年年产量为多少(千件)时,该工厂所获利润最大?最大利润是多少?
15.(2024秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
预习衔接.夯实基础 指数运算与指数函数
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
【考点】指数函数的单调性与最值;对数函数的单调性与最值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】利用指数函数与对数函数的性质分析判断即可.
【解答】解:∵y=3x为R上的增函数,﹣2.5<﹣2.3,
∴0<a3﹣2.5<c=3﹣2.3<1,
又b0,
∴b<a<c.
故选:C.
【点评】本题考查指数函数与对数函数的性质,属于基础题.
2.(2024秋 朝阳区校级期中)随着我国经济的不断发展,2023年年底某地区农民人均年收入为7000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2030年年底该地区的农民人均年收入为( )
A.7000×1.06×7元 B.7000×1.067元
C.7000×1.06×8元 D.7000×1.068元
【考点】指数函数的实际应用.
【专题】应用题;函数思想;数学模型法;函数的性质及应用;数学建模.
【答案】B
【分析】根据指数增长模型计算即可.
【解答】解:设经过x年,该地区的农民人均年收入为y元,
根据题意得,y=7000×1.06x,
从2023年年底到2030年年底共经过了7年,
所以2030年年底该地区的农民人均年收入为7000×1.067元.
故选:B.
【点评】本题考查了指数函数模型应用问题,是基础题.
3.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
【考点】指数函数图象特征与底数的关系.
【专题】数形结合;分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】利用分段函数表示函数y=3|x|,画出函数的大致图象,即可得出答案.
【解答】解:因为y=3|x|,
画出函数的大致图象,如图所示:
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
4.(2024秋 宜兴市期中)已知函数,且函数图象不经过第一象限,则b的取值范围是( )
A.(﹣∞,﹣1) B.(﹣∞,﹣1] C.(﹣∞,﹣2] D.(﹣∞,﹣2)
【考点】指数函数的单调性与最值.
【专题】转化思想;综合法;函数的性质及应用;数据分析.
【答案】C
【分析】由题意利用指数函数的单调性和特殊点,求得b的取值范围.
【解答】解:∵函数的图象经过(0,2+b),
且函数图象不经过第一象限,则2+b≤0,故 b≤﹣2,
故选:C.
【点评】本题主要考查指数函数的单调性和特殊点,属于基础题.
二.多选题(共3小题)
(多选)5.(2024秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
【考点】指数函数图象特征与底数的关系;定义法求解函数的单调性.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】根据题意,结合指数函数、对数函数,以及函数的单调性和反函数的关系,逐项判定,即可求解.
【解答】解:对于A中,函数f(x)=loga(x+1)+loga(x﹣1),则满足,
解得x>1,
即f(x)的定义域为(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,故A不正确;
对于B中,函数f(x)=2ax﹣2﹣1(a>0且a≠1),
令x﹣2=0,可得x=2,
则f(2)=2a0﹣1=1,
所以f(x)恒过定点(2,1),所以B正确;
对于C中,函数,
因为函数y=ex+1为单调递增函数,且y>0
所以为递减函数,则为递增函数,所以C正确;
对于D中,由函数与函数互为反函数,
所以函数与函数y=﹣log2x的图像关于直线y=x对称,所以D正确.
故选:BCD.
【点评】本题主要考查了函数的单调性和奇偶性,考查了反函数的定义,属于基础题.
(多选)6.(2024秋 广州期中)已知实数a满足a+a﹣1=4,下列选项中正确的是( )
A.a2+a﹣2=14 B.a﹣a﹣1=2
C. D.
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】ACD
【分析】根据a2+a﹣2=(a+a﹣1)2﹣2a a﹣1即可判断A;
根据(a﹣a﹣1)2=a2+a﹣2﹣2a a﹣1即可判断B,注意符号;
根据即可判断C;
利用立方和公式即可判断D.
【解答】解:因为a+a﹣1=4,所以a>0,a2+a﹣2=(a+a﹣1)2﹣2a a﹣1=16﹣2=14,故A正确;
(a﹣a﹣1)2=a2+a﹣2﹣2a a﹣1=12,所以,故B错误;
,
又a>0,所以,则,故C正确;,故D正确.
故选:ACD.
【点评】本题考查了完全平方公式和立方和公式,是基础题.
(多选)7.(2024秋 芒市校级期中)下列各式正确的有( )
A. B.
C. D.
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】运用根式的化简方法直接求解即可.
【解答】解:∵∴A项错误;
∵,
∴B项正确;
∵,∴C项正确;
∵,∴D项正确.
故选:BCD.
【点评】本题主要考查了根式的化简,属于基础题.
三.填空题(共4小题)
8.(2024秋 新吴区校级期中)若,则a2+a﹣2= 47 .
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】47.
【分析】结合指数幂的运算性质即可求解.
【解答】解:若,
则a+a﹣1+2=9,即a+a﹣1=7,
则a2+a﹣2+2=49,即a2+a﹣2=47.
故答案为:47.
【点评】本题主要考查了指数幂的运算性质,属于基础题.
9.(2024秋 朝阳区校级期中)计算: ﹣19681 .
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】﹣19681.
【分析】根据对数的运算性质和指数幂的运算性质求解.
【解答】解:原式=log39+(﹣27)3(﹣19683)=2+(﹣19683)=﹣19681.
故答案为:﹣19681.
【点评】本题主要考查了对数的运算性质,考查了指数幂的运算性质,属于基础题.
10.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= ﹣5 .
【考点】指数函数的单调性与最值.
【专题】转化思想;定义法;不等式的解法及应用;运算求解.
【答案】﹣5.
【分析】根据y=2x在R上单调递增,判断大小列不等式进行解答即可.
【解答】解:不等式可化为23﹣3x,
因为y=2x在R上单调递增,
所以x2﹣2x﹣3<3﹣3x,整理得x2+x﹣6<0,
由题意知两不等式的解集相同,则a=1,b=﹣6,
所以a+b=﹣5.
故答案为:﹣5.
【点评】本题考查了函数与不等式的应用问题,是基础题.
11.(2024秋 中山市期中)求值: .
【考点】有理数指数幂及根式化简运算求值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】.
【分析】根据根式、分数指数幂运算、零指数幂运算得出结果.
【解答】解: .
故答案为:.
【点评】本题主要考查了有理数指数幂的运算性质,属于基础题.
四.解答题(共4小题)
12.(2024秋 西湖区校级期中)求下列各式的值:
(1)log78 (0.2)1﹣log53+2π0 ()﹣6;
(2)已知x﹣1+x=7(x>0),求.
【考点】有理数指数幂及根式化简运算求值.
【专题】综合法;函数的性质及应用;能力层次;运算求解.
【答案】(1);
(2)18.
【分析】(1)结合指数及对数的运算性质进行化简即可求解;
(2)结合指数幂的运算性质即可求解.
【解答】解:(1)log78 (0.2)1﹣log53+2π0 ()﹣6
=﹣162
=﹣1616
;
(2)因为x﹣1+x=7,x>0,
则(x)2=x+x﹣1+2=9,
则x3,
()3+(x)3=(x)(x+x﹣1﹣1)
=3(×7﹣1)=18.
【点评】本题主要考查了指数及对数的运算性质的应用,属于基础题.
13.(2024秋 浦东新区校级期中)已知函数f(x)=ax(其中a>0,且a≠1).
(1)若f(b)+f(﹣b)=3,求f(2b)+f(﹣2b)的值.
(2)求关于x的方程f(2x)﹣2f(x)+1=0的解.
【考点】有理数指数幂及根式化简运算求值;函数的值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】(1)7;
(2)x=0.
【分析】(1)将f(b)+f(﹣b)代入函数解析式,结合完全平方公式可求得a2b+a﹣2b的值.
(2)将f(2x)﹣2f(x)+1=0代入函数解析式可得具体方程,再结合完全平方公式可解得方程的解.
【解答】解:(1)因为f(x)=ax,
所以f(b)+f(﹣b)=ab+a﹣b=3,
所以(ab+a﹣b)2=a2b+a﹣2b+2=9,
所以a2b+a﹣2b=7,
所以f(2b)+f(﹣2b)=a2b+a﹣2b=7.
(2)因为f(2x)﹣2f(x)+1=a2x﹣2ax+1=0,
则(ax﹣1)2=0,即ax=1,
所以x=0.
【点评】本题主要考查了指数幂的运算性质的应用,属于基础题.
14.(2024秋 张家口期中)近几年3D打印手办深受青少年的喜爱,某工厂计划在2024年利用新技术生产手办,通过调查分析.生产手办全年需投入固定成本12万元,生产x(千件)手办,需另投入成本C(x)(万元).且,由市场调研知每件手办售价90元,且每年内生产的手办当年能全部销售完.
(1)求出2024年的利润L(x)(万元)关于年产量x(千件)的表达式;
(2)2024年年产量为多少(千件)时,该工厂所获利润最大?最大利润是多少?
【考点】指数函数的实际应用.
【专题】应用题;函数思想;数学模型法;函数的性质及应用;数学建模;运算求解.
【答案】(1)L(x);
(2)年产量为10(千件)时工厂所获利润最大,最大利润是8万元.
【分析】(1)分0<x<6和x≥6两种情况,得到函数解析式;
(2)当0<x<6时,利用函数单调性得到当x=4时,L(x)max=4万元,当x≥6时,利用基本不等式求出最大值,比较后得到结论.
【解答】解:(1)当0<x<6时,利润函数L(x)=9x﹣(x2+x)﹣12=﹣x2+8x﹣12;
当x≥6时,利润函数,
所以利润L(x)关于年产量x的解析式为L(x);
(2)若0<x<6,则L(x)=﹣x2+8x﹣12,即L(x)=﹣(x﹣4)2+4,
所以当x=4时,利润函数的最大值为L(x)max=4万元;
若x≥6,则L(x)=﹣(x)+28≤﹣228=8,
当且仅当时,即x=10时,利润函数取得最大值为L(x)max=8万元,
因为8>4,所以2024年年产量为10千件时,该工厂所获利润最大,最大利润是8万元.
【点评】本题考查了利润函数模型应用问题,是基础题.
15.(2024秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
【考点】指数函数的值域.
【专题】函数思想;转化法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)(0,3].
【分析】(1)根据指数函数单调性可得﹣x2+2x≥0,结合二次不等式运算求解即可;
(2)根据二次函数分析可知﹣x2+2x≤1,结合指数函数性质求值域.
【解答】解:(1)因为,且y=3x在定义域R内单调递增,
则﹣x2+2x≥0,解得0≤x≤2,
所以实数x的取值范围是[0,2].
(2)因为﹣x2+2x=﹣(x﹣1)2+1≤1,当且仅当x=1时等号成立,
且y=3x在定义域R内单调递增,则,
又因为,所以f(x)的值域为(0,3].
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
