第二章 相交线与平行线(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 第二章 相交线与平行线(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 424.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 13:35:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章 相交线与平行线
一.选择题(共10小题)
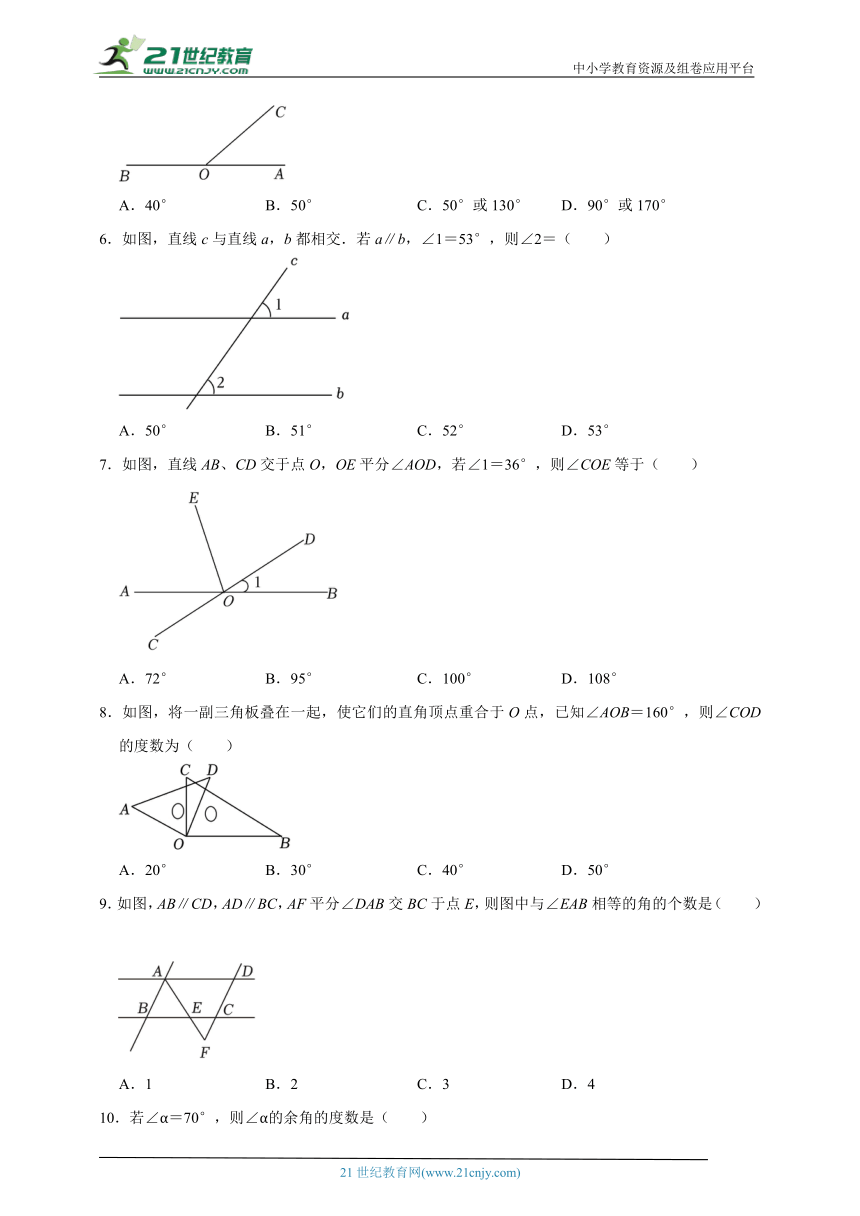
1.如图,已知直线a∥b,现将含45°角的直角三角板放入平行线之间,两个锐角顶点分别落在两条直线上.若∠1=23°,则∠2的度数为( )
A.68° B.67° C.23° D.22°
2.如图所示,D是直线EF上一点,CD⊥EF,∠1=∠2,则下列结论中错误的是( )
A.∠ADF与∠2互补 B.∠BDC与∠1互余
C.∠ADB与∠2相等 D.DC平分∠ADB
3.如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( )
A.75° B.70° C.65° D.60°
4.如图所示,已知AD∥BC,则下列结论:①∠1=∠2;②∠2=∠3;③∠6=∠8;④∠5=∠8;⑤∠2=∠4,其中一定正确的( )
A.② B.②③⑤ C.①③④ D.②④
5.如图,射线OC的端点O在直线AB上,∠AOC=40°,点D在平面内,∠BOD与∠AOC互余,则∠DOC的度数为( )
A.40° B.50° C.50°或130° D.90°或170°
6.如图,直线c与直线a,b都相交.若a∥b,∠1=53°,则∠2=( )
A.50° B.51° C.52° D.53°
7.如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=36°,则∠COE等于( )
A.72° B.95° C.100° D.108°
8.如图,将一副三角板叠在一起,使它们的直角顶点重合于O点,已知∠AOB=160°,则∠COD的度数为( )
A.20° B.30° C.40° D.50°
9.如图,AB∥CD,AD∥BC,AF平分∠DAB交BC于点E,则图中与∠EAB相等的角的个数是( )
A.1 B.2 C.3 D.4
10.若∠α=70°,则∠α的余角的度数是( )
A.20° B.30° C.70° D.110°
二.填空题(共6小题)
11.已知∠A=38°28',那么∠A的余角是 .
12.如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的度数为 .
13.若∠α=50°10',则它的余角是 .
14.将一副三角板中的两块直角三角尺按如图方式放置(其中∠ABC=45°,∠D=60°),固定三角尺ABC,将三角尺BDE以每秒30°的速度绕点B按逆时针方向旋转180°停止.在这个过程中,当运动时间为 秒时,三角尺BDE的一边与三角尺ABC的某一边平行(不共线).
15.古希腊数学家埃拉托色尼发现,如图,夏至正午时分太阳光线直射进点A处塞尼城的一口深井,说明太阳光线过圆心O.而同一经度上另外一点B处的亚历山大城一个方尖塔却会投影下一定长度的阴影,他测得方尖塔与太阳光线的夹角为7.2°,方尖塔延长线BO经过圆心O.由太阳光线是平行光线,得到深井延长线AO和方尖塔延长线BO所夹圆心角的度数.因而得到球周长约为40000km(接近真实值40009km).埃拉托色尼计算地球周长时用到的原理是 .
16.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 (只填出一种即可)的条件.
三.解答题(共8小题)
17.如图,过点O在∠AOB内部作射线OC.OE,OF分别平分∠AOC和∠BOC,∠AOC与∠AOB互补,
(1)如图1,若∠AOC=70°,求∠EOF的角度;
(2)如图2,OD平分∠AOB.
①若∠AOC﹣3∠COD=32°,求∠EOF的角度;
②试探索:当k为何值时,的值时一个定值,并求出这个定值.
18.直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠BOD=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=30°,求∠BOD的度数.
19.定义:从∠α(90°<α<180°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为补角,则称该射线为∠α的“好线”.
如图,点O在直线AB上,OC、OD在直线AB上方,且OC⊥OD,射线OE是∠AOD的“好线”.
(1)若∠BOD=26°,且OE在∠COD内部,则∠COE= °;
(2)若OE恰好平分∠AOC,请求出∠BOD的度数;
(3)若OF是∠AOE的平分线,OG是∠BOC的平分线,请画出图形,探究∠EOF与∠DOG的数量关系,并说明理由.
20.综合与探究
问题情境:
数学活动课上,老师以直线AB上一点O为端点作射线OC,OD,OM,ON,使OM平分∠AOC,ON平分∠BOD,若∠COD=α,求∠MOC+∠DON的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当∠COD=90°时,则∠MOC+∠DON的度数为 ;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺60°角的顶点放在点O处,即当∠COD=60°时,请你在图3中求∠MOC+∠DON的度数;
数学思考:
(3)请你在图1中,求∠MOC+∠DON的度数(用含有α的式子表示).
21.已知一副三角板按图1所示摆放,∠AOB=∠OCD=90°,∠OAB=45°,∠COD=60°,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧.
(1)保持△AOB不动,将△COD绕点O旋转至如图2所示的位置,则∠BOC﹣∠AOD= ;
(2)保持△AOB不动,将△COD绕点O逆时针方向旋转n°(n<180°),试探究∠BOC与∠AOD的数量关系;
(3)如图3,若△COD按每分钟15°的速度绕点O逆时针方向旋转,同时,△AOB按每分钟9°的速度也绕点O逆时针方向旋转,多少分钟时,OD边第一次与OB边重合?
22.一个角的余角比它的补角的还少50°,求这个角的度数.
23.数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE= ,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
24.阅读下面材料,解决下列问题:
材料:
如图①,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,则图中哪些角互为余角?
解:因为点A,O,B在同一条直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以.
所以∠COD与∠COE互为余角.
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
问题:
(1)如图②,已知,∠AOB=140°,射线OC是∠AOB内部任意一条射线,射线OM,ON分别平分∠AOC,∠BOC.求∠MON的度数(类比以上材料写解答过程);
(2)如图②,射线OC是∠AOB内部任意一条射线,射线OM,ON分别平分∠AOC,∠BOC.则∠MON与∠AOB之间的数量关系是 ;
(3)若把(1)中的条件“射线OC是∠AOB内部任意一条射线”更改为“射线OC是∠AOB外部任意一条射线”,其他条件保持不变,直接写出∠MON的度数.
第二章 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】根据题意可得:∠3=45°,从而利用角的和差关系可得∠ABC=68°,然后利用平行线的性质可得∠2=∠ABC=68°,即可解答.
【解答】解:如图:
由题意得:∠3=45°,
∵∠1=23°,
∴∠ABC=∠1+∠3=68°,
∵a∥b,
∴∠2=∠ABC=68°,
故选:A.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
2.【答案】C
【分析】A.利用补角的定义即可得到答案;
B.利用余角的定义即可得到答案;
C.没有可以验证∠ADB=∠2相等的条件;
D.利用等角的补角相等即可得出答案.
【解答】解:A.∵∠ADF+∠1=180°,∠1=∠2,
∴∠ADF+∠2=180°,故本选项不符合题意;
B.∵CD⊥EF,
∴∠BDC+∠2=90°,
∵∠1=∠2,
∴∠BDC+∠1=90°,故本选项不符合题意;
C.∠ADB≠∠2,故本选项符合题意;
D..∵CD⊥EF,
∴∠BDC+∠2=90°,
同理可得∠ADC+∠1=90°,
∵∠1=∠2,
∴∠BDC=∠ADC,
∴CD平分∠ABD,故本选项不符合题意;
故选:C.
【点评】本题主要考查余角和补角以及垂线的定义,解决此题的关键是熟练掌握这些知识点并灵活运用.
3.【答案】A
【分析】根据平行线的性质可得∠ABC=∠D=45°,再根据三角形内角与外角的关系可得∠1的度数.
【解答】解:如图,∵AB∥DE,
∴∠ABC=∠D=45°,
又∵∠A=30°,
∴∠1=∠A+∠ABC=75°,
故选:A.
【点评】此题主要考查了平行线的性质以及三角形外角性质的应用,关键是掌握两直线平行,同位角相等.
4.【答案】A
【分析】根据平行线的性质判断即可.
【解答】解:∵AD∥BC,
∴∠2=∠3,
故选:A.
【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.
5.【答案】D
【分析】先根据互为余角的定义求出∠BOD的度数,再分两种情况讨论:当∠BOD在直线AB上方时;当∠BOD在直线AB下方时;分别计算即可.
【解答】解:∵∠AOC=40°,∠BOD与∠AOC互余,
∴∠BOD=90°﹣∠AOC=90°﹣40°=50°,
当∠BOD在直线AB上方时,
∠DOC=180°﹣∠BOD﹣∠AOC=180°﹣50°﹣40°=90°;
当∠BOD在直线AB下方时,
∠AOD=180°﹣∠BOD=180°﹣50°=130°,
∴∠DOC=∠AOD+∠AOC=130°+40°=170°;
综上,∠DOC的度数为90°或170°,
故选:D.
【点评】本题考查了余角和补角,角的和差,注意分类讨论思想的运用.
6.【答案】D
【分析】根据平行线的性质可得∠1=∠2,根据∠1=53°解答即可.
【解答】解:∵a∥b,
∴∠1=∠2,
∵∠1=53°,
∴∠2=53°.
故选:D.
【点评】本题考查的是平行线的性质,解题的关键是熟练掌握平行线的性质并灵活运用;平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.
7.【答案】D
【分析】根据邻补角的概念求出∠AOD,根据角平分线的定义求出∠DOE,再根据邻补角的概念计算,得到答案.
【解答】解:∵∠1=36°,
∴∠AOD=180°﹣∠1=144°,
∵OE平分∠AOD,
∴∠DOE∠AOD=72°,
∴∠COE=180°﹣∠DOE=108°,
故选:D.
【点评】本题考查的是邻补角的概念、角平分线的定义,掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解题的关键.
8.【答案】A
【分析】由∠AOC=∠AOB﹣∠BOC,求出∠AOC,再由∠COD=∠AOD﹣∠AOC,即可计算.
【解答】解:∵∠AOC=∠AOB﹣∠BOC,
∴∠AOC=160°﹣90°=70°,
∵∠COD=∠AOD﹣∠AOC,
∴∠COD=90°﹣70°=20°.
故选:A.
【点评】本题考查角的计算,关键是由角的和差表示出有关的角即可.
9.【答案】D
【分析】由角平分线定义得到∠BAE=∠DAE,由平行线的性质推出∠EAB=∠F,∠DAE=∠AEB,由对顶角的性质得到∠CEF=∠AEB,即可得到答案.
【解答】解:∵AF平分∠DAB,
∴∠BAE=∠DAE,
∵AB∥CD,
∴∠EAB=∠F,
∵AD∥BC,
∴∠DAE=∠AEB,
∵∠CEF=∠AEB,
∴与∠EAB相等的角是∠DAE、∠F,∠AEB、∠CEF,个数是4个.
故选:D.
【点评】本题考查平行线是性质,关键是由平行线的性质推出∠EAB=∠F,∠DAE=∠AEB.
10.【答案】A
【分析】根据余角的定义进行计算即可.
【解答】解:∵∠α=70°,
∴∠α的余角的度数是:90°﹣70°=20°,
故选:A.
【点评】本题考查了余角的定义,两角之和等于90°,则这两个角互为余角.
二.填空题(共6小题)
11.【答案】51°32′.
【分析】根据余角的定义列式计算即可.
【解答】解:∵∠A=38°28′,
∴其余角为:90°﹣38°28′=51°32′,
故答案为:51°32′.
【点评】本题主要考查余角的定义,此定义是基础且重要知识点,必须掌握.
12.【答案】54°.
【分析】先求出∠DOC,再求出∠BOC.
【解答】解:∵∠AOC=90°,∠AOD=126°,
∴∠DOC=∠AOD﹣∠AOC=126°﹣90°=36°,
∵∠BOD=90°,
∴∠BOC=∠BOD﹣∠COD=90°﹣36°=54°.
故答案为:54°.
【点评】本题主要考查角的和差和余角的性质,解决本题的关键是找出互余的角.
13.【答案】39°50'.
【分析】用90°减去∠α的度数,即可求出它的余角的度数.
【解答】解:∵∠α=50°10',
∴它的余角=90°﹣50°10'=39°50'.
故答案为:39°50'.
【点评】本题主要考查余角的意义和度分秒的换算,熟练掌握求一个角的余角的方法是解决问题的关键.
14.【答案】0.5或1.5或3.5或4.5或5.
【分析】需要分类讨论,当DE∥AB时,BD∥AC时,当DE∥AC时,当BE∥AC时,当DE∥BC时,分别画出图形,根据平行线的性质求解即可.
【解答】解:当DE∥AB时,如图1,
此时∠ABE=∠E=30°,
∴∠CBE=15°,
t=15°÷30°=0.5;
当BD∥AC时,如图2,
此时∠DBC=45°,
t=45°÷30°=1.5;
当DE∥AC时,如图3,
此时,∠EBC=60°+45°=105°,
t=105°÷30°=3.5;
当BE∥AC时,如图4,
此时∠EBC=90°+45°=135°,
∴t=135°÷30°=4.5;
当DE∥BC时,如图5,
此时∠EBC=90°+60°=150°,
t=150°÷30°=5,
故答案为:0.5或1.5或3.5或4.5或5.
【点评】本题主要考查平行线的性质,分类讨论思想和数形结合思想,根据题意进行正确的分类讨论并作出图形是解题关键.
15.【答案】两直线平行,内错角相等.
【分析】根据平行线的性质得出∠AOB=∠MCO=7.2°,即可得到答案.
【解答】解:∵太阳光线是平行光线,
∴AO∥CM,
∴∠AOB=∠MCO=7.2°,
∴用到的原理是两直线平行,内错角相等.
故答案为:两直线平行,内错角相等.
【点评】本题主要考查了平行线的性质,掌握平行线的性质是解题关键.
16.【答案】∠ACD=90°(答案不唯一).
【分析】由平行线的判定,即可得到答案.
【解答】解:∵AB⊥AC,
∴∠BAC=90°,
若∠ACD=90°,则∠BAC=∠ACD,
∴AB∥CD,
∴要使AB∥CD,可添加∠ACD=90°(答案不唯一).
故答案为:∠ACD=90°(答案不唯一).
【点评】本题考查平行线的判定,关键是掌握平行线的判定方法.
三.解答题(共8小题)
17.【答案】(1)∠EOF=55°.
(2)①∠EOF=56°.
②k时,定值为2.
【分析】(1)由平分线得∠BOF=∠COF=α,∠COE=∠AOE=35°,由∠AOC与∠AOB互补得70°+70°+2α=180°,再计算即可.
(2)①设∠COD=2m,所以∠AOC=32°+6m,由角平分线得∠COE=∠EOA=16°+3m,∠BOF=∠COF=n,再计算即可.
②∠EOA=x+y,由角平分线得∠BOD=∠AOD,故2n+x=2y+x,所以n=y.化简得当2k﹣1=0时,即k时,原式为定值,再计算即可.
【解答】解:(1)∵OF平分∠BOC,
∴∠BOF=∠COF=α.
∵OE平分∠AOC,
∴∠COE=∠AOE=35°,
∵∠AOC与∠AOB互补,
∴70°+70°+2α=180°,
∴α=20°,
∴∠EOF=35°+20°=55°.
(2)①设∠COD=2m,
∵∠AOC﹣3∠COD=32°,
∴∠AOC=32°+6m,
∵OE平分∠AOC,
∴∠COE=∠EOA=16°+3m,
∴∠DOE=16°+3m﹣2m=16°+m.
∵OF平分∠BOC,
∴∠BOF=∠COF=n.
∵∠AOC与∠AOB互补,
∴32°+6m+32°+6m+2n=180°,
∴6m+n=58°①.
∵OD平分∠AOB,
∴∠BOD=∠AOD,
∴2n+2m=16°+m+16°+3m,
∴n﹣m=16°②,
由①②得m=6°,n=22°,
∴∠EOF=n+16+3m=56°.
②当k=时,的值时一个定值.
理由如下:
∴∠EOA=x+y,
∵OD平分∠AOB,
∴∠BOD=∠AOD,
∴2n+x=2y+x,
∴n=y.
∴
当2k﹣1=0时,即k时,
原式
=2.
答:k时,定值为2.
【点评】本题考查了余角和补角的知识,看图表示出角的度数是解题关键.
18.【答案】(1)56°;
(2)80°.
【分析】(1)根据已知条件得到∠BOF=∠DOF﹣∠BOD=90°﹣68°=22°,角平分线得到,再根据∠EOF=∠BOF+∠BOE,即可得解;
(2)角平分线和平角得到,再根据角平分线,得到,再利用∠BOF=∠EOF﹣∠BOE,进行计算即可.
【解答】解:(1)∵∠DOF=90°,∠BOD=68°,
∴∠BOF=∠DOF﹣∠BOD=90°﹣68°=22°,
∵OE平分∠BOD,
∴,
∴∠EOF=∠BOF+∠BOE=22°+34°=56°;
(2)∵OE平分∠BOD,
∴,
∴,
∵OF平分∠COE,
∴
,
∵∠BOF=∠EOF﹣∠BOE,
∴,
∴∠BOD=80°.
【点评】本题考查几何图形中角度的计算.正确的识图,理清角度之间的和差,倍数关系,是解题的关键.
19.【答案】(1)38°或64;
(2)∠BOD=30°;
(3)∠EOF=2∠DOG或∠EOF+∠DOG=45°.
【分析】(1)分两种情况,即当∠DOE+∠AOD=180°和∠AOE+∠AOD=180°时,分别画出相应的图形,由角平分线的定义以及图形中角的和差关系进行解答即可;
(2)根据平角的定义以及角平分线的定义进行计算即可;
(3)分(1)中的两种情况进行解答,分别用∠BOD表示∠EOF,∠DOG,进而答案即可.
【解答】解:(1)如图1﹣1,由于射线OE是∠AOD的“好线”,
当∠DOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠DOE=∠BOD=26°,
∵OC⊥OD,
∴∠COD=90°,
∴∠COE=90°﹣26°=64°,
如图1﹣2,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠AOE=∠BOD=26°,
∴∠COE=180°﹣26°﹣26°﹣90°=38°,
因此∠COE=38°或∠COE=64°,
故答案为:38°或64;
(2)若OE恰好平分∠AOC,
∴∠AOE=∠COE=∠BOD,
∴∠BOD(180°﹣90°)=30°;
(3)∠EOF=2∠DOG或∠EOF+∠DOG=45°,理由如下:
如图2﹣1,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠AOE=∠BOD,
∵OF是∠AOE的平分线,
∴∠EOF∠AOE∠BOD,
∴OG是∠BOC的平分线,
∴∠BOG∠BOC(90°+∠BOD)=45°∠BOD,
∴∠DOG=∠BOG﹣∠BOD=45°∠BOD,
∴∠EOF+∠DOG=45°,
如图2﹣2,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠EOD=180°,
∴∠DOE=∠BOD,
∴∠DOG∠BOC﹣∠BOD
(90°+∠BOD)﹣∠BOD
=45°∠BOD,
∠EOF∠AOE(180°﹣2∠BOD)
=90°﹣∠BOD,
∴∠EOF=2∠DOG,
综上所述∠EOF=2∠DOG或∠EOF+∠DOG=45°.
【点评】本题考查角平分线,余角与补角,掌握角平分线的定义,余角与补角的定义,理解“好线”的定义是正确解答的关键.
20.【答案】(1)45°;(2)60°;(3).
【分析】(1)求得∠AOC+∠BOD=90°,利用角平分线的定义得,据此求解即可;
(2)求得∠AOC+∠BOD=120°,利用角平分线的定义得,据此求解即可;
(3)求得∠AOC+∠BOD=180°﹣α,利用角平分线的定义得求解即可.
【解答】解:(1)因为∠COD=90°,所以∠AOC+∠BOD=90°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
故答案为:45°;
(2)因为∠COD=60°,所以∠AOC+∠BOD=120°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
(3)因为∠COD=α,所以∠AOC+∠BOD=180°﹣α,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
.
【点评】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
21.【答案】(1)30°.
(2)∠BOC﹣∠AOD=30°,或∠BOC+∠AOD=30°,或∠AOD﹣∠BOC=30°.
(3)25分钟时,OD边第一次与OB边重合.
【分析】(1)由∠BOC=∠BOA﹣∠COA,∠AOD=∠COD﹣∠COA,得∠BOC﹣∠AOD=(∠BOA﹣∠COA)﹣(∠COD﹣∠COA)=∠BOA﹣∠COD=90°﹣60°=30°.
(2)设∠COA=α,分三种情况讨论:①当0°<α≤60°时,②当60°<α≤90°时,③当90°<α≤180°时,把∠BOC和∠AOD用含α的式子表示,再计算即可.
(3)先求出OD按每分钟15°的速度旋转,OB按每分钟9°的速度,再按照追击问题得150÷(15﹣9)=25(分钟).
【解答】解:(1)∵∠BOC=∠BOA﹣∠COA,
又∠AOD=∠COD﹣∠COA,
∴∠BOC﹣∠AOD=(∠BOA﹣∠COA)﹣(∠COD﹣∠COA)=∠BOA﹣∠COD=90°﹣60°=30°.
故答案为:30°.
(2)设∠COA=α,
①当0°<α≤60°时,如图a,由(1)得∴∠BOC﹣∠AOD=30°.
②当60°<α≤90°时,如图b,
∠BOC=90°﹣α,∠AOD=α﹣60°,
∴∠BOC+∠AOD=90°﹣α+α﹣60°=30°.
③当90°<α≤180°时,如图c,
∠BOC=60°﹣α,∠AOD=90°﹣α,
∴∠AOD﹣∠BOC=90°﹣α﹣(60°﹣α)=30°.
综上所述,∠BOC﹣∠AOD=30°,或∠BOC+∠AOD=30°,或∠AOD﹣∠BOC=30°.
(3)∵△COD按每分钟15°的速度旋转,
∴OD按每分钟15°的速度旋转,
同理,OB按每分钟9°的速度,
∵∠BOD=∠BOA+∠AOD=90°+60°=150°,
∴150÷(15﹣9)=25(分钟).
答:25分钟时,OD边第一次与OB边重合.
【点评】本题考查了余角和补角的知识,利用数形结合,列出算式计算是解题关键.
22.【答案】这个角的度数是60°.
【分析】设这个角为x,则余角为90°﹣x,补角为180°﹣x,根据题意表述可列出方程,解出即可.
【解答】解:设这个角为x,则余角为90°﹣x,补角为180°﹣x,
由题意得:90°﹣x(180°﹣x)﹣50°,
解得:x=60°.
∴这个角的度数是60°.
【点评】本题考查在余角和补角的知识基础上,考查一元一次方程的应用,难度不大,关键是运用方程思想解题.
23.【答案】见试题解答内容
【分析】(1)当∠DCE=30°时,利用互余计算出∠BCD,然后可得到∠ACB+∠DCE的度数;若∠DCE为任意锐角时,利用∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,然后计算出∠ACB+∠DCE=180°;
(2)利用周角定义得到∠ACD+∠ECB+∠ACB+∠DCE=360°所以∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=180°.
【解答】解:(1)∠ACB+∠DCE=180°;
若∠DCE为任意锐角时,∠ACB+∠DCE=180°,
理由如下:∵∠ACE+∠DCE=90°,
∠BCD+∠DCE=90°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°;
(2)∠ACB+∠DCE=180°.
理由如下:∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°.
故答案为30°.
【点评】本题考查了余角和补角:等角的补角相等.等角的余角相等;余角和补角计算的应用,常常与等式的性质、等量代换相关联.
24.【答案】(1)∠MON=70°;
(2)∠MON∠AOB;
(3)∠MON=110°.
【分析】(1)已知∠AOB=140°,射线OC是∠AOB内部任意一条射线,可得∠AOC+∠BOC的度数,因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON的度数,即∠MON的度数;
(2)因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)∠AOB,即∠MON∠AOB;
(3)已知∠AOB=140°,射线OC是∠AOB外部任意一条射线,可得∠AOC+∠BOC的度数,因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON的度数,即∠MON的度数.
【解答】解:(1)∵∠AOB=140°,射线OC是∠AOB内部任意一条射线,
∴∠AOC+∠BOC=140°,
又∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)=70°,
∴∠MON=70°;
(2)∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)∠AOB,
∴∠MON∠AOB,
故答案为:∠MON∠AOB;
(3)∵∠AOB=140°,射线OC是∠AOB外部任意一条射线,
∴∠AOC+∠BOC=220°,
又∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)=110°,
∴∠MON=110°.
【点评】本题考查了角平分线,关键是掌握角平分线的定义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 相交线与平行线
一.选择题(共10小题)
1.如图,已知直线a∥b,现将含45°角的直角三角板放入平行线之间,两个锐角顶点分别落在两条直线上.若∠1=23°,则∠2的度数为( )
A.68° B.67° C.23° D.22°
2.如图所示,D是直线EF上一点,CD⊥EF,∠1=∠2,则下列结论中错误的是( )
A.∠ADF与∠2互补 B.∠BDC与∠1互余
C.∠ADB与∠2相等 D.DC平分∠ADB
3.如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( )
A.75° B.70° C.65° D.60°
4.如图所示,已知AD∥BC,则下列结论:①∠1=∠2;②∠2=∠3;③∠6=∠8;④∠5=∠8;⑤∠2=∠4,其中一定正确的( )
A.② B.②③⑤ C.①③④ D.②④
5.如图,射线OC的端点O在直线AB上,∠AOC=40°,点D在平面内,∠BOD与∠AOC互余,则∠DOC的度数为( )
A.40° B.50° C.50°或130° D.90°或170°
6.如图,直线c与直线a,b都相交.若a∥b,∠1=53°,则∠2=( )
A.50° B.51° C.52° D.53°
7.如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=36°,则∠COE等于( )
A.72° B.95° C.100° D.108°
8.如图,将一副三角板叠在一起,使它们的直角顶点重合于O点,已知∠AOB=160°,则∠COD的度数为( )
A.20° B.30° C.40° D.50°
9.如图,AB∥CD,AD∥BC,AF平分∠DAB交BC于点E,则图中与∠EAB相等的角的个数是( )
A.1 B.2 C.3 D.4
10.若∠α=70°,则∠α的余角的度数是( )
A.20° B.30° C.70° D.110°
二.填空题(共6小题)
11.已知∠A=38°28',那么∠A的余角是 .
12.如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的度数为 .
13.若∠α=50°10',则它的余角是 .
14.将一副三角板中的两块直角三角尺按如图方式放置(其中∠ABC=45°,∠D=60°),固定三角尺ABC,将三角尺BDE以每秒30°的速度绕点B按逆时针方向旋转180°停止.在这个过程中,当运动时间为 秒时,三角尺BDE的一边与三角尺ABC的某一边平行(不共线).
15.古希腊数学家埃拉托色尼发现,如图,夏至正午时分太阳光线直射进点A处塞尼城的一口深井,说明太阳光线过圆心O.而同一经度上另外一点B处的亚历山大城一个方尖塔却会投影下一定长度的阴影,他测得方尖塔与太阳光线的夹角为7.2°,方尖塔延长线BO经过圆心O.由太阳光线是平行光线,得到深井延长线AO和方尖塔延长线BO所夹圆心角的度数.因而得到球周长约为40000km(接近真实值40009km).埃拉托色尼计算地球周长时用到的原理是 .
16.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 (只填出一种即可)的条件.
三.解答题(共8小题)
17.如图,过点O在∠AOB内部作射线OC.OE,OF分别平分∠AOC和∠BOC,∠AOC与∠AOB互补,
(1)如图1,若∠AOC=70°,求∠EOF的角度;
(2)如图2,OD平分∠AOB.
①若∠AOC﹣3∠COD=32°,求∠EOF的角度;
②试探索:当k为何值时,的值时一个定值,并求出这个定值.
18.直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠BOD=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=30°,求∠BOD的度数.
19.定义:从∠α(90°<α<180°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为补角,则称该射线为∠α的“好线”.
如图,点O在直线AB上,OC、OD在直线AB上方,且OC⊥OD,射线OE是∠AOD的“好线”.
(1)若∠BOD=26°,且OE在∠COD内部,则∠COE= °;
(2)若OE恰好平分∠AOC,请求出∠BOD的度数;
(3)若OF是∠AOE的平分线,OG是∠BOC的平分线,请画出图形,探究∠EOF与∠DOG的数量关系,并说明理由.
20.综合与探究
问题情境:
数学活动课上,老师以直线AB上一点O为端点作射线OC,OD,OM,ON,使OM平分∠AOC,ON平分∠BOD,若∠COD=α,求∠MOC+∠DON的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当∠COD=90°时,则∠MOC+∠DON的度数为 ;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺60°角的顶点放在点O处,即当∠COD=60°时,请你在图3中求∠MOC+∠DON的度数;
数学思考:
(3)请你在图1中,求∠MOC+∠DON的度数(用含有α的式子表示).
21.已知一副三角板按图1所示摆放,∠AOB=∠OCD=90°,∠OAB=45°,∠COD=60°,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧.
(1)保持△AOB不动,将△COD绕点O旋转至如图2所示的位置,则∠BOC﹣∠AOD= ;
(2)保持△AOB不动,将△COD绕点O逆时针方向旋转n°(n<180°),试探究∠BOC与∠AOD的数量关系;
(3)如图3,若△COD按每分钟15°的速度绕点O逆时针方向旋转,同时,△AOB按每分钟9°的速度也绕点O逆时针方向旋转,多少分钟时,OD边第一次与OB边重合?
22.一个角的余角比它的补角的还少50°,求这个角的度数.
23.数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE= ,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
24.阅读下面材料,解决下列问题:
材料:
如图①,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,则图中哪些角互为余角?
解:因为点A,O,B在同一条直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以.
所以∠COD与∠COE互为余角.
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
问题:
(1)如图②,已知,∠AOB=140°,射线OC是∠AOB内部任意一条射线,射线OM,ON分别平分∠AOC,∠BOC.求∠MON的度数(类比以上材料写解答过程);
(2)如图②,射线OC是∠AOB内部任意一条射线,射线OM,ON分别平分∠AOC,∠BOC.则∠MON与∠AOB之间的数量关系是 ;
(3)若把(1)中的条件“射线OC是∠AOB内部任意一条射线”更改为“射线OC是∠AOB外部任意一条射线”,其他条件保持不变,直接写出∠MON的度数.
第二章 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】根据题意可得:∠3=45°,从而利用角的和差关系可得∠ABC=68°,然后利用平行线的性质可得∠2=∠ABC=68°,即可解答.
【解答】解:如图:
由题意得:∠3=45°,
∵∠1=23°,
∴∠ABC=∠1+∠3=68°,
∵a∥b,
∴∠2=∠ABC=68°,
故选:A.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
2.【答案】C
【分析】A.利用补角的定义即可得到答案;
B.利用余角的定义即可得到答案;
C.没有可以验证∠ADB=∠2相等的条件;
D.利用等角的补角相等即可得出答案.
【解答】解:A.∵∠ADF+∠1=180°,∠1=∠2,
∴∠ADF+∠2=180°,故本选项不符合题意;
B.∵CD⊥EF,
∴∠BDC+∠2=90°,
∵∠1=∠2,
∴∠BDC+∠1=90°,故本选项不符合题意;
C.∠ADB≠∠2,故本选项符合题意;
D..∵CD⊥EF,
∴∠BDC+∠2=90°,
同理可得∠ADC+∠1=90°,
∵∠1=∠2,
∴∠BDC=∠ADC,
∴CD平分∠ABD,故本选项不符合题意;
故选:C.
【点评】本题主要考查余角和补角以及垂线的定义,解决此题的关键是熟练掌握这些知识点并灵活运用.
3.【答案】A
【分析】根据平行线的性质可得∠ABC=∠D=45°,再根据三角形内角与外角的关系可得∠1的度数.
【解答】解:如图,∵AB∥DE,
∴∠ABC=∠D=45°,
又∵∠A=30°,
∴∠1=∠A+∠ABC=75°,
故选:A.
【点评】此题主要考查了平行线的性质以及三角形外角性质的应用,关键是掌握两直线平行,同位角相等.
4.【答案】A
【分析】根据平行线的性质判断即可.
【解答】解:∵AD∥BC,
∴∠2=∠3,
故选:A.
【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.
5.【答案】D
【分析】先根据互为余角的定义求出∠BOD的度数,再分两种情况讨论:当∠BOD在直线AB上方时;当∠BOD在直线AB下方时;分别计算即可.
【解答】解:∵∠AOC=40°,∠BOD与∠AOC互余,
∴∠BOD=90°﹣∠AOC=90°﹣40°=50°,
当∠BOD在直线AB上方时,
∠DOC=180°﹣∠BOD﹣∠AOC=180°﹣50°﹣40°=90°;
当∠BOD在直线AB下方时,
∠AOD=180°﹣∠BOD=180°﹣50°=130°,
∴∠DOC=∠AOD+∠AOC=130°+40°=170°;
综上,∠DOC的度数为90°或170°,
故选:D.
【点评】本题考查了余角和补角,角的和差,注意分类讨论思想的运用.
6.【答案】D
【分析】根据平行线的性质可得∠1=∠2,根据∠1=53°解答即可.
【解答】解:∵a∥b,
∴∠1=∠2,
∵∠1=53°,
∴∠2=53°.
故选:D.
【点评】本题考查的是平行线的性质,解题的关键是熟练掌握平行线的性质并灵活运用;平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.
7.【答案】D
【分析】根据邻补角的概念求出∠AOD,根据角平分线的定义求出∠DOE,再根据邻补角的概念计算,得到答案.
【解答】解:∵∠1=36°,
∴∠AOD=180°﹣∠1=144°,
∵OE平分∠AOD,
∴∠DOE∠AOD=72°,
∴∠COE=180°﹣∠DOE=108°,
故选:D.
【点评】本题考查的是邻补角的概念、角平分线的定义,掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解题的关键.
8.【答案】A
【分析】由∠AOC=∠AOB﹣∠BOC,求出∠AOC,再由∠COD=∠AOD﹣∠AOC,即可计算.
【解答】解:∵∠AOC=∠AOB﹣∠BOC,
∴∠AOC=160°﹣90°=70°,
∵∠COD=∠AOD﹣∠AOC,
∴∠COD=90°﹣70°=20°.
故选:A.
【点评】本题考查角的计算,关键是由角的和差表示出有关的角即可.
9.【答案】D
【分析】由角平分线定义得到∠BAE=∠DAE,由平行线的性质推出∠EAB=∠F,∠DAE=∠AEB,由对顶角的性质得到∠CEF=∠AEB,即可得到答案.
【解答】解:∵AF平分∠DAB,
∴∠BAE=∠DAE,
∵AB∥CD,
∴∠EAB=∠F,
∵AD∥BC,
∴∠DAE=∠AEB,
∵∠CEF=∠AEB,
∴与∠EAB相等的角是∠DAE、∠F,∠AEB、∠CEF,个数是4个.
故选:D.
【点评】本题考查平行线是性质,关键是由平行线的性质推出∠EAB=∠F,∠DAE=∠AEB.
10.【答案】A
【分析】根据余角的定义进行计算即可.
【解答】解:∵∠α=70°,
∴∠α的余角的度数是:90°﹣70°=20°,
故选:A.
【点评】本题考查了余角的定义,两角之和等于90°,则这两个角互为余角.
二.填空题(共6小题)
11.【答案】51°32′.
【分析】根据余角的定义列式计算即可.
【解答】解:∵∠A=38°28′,
∴其余角为:90°﹣38°28′=51°32′,
故答案为:51°32′.
【点评】本题主要考查余角的定义,此定义是基础且重要知识点,必须掌握.
12.【答案】54°.
【分析】先求出∠DOC,再求出∠BOC.
【解答】解:∵∠AOC=90°,∠AOD=126°,
∴∠DOC=∠AOD﹣∠AOC=126°﹣90°=36°,
∵∠BOD=90°,
∴∠BOC=∠BOD﹣∠COD=90°﹣36°=54°.
故答案为:54°.
【点评】本题主要考查角的和差和余角的性质,解决本题的关键是找出互余的角.
13.【答案】39°50'.
【分析】用90°减去∠α的度数,即可求出它的余角的度数.
【解答】解:∵∠α=50°10',
∴它的余角=90°﹣50°10'=39°50'.
故答案为:39°50'.
【点评】本题主要考查余角的意义和度分秒的换算,熟练掌握求一个角的余角的方法是解决问题的关键.
14.【答案】0.5或1.5或3.5或4.5或5.
【分析】需要分类讨论,当DE∥AB时,BD∥AC时,当DE∥AC时,当BE∥AC时,当DE∥BC时,分别画出图形,根据平行线的性质求解即可.
【解答】解:当DE∥AB时,如图1,
此时∠ABE=∠E=30°,
∴∠CBE=15°,
t=15°÷30°=0.5;
当BD∥AC时,如图2,
此时∠DBC=45°,
t=45°÷30°=1.5;
当DE∥AC时,如图3,
此时,∠EBC=60°+45°=105°,
t=105°÷30°=3.5;
当BE∥AC时,如图4,
此时∠EBC=90°+45°=135°,
∴t=135°÷30°=4.5;
当DE∥BC时,如图5,
此时∠EBC=90°+60°=150°,
t=150°÷30°=5,
故答案为:0.5或1.5或3.5或4.5或5.
【点评】本题主要考查平行线的性质,分类讨论思想和数形结合思想,根据题意进行正确的分类讨论并作出图形是解题关键.
15.【答案】两直线平行,内错角相等.
【分析】根据平行线的性质得出∠AOB=∠MCO=7.2°,即可得到答案.
【解答】解:∵太阳光线是平行光线,
∴AO∥CM,
∴∠AOB=∠MCO=7.2°,
∴用到的原理是两直线平行,内错角相等.
故答案为:两直线平行,内错角相等.
【点评】本题主要考查了平行线的性质,掌握平行线的性质是解题关键.
16.【答案】∠ACD=90°(答案不唯一).
【分析】由平行线的判定,即可得到答案.
【解答】解:∵AB⊥AC,
∴∠BAC=90°,
若∠ACD=90°,则∠BAC=∠ACD,
∴AB∥CD,
∴要使AB∥CD,可添加∠ACD=90°(答案不唯一).
故答案为:∠ACD=90°(答案不唯一).
【点评】本题考查平行线的判定,关键是掌握平行线的判定方法.
三.解答题(共8小题)
17.【答案】(1)∠EOF=55°.
(2)①∠EOF=56°.
②k时,定值为2.
【分析】(1)由平分线得∠BOF=∠COF=α,∠COE=∠AOE=35°,由∠AOC与∠AOB互补得70°+70°+2α=180°,再计算即可.
(2)①设∠COD=2m,所以∠AOC=32°+6m,由角平分线得∠COE=∠EOA=16°+3m,∠BOF=∠COF=n,再计算即可.
②∠EOA=x+y,由角平分线得∠BOD=∠AOD,故2n+x=2y+x,所以n=y.化简得当2k﹣1=0时,即k时,原式为定值,再计算即可.
【解答】解:(1)∵OF平分∠BOC,
∴∠BOF=∠COF=α.
∵OE平分∠AOC,
∴∠COE=∠AOE=35°,
∵∠AOC与∠AOB互补,
∴70°+70°+2α=180°,
∴α=20°,
∴∠EOF=35°+20°=55°.
(2)①设∠COD=2m,
∵∠AOC﹣3∠COD=32°,
∴∠AOC=32°+6m,
∵OE平分∠AOC,
∴∠COE=∠EOA=16°+3m,
∴∠DOE=16°+3m﹣2m=16°+m.
∵OF平分∠BOC,
∴∠BOF=∠COF=n.
∵∠AOC与∠AOB互补,
∴32°+6m+32°+6m+2n=180°,
∴6m+n=58°①.
∵OD平分∠AOB,
∴∠BOD=∠AOD,
∴2n+2m=16°+m+16°+3m,
∴n﹣m=16°②,
由①②得m=6°,n=22°,
∴∠EOF=n+16+3m=56°.
②当k=时,的值时一个定值.
理由如下:
∴∠EOA=x+y,
∵OD平分∠AOB,
∴∠BOD=∠AOD,
∴2n+x=2y+x,
∴n=y.
∴
当2k﹣1=0时,即k时,
原式
=2.
答:k时,定值为2.
【点评】本题考查了余角和补角的知识,看图表示出角的度数是解题关键.
18.【答案】(1)56°;
(2)80°.
【分析】(1)根据已知条件得到∠BOF=∠DOF﹣∠BOD=90°﹣68°=22°,角平分线得到,再根据∠EOF=∠BOF+∠BOE,即可得解;
(2)角平分线和平角得到,再根据角平分线,得到,再利用∠BOF=∠EOF﹣∠BOE,进行计算即可.
【解答】解:(1)∵∠DOF=90°,∠BOD=68°,
∴∠BOF=∠DOF﹣∠BOD=90°﹣68°=22°,
∵OE平分∠BOD,
∴,
∴∠EOF=∠BOF+∠BOE=22°+34°=56°;
(2)∵OE平分∠BOD,
∴,
∴,
∵OF平分∠COE,
∴
,
∵∠BOF=∠EOF﹣∠BOE,
∴,
∴∠BOD=80°.
【点评】本题考查几何图形中角度的计算.正确的识图,理清角度之间的和差,倍数关系,是解题的关键.
19.【答案】(1)38°或64;
(2)∠BOD=30°;
(3)∠EOF=2∠DOG或∠EOF+∠DOG=45°.
【分析】(1)分两种情况,即当∠DOE+∠AOD=180°和∠AOE+∠AOD=180°时,分别画出相应的图形,由角平分线的定义以及图形中角的和差关系进行解答即可;
(2)根据平角的定义以及角平分线的定义进行计算即可;
(3)分(1)中的两种情况进行解答,分别用∠BOD表示∠EOF,∠DOG,进而答案即可.
【解答】解:(1)如图1﹣1,由于射线OE是∠AOD的“好线”,
当∠DOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠DOE=∠BOD=26°,
∵OC⊥OD,
∴∠COD=90°,
∴∠COE=90°﹣26°=64°,
如图1﹣2,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠AOE=∠BOD=26°,
∴∠COE=180°﹣26°﹣26°﹣90°=38°,
因此∠COE=38°或∠COE=64°,
故答案为:38°或64;
(2)若OE恰好平分∠AOC,
∴∠AOE=∠COE=∠BOD,
∴∠BOD(180°﹣90°)=30°;
(3)∠EOF=2∠DOG或∠EOF+∠DOG=45°,理由如下:
如图2﹣1,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠BOD=180°,
∴∠AOE=∠BOD,
∵OF是∠AOE的平分线,
∴∠EOF∠AOE∠BOD,
∴OG是∠BOC的平分线,
∴∠BOG∠BOC(90°+∠BOD)=45°∠BOD,
∴∠DOG=∠BOG﹣∠BOD=45°∠BOD,
∴∠EOF+∠DOG=45°,
如图2﹣2,由于射线OE是∠AOD的“好线”,
当∠AOE+∠AOD=180°时,
∵∠AOD+∠EOD=180°,
∴∠DOE=∠BOD,
∴∠DOG∠BOC﹣∠BOD
(90°+∠BOD)﹣∠BOD
=45°∠BOD,
∠EOF∠AOE(180°﹣2∠BOD)
=90°﹣∠BOD,
∴∠EOF=2∠DOG,
综上所述∠EOF=2∠DOG或∠EOF+∠DOG=45°.
【点评】本题考查角平分线,余角与补角,掌握角平分线的定义,余角与补角的定义,理解“好线”的定义是正确解答的关键.
20.【答案】(1)45°;(2)60°;(3).
【分析】(1)求得∠AOC+∠BOD=90°,利用角平分线的定义得,据此求解即可;
(2)求得∠AOC+∠BOD=120°,利用角平分线的定义得,据此求解即可;
(3)求得∠AOC+∠BOD=180°﹣α,利用角平分线的定义得求解即可.
【解答】解:(1)因为∠COD=90°,所以∠AOC+∠BOD=90°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
故答案为:45°;
(2)因为∠COD=60°,所以∠AOC+∠BOD=120°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
(3)因为∠COD=α,所以∠AOC+∠BOD=180°﹣α,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
.
【点评】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
21.【答案】(1)30°.
(2)∠BOC﹣∠AOD=30°,或∠BOC+∠AOD=30°,或∠AOD﹣∠BOC=30°.
(3)25分钟时,OD边第一次与OB边重合.
【分析】(1)由∠BOC=∠BOA﹣∠COA,∠AOD=∠COD﹣∠COA,得∠BOC﹣∠AOD=(∠BOA﹣∠COA)﹣(∠COD﹣∠COA)=∠BOA﹣∠COD=90°﹣60°=30°.
(2)设∠COA=α,分三种情况讨论:①当0°<α≤60°时,②当60°<α≤90°时,③当90°<α≤180°时,把∠BOC和∠AOD用含α的式子表示,再计算即可.
(3)先求出OD按每分钟15°的速度旋转,OB按每分钟9°的速度,再按照追击问题得150÷(15﹣9)=25(分钟).
【解答】解:(1)∵∠BOC=∠BOA﹣∠COA,
又∠AOD=∠COD﹣∠COA,
∴∠BOC﹣∠AOD=(∠BOA﹣∠COA)﹣(∠COD﹣∠COA)=∠BOA﹣∠COD=90°﹣60°=30°.
故答案为:30°.
(2)设∠COA=α,
①当0°<α≤60°时,如图a,由(1)得∴∠BOC﹣∠AOD=30°.
②当60°<α≤90°时,如图b,
∠BOC=90°﹣α,∠AOD=α﹣60°,
∴∠BOC+∠AOD=90°﹣α+α﹣60°=30°.
③当90°<α≤180°时,如图c,
∠BOC=60°﹣α,∠AOD=90°﹣α,
∴∠AOD﹣∠BOC=90°﹣α﹣(60°﹣α)=30°.
综上所述,∠BOC﹣∠AOD=30°,或∠BOC+∠AOD=30°,或∠AOD﹣∠BOC=30°.
(3)∵△COD按每分钟15°的速度旋转,
∴OD按每分钟15°的速度旋转,
同理,OB按每分钟9°的速度,
∵∠BOD=∠BOA+∠AOD=90°+60°=150°,
∴150÷(15﹣9)=25(分钟).
答:25分钟时,OD边第一次与OB边重合.
【点评】本题考查了余角和补角的知识,利用数形结合,列出算式计算是解题关键.
22.【答案】这个角的度数是60°.
【分析】设这个角为x,则余角为90°﹣x,补角为180°﹣x,根据题意表述可列出方程,解出即可.
【解答】解:设这个角为x,则余角为90°﹣x,补角为180°﹣x,
由题意得:90°﹣x(180°﹣x)﹣50°,
解得:x=60°.
∴这个角的度数是60°.
【点评】本题考查在余角和补角的知识基础上,考查一元一次方程的应用,难度不大,关键是运用方程思想解题.
23.【答案】见试题解答内容
【分析】(1)当∠DCE=30°时,利用互余计算出∠BCD,然后可得到∠ACB+∠DCE的度数;若∠DCE为任意锐角时,利用∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,然后计算出∠ACB+∠DCE=180°;
(2)利用周角定义得到∠ACD+∠ECB+∠ACB+∠DCE=360°所以∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=180°.
【解答】解:(1)∠ACB+∠DCE=180°;
若∠DCE为任意锐角时,∠ACB+∠DCE=180°,
理由如下:∵∠ACE+∠DCE=90°,
∠BCD+∠DCE=90°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°;
(2)∠ACB+∠DCE=180°.
理由如下:∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°.
故答案为30°.
【点评】本题考查了余角和补角:等角的补角相等.等角的余角相等;余角和补角计算的应用,常常与等式的性质、等量代换相关联.
24.【答案】(1)∠MON=70°;
(2)∠MON∠AOB;
(3)∠MON=110°.
【分析】(1)已知∠AOB=140°,射线OC是∠AOB内部任意一条射线,可得∠AOC+∠BOC的度数,因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON的度数,即∠MON的度数;
(2)因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)∠AOB,即∠MON∠AOB;
(3)已知∠AOB=140°,射线OC是∠AOB外部任意一条射线,可得∠AOC+∠BOC的度数,因为射线OM、ON分别平分∠AOC、∠BOC,所以∠COM+∠CON的度数,即∠MON的度数.
【解答】解:(1)∵∠AOB=140°,射线OC是∠AOB内部任意一条射线,
∴∠AOC+∠BOC=140°,
又∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)=70°,
∴∠MON=70°;
(2)∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)∠AOB,
∴∠MON∠AOB,
故答案为:∠MON∠AOB;
(3)∵∠AOB=140°,射线OC是∠AOB外部任意一条射线,
∴∠AOC+∠BOC=220°,
又∵射线OM、ON分别平分∠AOC、∠BOC,
∴∠COM+∠CON∠AOC∠BOC(∠AOC+∠BOC)=110°,
∴∠MON=110°.
【点评】本题考查了角平分线,关键是掌握角平分线的定义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
