第二章 二次函数 达标测试卷(含答案) 2025-2026学年数学北师大版(2024)九年级下册
文档属性
| 名称 | 第二章 二次函数 达标测试卷(含答案) 2025-2026学年数学北师大版(2024)九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 21:39:42 | ||
图片预览


文档简介
第二章《二次函数》达标测试卷
第一部分 选择题
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列y关于x的函数中,是二次函数的是( )
A.y=3x+1 B.y= C.y= D.y=2x2+1
2.抛物线y=-(x+1)2-1的顶点坐标是( )
A.(-1,-1) B.(1,-1) C.(-1,1) D.(1,1)
3.已知顶点为(2,4)的抛物线过点(4,0),此抛物线的表达式是( )
A.y=-(x-2)2+4 B.y=(x-2)2-4
C.y=(x-2)2+4 D.y=-(x-2)2-4
4.将抛物线y=x2+1先向上平移2个单位长度,再向右平移3个单位长度,所得新抛物线的表达式为( )
A.y=(x+3)2+3 B.y=(x-3)2-1
C.y=(x+3)2-1 D.y=(x-3)2+3
5.如图,抛物线y=ax2+bx+c的一部分经过点A(-1,0),且其对称轴是直线x=2,则一元二次方程ax2+bx+c=0的根是( )
第5题图
A.x1=-1 B.x1=-1,x2=5C.x1=-1,x2=3 D.x1=-1,x2=1
6.把二次函数y=x2-6x-1化成y=a(x-h)2+k的形式是( )
A.y=(x+3)2-10 B.y=(x+3)2+8 C.y=(x-3)2-10 D.y=(x-3)2+8
7.函数y=ax2-2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
8.如图所示是二次函数y=ax2+bx+c(a≠0)的部分图象,该函数图象的对称轴是直线x=1,图象与y轴交点的纵坐标是2,则下列结论:①2a+b=0;②方程ax2+bx+c=0一定有一个根在-2和-1之间;③方程ax2+bx+c-=0一定有两个不相等的实数根;④b-a<2.其中,正确的结论有( )
第8题图
A.1个 B.2个 C.3个 D.4个
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
9.二次函数y=2x2-x-3的图象的对称轴为直线 .
10.若y=(m-3)+2x+1是关于x的二次函数,则m的值为 .
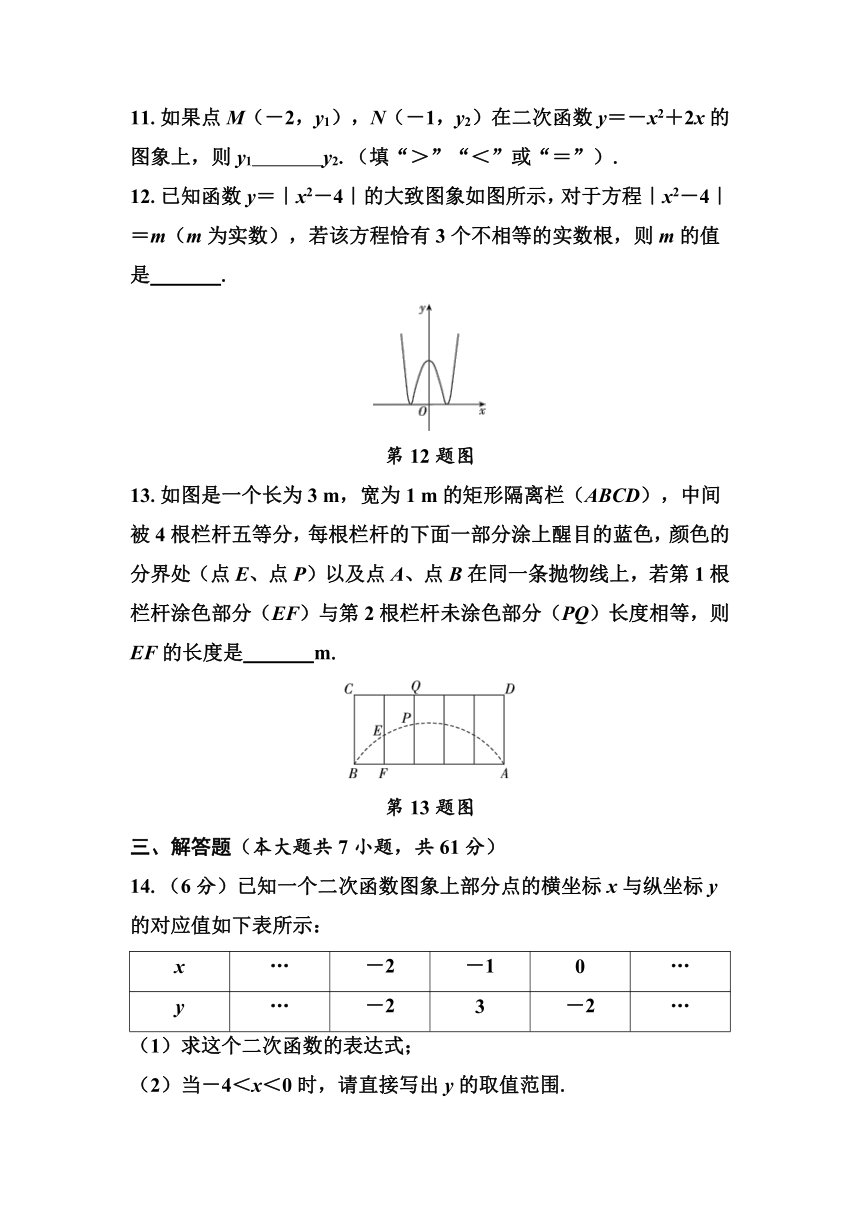
11.如果点M(-2,y1),N(-1,y2)在二次函数y=-x2+2x的图象上,则y1 y2.(填“>”“<”或“=”).
12.已知函数y=|x2-4|的大致图象如图所示,对于方程|x2-4|=m(m为实数),若该方程恰有3个不相等的实数根,则m的值是 .
第12题图
13.如图是一个长为3 m,宽为1 m的矩形隔离栏(ABCD),中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E、点P)以及点A、点B在同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是 m.
第13题图
三、解答题(本大题共7小题,共61分)
14.(6分)已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x … -2 -1 0 …
y … -2 3 -2 …
(1)求这个二次函数的表达式;
(2)当-4<x<0时,请直接写出y的取值范围.
15.(6分)已知二次函数y=x2+3mx-1-m的图象与x轴的一个交点为(3,0).
(1)求m的值;
(2)求这个函数图象与x轴另一个交点的横坐标.
16.(8分)新华书店购进一批建国70周年纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为23元时,销售量为34本;当销售单价为25元时,销售量为30本.
(1)求出y与x的函数关系式;
(2)设书店每周销售这种纪念册所获得的利润为w元,将销售单价定为多少元时,每周所获利润最大?最大利润是多少?
17.(8分)如图,在△ABC中,BC=6 cm,AC=8 cm,AB=10 cm,P点在BC上从B点运动到C点(不包括C点),点P运动的速度为1 cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2 cm/s.若点P,Q分别从B,C同时运动,请解答下面的问题,并写出探索的主要过程:
(1)经过多少时间后,P,Q两点的距离最短,最短距离是多少?
(2)经过多少时间后,△PCQ的面积最大,最大面积是多少?
18.(9分)如图,二次函数y=-x2+6x-5a的图象交x轴正半轴于A,B两点(点A在点B的左边),交y轴于点C,连接AC,BC,已知OC=5.
(1)求二次函数的表达式;
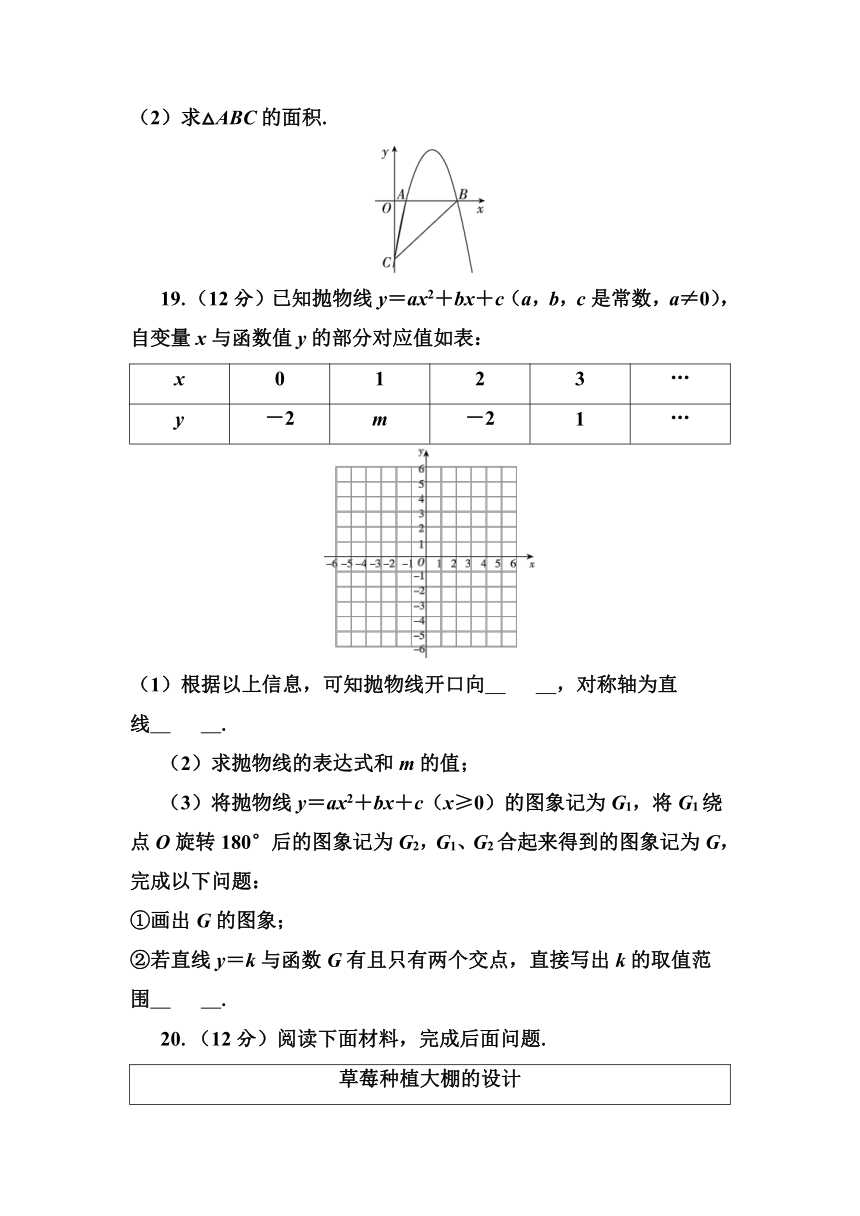
(2)求△ABC的面积.
19.(12分)已知抛物线y=ax2+bx+c(a,b,c是常数,a≠0),自变量x与函数值y的部分对应值如表:
x 0 1 2 3 …
y -2 m -2 1 …
(1)根据以上信息,可知抛物线开口向 ,对称轴为直线 .
(2)求抛物线的表达式和m的值;
(3)将抛物线y=ax2+bx+c(x≥0)的图象记为G1,将G1绕点O旋转180°后的图象记为G2,G1、G2合起来得到的图象记为G,完成以下问题:
①画出G的图象;
②若直线y=k与函数G有且只有两个交点,直接写出k的取值范围 .
20.(12分)阅读下面材料,完成后面问题.
草莓种植大棚的设计
生活背景 草莓种植大棚是一种具有保温性能的框架结构,如图所示,一般使用钢结构作为骨架,上面覆上一层或多层塑料膜,这样就形成了一个温室空间.大棚的设计要保证通风性且利于采光.
建立模型 如图1,已知某草莓园的种植大棚横截面可以看作抛物线OPN,其中点P为抛物线的顶点,大棚高PE=4 m,宽ON=12 m.现以点O为坐标原点,ON所在直线为x轴,过点O且垂直于ON的直线为y轴建立平面直角坐标系.
解决问题 (1)求抛物线的表达式. (2)如图2,为方便进出,在大棚横截面中间开了两扇正方形的门,其中AB=BE=EC=CD.求门高AB的值. (3)若在某一时刻,太阳光线(假设太阳光线为平行线)透过A点恰好照射到N点,此时大棚横截面在地面上的阴影为线段OQ,求此时OQ的长.
参考答案
1.D 2.A 3.A 4.D 5.B 6.C 7.A
8.B 解析:如图,
∵抛物线的对称轴为直线x=1,
∴-=1,
∴b=-2a,
∴2a+b=0,故①正确;
∵抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点在2和3之间,
∴与x轴的另一个交点在-1和0之间,
∴方程ax2+bx+c=0一定有一个根在-1和0之间,故②错误;
∵抛物线y=ax2+bx+c与直线y=有两个交点,
∴方程ax2+bx+c-=0一定有两个不相等的实数根,故③正确;
∵抛物线与x轴的另一个交点在-1和0之间,
∴a-b+c<0.
∵图象与y轴交点的纵坐标是2,
∴c=2,
∴a-b+2<0,
∴b-a>2,故④错误.故选B.
9.x= 10.-1 11.< 12.4 13.
14.解:(1)设这个二次函数的表达式为y=ax2+bx+c.
根据题意,得解得
故这个二次函数的表达式为y=-5x2-10x-2.
(2)∵y=-5x2-10x-2=-5(x+1)2+3,
∴对称轴x=-1在-4<x<0中,在对称轴的左侧,y随x的增大而增大,
当x=-4时,y=-5x2-10x-2=-42,
当x=-1时,y=3,当x=0时,y=-2,
故y的取值范围为-42<y≤3.
15.解:(1)将坐标(3,0)代入函数y=x2+3mx-1-m,得9+9m-1-m=0,
∴m=-1.
(2)由(1)可得二次函数为y=x2-3x.
令y=0,则x2-3x=0.∴x=3或x=0.
∵抛物线与x轴的一个交点为(3,0),
∴这个函数图象与x轴另一个交点的横坐标为0.
16.解:(1)设y与x的函数关系式为y=kx+b.
把坐标(23,34)与(25,30)分别代入,得解得
∴所求函数关系式为y=-2x+80.
(2)由题意可得w=(x-20)(-2x+80)=-2x2+120x-1 600=-2(x-30)2+200,
当x=30时,w最大,w最大=-2×(30-30)2+200=200(元).
答:当销售单价定为30元时,每周所获利润最大,最大利润是200元.
17.解:(1)由题意可得BP=t cm,CP=(6-t) cm,CQ=2t cm,
∴PQ===,
当t=时,PQ最小,最小值为 cm.
答:经过 s后,P,Q两点的距离最短,最短距离是 cm.
(2)S=(6-t)×2t÷2=-t2+6t=-(t-3)2+9,
当t=3时,面积最大,最大面积为9 cm2.
18.解:(1)由题意,令x=0,
∴y=-5a.
又OC=5,
∴-5a=-5.∴a=1.
∴二次函数的表达式为y=-x2+6x-5.
(2)由(1)得抛物线为y=-x2+6x-5.
∴令y=0,则0=-x2+6x-5.∴x=1或x=5.∴AB=5-1=4.
又OC=5,
∴S△ABC=AB·OC=×4×5=10.
19.解:(1)根据表格数据可知,其对称轴为直线x=1,在对称轴的右侧y随x的增大而增大,
∴抛物线开口向上.故答案为上;x=1.
解:(2)由(1)得,对称轴为直线x=1,根据表格数据可知顶点坐标为(1,m),
∴设抛物线的表达式为y=a(x-1)2+m,且过(0,-2),(3,1),
∴解得
∴抛物线的表达式为y=(x-1)2-3或y=x2-2x-2.
解:(3)①由(2)得,抛物线的表达式为y=(x-1)2-3,
∴顶点坐标为(1,-3),则绕点O旋转180°后的图象G2为y=-(x+1)2+3,
根据画函数图象的方法,如图.
②根据图象可知,直线y=k与函数G有且只有两个交点时,
k的取值范围为k=3或k=-3或-2<k<2,
故答案为k=-3或k=3或-2<k<2.
20.解:(1)由题意得,抛物线的顶点为(6,4),
∴可设抛物线的表达式为y=a(x-6)2+4.
又抛物线过(0,0),
∴0=36a+4,
∴a=-.
∴抛物线的表达式为y=-(x-6)2+4,
(2)由题意,设AB=BE=EC=CD=m,
∴A(6-m,m).
又A在抛物线y=-(x-6)2+4上,
∴m=-m2+4.
∴m=3或m=-12(舍去).∴AB=3.
答:门高AB为3 m.
(3)由上面的计算知A(3,3),N(12,0),
∴直线AN为y=-x+4.
∵PQ∥AN,
∴可设PQ为y=-x+b,
∴-(x-6)2+4=-x+b.
∴x2-15x+9b=0.∴Δ=225-36b=0.
∴b=.∴直线PQ为y=-x+.
令y=0,得x=,即OQ= m.
答:此时OQ的长为 m.
第一部分 选择题
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列y关于x的函数中,是二次函数的是( )
A.y=3x+1 B.y= C.y= D.y=2x2+1
2.抛物线y=-(x+1)2-1的顶点坐标是( )
A.(-1,-1) B.(1,-1) C.(-1,1) D.(1,1)
3.已知顶点为(2,4)的抛物线过点(4,0),此抛物线的表达式是( )
A.y=-(x-2)2+4 B.y=(x-2)2-4
C.y=(x-2)2+4 D.y=-(x-2)2-4
4.将抛物线y=x2+1先向上平移2个单位长度,再向右平移3个单位长度,所得新抛物线的表达式为( )
A.y=(x+3)2+3 B.y=(x-3)2-1
C.y=(x+3)2-1 D.y=(x-3)2+3
5.如图,抛物线y=ax2+bx+c的一部分经过点A(-1,0),且其对称轴是直线x=2,则一元二次方程ax2+bx+c=0的根是( )
第5题图
A.x1=-1 B.x1=-1,x2=5C.x1=-1,x2=3 D.x1=-1,x2=1
6.把二次函数y=x2-6x-1化成y=a(x-h)2+k的形式是( )
A.y=(x+3)2-10 B.y=(x+3)2+8 C.y=(x-3)2-10 D.y=(x-3)2+8
7.函数y=ax2-2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
8.如图所示是二次函数y=ax2+bx+c(a≠0)的部分图象,该函数图象的对称轴是直线x=1,图象与y轴交点的纵坐标是2,则下列结论:①2a+b=0;②方程ax2+bx+c=0一定有一个根在-2和-1之间;③方程ax2+bx+c-=0一定有两个不相等的实数根;④b-a<2.其中,正确的结论有( )
第8题图
A.1个 B.2个 C.3个 D.4个
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
9.二次函数y=2x2-x-3的图象的对称轴为直线 .
10.若y=(m-3)+2x+1是关于x的二次函数,则m的值为 .
11.如果点M(-2,y1),N(-1,y2)在二次函数y=-x2+2x的图象上,则y1 y2.(填“>”“<”或“=”).
12.已知函数y=|x2-4|的大致图象如图所示,对于方程|x2-4|=m(m为实数),若该方程恰有3个不相等的实数根,则m的值是 .
第12题图
13.如图是一个长为3 m,宽为1 m的矩形隔离栏(ABCD),中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E、点P)以及点A、点B在同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是 m.
第13题图
三、解答题(本大题共7小题,共61分)
14.(6分)已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x … -2 -1 0 …
y … -2 3 -2 …
(1)求这个二次函数的表达式;
(2)当-4<x<0时,请直接写出y的取值范围.
15.(6分)已知二次函数y=x2+3mx-1-m的图象与x轴的一个交点为(3,0).
(1)求m的值;
(2)求这个函数图象与x轴另一个交点的横坐标.
16.(8分)新华书店购进一批建国70周年纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为23元时,销售量为34本;当销售单价为25元时,销售量为30本.
(1)求出y与x的函数关系式;
(2)设书店每周销售这种纪念册所获得的利润为w元,将销售单价定为多少元时,每周所获利润最大?最大利润是多少?
17.(8分)如图,在△ABC中,BC=6 cm,AC=8 cm,AB=10 cm,P点在BC上从B点运动到C点(不包括C点),点P运动的速度为1 cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2 cm/s.若点P,Q分别从B,C同时运动,请解答下面的问题,并写出探索的主要过程:
(1)经过多少时间后,P,Q两点的距离最短,最短距离是多少?
(2)经过多少时间后,△PCQ的面积最大,最大面积是多少?
18.(9分)如图,二次函数y=-x2+6x-5a的图象交x轴正半轴于A,B两点(点A在点B的左边),交y轴于点C,连接AC,BC,已知OC=5.
(1)求二次函数的表达式;
(2)求△ABC的面积.
19.(12分)已知抛物线y=ax2+bx+c(a,b,c是常数,a≠0),自变量x与函数值y的部分对应值如表:
x 0 1 2 3 …
y -2 m -2 1 …
(1)根据以上信息,可知抛物线开口向 ,对称轴为直线 .
(2)求抛物线的表达式和m的值;
(3)将抛物线y=ax2+bx+c(x≥0)的图象记为G1,将G1绕点O旋转180°后的图象记为G2,G1、G2合起来得到的图象记为G,完成以下问题:
①画出G的图象;
②若直线y=k与函数G有且只有两个交点,直接写出k的取值范围 .
20.(12分)阅读下面材料,完成后面问题.
草莓种植大棚的设计
生活背景 草莓种植大棚是一种具有保温性能的框架结构,如图所示,一般使用钢结构作为骨架,上面覆上一层或多层塑料膜,这样就形成了一个温室空间.大棚的设计要保证通风性且利于采光.
建立模型 如图1,已知某草莓园的种植大棚横截面可以看作抛物线OPN,其中点P为抛物线的顶点,大棚高PE=4 m,宽ON=12 m.现以点O为坐标原点,ON所在直线为x轴,过点O且垂直于ON的直线为y轴建立平面直角坐标系.
解决问题 (1)求抛物线的表达式. (2)如图2,为方便进出,在大棚横截面中间开了两扇正方形的门,其中AB=BE=EC=CD.求门高AB的值. (3)若在某一时刻,太阳光线(假设太阳光线为平行线)透过A点恰好照射到N点,此时大棚横截面在地面上的阴影为线段OQ,求此时OQ的长.
参考答案
1.D 2.A 3.A 4.D 5.B 6.C 7.A
8.B 解析:如图,
∵抛物线的对称轴为直线x=1,
∴-=1,
∴b=-2a,
∴2a+b=0,故①正确;
∵抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点在2和3之间,
∴与x轴的另一个交点在-1和0之间,
∴方程ax2+bx+c=0一定有一个根在-1和0之间,故②错误;
∵抛物线y=ax2+bx+c与直线y=有两个交点,
∴方程ax2+bx+c-=0一定有两个不相等的实数根,故③正确;
∵抛物线与x轴的另一个交点在-1和0之间,
∴a-b+c<0.
∵图象与y轴交点的纵坐标是2,
∴c=2,
∴a-b+2<0,
∴b-a>2,故④错误.故选B.
9.x= 10.-1 11.< 12.4 13.
14.解:(1)设这个二次函数的表达式为y=ax2+bx+c.
根据题意,得解得
故这个二次函数的表达式为y=-5x2-10x-2.
(2)∵y=-5x2-10x-2=-5(x+1)2+3,
∴对称轴x=-1在-4<x<0中,在对称轴的左侧,y随x的增大而增大,
当x=-4时,y=-5x2-10x-2=-42,
当x=-1时,y=3,当x=0时,y=-2,
故y的取值范围为-42<y≤3.
15.解:(1)将坐标(3,0)代入函数y=x2+3mx-1-m,得9+9m-1-m=0,
∴m=-1.
(2)由(1)可得二次函数为y=x2-3x.
令y=0,则x2-3x=0.∴x=3或x=0.
∵抛物线与x轴的一个交点为(3,0),
∴这个函数图象与x轴另一个交点的横坐标为0.
16.解:(1)设y与x的函数关系式为y=kx+b.
把坐标(23,34)与(25,30)分别代入,得解得
∴所求函数关系式为y=-2x+80.
(2)由题意可得w=(x-20)(-2x+80)=-2x2+120x-1 600=-2(x-30)2+200,
当x=30时,w最大,w最大=-2×(30-30)2+200=200(元).
答:当销售单价定为30元时,每周所获利润最大,最大利润是200元.
17.解:(1)由题意可得BP=t cm,CP=(6-t) cm,CQ=2t cm,
∴PQ===,
当t=时,PQ最小,最小值为 cm.
答:经过 s后,P,Q两点的距离最短,最短距离是 cm.
(2)S=(6-t)×2t÷2=-t2+6t=-(t-3)2+9,
当t=3时,面积最大,最大面积为9 cm2.
18.解:(1)由题意,令x=0,
∴y=-5a.
又OC=5,
∴-5a=-5.∴a=1.
∴二次函数的表达式为y=-x2+6x-5.
(2)由(1)得抛物线为y=-x2+6x-5.
∴令y=0,则0=-x2+6x-5.∴x=1或x=5.∴AB=5-1=4.
又OC=5,
∴S△ABC=AB·OC=×4×5=10.
19.解:(1)根据表格数据可知,其对称轴为直线x=1,在对称轴的右侧y随x的增大而增大,
∴抛物线开口向上.故答案为上;x=1.
解:(2)由(1)得,对称轴为直线x=1,根据表格数据可知顶点坐标为(1,m),
∴设抛物线的表达式为y=a(x-1)2+m,且过(0,-2),(3,1),
∴解得
∴抛物线的表达式为y=(x-1)2-3或y=x2-2x-2.
解:(3)①由(2)得,抛物线的表达式为y=(x-1)2-3,
∴顶点坐标为(1,-3),则绕点O旋转180°后的图象G2为y=-(x+1)2+3,
根据画函数图象的方法,如图.
②根据图象可知,直线y=k与函数G有且只有两个交点时,
k的取值范围为k=3或k=-3或-2<k<2,
故答案为k=-3或k=3或-2<k<2.
20.解:(1)由题意得,抛物线的顶点为(6,4),
∴可设抛物线的表达式为y=a(x-6)2+4.
又抛物线过(0,0),
∴0=36a+4,
∴a=-.
∴抛物线的表达式为y=-(x-6)2+4,
(2)由题意,设AB=BE=EC=CD=m,
∴A(6-m,m).
又A在抛物线y=-(x-6)2+4上,
∴m=-m2+4.
∴m=3或m=-12(舍去).∴AB=3.
答:门高AB为3 m.
(3)由上面的计算知A(3,3),N(12,0),
∴直线AN为y=-x+4.
∵PQ∥AN,
∴可设PQ为y=-x+b,
∴-(x-6)2+4=-x+b.
∴x2-15x+9b=0.∴Δ=225-36b=0.
∴b=.∴直线PQ为y=-x+.
令y=0,得x=,即OQ= m.
答:此时OQ的长为 m.
