九年级下册期末达标测试卷 (含答案) 2025-2026学年数学北师大版(2024)
文档属性
| 名称 | 九年级下册期末达标测试卷 (含答案) 2025-2026学年数学北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-30 09:17:17 | ||
图片预览




文档简介
九下期末达标测试卷
第一部分 选择题
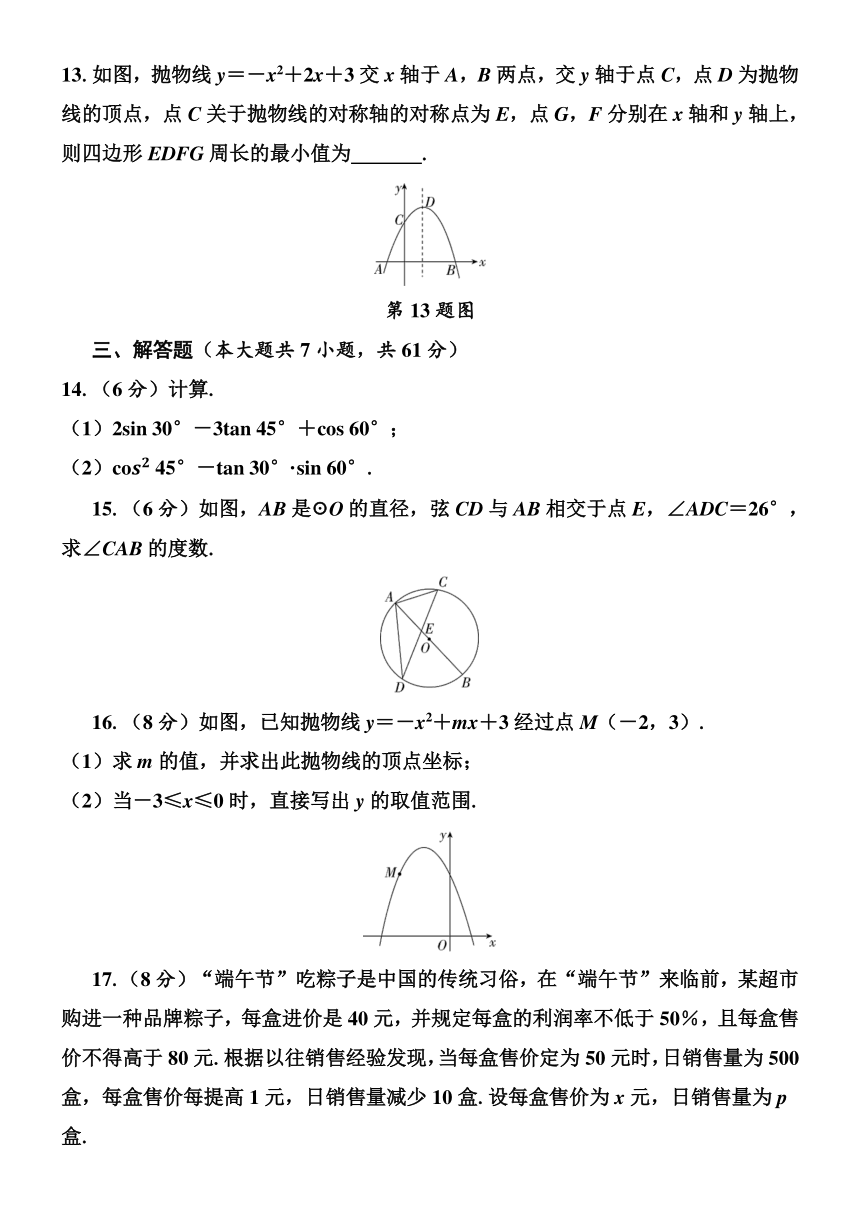
一、选择题(本大题共8小题,每小题3分,共24分)
1.计算sin 45°的值等于( )
A. B. C. D.
2.如图,AB是☉O的直径,C是☉O上一点.若∠BOC=66°,则∠A=( )
第2题图
A.66° B.33° C.24° D.30°
3.如图,某水库堤坝横断面迎水坡AB的坡角为α,堤坝高BC为50 m,则迎水坡面AB的长度是( )
第3题图
A.50·tan α m B.50·sin α m C. m D. m
4.如图,CD为☉O的直径,弦AB⊥CD于点E,CE=1,AB=6,则CD长为( )
第4题图
A.10 B.9 C.8 D.5
5.如图,二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B两点,对称轴是直线x=1,下列说法正确的是( )
第5题图
A.a>1 B.当x>-1时,y的值随x值的增大而增大
C.点B的坐标为(4,0) D.4a+2b+c>0
6.如图,☉C过原点O,且与两坐标轴分别交于A,B两点,点A的坐标为(0,5),点M是第三象限内上一点,∠BMO=120°,则☉O的半径为( )
第6题图
A.4 B.5 C.6 D.2
7.如图,客轮在海上以30 km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1 h后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是( )
第7题图
A. 15 km B. 15 km C. 15(+)km D.5(3+)km
8.苏州园林中的月亮门是中国古典园林住宅中常见的圆弧形洞门(如图1),因圆形如月而得名.月亮门因其寓意美好且造型独特,被广泛使用.图2是小明同学家中的月亮门示意图,经测量,水平跨径AB为2.4米,水平木条BD和铅锤木条CD长都为0.4米,点C恰好落在☉O上,则此月亮门的半径为( )
第8题图
A.2.1米 B.2.0米 C.1.9米 D.1.8米
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
9.如图,在△ABC中,∠ACB=90°,BC=12,AB=15,则cos B的值为 .
第9题图
10.请写出一个开口向上,经过点(0,4)的抛物线的表达式 .
11.如图,AD切☉O于A点,BC为直径,连接CA,已知∠ACB=20°,则∠CAD的度数为 .
第11题图
12.如图,在菱形ABCD中,分别以点A,C为圆心,AD,CB的长为半径画弧,分别交对角线AC于点E,F.若AB=4,∠ABC=120°,则图中阴影部分的面积为 .(结果保留π)
第12题图
13.如图,抛物线y=-x2+2x+3交x轴于A,B两点,交y轴于点C,点D为抛物线的顶点,点C关于抛物线的对称轴的对称点为E,点G,F分别在x轴和y轴上,则四边形EDFG周长的最小值为 .
第13题图
三、解答题(本大题共7小题,共61分)
14.(6分)计算.
(1)2sin 30°-3tan 45°+cos 60°;
(2)co45°-tan 30°·sin 60°.
15.(6分)如图,AB是☉O的直径,弦CD与AB相交于点E,∠ADC=26°,求∠CAB的度数.
16.(8分)如图,已知抛物线y=-x2+mx+3经过点M(-2,3).
(1)求m的值,并求出此抛物线的顶点坐标;
(2)当-3≤x≤0时,直接写出y的取值范围.
17.(8分)“端午节”吃粽子是中国的传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒的利润率不低于50%,且每盒售价不得高于80元.根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒.设每盒售价为x元,日销售量为p盒.
(1)当x=60时,p= ;
(2)当每盒售价定为多少元时,日销售额y(元)最大?最大日销售额是多少元?
18.(9分)如图,在△ABC中,∠C=90°,点E在AC边上,BE平分∠ABC,DE⊥BE交AB于点D,☉O是△BDE的外接圆.
(1)求证:AC是☉O的切线;
(2)若AD=2,AE=4,求☉O的半径长.
19.(12分)数形结合是解决数学问题的重要方法.小明同学学习二次函数后,对函数y=-(|x|-1)2进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:
【观察探究】
方程-(|x|-1)2=-1的解为 ;
【问题解决】
若方程-(|x|-1)2=a有四个实数根,分别为x1,x2,x3,x4.
①a的取值范围是 ;
②计算x1+x2+x3+x4= ;
【拓展延伸】
①将函数y=-(|x|-1)2的图象经过怎样的平移可得到函数y1=-(|x-2|-1)2+3的图象?画出平移后的图象并写出平移过程;
②观察平移后的图象,当2≤y1≤3时,直接写出自变量x的取值范围 .
20.(12分)蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它的出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图1,某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成,其中AB=3 m,BC=4 m,取BC的中点O,过点O作线段BC的垂直平分线OE交抛物线AED于点E,若以O点为原点,BC所在直线为x轴,OE为y轴建立如图所示平面直角坐标系.
请回答下列问题:
(1)如图2,抛物线AED的顶点E(0,4),求抛物线的表达式;
(2)如图3,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置LFGT,SMNR,若FL=NR=0.75 m,求两个正方形装置的间距GM的长;
(3)如图4,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为CK,求CK的长.
参考答案
1.C 2.B 3.D 4.A 5.D 6.B 7.D 8.B
9. 10.y=x2+4(答案不唯一) 11.70° 12.8-
13.+ 解析:如图,在y=-x2+2x+3中,当x=0时,y=3,即点C(0,3).
∵y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1,顶点D(1,4),
则点C关于对称轴的对称点E的坐标为(2,3).
作点D关于y轴的对称点D'(-1,4),作点E关于x轴的对称点E'(2,-3).
连接D'E',与x轴交于点G,与y轴交于点F,则点G,F即为使四边形EDFG的周长最小的点,四边形EDFG的周长=DE+DF+FG+GE=DE+D'F+FG+GE'=DE+D'E'
=+=+,
∴四边形EDFG的周长的最小值为+.
14.解:(1)2sin 30°-3tan 45°+cos 60°
=2×-3×1+
=1-3+
=-.
(2)cos 245°-tan 30°·sin 60°
=()2-×
=-
=0.
15.解:如图,连接BC.∵AB是☉O的直径,∴∠ACB=90°.
∵∠B=∠D=26°,∴∠CAB=90°-26°=64°.
16.解:(1)把点M(-2,3)的坐标代入y=-x2+mx+3,得-4-2m+3=3,
解得m=-2,∴y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为(-1,4).
(2)∵y=-(x+1)2+4,∴抛物线开口向下,有最大值4.
∵当x=0时,y=3,当x=-3时,y=0,
∴当-3≤x≤0时,y的取值范围是0≤y≤4.
17.解:(1)p=500-10×(60-50)=400(盒),故答案为400;
解:(2)y=x[500-10(x-50)]=-10(x-50)2+25 000,
∴当x=50时,y有最大值25 000元.
答:当每盒售价定为50元时,日销售额y(元)最大,最大日销售额是25 000元.
18.(1)证明:如图,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.
又OB=OE,∴∠OEB=∠OBE,∴∠CBE=∠OEB,
∴BC∥OE,∴∠OEA=∠C=90°.
又点E在☉O上,∴AC是☉O的切线.
(2)解:设☉O的半径为r.
∵∠OEA=90°,∴AO2=AE2+OE2,即(r+2)2=42+r2,
解得r=3,∴☉O的半径为3.
19.解:(1)【观察探究】
由图象可知,当函数值为-1时,直线y=-1与图象交点的横坐标就是方程-(|x|-1)2=-1的解.
故答案为x=-2或x=0或x=2.
(2)【问题解决】
①若方程(-x|-1)2=a有四个实数根,由图象可知a的取值范围是-1<a<0.
故答案为-1<a<0.
②由图象可知:四个根中有两个互为相反数,另外两个也互为相反数,所以x1+x2+x3+x4=0.
故答案为0.
(3)【拓展延伸】
①平移后的图象如图所示.将函数y=-(|x|-1)2的图象先向右平移2个单位长度,再向上平移3个单位长度可得到函数y1=-(|x-2|-1)2+3的图象.
②当2≤y1≤3时,自变量x的取值范围是0≤x≤4.
故答案为0≤x≤4.
20.解:(1)∵AB=3 m,AD=BC=4 m,E(0,4),
∴A(-2,3),B(-2,0),C(2,0),D(2,3).
设抛物线的表达式为y=ax2+bx+c,
将A,D,E三点的坐标分别代入表达式,得
解得
∴抛物线的表达式为y=-x2+4.
(2)设G(-t,3),则L(-t-,3+),
∴3+=-(-t-)2+4,
解得t=(负值舍去),∴GM=2t=.
故两个正方形装置的间距GM的长为 m.
(3)取最右侧光线与抛物线切点为F,如图,
设直线AC的表达式为y=kx+b,
则解得
∴直线AC的表达式为y=-x+.
∵FK∥AC,设lFK:y=-x+m,联立
得-x2+x+4-m=0,
∴Δ=()2-4×(-)(4-m)=0,解得m=,
∴直线FK的表达式为y=-x+.
令y=0,得x=,即OK=,
∴CK=OK-OC=-2=.
故CK的长为 m.
第一部分 选择题
一、选择题(本大题共8小题,每小题3分,共24分)
1.计算sin 45°的值等于( )
A. B. C. D.
2.如图,AB是☉O的直径,C是☉O上一点.若∠BOC=66°,则∠A=( )
第2题图
A.66° B.33° C.24° D.30°
3.如图,某水库堤坝横断面迎水坡AB的坡角为α,堤坝高BC为50 m,则迎水坡面AB的长度是( )
第3题图
A.50·tan α m B.50·sin α m C. m D. m
4.如图,CD为☉O的直径,弦AB⊥CD于点E,CE=1,AB=6,则CD长为( )
第4题图
A.10 B.9 C.8 D.5
5.如图,二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B两点,对称轴是直线x=1,下列说法正确的是( )
第5题图
A.a>1 B.当x>-1时,y的值随x值的增大而增大
C.点B的坐标为(4,0) D.4a+2b+c>0
6.如图,☉C过原点O,且与两坐标轴分别交于A,B两点,点A的坐标为(0,5),点M是第三象限内上一点,∠BMO=120°,则☉O的半径为( )
第6题图
A.4 B.5 C.6 D.2
7.如图,客轮在海上以30 km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1 h后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是( )
第7题图
A. 15 km B. 15 km C. 15(+)km D.5(3+)km
8.苏州园林中的月亮门是中国古典园林住宅中常见的圆弧形洞门(如图1),因圆形如月而得名.月亮门因其寓意美好且造型独特,被广泛使用.图2是小明同学家中的月亮门示意图,经测量,水平跨径AB为2.4米,水平木条BD和铅锤木条CD长都为0.4米,点C恰好落在☉O上,则此月亮门的半径为( )
第8题图
A.2.1米 B.2.0米 C.1.9米 D.1.8米
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
9.如图,在△ABC中,∠ACB=90°,BC=12,AB=15,则cos B的值为 .
第9题图
10.请写出一个开口向上,经过点(0,4)的抛物线的表达式 .
11.如图,AD切☉O于A点,BC为直径,连接CA,已知∠ACB=20°,则∠CAD的度数为 .
第11题图
12.如图,在菱形ABCD中,分别以点A,C为圆心,AD,CB的长为半径画弧,分别交对角线AC于点E,F.若AB=4,∠ABC=120°,则图中阴影部分的面积为 .(结果保留π)
第12题图
13.如图,抛物线y=-x2+2x+3交x轴于A,B两点,交y轴于点C,点D为抛物线的顶点,点C关于抛物线的对称轴的对称点为E,点G,F分别在x轴和y轴上,则四边形EDFG周长的最小值为 .
第13题图
三、解答题(本大题共7小题,共61分)
14.(6分)计算.
(1)2sin 30°-3tan 45°+cos 60°;
(2)co45°-tan 30°·sin 60°.
15.(6分)如图,AB是☉O的直径,弦CD与AB相交于点E,∠ADC=26°,求∠CAB的度数.
16.(8分)如图,已知抛物线y=-x2+mx+3经过点M(-2,3).
(1)求m的值,并求出此抛物线的顶点坐标;
(2)当-3≤x≤0时,直接写出y的取值范围.
17.(8分)“端午节”吃粽子是中国的传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒的利润率不低于50%,且每盒售价不得高于80元.根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒.设每盒售价为x元,日销售量为p盒.
(1)当x=60时,p= ;
(2)当每盒售价定为多少元时,日销售额y(元)最大?最大日销售额是多少元?
18.(9分)如图,在△ABC中,∠C=90°,点E在AC边上,BE平分∠ABC,DE⊥BE交AB于点D,☉O是△BDE的外接圆.
(1)求证:AC是☉O的切线;
(2)若AD=2,AE=4,求☉O的半径长.
19.(12分)数形结合是解决数学问题的重要方法.小明同学学习二次函数后,对函数y=-(|x|-1)2进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:
【观察探究】
方程-(|x|-1)2=-1的解为 ;
【问题解决】
若方程-(|x|-1)2=a有四个实数根,分别为x1,x2,x3,x4.
①a的取值范围是 ;
②计算x1+x2+x3+x4= ;
【拓展延伸】
①将函数y=-(|x|-1)2的图象经过怎样的平移可得到函数y1=-(|x-2|-1)2+3的图象?画出平移后的图象并写出平移过程;
②观察平移后的图象,当2≤y1≤3时,直接写出自变量x的取值范围 .
20.(12分)蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它的出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图1,某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成,其中AB=3 m,BC=4 m,取BC的中点O,过点O作线段BC的垂直平分线OE交抛物线AED于点E,若以O点为原点,BC所在直线为x轴,OE为y轴建立如图所示平面直角坐标系.
请回答下列问题:
(1)如图2,抛物线AED的顶点E(0,4),求抛物线的表达式;
(2)如图3,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置LFGT,SMNR,若FL=NR=0.75 m,求两个正方形装置的间距GM的长;
(3)如图4,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为CK,求CK的长.
参考答案
1.C 2.B 3.D 4.A 5.D 6.B 7.D 8.B
9. 10.y=x2+4(答案不唯一) 11.70° 12.8-
13.+ 解析:如图,在y=-x2+2x+3中,当x=0时,y=3,即点C(0,3).
∵y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1,顶点D(1,4),
则点C关于对称轴的对称点E的坐标为(2,3).
作点D关于y轴的对称点D'(-1,4),作点E关于x轴的对称点E'(2,-3).
连接D'E',与x轴交于点G,与y轴交于点F,则点G,F即为使四边形EDFG的周长最小的点,四边形EDFG的周长=DE+DF+FG+GE=DE+D'F+FG+GE'=DE+D'E'
=+=+,
∴四边形EDFG的周长的最小值为+.
14.解:(1)2sin 30°-3tan 45°+cos 60°
=2×-3×1+
=1-3+
=-.
(2)cos 245°-tan 30°·sin 60°
=()2-×
=-
=0.
15.解:如图,连接BC.∵AB是☉O的直径,∴∠ACB=90°.
∵∠B=∠D=26°,∴∠CAB=90°-26°=64°.
16.解:(1)把点M(-2,3)的坐标代入y=-x2+mx+3,得-4-2m+3=3,
解得m=-2,∴y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为(-1,4).
(2)∵y=-(x+1)2+4,∴抛物线开口向下,有最大值4.
∵当x=0时,y=3,当x=-3时,y=0,
∴当-3≤x≤0时,y的取值范围是0≤y≤4.
17.解:(1)p=500-10×(60-50)=400(盒),故答案为400;
解:(2)y=x[500-10(x-50)]=-10(x-50)2+25 000,
∴当x=50时,y有最大值25 000元.
答:当每盒售价定为50元时,日销售额y(元)最大,最大日销售额是25 000元.
18.(1)证明:如图,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.
又OB=OE,∴∠OEB=∠OBE,∴∠CBE=∠OEB,
∴BC∥OE,∴∠OEA=∠C=90°.
又点E在☉O上,∴AC是☉O的切线.
(2)解:设☉O的半径为r.
∵∠OEA=90°,∴AO2=AE2+OE2,即(r+2)2=42+r2,
解得r=3,∴☉O的半径为3.
19.解:(1)【观察探究】
由图象可知,当函数值为-1时,直线y=-1与图象交点的横坐标就是方程-(|x|-1)2=-1的解.
故答案为x=-2或x=0或x=2.
(2)【问题解决】
①若方程(-x|-1)2=a有四个实数根,由图象可知a的取值范围是-1<a<0.
故答案为-1<a<0.
②由图象可知:四个根中有两个互为相反数,另外两个也互为相反数,所以x1+x2+x3+x4=0.
故答案为0.
(3)【拓展延伸】
①平移后的图象如图所示.将函数y=-(|x|-1)2的图象先向右平移2个单位长度,再向上平移3个单位长度可得到函数y1=-(|x-2|-1)2+3的图象.
②当2≤y1≤3时,自变量x的取值范围是0≤x≤4.
故答案为0≤x≤4.
20.解:(1)∵AB=3 m,AD=BC=4 m,E(0,4),
∴A(-2,3),B(-2,0),C(2,0),D(2,3).
设抛物线的表达式为y=ax2+bx+c,
将A,D,E三点的坐标分别代入表达式,得
解得
∴抛物线的表达式为y=-x2+4.
(2)设G(-t,3),则L(-t-,3+),
∴3+=-(-t-)2+4,
解得t=(负值舍去),∴GM=2t=.
故两个正方形装置的间距GM的长为 m.
(3)取最右侧光线与抛物线切点为F,如图,
设直线AC的表达式为y=kx+b,
则解得
∴直线AC的表达式为y=-x+.
∵FK∥AC,设lFK:y=-x+m,联立
得-x2+x+4-m=0,
∴Δ=()2-4×(-)(4-m)=0,解得m=,
∴直线FK的表达式为y=-x+.
令y=0,得x=,即OK=,
∴CK=OK-OC=-2=.
故CK的长为 m.
