第三章 圆 重难点分类练(含答案)2025-2026学年数学北师大版九年级下册
文档属性
| 名称 | 第三章 圆 重难点分类练(含答案)2025-2026学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:58:30 | ||
图片预览




文档简介
第三章 圆
. . . . . . . . . . . . . . . . . . . .
对有关概念的理解错误
【例1】下列命题中,是真命题的是( ).
A.三角形的外心是三角形三个内角平分线的交点
B.过一点有且只有一条直线与已知直线平行
C.连接对角线相等的四边形各边中点所得四边形是矩形
D.一组对边平行,一组对角相等的四边形是平行四边形
三角形的内心与外心是常考知识点,①三角形的内心是三角形三条角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“I”表示.②三角形的外心是三角形三边垂直平分线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用O表示.③任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;④解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即S=Pr(S为三角形的面积,P为三角形的周长,r为内切圆的半径).
1.下列说法正确的是( ).
A.三点确定一个圆 B.三角形的内心到三角形三个顶点的距离相等
C.相等的圆心角所对的弧相等 D.直角三角形的外心为斜边的中点
垂径定理理解错误
【例2】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”.阅读完这段文字后,小智画出了一个圆柱截面示意图,其中BO⊥CD于点A,问径就是要求☉O的直径.再次阅读后,发现AB=2寸,CD=10寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请帮助小智求出☉O的直径.
在垂经定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)
2.如图,☉O的直径AB与弦CD交于点E,∠DEB=30°,AE=2,EB=6,求CD的长.
圆心角与圆周角定理的理解与应用的错误
【例3】 (2023·深圳市宝安区11校联考)如图,四边形ABCD是☉O的内接四边形,连接AO,CO,DO,若∠AOC=112°,则∠B的度数是( ).
A.56° B.114° C.124° D.134°
同一条弧所对的圆周角是圆心角度数的一半,注意理解它们的倍分关系,圆周角定理成立的前提条件是在同圆或等圆中.
3.(2024·龙华区二模)如图,点A,B,C在☉O上,AC平分∠OAB,若∠OAB=40°,则∠CBD= °.
正多边形的有关计算及弧长、扇形面积公式的运用错误
【例4】(2023·深圳龙岗九年级统考期末)已知四个正六边形如图摆放在图中,顶点A,B,C,D,E,F在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( ).
A.3- B. C. D.
本节比较容易出现概念性的错误,①正多边形的半径是指正多边形的外接圆的半径,正多边形的边心距是正多边形内切圆的半径;②对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即×πR2=;③在扇形面积公式中涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量;④扇形面积公式S扇形=lR,可根据题目条件灵活选择使用,它与三角形面积公式S=ah有点类似,可类比记忆;④扇形两个面积公式之间的联系:S扇形==××R=lR.
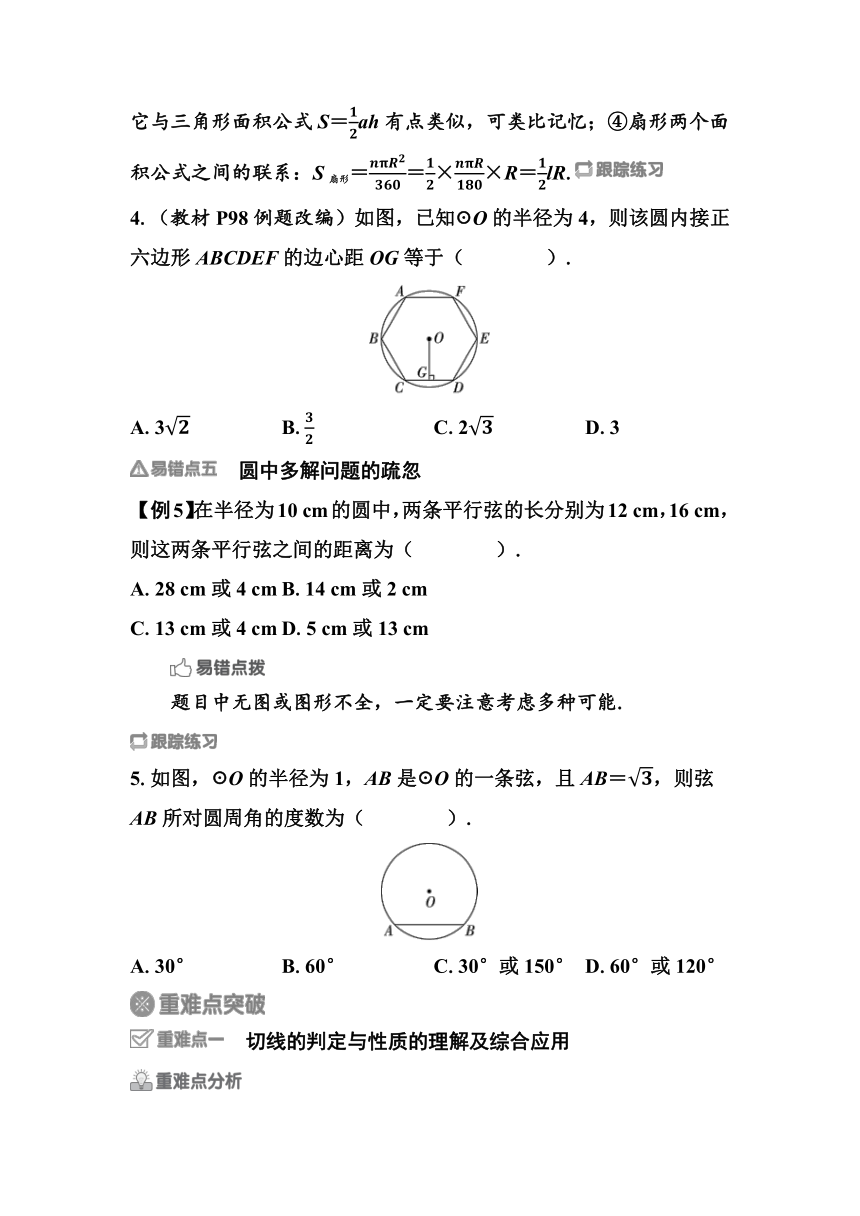
4.(教材P98例题改编)如图,已知☉O的半径为4,则该圆内接正六边形ABCDEF的边心距OG等于( ).
A.3 B. C.2 D.3
圆中多解问题的疏忽
【例5】在半径为10 cm的圆中,两条平行弦的长分别为12 cm,16 cm,则这两条平行弦之间的距离为( ).
A.28 cm或4 cm B.14 cm或2 cm
C.13 cm或4 cm D.5 cm或13 cm
题目中无图或图形不全,一定要注意考虑多种可能.
5.如图,☉O的半径为1,AB是☉O的一条弦,且AB=,则弦AB所对圆周角的度数为( ).
A.30° B.60° C.30°或150° D.60°或120°
切线的判定与性质的理解及综合应用
切线的判定与性质是中考必考考点之一,注意区分.
(1)切线的判定:
①经过半径的外端并且垂直于这条半径的直线是圆的切线.
②到圆心的距离d等于圆的半径的直线是圆的切线.
(2)切线的性质:
①圆的切线垂直于过切点的半径.
②经过圆心作圆的切线的垂线经过切点.
③经过切点作切线的垂线经过圆心.
(3)本节是考试的重点和难点之一,综合性强,注意各知识点间的联系.
1.(2024·南山区一模)如图,☉O是△ABC的外接圆,AD是☉O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.
(1)求证:CF是☉O的切线;
(2)若直径AD=10,cos B=,求FD的长.
2.如图,在Rt△ABC中,∠ABC=90°,点O,D分别在AB,AC上,CD=CB,☉O经过点B,D,弦DF⊥AB于点E,连接BF.
(1)求证:AC为☉O的切线;
(2)若∠C=60°,BF=3,求DF的长.
3.(2024·深圳模拟)如图,AB是☉O的直径,弦CD与AB交于点E,连接DB,AC,过点C作DB的垂线,交DB的延长线于点F,且∠ABD=2∠BDC.
(1)求证:CF是☉O的切线;
(2)若☉O的半径为,tan∠BDC=,求线段OE的长.
三角形的内心与外心
(1)三角形外接圆的圆心叫三角形的外心,锐角三角形的外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形的外心在三角形外部.
(2)三角形的内心是三角形内切圆的圆心,是三角形三个内角平分线的交点,它到三角形三边的距离相等.
4.如图,△ABC的内切圆☉O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( ).
A. B. C. D.
5.以下列三边长度作出的三角形中,其内切圆半径最小的是( ).
A.8,8,8 B.4,10,10 C.5,9,10 D.6,8,10
6.(1)如图1,在△ABC中,∠A=120°,AB=AC=5.尺规作图:作△ABC的外接圆☉O,并直接写出△ABC的外接圆半径R的长.
(2)如图2,☉O的半径为13,弦AB=24,M是AB的中点,P是☉O上一动点,求PM的最大值.
(3)如图3所示,AB,AC,是某新区的三条规划路,其中AB=6 km,AC=3 km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E,F,也就是分别在、线段AB和AC上选取点P,E,F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE,EF和FP.为了快捷、环保和节约成本.要使得线段PE,EF,FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
路径与最值的探寻
圆中的最值与路径问题的关键就是要根据题中所给的条件确定动点的轨迹,通常是用圆的定义,即到定点的距离等于定长来确定动点所在圆的圆心和半径.
7.(2023·深圳宝安区第一外国语学校一模)如图,在△ABC 中,AB=AC=10,BC=16,点 O 是△ABC 的重心,将线段 AO 绕点 A 逆时针旋转至点O', D 为线段 CO'的中点,连接 BD,则 BD 的最大值为 .
8.如图,☉O的直径AB=10,弦BC=2,点P是☉O上的一动点(不与点A,B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
(1)求tan∠BPC的值.
(2)随着点P的运动,的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值.
(3)运动过程中,AP+2BP的最大值是多少?请你直接写出来.
9.【综合与实践】
数学活动课上,老师出示了一个问题:如图,已知三只蚂蚁A,B,C在半径为1的☉O上静止不动,第四只蚂蚁P在☉O上移动,并始终保持∠APC=∠CPB=60°.
(1)请判断△ABC的形状,“数学希望小组”很快得出结论,请你回答这个结论:△ABC是 三角形;
(2)“数学智慧小组”继续研究发现:当第四只蚂蚁P在☉O上移动时,线段PA,PB,PC三者之间存在一种数量关系.请你写出这种数量关系,并加以证明;
(3)“数学攀峰小组”突发奇想,深入探究发现:若第五只蚂蚁M同时随着蚂蚁P的移动而移动,且始终位于线段PC的中点,在这个运动过程中,线段BM的长度一定存在最小值,请你求出线段BM的最小值.(不写解答过程,直接写出结果)
参考答案
【思维导图】
①轴对称 ②中心对称 ③相等 ④平分 ⑤一半 ⑥相等 ⑦直角 ⑧90° ⑨互补 ⑩三 垂直平分线 圆上 相切 垂直 外端 垂直 相等 角平分线 三边 l= S扇形==lr
【例1】D 解析:A.三角形的外心是三角形三边垂直平分线的交点,三角形三个内角平分线的交点是三角形的内心,故为假命题,不符合题意;B.在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故为假命题,不符合题意;C.对角线相等的四边形各边中点连线所得四边形不一定是矩形,故为假命题,不符合题意;D.一组对边平行,一组对角相等的四边形是平行四边形,为真命题,符合题意.故选D.
1.D
【例2】解:如图,连接OC,∵OB⊥CD,垂足为A,
∴CA=CD=5寸,设CO=x寸,则AO=(x-2)寸.在Rt△AOC中,∠CAO=90°,
∴OA2+CA2=OC2,
∴(x-2)2+52=x2,解得x=,
∴×2=(寸),
∴☉O的直径为寸.
2.解:如图,过点O作OF⊥CD交CD于点F,连接OD,则F为CD的中点,
∴CF=DF,CD=2DF.∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2.在Rt△OEF中,∠DEB=30°,
∴OF=OE=1.在Rt△ODF中,OF=1,OD=4,根据勾股定理得DF===,
∴CD=2DF=2.
【例3】C
3.70 解析:如图,延长AO交☉O于点E,连接BE,
则∠ABE=90°,
∵∠OAB=40°,
∴∠E=90°-∠OAB=50°,
∴∠C=∠E=50°.
∵AC平分∠OAB,
∴∠CAB=∠OAB=20°,
∴∠CBD=∠CAB+∠C=20°+50°=70°,
故答案为70.
【例4】D 解析:如图,连接AD交PM于点O,则点O是圆心,过点O作ON⊥DE于点N,连接MF,取MF的中点G,连接GH,GQ,由对称性可知,OM=OP=EN=DN=1,由正六边形的性质可得ON=2,
∴OD===OF,
∴MF=-1.由正六边形的性质可知,△GFH,△GHQ,△GQM都是正三角形,
∴FH=MF=,故选D.
4.C
【例5】B 解析:有两种情况:①如图1,当AB和CD在点O的两旁时,过点O作MN⊥AB于点M,交CD于点N,连接OB,OD,∵AB∥CD,
∴MN⊥CD.由垂径定理得,BM=AB=8 cm,DN=CD=6 cm.∵OB=OD=10 cm,由勾股定理得OM==6 cm,同理ON=8 cm,
∴MN=8+6=14(cm);②当AB和CD在圆心O的同旁时,如图2,MN=8-6=2(cm),故选B.
图1 图2
5.D
【重难点突破】
1.(1)证明:如图,连接OC,
∵AD是☉O的直径,
∴∠ACD=90°,
∴∠ADC+∠CAD=90°.
∵OC=OD,
∴∠ADC=∠OCD.
又∵∠DCF=∠CAD,
∴∠DCF+∠OCD=90°,即OC⊥FC.
∴FC是☉O的切线.
(2)解:∵∠B=∠ADC,cos B=,
∴cos∠ADC=.
在Rt△ACD中,∵cos∠ADC==,AD=10,
∴CD=AD·cos∠ADC=10×=6,
∴AC==8,
∴=.
∵∠FCD=∠FAC,∠F=∠F,
∴△FCD∽△FAC,
∴===,
设FD=3x,则FC=4x,AF=3x+10,
又∵FC2=FD·FA,即(4x)2=3x(3x+10),
解得x=(取正值),
∴FD=3x=.
2.(1)证明:如图,连接OD,OC,∵CD=CB,OD=OB,OC=OC,
∴△OBC≌△ODC(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥AC,
∴AC是☉O的切线.
(2)解:在四边形OBCD中,∠ODC=∠OBC=90°.∵∠BCD=60°,
∴∠BOD=120°,
∴∠F=∠BOD=60°.∵DF⊥AB,
∴EF=BFcos 60°=3×=,
∴DF=2EF=3.
3.(1)证明:如图,连接OC,则∠BOC=2∠BDC,
∵∠ABD=2∠BDC,
∴∠BOC=∠ABD,
∴OC∥DB.
∵CF⊥DB,
∴∠F=90°,
∴∠OCF=180°-∠F=90°.
∵OC是☉O的半径,且CF⊥OC,
∴CF是☉O的切线.
(2)解:∵AB是☉O的直径,☉O的半径为,
∴∠ACB=90°,OC=OB=,AB=2.
∵∠A=∠BDC,
∴=tan A=tan∠BDC=,
∴AC=2BC,
∴AB===BC=2,
∴BC=2.
∵∠FCB+∠OCB=90°,∠A+∠ABC=90°,
且∠OCB=∠ABC,
∴∠FCB=∠A=∠BDC,
∴=tan∠FCB=tan∠BDC==,
∴CF=2BF,
∴BC===BF=2,
∴BF=,
∴DF=2CF=4BF=4×=,
∴BD=DF-BF=-=.
∵OC∥DB,
∴△OCE∽△BDE,
∴===,
∴OE=OB=×=,
∴线段OE的长是.
4.D
5.B 解析:选项A,如图1,设三角形的内心为O,分别过点O作三边的垂线,垂足为D,E,F,连接OA,OB,OC,
∴OD=OE=OF=r,
∴S△ABC=S△AOB+S△BOC+S△AOC=OF·AB+OD·BC+OE·AC=r(AB+BC+AC).∴三角形内切圆半径r=.∵三角形是等边三角形,
∴S=×82=16,
∴三角形内切圆半径rA===;选项B,如图2,△ABC中,AB=AC=10,BC=4,过A作AD⊥BC于D,
∴CD=BC=2,
∴AD===4,
∴S△ABC=AD·BC=×4×4=8,
∴三角形内切圆半径rB===;选项C,如图3,△ABC中,AB=10,AC=9,BC=5,过点A作AD⊥BC于点D,设CD=x,则BD=5-x,∵AD2=AB2-BD2=AC2-CD2,
∴AD2=102-(5-x)2=92-x2,解得x=,AD==,
∴S△ABC=AD·BC=×5×=6,
∴三角形内切圆半径rC===;选项D,△ABC中,AB=10,AC=8,BC=6,
∴AB2=100=AC2+BC2,
∴△ABC是直角三角形,
∴S△ABC=AC·BC=×8×6=24,
∴三角形内切圆半径rD===2.∵<<2<,
∴内切圆半径最小的是4,10,10.故选B.
图1 图2 图3
6.解:(1)如图1,外接圆的圆心为O,连接OA,OB,∵O是等腰三角形的外心,AB=AC,
∴∠BAO=∠OAC=∠BAC=×120°=60°.∵OA=OB,
∴△AOB是等边三角形,
∴OB=AB=5,故△ABC外接圆半径R的长为5.
(2)如图2所示,连接MO并延长交☉O于点N,连接OP,显然MP≤OM+OP=OM+ON=MN.∵AB=24,M是AB的中点,
∴MN⊥AB,AM=MB=12.∵ON=13,
∴OM===5.∴MN=18,
∴PM的最大值为18.
(3)如图3所示,假设P点即为所求点,分别作出点P关于AB,AC的对称点P',P″,连接PP',P'E,PE,PF,PP″,由对称性可知PE+EF+FP=P'E+EF+FP″=P'P″,且P',E,F,P″在一条直线上,所以P'P″即为最短距离,其长度取决于PA的长度, 如图④,作出的圆心O,连接AO,与弧BC交于点P,P点即为使得PA最短的点,∵AB=6 km,AC=3 km,∠BAC=60°,
∴△ABC是直角三角形,∠ABC=30°,BC=3,所对的圆心角为60°,
∴△OBC是等边三角形,∠CBO=60°,BO=BC=3,
∴∠ABO=90°,AO==3,PA=3-3,∠P'AE=∠EAP,∠PAF=∠FAP″,
∴∠P'AP″=2∠ABC=120°,P'A=AP″,
∴∠AP'E=∠AP″F=30°,∵P'P″=2P'Acos ∠AP'E=P'A=3-9,
∴PE+EF+FP的最小值为(3-9)km.
7.3+2 解析:如图,延长AO交BC于点E,延长CB到点F,使BF=BC.∵BF=BC,
∴B是CF的中点.∵D 为线段 CO'的中点,
∴BD是△CF O'的中位线,
∴BD=F O'.∵线段 AO绕点A逆时针旋转至O',
∴点O'在以点A为圆心,AO为半径的圆上运动.如图,当点F,O',A在同一条直线上时,FO'最长,BD=F O'最大.∵点O是△ABC的重心,
∴AE是△ABC的中线,
∴BE=CE=BC=8.∵AB=AC,
∴△ABC是等腰三角形,
∴AE⊥BC,
∴∠AEB=90°.∵AB=10,
∴AE===6.∵O为△ABC的重心,
∴AO=AE=4.∵BF=BC=16,BE=8,
∴EF=BE+BF=24,
∴AF===6.由旋转的性质知AO'=AO=4,
∴FO'=FA+AO'=6+4,
∴BD=FO'=(6+4)=3+2,即BD 的最大值为3+2,故答案为3+2.
8.解:(1)如图,连接AC,∵AB是☉O的直径,
∴∠ACB=90°.在Rt△ABC中,AB=10,BC=2,
∴AC==4,
∴tan ∠BPC=tan ∠BAC==.
(2)的值不会发生变化,理由如下:∵∠PCD=∠ACB=90°,
∴∠1+∠PCB=∠2+∠PCB,
∴∠1=∠2.∵∠3是圆内接四边形APBC的一个外角,
∴∠3=∠PAC,
∴△CBD∽△CAP,
∴=.在Rt△PCD中,=tan∠BPC=,
∴==.
(3)由(2)知BD=AP,
∴AP+2BP=2=2(BD+BP)=2PD=.由tan∠BPC=,得cos∠BPC=,
∴AP+2BP=PC≤AB=10,
∴AP+2BP的最大值为10.
9.解:(1)∵∠APC=∠CPB=60°,
∴,对应的圆周角为60°,
∴∠ABC=60°,∠BAC=60°,
∴∠ACB=180°-60°-60°=60°,
∴△ABC为等边三角形.故答案为等边.
(2)PC=PA+PB.理由:如图1,在PC上截取PD=AP,连接AD,∵∠APC=60°,
∴△APD为等边三角形,
∴AD=AP=PD,∠ADP=60°,∠ADC=120°.∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB.在△APB和△ADC中,∴△APB≌△ADC(AAS),
∴BP=CD.∵PD=AP,
∴PC=PA+PB.
解:(3)如图2,根据题意可知,M的轨迹是以OC为直径的圆,设圆心为O',连接BO',过点O'作O'N⊥BC于点N,过点O作OQ⊥BC于点Q,
∴∠O'CB=30°,O'C=,
∴O'N=,CN=,
∴O'N∥OQ.∵O'是OC的中点,
∴O'N是三角形OQC的中位线,
∴N为CQ的中点,
∴CQ=2CN=.又∵Q是BC的中点,
∴BC=2CQ=,
∴BN=BC-CN=-=,
∴BO'===,
∴BM最小=BO'-O'M=-.
图1 图2
. . . . . . . . . . . . . . . . . . . .
对有关概念的理解错误
【例1】下列命题中,是真命题的是( ).
A.三角形的外心是三角形三个内角平分线的交点
B.过一点有且只有一条直线与已知直线平行
C.连接对角线相等的四边形各边中点所得四边形是矩形
D.一组对边平行,一组对角相等的四边形是平行四边形
三角形的内心与外心是常考知识点,①三角形的内心是三角形三条角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“I”表示.②三角形的外心是三角形三边垂直平分线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用O表示.③任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;④解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即S=Pr(S为三角形的面积,P为三角形的周长,r为内切圆的半径).
1.下列说法正确的是( ).
A.三点确定一个圆 B.三角形的内心到三角形三个顶点的距离相等
C.相等的圆心角所对的弧相等 D.直角三角形的外心为斜边的中点
垂径定理理解错误
【例2】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”.阅读完这段文字后,小智画出了一个圆柱截面示意图,其中BO⊥CD于点A,问径就是要求☉O的直径.再次阅读后,发现AB=2寸,CD=10寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请帮助小智求出☉O的直径.
在垂经定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)
2.如图,☉O的直径AB与弦CD交于点E,∠DEB=30°,AE=2,EB=6,求CD的长.
圆心角与圆周角定理的理解与应用的错误
【例3】 (2023·深圳市宝安区11校联考)如图,四边形ABCD是☉O的内接四边形,连接AO,CO,DO,若∠AOC=112°,则∠B的度数是( ).
A.56° B.114° C.124° D.134°
同一条弧所对的圆周角是圆心角度数的一半,注意理解它们的倍分关系,圆周角定理成立的前提条件是在同圆或等圆中.
3.(2024·龙华区二模)如图,点A,B,C在☉O上,AC平分∠OAB,若∠OAB=40°,则∠CBD= °.
正多边形的有关计算及弧长、扇形面积公式的运用错误
【例4】(2023·深圳龙岗九年级统考期末)已知四个正六边形如图摆放在图中,顶点A,B,C,D,E,F在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( ).
A.3- B. C. D.
本节比较容易出现概念性的错误,①正多边形的半径是指正多边形的外接圆的半径,正多边形的边心距是正多边形内切圆的半径;②对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即×πR2=;③在扇形面积公式中涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量;④扇形面积公式S扇形=lR,可根据题目条件灵活选择使用,它与三角形面积公式S=ah有点类似,可类比记忆;④扇形两个面积公式之间的联系:S扇形==××R=lR.
4.(教材P98例题改编)如图,已知☉O的半径为4,则该圆内接正六边形ABCDEF的边心距OG等于( ).
A.3 B. C.2 D.3
圆中多解问题的疏忽
【例5】在半径为10 cm的圆中,两条平行弦的长分别为12 cm,16 cm,则这两条平行弦之间的距离为( ).
A.28 cm或4 cm B.14 cm或2 cm
C.13 cm或4 cm D.5 cm或13 cm
题目中无图或图形不全,一定要注意考虑多种可能.
5.如图,☉O的半径为1,AB是☉O的一条弦,且AB=,则弦AB所对圆周角的度数为( ).
A.30° B.60° C.30°或150° D.60°或120°
切线的判定与性质的理解及综合应用
切线的判定与性质是中考必考考点之一,注意区分.
(1)切线的判定:
①经过半径的外端并且垂直于这条半径的直线是圆的切线.
②到圆心的距离d等于圆的半径的直线是圆的切线.
(2)切线的性质:
①圆的切线垂直于过切点的半径.
②经过圆心作圆的切线的垂线经过切点.
③经过切点作切线的垂线经过圆心.
(3)本节是考试的重点和难点之一,综合性强,注意各知识点间的联系.
1.(2024·南山区一模)如图,☉O是△ABC的外接圆,AD是☉O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.
(1)求证:CF是☉O的切线;
(2)若直径AD=10,cos B=,求FD的长.
2.如图,在Rt△ABC中,∠ABC=90°,点O,D分别在AB,AC上,CD=CB,☉O经过点B,D,弦DF⊥AB于点E,连接BF.
(1)求证:AC为☉O的切线;
(2)若∠C=60°,BF=3,求DF的长.
3.(2024·深圳模拟)如图,AB是☉O的直径,弦CD与AB交于点E,连接DB,AC,过点C作DB的垂线,交DB的延长线于点F,且∠ABD=2∠BDC.
(1)求证:CF是☉O的切线;
(2)若☉O的半径为,tan∠BDC=,求线段OE的长.
三角形的内心与外心
(1)三角形外接圆的圆心叫三角形的外心,锐角三角形的外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形的外心在三角形外部.
(2)三角形的内心是三角形内切圆的圆心,是三角形三个内角平分线的交点,它到三角形三边的距离相等.
4.如图,△ABC的内切圆☉O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( ).
A. B. C. D.
5.以下列三边长度作出的三角形中,其内切圆半径最小的是( ).
A.8,8,8 B.4,10,10 C.5,9,10 D.6,8,10
6.(1)如图1,在△ABC中,∠A=120°,AB=AC=5.尺规作图:作△ABC的外接圆☉O,并直接写出△ABC的外接圆半径R的长.
(2)如图2,☉O的半径为13,弦AB=24,M是AB的中点,P是☉O上一动点,求PM的最大值.
(3)如图3所示,AB,AC,是某新区的三条规划路,其中AB=6 km,AC=3 km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E,F,也就是分别在、线段AB和AC上选取点P,E,F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE,EF和FP.为了快捷、环保和节约成本.要使得线段PE,EF,FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
路径与最值的探寻
圆中的最值与路径问题的关键就是要根据题中所给的条件确定动点的轨迹,通常是用圆的定义,即到定点的距离等于定长来确定动点所在圆的圆心和半径.
7.(2023·深圳宝安区第一外国语学校一模)如图,在△ABC 中,AB=AC=10,BC=16,点 O 是△ABC 的重心,将线段 AO 绕点 A 逆时针旋转至点O', D 为线段 CO'的中点,连接 BD,则 BD 的最大值为 .
8.如图,☉O的直径AB=10,弦BC=2,点P是☉O上的一动点(不与点A,B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
(1)求tan∠BPC的值.
(2)随着点P的运动,的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值.
(3)运动过程中,AP+2BP的最大值是多少?请你直接写出来.
9.【综合与实践】
数学活动课上,老师出示了一个问题:如图,已知三只蚂蚁A,B,C在半径为1的☉O上静止不动,第四只蚂蚁P在☉O上移动,并始终保持∠APC=∠CPB=60°.
(1)请判断△ABC的形状,“数学希望小组”很快得出结论,请你回答这个结论:△ABC是 三角形;
(2)“数学智慧小组”继续研究发现:当第四只蚂蚁P在☉O上移动时,线段PA,PB,PC三者之间存在一种数量关系.请你写出这种数量关系,并加以证明;
(3)“数学攀峰小组”突发奇想,深入探究发现:若第五只蚂蚁M同时随着蚂蚁P的移动而移动,且始终位于线段PC的中点,在这个运动过程中,线段BM的长度一定存在最小值,请你求出线段BM的最小值.(不写解答过程,直接写出结果)
参考答案
【思维导图】
①轴对称 ②中心对称 ③相等 ④平分 ⑤一半 ⑥相等 ⑦直角 ⑧90° ⑨互补 ⑩三 垂直平分线 圆上 相切 垂直 外端 垂直 相等 角平分线 三边 l= S扇形==lr
【例1】D 解析:A.三角形的外心是三角形三边垂直平分线的交点,三角形三个内角平分线的交点是三角形的内心,故为假命题,不符合题意;B.在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故为假命题,不符合题意;C.对角线相等的四边形各边中点连线所得四边形不一定是矩形,故为假命题,不符合题意;D.一组对边平行,一组对角相等的四边形是平行四边形,为真命题,符合题意.故选D.
1.D
【例2】解:如图,连接OC,∵OB⊥CD,垂足为A,
∴CA=CD=5寸,设CO=x寸,则AO=(x-2)寸.在Rt△AOC中,∠CAO=90°,
∴OA2+CA2=OC2,
∴(x-2)2+52=x2,解得x=,
∴×2=(寸),
∴☉O的直径为寸.
2.解:如图,过点O作OF⊥CD交CD于点F,连接OD,则F为CD的中点,
∴CF=DF,CD=2DF.∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2.在Rt△OEF中,∠DEB=30°,
∴OF=OE=1.在Rt△ODF中,OF=1,OD=4,根据勾股定理得DF===,
∴CD=2DF=2.
【例3】C
3.70 解析:如图,延长AO交☉O于点E,连接BE,
则∠ABE=90°,
∵∠OAB=40°,
∴∠E=90°-∠OAB=50°,
∴∠C=∠E=50°.
∵AC平分∠OAB,
∴∠CAB=∠OAB=20°,
∴∠CBD=∠CAB+∠C=20°+50°=70°,
故答案为70.
【例4】D 解析:如图,连接AD交PM于点O,则点O是圆心,过点O作ON⊥DE于点N,连接MF,取MF的中点G,连接GH,GQ,由对称性可知,OM=OP=EN=DN=1,由正六边形的性质可得ON=2,
∴OD===OF,
∴MF=-1.由正六边形的性质可知,△GFH,△GHQ,△GQM都是正三角形,
∴FH=MF=,故选D.
4.C
【例5】B 解析:有两种情况:①如图1,当AB和CD在点O的两旁时,过点O作MN⊥AB于点M,交CD于点N,连接OB,OD,∵AB∥CD,
∴MN⊥CD.由垂径定理得,BM=AB=8 cm,DN=CD=6 cm.∵OB=OD=10 cm,由勾股定理得OM==6 cm,同理ON=8 cm,
∴MN=8+6=14(cm);②当AB和CD在圆心O的同旁时,如图2,MN=8-6=2(cm),故选B.
图1 图2
5.D
【重难点突破】
1.(1)证明:如图,连接OC,
∵AD是☉O的直径,
∴∠ACD=90°,
∴∠ADC+∠CAD=90°.
∵OC=OD,
∴∠ADC=∠OCD.
又∵∠DCF=∠CAD,
∴∠DCF+∠OCD=90°,即OC⊥FC.
∴FC是☉O的切线.
(2)解:∵∠B=∠ADC,cos B=,
∴cos∠ADC=.
在Rt△ACD中,∵cos∠ADC==,AD=10,
∴CD=AD·cos∠ADC=10×=6,
∴AC==8,
∴=.
∵∠FCD=∠FAC,∠F=∠F,
∴△FCD∽△FAC,
∴===,
设FD=3x,则FC=4x,AF=3x+10,
又∵FC2=FD·FA,即(4x)2=3x(3x+10),
解得x=(取正值),
∴FD=3x=.
2.(1)证明:如图,连接OD,OC,∵CD=CB,OD=OB,OC=OC,
∴△OBC≌△ODC(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥AC,
∴AC是☉O的切线.
(2)解:在四边形OBCD中,∠ODC=∠OBC=90°.∵∠BCD=60°,
∴∠BOD=120°,
∴∠F=∠BOD=60°.∵DF⊥AB,
∴EF=BFcos 60°=3×=,
∴DF=2EF=3.
3.(1)证明:如图,连接OC,则∠BOC=2∠BDC,
∵∠ABD=2∠BDC,
∴∠BOC=∠ABD,
∴OC∥DB.
∵CF⊥DB,
∴∠F=90°,
∴∠OCF=180°-∠F=90°.
∵OC是☉O的半径,且CF⊥OC,
∴CF是☉O的切线.
(2)解:∵AB是☉O的直径,☉O的半径为,
∴∠ACB=90°,OC=OB=,AB=2.
∵∠A=∠BDC,
∴=tan A=tan∠BDC=,
∴AC=2BC,
∴AB===BC=2,
∴BC=2.
∵∠FCB+∠OCB=90°,∠A+∠ABC=90°,
且∠OCB=∠ABC,
∴∠FCB=∠A=∠BDC,
∴=tan∠FCB=tan∠BDC==,
∴CF=2BF,
∴BC===BF=2,
∴BF=,
∴DF=2CF=4BF=4×=,
∴BD=DF-BF=-=.
∵OC∥DB,
∴△OCE∽△BDE,
∴===,
∴OE=OB=×=,
∴线段OE的长是.
4.D
5.B 解析:选项A,如图1,设三角形的内心为O,分别过点O作三边的垂线,垂足为D,E,F,连接OA,OB,OC,
∴OD=OE=OF=r,
∴S△ABC=S△AOB+S△BOC+S△AOC=OF·AB+OD·BC+OE·AC=r(AB+BC+AC).∴三角形内切圆半径r=.∵三角形是等边三角形,
∴S=×82=16,
∴三角形内切圆半径rA===;选项B,如图2,△ABC中,AB=AC=10,BC=4,过A作AD⊥BC于D,
∴CD=BC=2,
∴AD===4,
∴S△ABC=AD·BC=×4×4=8,
∴三角形内切圆半径rB===;选项C,如图3,△ABC中,AB=10,AC=9,BC=5,过点A作AD⊥BC于点D,设CD=x,则BD=5-x,∵AD2=AB2-BD2=AC2-CD2,
∴AD2=102-(5-x)2=92-x2,解得x=,AD==,
∴S△ABC=AD·BC=×5×=6,
∴三角形内切圆半径rC===;选项D,△ABC中,AB=10,AC=8,BC=6,
∴AB2=100=AC2+BC2,
∴△ABC是直角三角形,
∴S△ABC=AC·BC=×8×6=24,
∴三角形内切圆半径rD===2.∵<<2<,
∴内切圆半径最小的是4,10,10.故选B.
图1 图2 图3
6.解:(1)如图1,外接圆的圆心为O,连接OA,OB,∵O是等腰三角形的外心,AB=AC,
∴∠BAO=∠OAC=∠BAC=×120°=60°.∵OA=OB,
∴△AOB是等边三角形,
∴OB=AB=5,故△ABC外接圆半径R的长为5.
(2)如图2所示,连接MO并延长交☉O于点N,连接OP,显然MP≤OM+OP=OM+ON=MN.∵AB=24,M是AB的中点,
∴MN⊥AB,AM=MB=12.∵ON=13,
∴OM===5.∴MN=18,
∴PM的最大值为18.
(3)如图3所示,假设P点即为所求点,分别作出点P关于AB,AC的对称点P',P″,连接PP',P'E,PE,PF,PP″,由对称性可知PE+EF+FP=P'E+EF+FP″=P'P″,且P',E,F,P″在一条直线上,所以P'P″即为最短距离,其长度取决于PA的长度, 如图④,作出的圆心O,连接AO,与弧BC交于点P,P点即为使得PA最短的点,∵AB=6 km,AC=3 km,∠BAC=60°,
∴△ABC是直角三角形,∠ABC=30°,BC=3,所对的圆心角为60°,
∴△OBC是等边三角形,∠CBO=60°,BO=BC=3,
∴∠ABO=90°,AO==3,PA=3-3,∠P'AE=∠EAP,∠PAF=∠FAP″,
∴∠P'AP″=2∠ABC=120°,P'A=AP″,
∴∠AP'E=∠AP″F=30°,∵P'P″=2P'Acos ∠AP'E=P'A=3-9,
∴PE+EF+FP的最小值为(3-9)km.
7.3+2 解析:如图,延长AO交BC于点E,延长CB到点F,使BF=BC.∵BF=BC,
∴B是CF的中点.∵D 为线段 CO'的中点,
∴BD是△CF O'的中位线,
∴BD=F O'.∵线段 AO绕点A逆时针旋转至O',
∴点O'在以点A为圆心,AO为半径的圆上运动.如图,当点F,O',A在同一条直线上时,FO'最长,BD=F O'最大.∵点O是△ABC的重心,
∴AE是△ABC的中线,
∴BE=CE=BC=8.∵AB=AC,
∴△ABC是等腰三角形,
∴AE⊥BC,
∴∠AEB=90°.∵AB=10,
∴AE===6.∵O为△ABC的重心,
∴AO=AE=4.∵BF=BC=16,BE=8,
∴EF=BE+BF=24,
∴AF===6.由旋转的性质知AO'=AO=4,
∴FO'=FA+AO'=6+4,
∴BD=FO'=(6+4)=3+2,即BD 的最大值为3+2,故答案为3+2.
8.解:(1)如图,连接AC,∵AB是☉O的直径,
∴∠ACB=90°.在Rt△ABC中,AB=10,BC=2,
∴AC==4,
∴tan ∠BPC=tan ∠BAC==.
(2)的值不会发生变化,理由如下:∵∠PCD=∠ACB=90°,
∴∠1+∠PCB=∠2+∠PCB,
∴∠1=∠2.∵∠3是圆内接四边形APBC的一个外角,
∴∠3=∠PAC,
∴△CBD∽△CAP,
∴=.在Rt△PCD中,=tan∠BPC=,
∴==.
(3)由(2)知BD=AP,
∴AP+2BP=2=2(BD+BP)=2PD=.由tan∠BPC=,得cos∠BPC=,
∴AP+2BP=PC≤AB=10,
∴AP+2BP的最大值为10.
9.解:(1)∵∠APC=∠CPB=60°,
∴,对应的圆周角为60°,
∴∠ABC=60°,∠BAC=60°,
∴∠ACB=180°-60°-60°=60°,
∴△ABC为等边三角形.故答案为等边.
(2)PC=PA+PB.理由:如图1,在PC上截取PD=AP,连接AD,∵∠APC=60°,
∴△APD为等边三角形,
∴AD=AP=PD,∠ADP=60°,∠ADC=120°.∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB.在△APB和△ADC中,∴△APB≌△ADC(AAS),
∴BP=CD.∵PD=AP,
∴PC=PA+PB.
解:(3)如图2,根据题意可知,M的轨迹是以OC为直径的圆,设圆心为O',连接BO',过点O'作O'N⊥BC于点N,过点O作OQ⊥BC于点Q,
∴∠O'CB=30°,O'C=,
∴O'N=,CN=,
∴O'N∥OQ.∵O'是OC的中点,
∴O'N是三角形OQC的中位线,
∴N为CQ的中点,
∴CQ=2CN=.又∵Q是BC的中点,
∴BC=2CQ=,
∴BN=BC-CN=-=,
∴BO'===,
∴BM最小=BO'-O'M=-.
图1 图2
