2025年人教A版高一数学暑假作业13:高一综合(5)(含解析)
文档属性
| 名称 | 2025年人教A版高一数学暑假作业13:高一综合(5)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-03 10:27:15 | ||
图片预览




文档简介
人教A版高一暑假作业13:高一综合(5)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.(2025·宁夏回族自治区·期中考试)下列命题中正确的是( )
A. 三点确定一个平面
B. 两两相交且不共点的三条直线确定一个平面
C. 圆的一条直径与圆上一点可确定一个平面
D. 四边形可确定一个平面
2.(2025·全国·模拟题)已知,则( )
A. B. C. D.
3.(2024·四川省攀枝花市·期末考试)某中学高一、高二、高三年级的学生分别为人、人、人,为了解不同年级学生身体素质情况,现用比例分配的分层随机抽样的方法从高三年级抽取了人,则其他年级应该抽取的学生人数为( )
A. B. C. D.
4.(2025·广东省·单元测试)已知是单位向量,,若在方向上的投影向量是,则与的夹角为( )
A. B. C. D.
5.(2024·四川省攀枝花市·期末考试)已知、是两条不同的直线,、是两个不同的平面,下列说法正确的是( )
A. 若,,则 B. 若,,则.
C. 若,,,则 D. 若,,,则
6.(2025·浙江省·月考试卷)已知随机事件,,中,与相互独立,与对立,且,,则( )
A. B. C. D.
7.(2025·广东省·月考试卷)已知四面体的外接球的球心在上,且平面,,若四面体的体积为,求球的表面积( )
A. B. C. D.
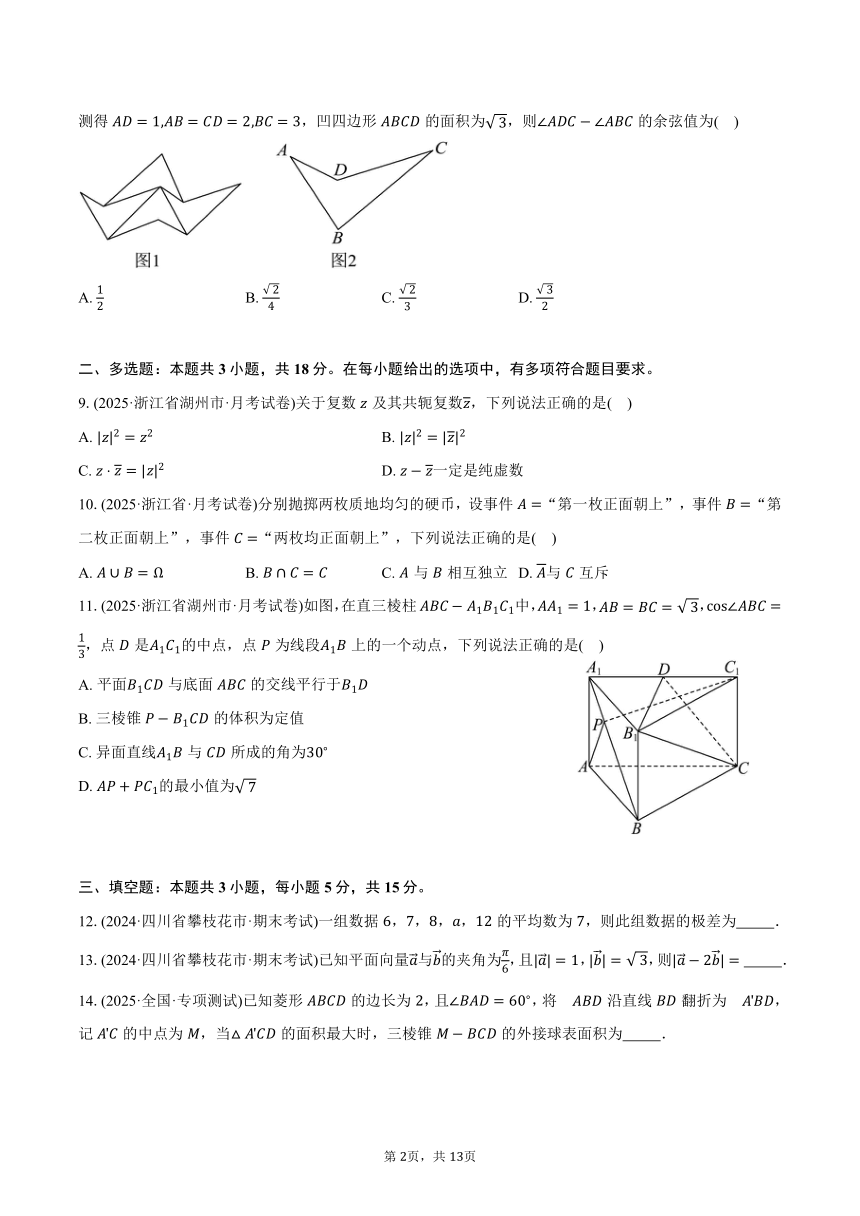
8.(2025·湖南省长沙市·模拟题)密铺,即平面图形的镶嵌,用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.皇冠图形图是一个密铺图形,它由四个完全相同的平面凹四边形组成.在平面凹四边形图中,测得,凹四边形的面积为,则的余弦值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.(2025·浙江省湖州市·月考试卷)关于复数及其共轭复数,下列说法正确的是( )
A. B.
C. D. 一定是纯虚数
10.(2025·浙江省·月考试卷)分别抛掷两枚质地均匀的硬币,设事件“第一枚正面朝上”,事件“第二枚正面朝上”,事件“两枚均正面朝上”,下列说法正确的是( )
A. B. C. 与相互独立 D. 与互斥
11.(2025·浙江省湖州市·月考试卷)如图,在直三棱柱中,,,,点是的中点,点为线段上的一个动点,下列说法正确的是( )
A. 平面与底面的交线平行于
B. 三棱锥的体积为定值
C. 异面直线与所成的角为
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.(2024·四川省攀枝花市·期末考试)一组数据,,,,的平均数为,则此组数据的极差为 .
13.(2024·四川省攀枝花市·期末考试)已知平面向量与的夹角为,且,,则 .
14.(2025·全国·专项测试)已知菱形的边长为,且,将沿直线翻折为,记的中点为,当的面积最大时,三棱锥的外接球表面积为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(2025·福建省厦门市·月考试卷)本小题分
已知点,,.
若,,三点共线,求;
若,求.
16.(2024·四川省攀枝花市·期末考试)本小题分
袋中有个大小相同颜色不全相同的小球,分别为黑球、黄球、绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
从中任取一球,得到黑球.黄球.绿球的概率各是多少?
从中任取两个球,得到的两个球颜色不相同的概率是多少?
17.(2025·湖北省武汉市·月考试卷)本小题分
已知锐角的内角所对的边分别,且若,,且.
求角和边.
若点满足,求的面积.
18.(2025·浙江省·月考试卷)本小题分
文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创建者,某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均不低于分分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值,并求样本成绩的第百分位数;
现从以上各段中采用样本量比例分配的分层随机抽样再抽取份答卷作为“典型答卷”进一步统计研究,若落在的“典型答卷”的平均成绩与方差分别是和,落在的“典型答卷”的平均成绩与方差分别是和,据此估计这份答卷中落在的所有答卷的成绩的方差.
19.(2025·湖南省·单元测试)本小题分
如图,在四棱锥中,底面为直角梯形,且,,侧面底面若.
求证:平面;
侧棱上是否存在点,使得平面若存在,指出点的位置并证明,若不存在,请说明理由;
求二面角的余弦值.
1.【答案】
【解析】解:由确定平面的依据可知,不共线的三点确定一个平面,故错误;
B.两两相交且不共点的三条直线确定一个平面,故正确;
C.根据确定平面的依据,直线和直线外一点确定一个平面,所以应改为圆的一条直径和圆上除直径端点外的一点,可确定一个平面,故错误;
D.空间四边形,四点不在同一个平面,故错误;
故选B.
2.【答案】
【解析】解:因为,
所以.
故选:.
3.【答案】
【解析】解:设三个年级共抽取人,则由题意得
,解得,
所以其他年级应该抽取的学生人数为.
故选:
4.【答案】
【解析】解:因为在方向上的投影向量是,
所以,
所以,又,所以.
故选D.
5.【答案】
【解析】解:对于,如图,当,时,,所以 A错误,
对于,如图,当,时,,所以 B错误,
对于,如图,当,,时,是异面直线,所以 C错误,
对于,因为,,所以或,
当时,因为,所以,
当时,过直线作平面,,则,
因为,所以,
因为,所以,
综上,,所以 D正确.
故选:
6.【答案】
【解析】解:,,
所以.
故选B.
7.【答案】
【解析】解:如图所示,
四面体的外接球的球心在上,平面,
所在的圆是大圆,为球半径.
,,,
又,,
四面体 的体积为:
,
,球的表面积,
故选B.
8.【答案】
【解析】解:如图,连接,
因为,
在中,由余弦定理得,
则,
在中,由余弦定理得,
则,
所以,
即,
因为,
,
所以,
则式和式分别平方并相加得:
,
则,所以,
即的余弦值为.
故选:.
9.【答案】
【解析】解:对于,设,则,故 A错误;
对于,设,则,从而,故 B正确;
对于,设,则,从而,故 C正确;
对于,设,则,从而,当时,是实数,故 D错误.
故选BC.
10.【答案】
【解析】解:正,正,正,反,反,正,反,反,正,正,正,反,正,正,反,正,正,正,
对于,正,正,正,反,反,正,, A错误;
对于,正,正,, B正确;
对于,正,正,,
,所以与相互独立, C正确;
对于,反,正,反,反,与不可能同时发生,因此与互斥, D正确.
故选:
11.【答案】
【解析】解:对于,设平面与底面的交线为,因为平面平面,
平面平面,所以,所以 A正确,
对于,连接交于点,连接,因为四边形为矩形,
所以为的中点,
因为点是的中点,所以,
因为平面,平面,所以平面,
因为点为线段上的一个动点,所以点到平面的距离为定值,
因为的面积也为定值,所以三棱锥的体积为定值,所以 B正确,
对于,由选项B可知,所以异面直线与所成的角,
因为,,
所以,
所以,所以,
,则,,
所以,所以为等腰直角三角形,所以,
所以异面直线与所成的角为,所以 C错误,
对于,由选项C可知,则为等边三角形,
如图,将平面和平面展在同一个平面内,则的最小值为,
在中,,则,
所以,所以,
所以的最小值为,所以 D正确,
故选:
12.【答案】
【解析】解:一组数据,,,,的平均数为,解得,
所以此组数据的极差为.故答案为.
13.【答案】
【解析】解:向量与的夹角为,且,,则,
所以.
故答案为.
14.【答案】
【解析】解:根据题意可知,如下图所示:
当的面积最大时,即取得最大值,
可得,
由对称性可知,可得;
又因为为的中点,所以,
又,由勾股定理可知棱两两垂直,
则可将三棱锥补形成以、、为一个顶点出发的三条棱的正方体,
其外接球与正方体外接球相同,
所以三棱锥的外接球半径为,
可得该外接球的表面积,
故答案为:.
15.【答案】解:因为点,,,
则,,
由,,三点共线,得,
则,解得,即,
所以.
因为点,,,
则,,
,
由,得,
解得,所以,
故.
16.【答案】解:从中任取一球,分别记得到黑球、黄球、绿球为事件,,,
由于,,为互斥事件,
根据已知得解得
从中任取一球,得到黑球、黄球、绿球的概率分别是;
由知黑球、黄球、绿球个数分别为,,,
得到的两个球同色的可能有:两个黑球只有种情况,两个绿球共种情况,
而从个球中取出个球的情况共有种,
所以两个球同色的概率为:,
则得到的两个球颜色不相同的概率是:.
17.【答案】解:由,得
即,
由正弦定理,
,
又,
又.
由,
代入得,
或,
当时,,不合题意,舍去;
当时,,符合题意,
所以;
,
,
在上,且为靠近的三等分点,
,
.
18.【答案】解:由频率分布直方图各小矩形的面积之和为,
得,所以;
成绩落在内的 频率为,
落在内的频率为,
则第百分位数,,解得,
所以第百分位数为.
依题意,抽取份答卷中,落在内的有份,落在内的有份,
落在的“典型答卷”的平均成绩,
落在的“典型答卷”的方差,
所以估计这份答卷中落在的所有答卷的成绩的方差为.
19.【答案】解:因为,
所以.又因为侧面底面,且侧面底面,
所以底面.而底面,所以.
在底面中,因为,,
所以,所以.又因为,,
所以平面
在上存在中点,使得平面,
证明如下:设的中点是,连结,,,
则,且.
由已知,
所以,又,
所以,且,
所以四边形为平行四边形,所以.
因为平面,平面,
所以平面
设为中点,连结,则.
又因为平面平面,侧面底面,,
所以平面.
又,故,
过作于,连结,
由,,
故,
又,
故.
所以是二面角的平面角.
设,则, .
在中,,所以.
所以 ,.
即二面角的余弦值为
第2页,共2页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.(2025·宁夏回族自治区·期中考试)下列命题中正确的是( )
A. 三点确定一个平面
B. 两两相交且不共点的三条直线确定一个平面
C. 圆的一条直径与圆上一点可确定一个平面
D. 四边形可确定一个平面
2.(2025·全国·模拟题)已知,则( )
A. B. C. D.
3.(2024·四川省攀枝花市·期末考试)某中学高一、高二、高三年级的学生分别为人、人、人,为了解不同年级学生身体素质情况,现用比例分配的分层随机抽样的方法从高三年级抽取了人,则其他年级应该抽取的学生人数为( )
A. B. C. D.
4.(2025·广东省·单元测试)已知是单位向量,,若在方向上的投影向量是,则与的夹角为( )
A. B. C. D.
5.(2024·四川省攀枝花市·期末考试)已知、是两条不同的直线,、是两个不同的平面,下列说法正确的是( )
A. 若,,则 B. 若,,则.
C. 若,,,则 D. 若,,,则
6.(2025·浙江省·月考试卷)已知随机事件,,中,与相互独立,与对立,且,,则( )
A. B. C. D.
7.(2025·广东省·月考试卷)已知四面体的外接球的球心在上,且平面,,若四面体的体积为,求球的表面积( )
A. B. C. D.
8.(2025·湖南省长沙市·模拟题)密铺,即平面图形的镶嵌,用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.皇冠图形图是一个密铺图形,它由四个完全相同的平面凹四边形组成.在平面凹四边形图中,测得,凹四边形的面积为,则的余弦值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.(2025·浙江省湖州市·月考试卷)关于复数及其共轭复数,下列说法正确的是( )
A. B.
C. D. 一定是纯虚数
10.(2025·浙江省·月考试卷)分别抛掷两枚质地均匀的硬币,设事件“第一枚正面朝上”,事件“第二枚正面朝上”,事件“两枚均正面朝上”,下列说法正确的是( )
A. B. C. 与相互独立 D. 与互斥
11.(2025·浙江省湖州市·月考试卷)如图,在直三棱柱中,,,,点是的中点,点为线段上的一个动点,下列说法正确的是( )
A. 平面与底面的交线平行于
B. 三棱锥的体积为定值
C. 异面直线与所成的角为
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.(2024·四川省攀枝花市·期末考试)一组数据,,,,的平均数为,则此组数据的极差为 .
13.(2024·四川省攀枝花市·期末考试)已知平面向量与的夹角为,且,,则 .
14.(2025·全国·专项测试)已知菱形的边长为,且,将沿直线翻折为,记的中点为,当的面积最大时,三棱锥的外接球表面积为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(2025·福建省厦门市·月考试卷)本小题分
已知点,,.
若,,三点共线,求;
若,求.
16.(2024·四川省攀枝花市·期末考试)本小题分
袋中有个大小相同颜色不全相同的小球,分别为黑球、黄球、绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
从中任取一球,得到黑球.黄球.绿球的概率各是多少?
从中任取两个球,得到的两个球颜色不相同的概率是多少?
17.(2025·湖北省武汉市·月考试卷)本小题分
已知锐角的内角所对的边分别,且若,,且.
求角和边.
若点满足,求的面积.
18.(2025·浙江省·月考试卷)本小题分
文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创建者,某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均不低于分分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值,并求样本成绩的第百分位数;
现从以上各段中采用样本量比例分配的分层随机抽样再抽取份答卷作为“典型答卷”进一步统计研究,若落在的“典型答卷”的平均成绩与方差分别是和,落在的“典型答卷”的平均成绩与方差分别是和,据此估计这份答卷中落在的所有答卷的成绩的方差.
19.(2025·湖南省·单元测试)本小题分
如图,在四棱锥中,底面为直角梯形,且,,侧面底面若.
求证:平面;
侧棱上是否存在点,使得平面若存在,指出点的位置并证明,若不存在,请说明理由;
求二面角的余弦值.
1.【答案】
【解析】解:由确定平面的依据可知,不共线的三点确定一个平面,故错误;
B.两两相交且不共点的三条直线确定一个平面,故正确;
C.根据确定平面的依据,直线和直线外一点确定一个平面,所以应改为圆的一条直径和圆上除直径端点外的一点,可确定一个平面,故错误;
D.空间四边形,四点不在同一个平面,故错误;
故选B.
2.【答案】
【解析】解:因为,
所以.
故选:.
3.【答案】
【解析】解:设三个年级共抽取人,则由题意得
,解得,
所以其他年级应该抽取的学生人数为.
故选:
4.【答案】
【解析】解:因为在方向上的投影向量是,
所以,
所以,又,所以.
故选D.
5.【答案】
【解析】解:对于,如图,当,时,,所以 A错误,
对于,如图,当,时,,所以 B错误,
对于,如图,当,,时,是异面直线,所以 C错误,
对于,因为,,所以或,
当时,因为,所以,
当时,过直线作平面,,则,
因为,所以,
因为,所以,
综上,,所以 D正确.
故选:
6.【答案】
【解析】解:,,
所以.
故选B.
7.【答案】
【解析】解:如图所示,
四面体的外接球的球心在上,平面,
所在的圆是大圆,为球半径.
,,,
又,,
四面体 的体积为:
,
,球的表面积,
故选B.
8.【答案】
【解析】解:如图,连接,
因为,
在中,由余弦定理得,
则,
在中,由余弦定理得,
则,
所以,
即,
因为,
,
所以,
则式和式分别平方并相加得:
,
则,所以,
即的余弦值为.
故选:.
9.【答案】
【解析】解:对于,设,则,故 A错误;
对于,设,则,从而,故 B正确;
对于,设,则,从而,故 C正确;
对于,设,则,从而,当时,是实数,故 D错误.
故选BC.
10.【答案】
【解析】解:正,正,正,反,反,正,反,反,正,正,正,反,正,正,反,正,正,正,
对于,正,正,正,反,反,正,, A错误;
对于,正,正,, B正确;
对于,正,正,,
,所以与相互独立, C正确;
对于,反,正,反,反,与不可能同时发生,因此与互斥, D正确.
故选:
11.【答案】
【解析】解:对于,设平面与底面的交线为,因为平面平面,
平面平面,所以,所以 A正确,
对于,连接交于点,连接,因为四边形为矩形,
所以为的中点,
因为点是的中点,所以,
因为平面,平面,所以平面,
因为点为线段上的一个动点,所以点到平面的距离为定值,
因为的面积也为定值,所以三棱锥的体积为定值,所以 B正确,
对于,由选项B可知,所以异面直线与所成的角,
因为,,
所以,
所以,所以,
,则,,
所以,所以为等腰直角三角形,所以,
所以异面直线与所成的角为,所以 C错误,
对于,由选项C可知,则为等边三角形,
如图,将平面和平面展在同一个平面内,则的最小值为,
在中,,则,
所以,所以,
所以的最小值为,所以 D正确,
故选:
12.【答案】
【解析】解:一组数据,,,,的平均数为,解得,
所以此组数据的极差为.故答案为.
13.【答案】
【解析】解:向量与的夹角为,且,,则,
所以.
故答案为.
14.【答案】
【解析】解:根据题意可知,如下图所示:
当的面积最大时,即取得最大值,
可得,
由对称性可知,可得;
又因为为的中点,所以,
又,由勾股定理可知棱两两垂直,
则可将三棱锥补形成以、、为一个顶点出发的三条棱的正方体,
其外接球与正方体外接球相同,
所以三棱锥的外接球半径为,
可得该外接球的表面积,
故答案为:.
15.【答案】解:因为点,,,
则,,
由,,三点共线,得,
则,解得,即,
所以.
因为点,,,
则,,
,
由,得,
解得,所以,
故.
16.【答案】解:从中任取一球,分别记得到黑球、黄球、绿球为事件,,,
由于,,为互斥事件,
根据已知得解得
从中任取一球,得到黑球、黄球、绿球的概率分别是;
由知黑球、黄球、绿球个数分别为,,,
得到的两个球同色的可能有:两个黑球只有种情况,两个绿球共种情况,
而从个球中取出个球的情况共有种,
所以两个球同色的概率为:,
则得到的两个球颜色不相同的概率是:.
17.【答案】解:由,得
即,
由正弦定理,
,
又,
又.
由,
代入得,
或,
当时,,不合题意,舍去;
当时,,符合题意,
所以;
,
,
在上,且为靠近的三等分点,
,
.
18.【答案】解:由频率分布直方图各小矩形的面积之和为,
得,所以;
成绩落在内的 频率为,
落在内的频率为,
则第百分位数,,解得,
所以第百分位数为.
依题意,抽取份答卷中,落在内的有份,落在内的有份,
落在的“典型答卷”的平均成绩,
落在的“典型答卷”的方差,
所以估计这份答卷中落在的所有答卷的成绩的方差为.
19.【答案】解:因为,
所以.又因为侧面底面,且侧面底面,
所以底面.而底面,所以.
在底面中,因为,,
所以,所以.又因为,,
所以平面
在上存在中点,使得平面,
证明如下:设的中点是,连结,,,
则,且.
由已知,
所以,又,
所以,且,
所以四边形为平行四边形,所以.
因为平面,平面,
所以平面
设为中点,连结,则.
又因为平面平面,侧面底面,,
所以平面.
又,故,
过作于,连结,
由,,
故,
又,
故.
所以是二面角的平面角.
设,则, .
在中,,所以.
所以 ,.
即二面角的余弦值为
第2页,共2页
同课章节目录
