(单元培优卷)第7单元 解决问题的策略 单元全真模拟培优卷(含解析)-2025-2026学年五年级上册数学(苏教版)
文档属性
| 名称 | (单元培优卷)第7单元 解决问题的策略 单元全真模拟培优卷(含解析)-2025-2026学年五年级上册数学(苏教版) |  | |
| 格式 | docx | ||
| 文件大小 | 109.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-03 14:59:34 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年五年级上册数学单元全真模拟培优卷(苏教版)
第7单元 解决问题的策略
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.一根铁丝长18厘米,用这根铁丝围成一个等腰三角形,并使围成的三角形的边长是整厘米数,能围成( )种不同的等腰三角形?
A.3 B.4 C.5 D.6
2.用12根同样长的木棍围一个长方形或正方形,有( )种不同的围法。
A.6 B.5 C.4 D.3
3.一辆长途汽车往返于A、B两地,沿途要经过C、D二个站.汽车运输公司要为这辆汽车准备( )种车票.
A.4 B.12 C.6
4.舞蹈演员在舞台上排成5条直线,每条直线上有4名演员,则最少需要舞蹈演员( )
A.10名 B.12名 C.16名 D.20名
5.动物园学生门票每张10元,小林有两张5元,五张2元,两张1元的纸币.小红一共有( )种不同的付钱方法.
A.3 B.4 C.5 D.6
6.一根铁丝长18厘米,把它围成长和宽都是整厘米数的长方形,围成的长方形面积最大是( )平方厘米.
A.8 B.14 C.18 D.20
7.有10克、20克和50克的砝码各一个,用其中的1个、2个或3个,放在天平的一端,能称出( )不同的质量.
A.3种 B.6种 C.7种 D.8种
8.一个两位数,如果将它十位上的数和个位上的数对调,那么得到的数比原来大18。这样的数有( )个。
A.6 B.7 C.8 D.9
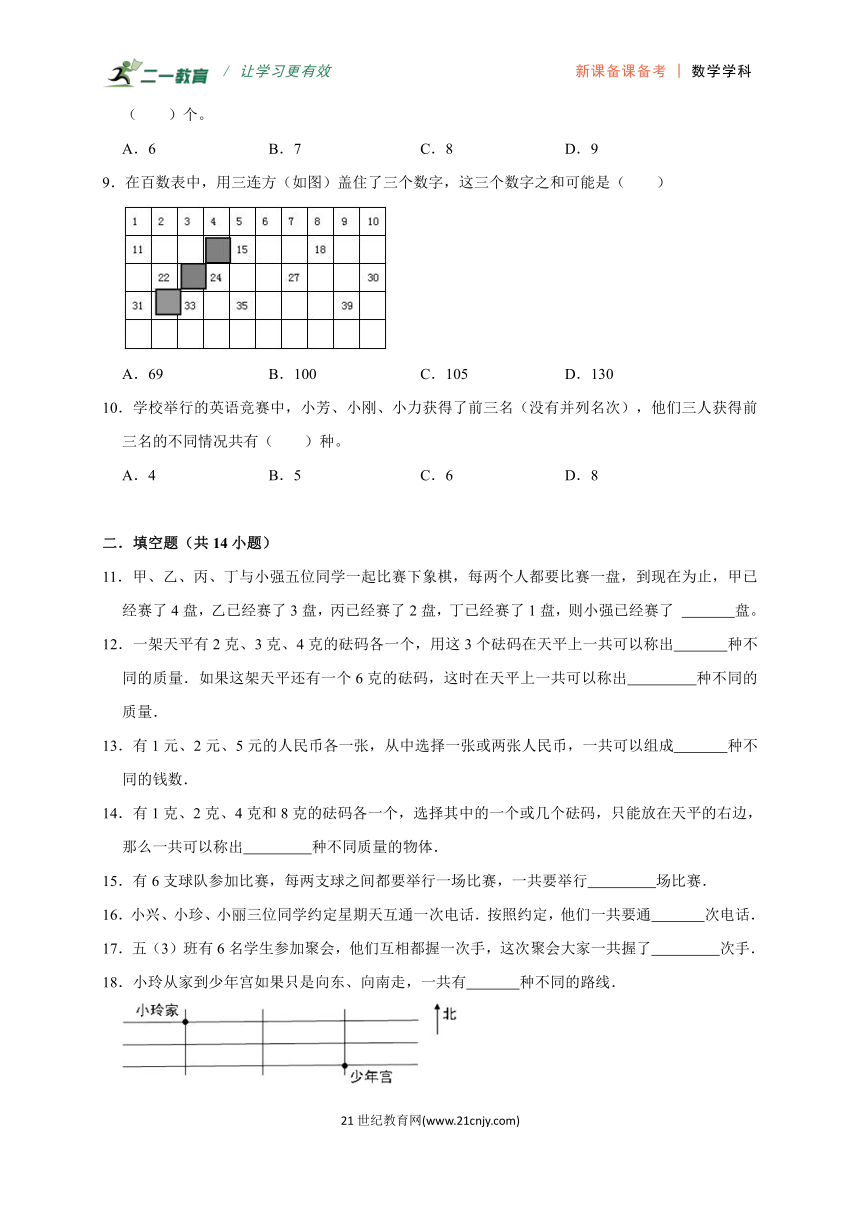
9.在百数表中,用三连方(如图)盖住了三个数字,这三个数字之和可能是( )
A.69 B.100 C.105 D.130
10.学校举行的英语竞赛中,小芳、小刚、小力获得了前三名(没有并列名次),他们三人获得前三名的不同情况共有( )种。
A.4 B.5 C.6 D.8
二.填空题(共14小题)
11.甲、乙、丙、丁与小强五位同学一起比赛下象棋,每两个人都要比赛一盘,到现在为止,甲已经赛了4盘,乙已经赛了3盘,丙已经赛了2盘,丁已经赛了1盘,则小强已经赛了 盘。
12.一架天平有2克、3克、4克的砝码各一个,用这3个砝码在天平上一共可以称出 种不同的质量.如果这架天平还有一个6克的砝码,这时在天平上一共可以称出 种不同的质量.
13.有1元、2元、5元的人民币各一张,从中选择一张或两张人民币,一共可以组成 种不同的钱数.
14.有1克、2克、4克和8克的砝码各一个,选择其中的一个或几个砝码,只能放在天平的右边,那么一共可以称出 种不同质量的物体.
15.有6支球队参加比赛,每两支球之间都要举行一场比赛,一共要举行 场比赛.
16.小兴、小珍、小丽三位同学约定星期天互通一次电话.按照约定,他们一共要通 次电话.
17.五(3)班有6名学生参加聚会,他们互相都握一次手,这次聚会大家一共握了 次手.
18.小玲从家到少年宫如果只是向东、向南走,一共有 种不同的路线.
19.小敏的暑假生活是这样安排的:每四天中第一天去图书馆,第二天去少年宫,接着两天去游泳馆。如果7月1日起照此规律活动,小敏第4次去少年宫是7月 日。
20.504路公交车每隔15分钟发一辆。早晨6:00发第1辆,第6辆是 时间发的车,上午10:00发的是第 辆车。
21.小明、小红、小强和小胜四位同学进行五子棋比赛,每两个人都要赛一场.现在小明已经赛了3场,小红赛了2场,小胜赛了1场,小强赛了 场.(可以先画一画再填)
22.小林、小王、小李、小张和小许五位同学一起参加象棋比赛,每两人都要比赛一盘.到现在为止,小林已赛4盘,小王已赛3盘,小李已赛2盘,小张已赛1盘.小许已赛了 盘.
23.用7、9、4三个数字可以组成 个不同的三位数.
24.小红订报纸,有《数学报》、《关心下一代》和《快乐作文》三种供选择,她最少订阅1份,最多订阅3份,有 种不同的订阅方法.
三.判断题(共8小题)
25.从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。 _________
26.用18个1平方厘米的小正方形拼成长方形,有3种不同的拼法。
27.实验小学举行篮球比赛,一共有6支篮球队参加.如果每2支篮球队要赛一场,那么一共要赛10场._____
28.自然博物馆录像厅从上午9时开始每40分钟播放一次录像。现在是上午11时,同学们正好能赶上第三场次的放映。
29.甲、乙、丙、丁4个人参加羽毛球比赛,每2个人比赛一场,一共要比赛8场。
30.把一根木料锯成3段要3.6分钟,锯成5段要6分钟.
31.丽丽借给芳芳2.5元后,两人的钱数一样多,芳芳原来比丽丽少2.5元。
32.将8个相同的小球分成4堆,有2种不同的分法。
四.应用题(共7小题)
33.妈妈为小红准备的早餐是:一块面包、一盒牛奶、一个鸡蛋,小红要把它们吃完,可以有多少种不同顺序的吃法?
34.小文有4张数字卡片2,6,7,9,组成一个一位数和一个三位数相乘,有多少个不同的算式?其中积最大是多少?
35.A、B、C、D、E五位同学进行乒乓球循环赛(其中任何一位同学都必须和其他每一位同学进行一场比赛),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场。你能想办法知道E赛了多少场?
36.念念是一个爱读书的学生,他在学校图书馆中看到四本学习杂志:《数学世界》、《数学王国》、《优秀作文》、《英语阅读》。他打算借阅一本到三本。
37.小张、小王、小高、小于、小赵、小李六位同学进行乒乓球比赛,每两人都要赛一场。现在小张和小王已经赛了5场,小高赛了4场,小于和小赵赛了3场,问:小李赛了几场?
38.早餐店供应三种豆浆:草莓豆浆、芝麻豆浆和红枣豆浆,三种点心:煎饼、油条、包子。(先按要求想办法选一选,再回答问题)
(1)小红买两种点心,一共有几种不同的选法?
(2)小亮要买一种豆浆和一种点心,有几种不同的选法?
39.某车站每隔一段相等的时间就到达一辆2路公共汽车。已经知道到站的时刻是8:30、8:38、8:46、8:54,那么如图哪些时刻也是2路车到站的时刻?
参考答案及试题解析
一.选择题(共10小题)
1.【考点】等腰三角形与等边三角形.
【答案】B
【思路分析】要求一共有多少种不同围法,需先求符合条件的腰和底有多少种,依据三角形的周长公式等腰三角形的“周长=腰×2+底”以及“底和腰都是整厘米数”就可以进行计算。
【解答】解:周长=腰×2+底
18÷3=6(厘米)
则等腰三角形可以是以下几种:
①5厘米,5厘米,8厘米;
②6厘米,6厘米,6厘米;
③7厘米,7厘米,4厘米;
④8厘米,8厘米,2厘米;
答:能围成4种不同的等腰三角形。
故选:B。
【名师点评】此题主要依据三角形的周长的意义,以及三角形的三条边的关系,解决问题。
2.【考点】长方形的周长.
【答案】D
【思路分析】根据长方形的周长公式:C=(a+b)×2,那么a+b=C÷2,据此求出长与宽的和,进而确定有几种不同的围法。
【解答】解:12÷2=6
6=5+1=4+2=3+3
可以围成长是5、宽是1的长方形,长是4、宽是2的长方形,边长是3的正方形。
答:有3种不同围法。
故选:D。
【名师点评】此题考查的目的是理解掌握长方形、正方形周长的意义及应用。
3.【考点】排列组合.
【答案】B
【思路分析】因为加上两边两个站,一共有4个站,先求出线段条数,一条线段就是一种票价.再考虑往返情况,乘以2就可以.
【解答】解:此题相当于一条线段上有4个点,
有多少种不同的票价即有多少条线段:3+2+1=6(种);
有多少种车票是要考虑顺序的,则有6×2=12(种).
答:一共要准备12种不同的车票.
故选:B.
【名师点评】此题要注意来回的车票种类是不同的,所以要乘上2.
4.【考点】最大与最小.
【答案】A
【思路分析】利用直线两两相交图形,数一数交点的个数即是最少需要舞蹈演员人数,据此解答即可。
【解答】解:如图:,
当5条直线两两相交时,需要的舞蹈演员最少,此时5条直线有10个交点,每一条直线上有4个交点,正好是每排4名演员的位置,所以最少需要舞蹈演员10名。
故选:A。
【名师点评】本题主要考查了最少问题,解题的关键是理解直线两两相交时需要的舞蹈演员最少,利用图形更易理解。
5.【考点】排列组合.
【答案】B
【思路分析】如果含有5元的有:5+5、5+2+2+1,2种;
如果含有2元的有:2+2+2+2+2、2+2+2+2+1+1,2种;
根据加法原理,可得共有:2+2=4(种);据此解答.
【解答】解:含有5元的有:5+5、5+2+2+1,2种;
含有2元的有:2+2+2+2+2、2+2+2+2+1+1,2种;
共有:2+2=4(种);
答:小红一共有4种不同的付钱方法.
故选:B.
【名师点评】本题考查了加法原理即完成一件事情有n类方法,第一类中又有M1种方法,第二类中又有M2种方法,…,第n类中又有 Mn种方法,那么完成这件事情就有M1+M2+…+Mn种方法.
6.【考点】长方形、正方形的面积.
【答案】D
【思路分析】要使围成长方形的面积最大,也就是长和宽的差最小(接近正方形),首先铁丝的长度除以2求出长与宽,进而确定长和宽,然后根据长方形的面积=长×宽,把数据代入公式解答.
【解答】解:18÷2=9(厘米),
则长为5厘米、宽为4厘米时面积最大,
5×4=20(平方厘米),
答:围成长方形的面积最大是20平方厘米.
故选:D.
【名师点评】此题主要考查长方形的周长搜狗、面积公式的灵活运用,关键是熟记公式,明确:长和宽的差最小(接近正方形)面积最大,
7.【考点】筛选与枚举.
【答案】C
【思路分析】分选择1个、2个或者3个砝码,找出其能组合成的所有的质量即可.
【解答】解:(1)每个砝码单独称量时,可以称量出10克、20克、50克三种重量;
(2)三个砝码两两组合称量时,可以称量出:
10+20=30克,
10+50=60克,
20+50=70克,
三种重量;
(3)三个砝码一起称量时,可以称量出:
10+20+50=80克,
3+3+1=7(种),
答:用这三个砝码可以在天平上直接称出7种不同重量的物体.
故选:C.
【名师点评】正确的进行分类,列举出所有的可能即可求解.
8.【考点】数字问题.
【答案】B
【思路分析】设这个数为(a≠0,b≠0),根据题意可得:10b+a﹣10a﹣b=18,整理得b=a+2,然后讨论a、b的取值范围即可得出答案。
【解答】解:设这个数为(a≠0,b≠0),根据题意可得:
10b+a﹣10a﹣b=18
整理得:b=a+2
所以,2<a+2≤9
所以,0<a≤7
所以,a可以是1、2、3、4、5、6、7;对应着b可以是3、4、5、6、7、8、9,
所以,这样的数有7个。
故选:B。
【名师点评】本题考查了数的位置原则,关键是得到十位上的数和个位上的数的等量关系。
9.【考点】百数表.
【答案】A
【思路分析】观察百数表可得:从左边第一列开始,个数数字分别依次是1、2、3、4、5、6、7、8、9、0,据此可得盖住的三个数字从上到下依次是14、23、32,据此把这三个数字加起来即可解答问题.
【解答】解:根据题干分析可得:14+23+32=69
答:这三个数字之和可能是69.
故选:A。
【名师点评】解答此题关键是明确百数表的中数字的排列规律,从而得出盖住的三个数字分别是几,再相加即可.
10.【考点】排列组合.
【答案】C
【思路分析】如果先确定第一名,有3种选择;那么第二名就有2种选择;第三名就有1种选择;然后根据乘法原理,就可求出获得前三名的可能不同的情况,即3×2×1=6种,然后解答即可。
【解答】解:因为没有并列名次,所以可得:
3×2×1=6(种)
答:他们三人获得前三名的情况共有6种。
故选:C。
【名师点评】本题考查了乘法原理,即做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。
二.填空题(共14小题)
11.【考点】逻辑推理.
【答案】2。
【思路分析】甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘,则每位同学都要与其他四位同学各赛一盘,即每人都要赛4盘,已知此时甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;由于丁此时只赛了1盘,则丁这一盘是与甲赛的,与其他人还没有下;乙赛了三 盘,则乙这三盘是与甲、丙、小强赛的;丙赛了2盘,则这两盘是与甲、乙赛的;所以此时小强与甲、乙赛了2盘;据此推理即可。
【解答】解:由于此时甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;
丁此时只赛了1盘,则丁这一盘是与甲赛的,与其他人还没有赛;
乙赛了三 盘,则乙这三盘是与甲、丙、小强赛的;
丙赛了2盘,则这两盘是与甲、乙赛的;
所以此时小强赛了2盘,是与甲、乙赛的。
答:小强已经赛了2盘。
故答案为:2。
【名师点评】根据每人需要赛的总盘数及此时每人已赛的盘数进行分析推理是完成此类问题的关键。
12.【考点】筛选与枚举.
【答案】见试题解答内容
【思路分析】(1)先选原先单个的砝码,有3种不同的质量,再两个搭配,得出不同的质量,最后三个搭配得出不同的质量;
(2)类比(1)的方法,一一列举解决问题.
【解答】解:(1)一个砝码:2克,3克,4克共3种不同的质量,
两个砝码搭配:2克+3克=5克,2克+4克=6克,3克+4克=7克,共3种不同的质量,
三个搭配:2克+3克+4克=9克,
共有:3+3+1=7(种);
(2)一个砝码:2克,3克,4克,6克共4种不同的质量,
两个砝码搭配:2克+3克=5克,2克+4克=6克,3克+4克=7克,2克+6克=8克,3克+6克=9克,4克+6克=10克,共6种不同的质量,
三个搭配:2克+3克+4克=9克,2克+3克+6克=11克,6克+3克+4克=13克,2克+4克+6克=12克,
四个搭配:2克+3克+4克+6克=15克有1种不同的质量,
去掉2种重复的质量;
共有:4+6+4+1﹣2=13(种);
故答案为:7;13.
【名师点评】利用列举法注意分类的标准,一一列举做到不重不漏.
13.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】当取出1张人民币时,可以组成3种不同的钱数;当取出2张人民币时可以组成3种不同的钱数,由此得出答案.
【解答】解:当取出1张人民币时,可以组成1元、2元、5元,3种不同的钱数;
取出2张人民币时可以组成:1+2=3元、1+5=6元、2+5=7元,3种不同的钱数;
一共可以组成3+3=6种不同的钱数.
故答案为:6.
【名师点评】关键分两种情况分别找出组成的不同的钱数,注意要做到不重复、不遗漏.
14.【考点】筛选与枚举.
【答案】见试题解答内容
【思路分析】4个砝码中选1个有4种:1克、2克、4克、8克;4个砝码中选2个,有6种:3克、5克、9克、6克、10克、12克;4个砝码中选3个,有4种:7克、11克、14克、13克;4个砝码都选出只有一种:15克;四种情况的方法加起来,即可得解.
【解答】解:选1个有4种:1克、2克、4克、8克,
选2个,有6种:3克、5克、9克、6克、10克、12克,
选3个,有4种:7克、11克、14克、13克,
选4个,只有一种:15克;
4+6+4+1=15(种),
答:最多可以称出15种不同重量的物体.
故答案为:15.
【名师点评】此题考查了组合问题,分类解决此类组合问题,用加法原理.
15.【考点】握手问题.
【答案】见试题解答内容
【思路分析】每两个队之间赛一场,那么每个队要赛5场,一共是6×5=30(场),但是甲队与乙队比赛和乙队与甲队比赛是同一场比赛,所以30场比赛就多算了一倍,再除以2即可.
【解答】解:6×(6﹣1)÷2
=6×5÷2
=30÷2
=15(场)
答:一共要举行15场比赛.
故答案为:15.
【名师点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解.
16.【考点】握手问题.
【答案】见试题解答内容
【思路分析】本题属于握手问题,3个小朋友每两人通一次电话,则每个小朋友都要和其他2个人通一次电话,即每个人要打2次电话,共有3个小朋友,所以共打3×2=6次,打电话是在两个人之间进行的,所以他们互通电话共6÷2=3次.
【解答】解:3×2÷2=3(次)
答:一共可以通话3次.
故答案为:3.
【名师点评】本题属于握手问题,根据握手总次数的计算方法来求解,握手次数总和的计算方法:握手次数=人数×(人数﹣1)÷2,握手次数的公式要记住,并灵活运用.
17.【考点】握手问题.
【答案】见试题解答内容
【思路分析】有6名学生参加聚会,每两人握一次手,即每人都要和其他5人握一次手,每人需握5次,共有6人,共握手5×6=30次,握手是在两人之间进行的,去掉重复计算的情况,实际只有30÷2=15次.
【解答】解:6×(6﹣1)÷2
=6×5÷2
=15(次)
答:一共握了15次手.
故答案为:15.
【名师点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人比较多可以用公式:握手次数=人数×(人数﹣1)÷2解答.
18.【考点】排列组合.
【答案】见试题解答内容
【思路分析】根据加法原理,利用“标数法”画图解答即可,注意只许向东或向南行,否则会有重复的情况.
【解答】解:标数法如下:
答:一共有6种不同的路线.
故答案为:6.
【名师点评】解答最短的路线问题,利用“标数法”画图解答是最直观不易出错的最佳方法,特别是复杂的图形;注意一定不要走“回头路”.
19.【考点】简单周期现象中的规律.
【答案】15。
【思路分析】每4天一循环,第四次去少年宫就是第3组循环零2天。据此解答。
【解答】解:3×4+2
=12+2
=14(天)
7月1日+14天=7月15日
答:小敏第4次去少年宫是7月15日。
故答案为:15。
【名师点评】先找到规律,再根据规律求解。
20.【考点】日期和时间的推算.
【答案】7时15分,17。
【思路分析】根据题干,早晨6:00发第一辆,到第六辆车发车,之间有6﹣1=5个间隔时间,即经过了15×5=75分钟,据此用开始发车的时间+经过的时间即可求出第六辆车的发车时间;
用上午10:00减去第一辆车发出的时间,求出经过的时间,再除以15,求出间隔数,加上1即可解答问题。
【解答】解:15×5=75(分钟)
75分钟=1小时15分
6时+1时15分=7时15分
10时﹣6时=4时
4时=240分
240÷15+1
=16+1
=17(辆)
答:第六辆车的发车时间是7时15分,上午10:00发第17辆车。
故答案为:7时15分,17。
【名师点评】考查了日期和时间的推算,本题的难点是求出中间的时间,发车间隔的次数。同时注意单位的换算。
21.【考点】逻辑推理.
【答案】见试题解答内容
【思路分析】由题意,在图上分别标明小明、小红、小强和小胜,根据小明已经赛了3场,小红赛了2场,小胜赛了1场,在图上连线表示出他们比赛的对阵情况,即可得解.
【解答】解:
由图可知,小强赛了2场.
答:小强赛了2场.
故答案为:2.
【名师点评】解答此题要注意小胜赛了1场,是与小明赛的,所以小红赛的两场是与小明和小强.
22.【考点】逻辑推理.
【答案】见试题解答内容
【思路分析】五人进行比赛,每两人都要比赛一盘,则每个人都要每其他4人进行一场比赛,即每人要赛4场:
小林已赛4盘,即小林已和小王、小李、小张、小许各赛一盘;
小王已赛3盘,因为小张只赛过一盘,这一盘是和小林下的.所以小王这三盘是和小林、小李、小许下的;
此时小张二盘已满.
则小许和小林与小王各赛一盘,即已赛了2盘.
【解答】解:由题意可知,每人要进行5﹣1=4场比赛:
小林已赛4盘,小王已赛3盘,小李已赛2盘,小张已赛1盘,
则小林已赛4盘,即小林已和小王、小李、小张、小许各赛一盘;
小张只赛过一盘,这一盘是和小林下的.
所以小王三盘是和小林、小李、小许下的;
此时小张二盘已满.
则小许和小林与小王各赛一盘,即已赛了2盘.
故答案为:2.
【名师点评】根据每人需赛的盘数及已赛的盘数之间的逻辑关系,进行分析排除是完成本题的关键.
23.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】用7、9、4三个数字组成不同的三位数,三个数字填三个空,分步完成,第一步,先填百位数字,有3种可能;第二步,十位数字从剩下的2个中选一个,有2种选法;第三步,剩下的1个数字填在各位,只有1种选法;分步解决用乘法.
【解答】解:3×2×1=6(个);
答:用7、9、4三个数字可以组成6个不同的三位数.
故答案为:6.
【名师点评】此题考查了简单的排列组合,做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2不同的方法,…,做第n步有mn不同的方法.那么完成这件事共有 N=m1m2m3…mn 种不同的方法.
24.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加.
【解答】解:①订阅1种时:可以是任意1种,有3种方法;
②订阅2种时,是从三种中任选2种,共有3种方法;
③订阅3种时就是3份报纸都订阅,有1种方法;
共有:3+3+1=7(种);
答:一共有7种订阅方法.
故答案为:7.
【名师点评】本题分情况讨论后,每一种情况都可以看成简单的组合问题.
三.判断题(共8小题)
25.【考点】三角形边的关系.
【答案】√
【思路分析】根据三角形三条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答即可。
【解答】解:因为2+3=5(厘米)
5厘米大于4厘米
所以用2厘米、3厘米、4厘米三根小棒可以围成一个三角形;
因为3+4=7(厘米)
7厘米大于6厘米
所以用3厘米、4厘米、6厘米三根小棒可以围成一个三角形;
因此,从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。
故答案为:√。
【名师点评】此题考查的目的是理解掌握三角形三条边之间的关系及应用。
26.【考点】图形的拼组.
【答案】√
【思路分析】因18的因数有1,2,3,6,9,18,用18个小正方形拼成的长方形,根据拼成图形的长和宽,求出它们的周长,再进行比较。据此解答。
【解答】解:用18个1平方厘米的小正方形拼成长方形,拼成后长方形的长和宽可分下列情况:
a、长18厘米,宽1厘米,
b、长9厘米,宽2厘米,
c、长6厘米,宽3厘米,
答:一共有3种不同的拼法。原题说法正确。
故答案为:√。
【名师点评】解答本题关键是分情况讨论组成长方形的长和宽。
27.【考点】排列组合;握手问题.
【答案】×
【思路分析】每两个队之间都要赛一场,那么每个队要赛5场,一共是6×5=30(场),但是甲队与乙队比赛和乙队与甲队比赛是同一场比赛,所以30场比赛就多算了一倍,再除以2即可。
【解答】解:6×(6﹣1)÷2
=6×5÷2
=30÷2
=15(场)
即一共要赛15场,所以原题说法错误。
故答案为:×。
【名师点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
28.【考点】日期和时间的推算.
【答案】×
【思路分析】根据经过时间=结束时刻﹣开始时刻,求出上午9时到上午11时经过了多久,再求出里面有几个40分钟,最后加上开始的一次,即可求出上午11时是第几场。
【解答】解:11时﹣9时=2时=120分钟
120÷40+1
=3+1
=4(场)
答:第4场次正好开始放映。
故答案为:×。
【名师点评】解答此题的关键是掌握经过时间=结束时刻﹣开始时刻这个公式。
29.【考点】排列组合.
【答案】×
【思路分析】因为每个人都要与其他3人比赛,所以共要比赛12场,因为比赛是两个人之间进行的,所以重复算了一次,再除以2即可。
【解答】解:4×(4﹣1)÷2
=12÷2
=6(场)
即一共要比赛6场,所以原题说法错误。
故答案为:×。
【名师点评】此类赛制为单循环赛制,比赛场数=参赛人数×(人数﹣1)÷2。
30.【考点】植树问题.
【答案】见试题解答内容
【思路分析】一根木料锯成3段,锯了:3﹣1=2次,共用了3.6分钟,那么锯一次用:3.6÷2=1.8(分);锯成5段,锯了:5﹣1=4次,要用:1.8×4=7.2(分钟);据此解答.
【解答】解:3.6÷(3﹣1)×(5﹣1)
=1.8×4
=7.2(分钟)
即:把它锯成5段要用7.2分钟;所以原题说法错误.
故答案为:×.
【名师点评】本题考查了植树问题,知识点是:锯木次数=段数﹣1.
31.【考点】整数、小数复合应用题.
【答案】×
【思路分析】丽丽借给芳芳2.5元后,丽丽的钱减少了2.5元,而芳芳的钱增加了2.5元,后来他们两人的钱数一样多,说明丽丽比芳芳多2个2.5元,由此求解。
【解答】解:丽丽减少2.5元,芳芳增加2.5元,这时他们的钱数相等,所以原来两人的差是:
2.5×2=5(元)
原题说法是错误的。
故答案为:×。
【名师点评】解决本题关键是知道丽丽减少和芳芳增加是同时的,所以两人相差了2个2.5元,而不是2.5元。
32.【考点】简单的排列、组合;排列组合;筛选与枚举.
【答案】×
【思路分析】将8个相同的小球分成4堆,可以利用列举法解答。
【解答】解:(1,1,1,5)、(1,1,2,4)、(1,1,3,3)、(1、2、2、3)、(2、2、2、2),共有5种不同的分法;所以原题说法错误。
故答案为:×。
【名师点评】解答本题要注意按顺序列举,防止遗漏。
四.应用题(共7小题)
33.【考点】简单的排列、组合;排列组合.
【答案】6种。
【思路分析】第一个吃的有3种选择,第二个吃的有2种选择,第三个吃的有1种选择,然后根据乘法原理解答即可。
【解答】解:3×2×1=6(种)
答:可以有6种不同顺序的吃法。
【名师点评】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
34.【考点】简单的排列、组合;最大与最小;排列组合.
【答案】24;6858。
【思路分析】(1)先排百位有4种选择,再排十位有3种选择,然后排个位有2种选择,最后排一位数有1种选择,然后根据乘法原理解答即可。
(2)根据数位知识及乘法算式的性质可知,乘法算式中的因数越大,积就越大;根据数位知识可知,一个数的高位上数字越大,其值就越大;由此可知,用2、6、7、9这四个数字组成三位数乘一位数的算式,三位数是762,一位数是9;据此解答即可。
【解答】解:(1)4×3×2×1=24(个)
(2)其中积最大是:762×9=6858
答:有24个不同的算式,其中积最大是6858。
【名师点评】本题考查了乘法原理和极值问题,注意:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
35.【考点】逻辑推理.
【答案】两场。
【思路分析】由于共五位同学参赛,进行循环赛,即每个人都要与其它四人赛一场.由题意可知,A赛了4场,则B、C、D、E都与A赛了一场;B赛了3场,则是与A、C、E各赛了一场(由于D只赛了一场已与A赛过);C赛了两场即是与A、B赛的,所以E赛了两场,即是与A、B赛的。
【解答】解:由赛制可知:A赛了4场,则B、C、D、E都与A赛了一场;
B赛了3场,则是与A、C、E各赛了一场(由于D只赛了一场已与A赛过);
C赛了两场即是与A、B赛的,
所以此时E赛了两场,即是与A、B赛的。
答:此时E赛了两场。
【名师点评】根据循环赛的规则与每人比赛的场数之间的逻辑关系推出每人分别与谁进行了比赛是完成本题的关键。
36.【考点】简单的排列、组合;排列组合.
【答案】7种。
【思路分析】根据题意可得:借阅一本有3种方法,借阅两本有3种方法,借阅三本有1种方法,然后根据加法原理解答即可。
【解答】解:3+3+1=7(种)
答:共有7种借阅方法。
【名师点评】用两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析要完成的“一件事”是什么,可以“分类”还是需要“分步”。
37.【考点】逻辑推理.
【答案】2场。
【思路分析】一共有6名同学,每两人都要赛一场,所以每人最多赛5场,根据小张和小王已经赛了5场,可得小张和小王与其余的人都比赛过了,小高赛了4场,去掉和小张、小王的两场比赛,应该和小于、小赵的比赛,小于和小赵赛了3场,这3场就是小张、小王和小高的比赛,六个人只有小李和小张、小王赛过,就是2场比赛,据此解答。
【解答】解:根据分析可知,小张、小王和其余的人都赛过了,小高赛了4场,说明小高和小张、小王、小于、小赵都赛过了;没有和小李赛过;小于和小赵赛了3场,说明小于、小赵与小张、小王、小高赛过了;也没有和小李赛过,小李只和小张、小王赛过;小李只赛过2场。
答:小李只赛了2场。
【名师点评】本题考查逻辑思维推理问题的应用,关键是判断出小张、小王、小高与哪位赛过了。
38.【考点】简单的排列、组合;排列组合.
【答案】(1)3种;(2)9种。
【思路分析】(1)小红买两种点心,即3选2,然后根据握手问题公式“n(n﹣1)÷2”即可求出一共有几种不同的选法。
(2)从3种豆浆中选一种有3种选法,从3种点心中选一种有3种选法,然后根据乘法原理解答即可。
【解答】解:(1)3×(3﹣1)÷2
=6÷2
=3(种)
答:一共有3种不同的选法。
(2)3×3=9(种)
答:小亮要买一种豆浆和一种点心,有9种不同的选法。
【名师点评】(1)本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式 n(n﹣1)÷2解答。
39.【考点】日期和时间的推算;周期性问题.
【答案】9:02,9:42。
【思路分析】由题意得:8时38分﹣8时30分=8分钟,8时46分﹣8时38分=8分钟,8时54分﹣8时46分=8分钟,即每8分钟到站一辆2路公共汽车,由此分别在之后每到站的时刻加上8分钟,然后再进行比较,据此推算即可。
【解答】解:8时38分﹣8时30分=8分钟
8时46分﹣8时38分=8分钟
8时54分﹣8时46分=8分钟
由此可知:每8分钟到站一辆2路公共汽车。
则:8时54分+8分钟=9时2分
9时2分+8分钟=9时10分
9时10分+8分钟=9时18分
9时18分+8分钟=9时26分
9时26分+8分钟=9时34分
9时34分+8分钟=9时42分
9时42分+8分钟=9时50分
9时50分+8分钟=9时58分
9时58分+8分钟=10时6分
10时6分+8分钟=10时14分
10时14分+8分钟=10时22分
10时22分+8分钟=10时30分
10时30分+8分钟=10时38分
10时38分+8分钟=10时46分
10时46分+8分钟=10时54分
10时54分+8分钟=11时2分
由此可得:2路车到站的时刻为9:02,9:42。
答:2路车到站的时刻为9:02,9:42。
【名师点评】此题考查周期性问题。关键在于找到每8分钟到站一辆2路公共汽车。
21世纪教育网(www.21cnjy.com)
2025-2026学年五年级上册数学单元全真模拟培优卷(苏教版)
第7单元 解决问题的策略
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.一根铁丝长18厘米,用这根铁丝围成一个等腰三角形,并使围成的三角形的边长是整厘米数,能围成( )种不同的等腰三角形?
A.3 B.4 C.5 D.6
2.用12根同样长的木棍围一个长方形或正方形,有( )种不同的围法。
A.6 B.5 C.4 D.3
3.一辆长途汽车往返于A、B两地,沿途要经过C、D二个站.汽车运输公司要为这辆汽车准备( )种车票.
A.4 B.12 C.6
4.舞蹈演员在舞台上排成5条直线,每条直线上有4名演员,则最少需要舞蹈演员( )
A.10名 B.12名 C.16名 D.20名
5.动物园学生门票每张10元,小林有两张5元,五张2元,两张1元的纸币.小红一共有( )种不同的付钱方法.
A.3 B.4 C.5 D.6
6.一根铁丝长18厘米,把它围成长和宽都是整厘米数的长方形,围成的长方形面积最大是( )平方厘米.
A.8 B.14 C.18 D.20
7.有10克、20克和50克的砝码各一个,用其中的1个、2个或3个,放在天平的一端,能称出( )不同的质量.
A.3种 B.6种 C.7种 D.8种
8.一个两位数,如果将它十位上的数和个位上的数对调,那么得到的数比原来大18。这样的数有( )个。
A.6 B.7 C.8 D.9
9.在百数表中,用三连方(如图)盖住了三个数字,这三个数字之和可能是( )
A.69 B.100 C.105 D.130
10.学校举行的英语竞赛中,小芳、小刚、小力获得了前三名(没有并列名次),他们三人获得前三名的不同情况共有( )种。
A.4 B.5 C.6 D.8
二.填空题(共14小题)
11.甲、乙、丙、丁与小强五位同学一起比赛下象棋,每两个人都要比赛一盘,到现在为止,甲已经赛了4盘,乙已经赛了3盘,丙已经赛了2盘,丁已经赛了1盘,则小强已经赛了 盘。
12.一架天平有2克、3克、4克的砝码各一个,用这3个砝码在天平上一共可以称出 种不同的质量.如果这架天平还有一个6克的砝码,这时在天平上一共可以称出 种不同的质量.
13.有1元、2元、5元的人民币各一张,从中选择一张或两张人民币,一共可以组成 种不同的钱数.
14.有1克、2克、4克和8克的砝码各一个,选择其中的一个或几个砝码,只能放在天平的右边,那么一共可以称出 种不同质量的物体.
15.有6支球队参加比赛,每两支球之间都要举行一场比赛,一共要举行 场比赛.
16.小兴、小珍、小丽三位同学约定星期天互通一次电话.按照约定,他们一共要通 次电话.
17.五(3)班有6名学生参加聚会,他们互相都握一次手,这次聚会大家一共握了 次手.
18.小玲从家到少年宫如果只是向东、向南走,一共有 种不同的路线.
19.小敏的暑假生活是这样安排的:每四天中第一天去图书馆,第二天去少年宫,接着两天去游泳馆。如果7月1日起照此规律活动,小敏第4次去少年宫是7月 日。
20.504路公交车每隔15分钟发一辆。早晨6:00发第1辆,第6辆是 时间发的车,上午10:00发的是第 辆车。
21.小明、小红、小强和小胜四位同学进行五子棋比赛,每两个人都要赛一场.现在小明已经赛了3场,小红赛了2场,小胜赛了1场,小强赛了 场.(可以先画一画再填)
22.小林、小王、小李、小张和小许五位同学一起参加象棋比赛,每两人都要比赛一盘.到现在为止,小林已赛4盘,小王已赛3盘,小李已赛2盘,小张已赛1盘.小许已赛了 盘.
23.用7、9、4三个数字可以组成 个不同的三位数.
24.小红订报纸,有《数学报》、《关心下一代》和《快乐作文》三种供选择,她最少订阅1份,最多订阅3份,有 种不同的订阅方法.
三.判断题(共8小题)
25.从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。 _________
26.用18个1平方厘米的小正方形拼成长方形,有3种不同的拼法。
27.实验小学举行篮球比赛,一共有6支篮球队参加.如果每2支篮球队要赛一场,那么一共要赛10场._____
28.自然博物馆录像厅从上午9时开始每40分钟播放一次录像。现在是上午11时,同学们正好能赶上第三场次的放映。
29.甲、乙、丙、丁4个人参加羽毛球比赛,每2个人比赛一场,一共要比赛8场。
30.把一根木料锯成3段要3.6分钟,锯成5段要6分钟.
31.丽丽借给芳芳2.5元后,两人的钱数一样多,芳芳原来比丽丽少2.5元。
32.将8个相同的小球分成4堆,有2种不同的分法。
四.应用题(共7小题)
33.妈妈为小红准备的早餐是:一块面包、一盒牛奶、一个鸡蛋,小红要把它们吃完,可以有多少种不同顺序的吃法?
34.小文有4张数字卡片2,6,7,9,组成一个一位数和一个三位数相乘,有多少个不同的算式?其中积最大是多少?
35.A、B、C、D、E五位同学进行乒乓球循环赛(其中任何一位同学都必须和其他每一位同学进行一场比赛),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场。你能想办法知道E赛了多少场?
36.念念是一个爱读书的学生,他在学校图书馆中看到四本学习杂志:《数学世界》、《数学王国》、《优秀作文》、《英语阅读》。他打算借阅一本到三本。
37.小张、小王、小高、小于、小赵、小李六位同学进行乒乓球比赛,每两人都要赛一场。现在小张和小王已经赛了5场,小高赛了4场,小于和小赵赛了3场,问:小李赛了几场?
38.早餐店供应三种豆浆:草莓豆浆、芝麻豆浆和红枣豆浆,三种点心:煎饼、油条、包子。(先按要求想办法选一选,再回答问题)
(1)小红买两种点心,一共有几种不同的选法?
(2)小亮要买一种豆浆和一种点心,有几种不同的选法?
39.某车站每隔一段相等的时间就到达一辆2路公共汽车。已经知道到站的时刻是8:30、8:38、8:46、8:54,那么如图哪些时刻也是2路车到站的时刻?
参考答案及试题解析
一.选择题(共10小题)
1.【考点】等腰三角形与等边三角形.
【答案】B
【思路分析】要求一共有多少种不同围法,需先求符合条件的腰和底有多少种,依据三角形的周长公式等腰三角形的“周长=腰×2+底”以及“底和腰都是整厘米数”就可以进行计算。
【解答】解:周长=腰×2+底
18÷3=6(厘米)
则等腰三角形可以是以下几种:
①5厘米,5厘米,8厘米;
②6厘米,6厘米,6厘米;
③7厘米,7厘米,4厘米;
④8厘米,8厘米,2厘米;
答:能围成4种不同的等腰三角形。
故选:B。
【名师点评】此题主要依据三角形的周长的意义,以及三角形的三条边的关系,解决问题。
2.【考点】长方形的周长.
【答案】D
【思路分析】根据长方形的周长公式:C=(a+b)×2,那么a+b=C÷2,据此求出长与宽的和,进而确定有几种不同的围法。
【解答】解:12÷2=6
6=5+1=4+2=3+3
可以围成长是5、宽是1的长方形,长是4、宽是2的长方形,边长是3的正方形。
答:有3种不同围法。
故选:D。
【名师点评】此题考查的目的是理解掌握长方形、正方形周长的意义及应用。
3.【考点】排列组合.
【答案】B
【思路分析】因为加上两边两个站,一共有4个站,先求出线段条数,一条线段就是一种票价.再考虑往返情况,乘以2就可以.
【解答】解:此题相当于一条线段上有4个点,
有多少种不同的票价即有多少条线段:3+2+1=6(种);
有多少种车票是要考虑顺序的,则有6×2=12(种).
答:一共要准备12种不同的车票.
故选:B.
【名师点评】此题要注意来回的车票种类是不同的,所以要乘上2.
4.【考点】最大与最小.
【答案】A
【思路分析】利用直线两两相交图形,数一数交点的个数即是最少需要舞蹈演员人数,据此解答即可。
【解答】解:如图:,
当5条直线两两相交时,需要的舞蹈演员最少,此时5条直线有10个交点,每一条直线上有4个交点,正好是每排4名演员的位置,所以最少需要舞蹈演员10名。
故选:A。
【名师点评】本题主要考查了最少问题,解题的关键是理解直线两两相交时需要的舞蹈演员最少,利用图形更易理解。
5.【考点】排列组合.
【答案】B
【思路分析】如果含有5元的有:5+5、5+2+2+1,2种;
如果含有2元的有:2+2+2+2+2、2+2+2+2+1+1,2种;
根据加法原理,可得共有:2+2=4(种);据此解答.
【解答】解:含有5元的有:5+5、5+2+2+1,2种;
含有2元的有:2+2+2+2+2、2+2+2+2+1+1,2种;
共有:2+2=4(种);
答:小红一共有4种不同的付钱方法.
故选:B.
【名师点评】本题考查了加法原理即完成一件事情有n类方法,第一类中又有M1种方法,第二类中又有M2种方法,…,第n类中又有 Mn种方法,那么完成这件事情就有M1+M2+…+Mn种方法.
6.【考点】长方形、正方形的面积.
【答案】D
【思路分析】要使围成长方形的面积最大,也就是长和宽的差最小(接近正方形),首先铁丝的长度除以2求出长与宽,进而确定长和宽,然后根据长方形的面积=长×宽,把数据代入公式解答.
【解答】解:18÷2=9(厘米),
则长为5厘米、宽为4厘米时面积最大,
5×4=20(平方厘米),
答:围成长方形的面积最大是20平方厘米.
故选:D.
【名师点评】此题主要考查长方形的周长搜狗、面积公式的灵活运用,关键是熟记公式,明确:长和宽的差最小(接近正方形)面积最大,
7.【考点】筛选与枚举.
【答案】C
【思路分析】分选择1个、2个或者3个砝码,找出其能组合成的所有的质量即可.
【解答】解:(1)每个砝码单独称量时,可以称量出10克、20克、50克三种重量;
(2)三个砝码两两组合称量时,可以称量出:
10+20=30克,
10+50=60克,
20+50=70克,
三种重量;
(3)三个砝码一起称量时,可以称量出:
10+20+50=80克,
3+3+1=7(种),
答:用这三个砝码可以在天平上直接称出7种不同重量的物体.
故选:C.
【名师点评】正确的进行分类,列举出所有的可能即可求解.
8.【考点】数字问题.
【答案】B
【思路分析】设这个数为(a≠0,b≠0),根据题意可得:10b+a﹣10a﹣b=18,整理得b=a+2,然后讨论a、b的取值范围即可得出答案。
【解答】解:设这个数为(a≠0,b≠0),根据题意可得:
10b+a﹣10a﹣b=18
整理得:b=a+2
所以,2<a+2≤9
所以,0<a≤7
所以,a可以是1、2、3、4、5、6、7;对应着b可以是3、4、5、6、7、8、9,
所以,这样的数有7个。
故选:B。
【名师点评】本题考查了数的位置原则,关键是得到十位上的数和个位上的数的等量关系。
9.【考点】百数表.
【答案】A
【思路分析】观察百数表可得:从左边第一列开始,个数数字分别依次是1、2、3、4、5、6、7、8、9、0,据此可得盖住的三个数字从上到下依次是14、23、32,据此把这三个数字加起来即可解答问题.
【解答】解:根据题干分析可得:14+23+32=69
答:这三个数字之和可能是69.
故选:A。
【名师点评】解答此题关键是明确百数表的中数字的排列规律,从而得出盖住的三个数字分别是几,再相加即可.
10.【考点】排列组合.
【答案】C
【思路分析】如果先确定第一名,有3种选择;那么第二名就有2种选择;第三名就有1种选择;然后根据乘法原理,就可求出获得前三名的可能不同的情况,即3×2×1=6种,然后解答即可。
【解答】解:因为没有并列名次,所以可得:
3×2×1=6(种)
答:他们三人获得前三名的情况共有6种。
故选:C。
【名师点评】本题考查了乘法原理,即做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。
二.填空题(共14小题)
11.【考点】逻辑推理.
【答案】2。
【思路分析】甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘,则每位同学都要与其他四位同学各赛一盘,即每人都要赛4盘,已知此时甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;由于丁此时只赛了1盘,则丁这一盘是与甲赛的,与其他人还没有下;乙赛了三 盘,则乙这三盘是与甲、丙、小强赛的;丙赛了2盘,则这两盘是与甲、乙赛的;所以此时小强与甲、乙赛了2盘;据此推理即可。
【解答】解:由于此时甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;
丁此时只赛了1盘,则丁这一盘是与甲赛的,与其他人还没有赛;
乙赛了三 盘,则乙这三盘是与甲、丙、小强赛的;
丙赛了2盘,则这两盘是与甲、乙赛的;
所以此时小强赛了2盘,是与甲、乙赛的。
答:小强已经赛了2盘。
故答案为:2。
【名师点评】根据每人需要赛的总盘数及此时每人已赛的盘数进行分析推理是完成此类问题的关键。
12.【考点】筛选与枚举.
【答案】见试题解答内容
【思路分析】(1)先选原先单个的砝码,有3种不同的质量,再两个搭配,得出不同的质量,最后三个搭配得出不同的质量;
(2)类比(1)的方法,一一列举解决问题.
【解答】解:(1)一个砝码:2克,3克,4克共3种不同的质量,
两个砝码搭配:2克+3克=5克,2克+4克=6克,3克+4克=7克,共3种不同的质量,
三个搭配:2克+3克+4克=9克,
共有:3+3+1=7(种);
(2)一个砝码:2克,3克,4克,6克共4种不同的质量,
两个砝码搭配:2克+3克=5克,2克+4克=6克,3克+4克=7克,2克+6克=8克,3克+6克=9克,4克+6克=10克,共6种不同的质量,
三个搭配:2克+3克+4克=9克,2克+3克+6克=11克,6克+3克+4克=13克,2克+4克+6克=12克,
四个搭配:2克+3克+4克+6克=15克有1种不同的质量,
去掉2种重复的质量;
共有:4+6+4+1﹣2=13(种);
故答案为:7;13.
【名师点评】利用列举法注意分类的标准,一一列举做到不重不漏.
13.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】当取出1张人民币时,可以组成3种不同的钱数;当取出2张人民币时可以组成3种不同的钱数,由此得出答案.
【解答】解:当取出1张人民币时,可以组成1元、2元、5元,3种不同的钱数;
取出2张人民币时可以组成:1+2=3元、1+5=6元、2+5=7元,3种不同的钱数;
一共可以组成3+3=6种不同的钱数.
故答案为:6.
【名师点评】关键分两种情况分别找出组成的不同的钱数,注意要做到不重复、不遗漏.
14.【考点】筛选与枚举.
【答案】见试题解答内容
【思路分析】4个砝码中选1个有4种:1克、2克、4克、8克;4个砝码中选2个,有6种:3克、5克、9克、6克、10克、12克;4个砝码中选3个,有4种:7克、11克、14克、13克;4个砝码都选出只有一种:15克;四种情况的方法加起来,即可得解.
【解答】解:选1个有4种:1克、2克、4克、8克,
选2个,有6种:3克、5克、9克、6克、10克、12克,
选3个,有4种:7克、11克、14克、13克,
选4个,只有一种:15克;
4+6+4+1=15(种),
答:最多可以称出15种不同重量的物体.
故答案为:15.
【名师点评】此题考查了组合问题,分类解决此类组合问题,用加法原理.
15.【考点】握手问题.
【答案】见试题解答内容
【思路分析】每两个队之间赛一场,那么每个队要赛5场,一共是6×5=30(场),但是甲队与乙队比赛和乙队与甲队比赛是同一场比赛,所以30场比赛就多算了一倍,再除以2即可.
【解答】解:6×(6﹣1)÷2
=6×5÷2
=30÷2
=15(场)
答:一共要举行15场比赛.
故答案为:15.
【名师点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解.
16.【考点】握手问题.
【答案】见试题解答内容
【思路分析】本题属于握手问题,3个小朋友每两人通一次电话,则每个小朋友都要和其他2个人通一次电话,即每个人要打2次电话,共有3个小朋友,所以共打3×2=6次,打电话是在两个人之间进行的,所以他们互通电话共6÷2=3次.
【解答】解:3×2÷2=3(次)
答:一共可以通话3次.
故答案为:3.
【名师点评】本题属于握手问题,根据握手总次数的计算方法来求解,握手次数总和的计算方法:握手次数=人数×(人数﹣1)÷2,握手次数的公式要记住,并灵活运用.
17.【考点】握手问题.
【答案】见试题解答内容
【思路分析】有6名学生参加聚会,每两人握一次手,即每人都要和其他5人握一次手,每人需握5次,共有6人,共握手5×6=30次,握手是在两人之间进行的,去掉重复计算的情况,实际只有30÷2=15次.
【解答】解:6×(6﹣1)÷2
=6×5÷2
=15(次)
答:一共握了15次手.
故答案为:15.
【名师点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人比较多可以用公式:握手次数=人数×(人数﹣1)÷2解答.
18.【考点】排列组合.
【答案】见试题解答内容
【思路分析】根据加法原理,利用“标数法”画图解答即可,注意只许向东或向南行,否则会有重复的情况.
【解答】解:标数法如下:
答:一共有6种不同的路线.
故答案为:6.
【名师点评】解答最短的路线问题,利用“标数法”画图解答是最直观不易出错的最佳方法,特别是复杂的图形;注意一定不要走“回头路”.
19.【考点】简单周期现象中的规律.
【答案】15。
【思路分析】每4天一循环,第四次去少年宫就是第3组循环零2天。据此解答。
【解答】解:3×4+2
=12+2
=14(天)
7月1日+14天=7月15日
答:小敏第4次去少年宫是7月15日。
故答案为:15。
【名师点评】先找到规律,再根据规律求解。
20.【考点】日期和时间的推算.
【答案】7时15分,17。
【思路分析】根据题干,早晨6:00发第一辆,到第六辆车发车,之间有6﹣1=5个间隔时间,即经过了15×5=75分钟,据此用开始发车的时间+经过的时间即可求出第六辆车的发车时间;
用上午10:00减去第一辆车发出的时间,求出经过的时间,再除以15,求出间隔数,加上1即可解答问题。
【解答】解:15×5=75(分钟)
75分钟=1小时15分
6时+1时15分=7时15分
10时﹣6时=4时
4时=240分
240÷15+1
=16+1
=17(辆)
答:第六辆车的发车时间是7时15分,上午10:00发第17辆车。
故答案为:7时15分,17。
【名师点评】考查了日期和时间的推算,本题的难点是求出中间的时间,发车间隔的次数。同时注意单位的换算。
21.【考点】逻辑推理.
【答案】见试题解答内容
【思路分析】由题意,在图上分别标明小明、小红、小强和小胜,根据小明已经赛了3场,小红赛了2场,小胜赛了1场,在图上连线表示出他们比赛的对阵情况,即可得解.
【解答】解:
由图可知,小强赛了2场.
答:小强赛了2场.
故答案为:2.
【名师点评】解答此题要注意小胜赛了1场,是与小明赛的,所以小红赛的两场是与小明和小强.
22.【考点】逻辑推理.
【答案】见试题解答内容
【思路分析】五人进行比赛,每两人都要比赛一盘,则每个人都要每其他4人进行一场比赛,即每人要赛4场:
小林已赛4盘,即小林已和小王、小李、小张、小许各赛一盘;
小王已赛3盘,因为小张只赛过一盘,这一盘是和小林下的.所以小王这三盘是和小林、小李、小许下的;
此时小张二盘已满.
则小许和小林与小王各赛一盘,即已赛了2盘.
【解答】解:由题意可知,每人要进行5﹣1=4场比赛:
小林已赛4盘,小王已赛3盘,小李已赛2盘,小张已赛1盘,
则小林已赛4盘,即小林已和小王、小李、小张、小许各赛一盘;
小张只赛过一盘,这一盘是和小林下的.
所以小王三盘是和小林、小李、小许下的;
此时小张二盘已满.
则小许和小林与小王各赛一盘,即已赛了2盘.
故答案为:2.
【名师点评】根据每人需赛的盘数及已赛的盘数之间的逻辑关系,进行分析排除是完成本题的关键.
23.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】用7、9、4三个数字组成不同的三位数,三个数字填三个空,分步完成,第一步,先填百位数字,有3种可能;第二步,十位数字从剩下的2个中选一个,有2种选法;第三步,剩下的1个数字填在各位,只有1种选法;分步解决用乘法.
【解答】解:3×2×1=6(个);
答:用7、9、4三个数字可以组成6个不同的三位数.
故答案为:6.
【名师点评】此题考查了简单的排列组合,做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2不同的方法,…,做第n步有mn不同的方法.那么完成这件事共有 N=m1m2m3…mn 种不同的方法.
24.【考点】简单的排列、组合.
【答案】见试题解答内容
【思路分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加.
【解答】解:①订阅1种时:可以是任意1种,有3种方法;
②订阅2种时,是从三种中任选2种,共有3种方法;
③订阅3种时就是3份报纸都订阅,有1种方法;
共有:3+3+1=7(种);
答:一共有7种订阅方法.
故答案为:7.
【名师点评】本题分情况讨论后,每一种情况都可以看成简单的组合问题.
三.判断题(共8小题)
25.【考点】三角形边的关系.
【答案】√
【思路分析】根据三角形三条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答即可。
【解答】解:因为2+3=5(厘米)
5厘米大于4厘米
所以用2厘米、3厘米、4厘米三根小棒可以围成一个三角形;
因为3+4=7(厘米)
7厘米大于6厘米
所以用3厘米、4厘米、6厘米三根小棒可以围成一个三角形;
因此,从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。
故答案为:√。
【名师点评】此题考查的目的是理解掌握三角形三条边之间的关系及应用。
26.【考点】图形的拼组.
【答案】√
【思路分析】因18的因数有1,2,3,6,9,18,用18个小正方形拼成的长方形,根据拼成图形的长和宽,求出它们的周长,再进行比较。据此解答。
【解答】解:用18个1平方厘米的小正方形拼成长方形,拼成后长方形的长和宽可分下列情况:
a、长18厘米,宽1厘米,
b、长9厘米,宽2厘米,
c、长6厘米,宽3厘米,
答:一共有3种不同的拼法。原题说法正确。
故答案为:√。
【名师点评】解答本题关键是分情况讨论组成长方形的长和宽。
27.【考点】排列组合;握手问题.
【答案】×
【思路分析】每两个队之间都要赛一场,那么每个队要赛5场,一共是6×5=30(场),但是甲队与乙队比赛和乙队与甲队比赛是同一场比赛,所以30场比赛就多算了一倍,再除以2即可。
【解答】解:6×(6﹣1)÷2
=6×5÷2
=30÷2
=15(场)
即一共要赛15场,所以原题说法错误。
故答案为:×。
【名师点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
28.【考点】日期和时间的推算.
【答案】×
【思路分析】根据经过时间=结束时刻﹣开始时刻,求出上午9时到上午11时经过了多久,再求出里面有几个40分钟,最后加上开始的一次,即可求出上午11时是第几场。
【解答】解:11时﹣9时=2时=120分钟
120÷40+1
=3+1
=4(场)
答:第4场次正好开始放映。
故答案为:×。
【名师点评】解答此题的关键是掌握经过时间=结束时刻﹣开始时刻这个公式。
29.【考点】排列组合.
【答案】×
【思路分析】因为每个人都要与其他3人比赛,所以共要比赛12场,因为比赛是两个人之间进行的,所以重复算了一次,再除以2即可。
【解答】解:4×(4﹣1)÷2
=12÷2
=6(场)
即一共要比赛6场,所以原题说法错误。
故答案为:×。
【名师点评】此类赛制为单循环赛制,比赛场数=参赛人数×(人数﹣1)÷2。
30.【考点】植树问题.
【答案】见试题解答内容
【思路分析】一根木料锯成3段,锯了:3﹣1=2次,共用了3.6分钟,那么锯一次用:3.6÷2=1.8(分);锯成5段,锯了:5﹣1=4次,要用:1.8×4=7.2(分钟);据此解答.
【解答】解:3.6÷(3﹣1)×(5﹣1)
=1.8×4
=7.2(分钟)
即:把它锯成5段要用7.2分钟;所以原题说法错误.
故答案为:×.
【名师点评】本题考查了植树问题,知识点是:锯木次数=段数﹣1.
31.【考点】整数、小数复合应用题.
【答案】×
【思路分析】丽丽借给芳芳2.5元后,丽丽的钱减少了2.5元,而芳芳的钱增加了2.5元,后来他们两人的钱数一样多,说明丽丽比芳芳多2个2.5元,由此求解。
【解答】解:丽丽减少2.5元,芳芳增加2.5元,这时他们的钱数相等,所以原来两人的差是:
2.5×2=5(元)
原题说法是错误的。
故答案为:×。
【名师点评】解决本题关键是知道丽丽减少和芳芳增加是同时的,所以两人相差了2个2.5元,而不是2.5元。
32.【考点】简单的排列、组合;排列组合;筛选与枚举.
【答案】×
【思路分析】将8个相同的小球分成4堆,可以利用列举法解答。
【解答】解:(1,1,1,5)、(1,1,2,4)、(1,1,3,3)、(1、2、2、3)、(2、2、2、2),共有5种不同的分法;所以原题说法错误。
故答案为:×。
【名师点评】解答本题要注意按顺序列举,防止遗漏。
四.应用题(共7小题)
33.【考点】简单的排列、组合;排列组合.
【答案】6种。
【思路分析】第一个吃的有3种选择,第二个吃的有2种选择,第三个吃的有1种选择,然后根据乘法原理解答即可。
【解答】解:3×2×1=6(种)
答:可以有6种不同顺序的吃法。
【名师点评】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
34.【考点】简单的排列、组合;最大与最小;排列组合.
【答案】24;6858。
【思路分析】(1)先排百位有4种选择,再排十位有3种选择,然后排个位有2种选择,最后排一位数有1种选择,然后根据乘法原理解答即可。
(2)根据数位知识及乘法算式的性质可知,乘法算式中的因数越大,积就越大;根据数位知识可知,一个数的高位上数字越大,其值就越大;由此可知,用2、6、7、9这四个数字组成三位数乘一位数的算式,三位数是762,一位数是9;据此解答即可。
【解答】解:(1)4×3×2×1=24(个)
(2)其中积最大是:762×9=6858
答:有24个不同的算式,其中积最大是6858。
【名师点评】本题考查了乘法原理和极值问题,注意:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
35.【考点】逻辑推理.
【答案】两场。
【思路分析】由于共五位同学参赛,进行循环赛,即每个人都要与其它四人赛一场.由题意可知,A赛了4场,则B、C、D、E都与A赛了一场;B赛了3场,则是与A、C、E各赛了一场(由于D只赛了一场已与A赛过);C赛了两场即是与A、B赛的,所以E赛了两场,即是与A、B赛的。
【解答】解:由赛制可知:A赛了4场,则B、C、D、E都与A赛了一场;
B赛了3场,则是与A、C、E各赛了一场(由于D只赛了一场已与A赛过);
C赛了两场即是与A、B赛的,
所以此时E赛了两场,即是与A、B赛的。
答:此时E赛了两场。
【名师点评】根据循环赛的规则与每人比赛的场数之间的逻辑关系推出每人分别与谁进行了比赛是完成本题的关键。
36.【考点】简单的排列、组合;排列组合.
【答案】7种。
【思路分析】根据题意可得:借阅一本有3种方法,借阅两本有3种方法,借阅三本有1种方法,然后根据加法原理解答即可。
【解答】解:3+3+1=7(种)
答:共有7种借阅方法。
【名师点评】用两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析要完成的“一件事”是什么,可以“分类”还是需要“分步”。
37.【考点】逻辑推理.
【答案】2场。
【思路分析】一共有6名同学,每两人都要赛一场,所以每人最多赛5场,根据小张和小王已经赛了5场,可得小张和小王与其余的人都比赛过了,小高赛了4场,去掉和小张、小王的两场比赛,应该和小于、小赵的比赛,小于和小赵赛了3场,这3场就是小张、小王和小高的比赛,六个人只有小李和小张、小王赛过,就是2场比赛,据此解答。
【解答】解:根据分析可知,小张、小王和其余的人都赛过了,小高赛了4场,说明小高和小张、小王、小于、小赵都赛过了;没有和小李赛过;小于和小赵赛了3场,说明小于、小赵与小张、小王、小高赛过了;也没有和小李赛过,小李只和小张、小王赛过;小李只赛过2场。
答:小李只赛了2场。
【名师点评】本题考查逻辑思维推理问题的应用,关键是判断出小张、小王、小高与哪位赛过了。
38.【考点】简单的排列、组合;排列组合.
【答案】(1)3种;(2)9种。
【思路分析】(1)小红买两种点心,即3选2,然后根据握手问题公式“n(n﹣1)÷2”即可求出一共有几种不同的选法。
(2)从3种豆浆中选一种有3种选法,从3种点心中选一种有3种选法,然后根据乘法原理解答即可。
【解答】解:(1)3×(3﹣1)÷2
=6÷2
=3(种)
答:一共有3种不同的选法。
(2)3×3=9(种)
答:小亮要买一种豆浆和一种点心,有9种不同的选法。
【名师点评】(1)本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式 n(n﹣1)÷2解答。
39.【考点】日期和时间的推算;周期性问题.
【答案】9:02,9:42。
【思路分析】由题意得:8时38分﹣8时30分=8分钟,8时46分﹣8时38分=8分钟,8时54分﹣8时46分=8分钟,即每8分钟到站一辆2路公共汽车,由此分别在之后每到站的时刻加上8分钟,然后再进行比较,据此推算即可。
【解答】解:8时38分﹣8时30分=8分钟
8时46分﹣8时38分=8分钟
8时54分﹣8时46分=8分钟
由此可知:每8分钟到站一辆2路公共汽车。
则:8时54分+8分钟=9时2分
9时2分+8分钟=9时10分
9时10分+8分钟=9时18分
9时18分+8分钟=9时26分
9时26分+8分钟=9时34分
9时34分+8分钟=9时42分
9时42分+8分钟=9时50分
9时50分+8分钟=9时58分
9时58分+8分钟=10时6分
10时6分+8分钟=10时14分
10时14分+8分钟=10时22分
10时22分+8分钟=10时30分
10时30分+8分钟=10时38分
10时38分+8分钟=10时46分
10时46分+8分钟=10时54分
10时54分+8分钟=11时2分
由此可得:2路车到站的时刻为9:02,9:42。
答:2路车到站的时刻为9:02,9:42。
【名师点评】此题考查周期性问题。关键在于找到每8分钟到站一辆2路公共汽车。
21世纪教育网(www.21cnjy.com)
