常见函数应用模型重点考点 专题练 2026年高考数学一轮复习备考
文档属性
| 名称 | 常见函数应用模型重点考点 专题练 2026年高考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 11:40:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
常见函数应用模型重点考点 专题练
2026年高考数学一轮复习备考
一、单选题
1.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,经验表明,某种绿茶用的开水泡制,再等茶水温度降至时饮用,可以产生最佳口感,如果茶水原来的温度是,经过一定时间后的温度T(单位:)可由公式求得,其中表示室温,k是一个随着物体与空气的接触状况而定的正常数.现有一杯的绿茶放在室温为的房间中,如果茶温降到需要 ,那么在室温下,用的开水泡制,刚泡好的茶水要达到最佳饮用口感,大约需要放置( )(参考数据:)
A. B. C. D.
2.某池塘里原有一块浮萍,浮萍蔓延后的面积S(单位:平方米)与时间t(单位:月)的关系式为(,且),图象如图所示.则下列结论正确的个数为( )
①浮萍每个月增长的面积都相等;
②浮萍蔓延4个月后,面积超过30平方米;
③浮萍面积每个月的增长率均为50%;
④若浮萍蔓延到3平方米、4平方米、12平方米所经过的时间分别是,,,则.
A.0 B.1 C.2 D.3
3.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系.(a,b.为常数),若该果蔬在7℃的保鲜时间为288小时,在21℃ 的保鲜时间为32小时,且该果蔬所需物流时间为4天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过( )
A.14℃ B.15℃ C.13℃ D.16℃
4.沙漏也叫做沙钟,是一种测量时间的装置.现有一个沙漏(如图)上方装有的细沙,细沙从中间小孔由上方慢慢漏下,经过分钟时剩余的细沙量为,且(为常数),经过分钟时,上方还剩下一半细沙,要使上方细沙是开始时的,需经过的时间为( )
A.分钟 B.分钟 C.分钟 D.分钟
5.薯条作为一种油炸食品,风味是决定其接受程度的基础.米其林三星餐厅大厨Heston Blumenthal对餐饮门店的不同油炸批次的薯条进行整体品质的感官评价并提出了“油炸质量曲线”(图1),将油炸过程划分为五个阶段:诱导、新鲜、最佳、降解和废弃阶段,以解释食物品质与油炸时间之间的关系.
在特定条件下,薯条品质得分与煎炸时间(单位:min)满足函数关系(a、b、c是常数),图2记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳煎炸时间为( )
A.2.25min B.2.75min C.3.25min D.3.75min
6.遗忘曲线是由德国心理学家艾宾浩斯研究发现的,它描述了人类大脑对新事物遗忘的规律.某同学根据自己记忆100个英语新单词的经历,用画图软件拟合了自己的遗忘曲线,得到其记忆率(记住的单词个数占总单词数的百分比)与初次记忆经过的时间(单位:小时)的函数关系式为,当记住的单词仅剩25个时,则离初次记忆经过了( )(参考数据:)
A.100小时 B.300小时 C.1000小时 D.3000小时
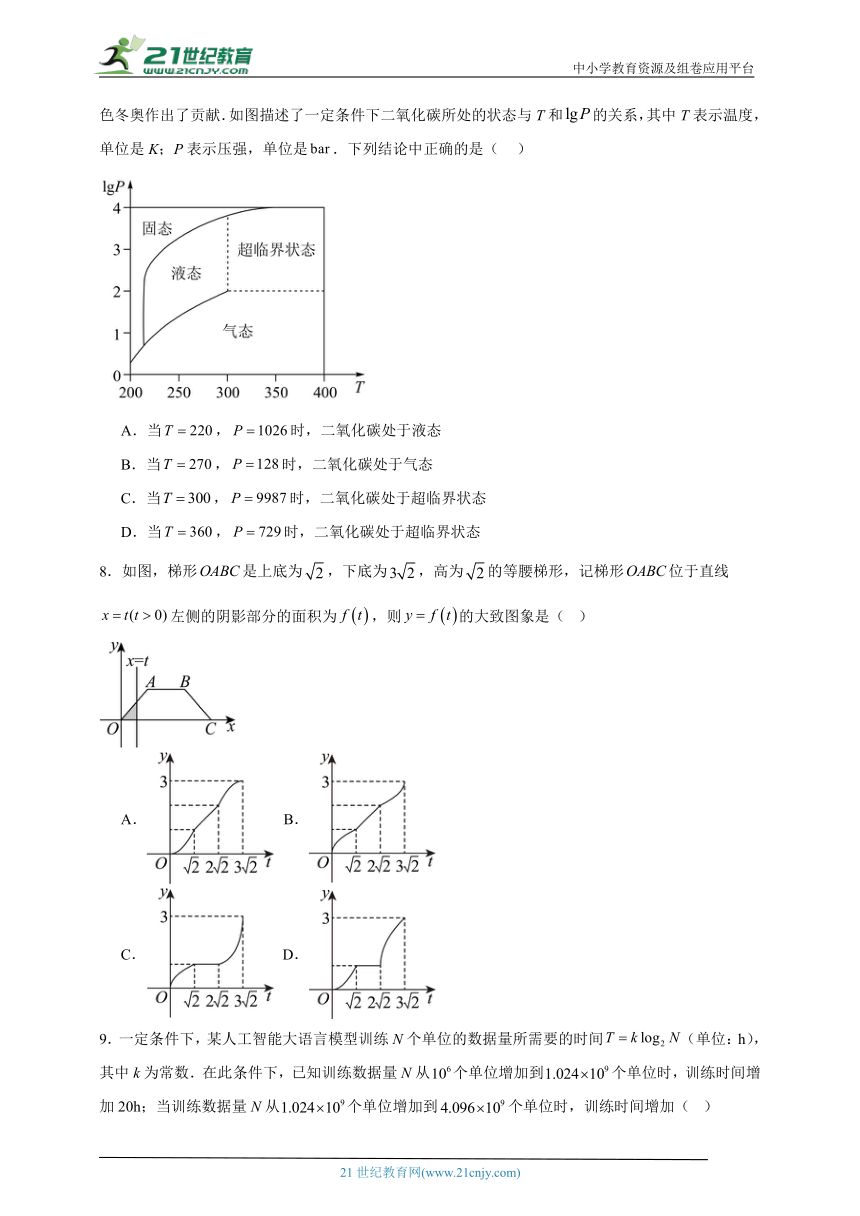
7.在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和的关系,其中T表示温度,单位是K;P表示压强,单位是.下列结论中正确的是( )
A.当,时,二氧化碳处于液态
B.当,时,二氧化碳处于气态
C.当,时,二氧化碳处于超临界状态
D.当,时,二氧化碳处于超临界状态
8.如图,梯形是上底为,下底为,高为的等腰梯形,记梯形位于直线左侧的阴影部分的面积为,则的大致图象是( )
A. B.
C. D.
9.一定条件下,某人工智能大语言模型训练N个单位的数据量所需要的时间(单位:h),其中k为常数.在此条件下,已知训练数据量N从个单位增加到个单位时,训练时间增加20h;当训练数据量N从个单位增加到个单位时,训练时间增加( )
A.2h B.4h C.20h D.40h
10.2024年1月17日我国自行研制的天舟七号货运飞船在发射3小时后成功对接于空间站天和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物体追踪技术,设计了如下实验:目标P在地面轨道上做匀速直线运动;在地面上相距的A,B两点各放置一个传感器,分别实时记录A,B两点与物体P的距离.科技小组的同学根据传感器的数据,绘制了“距离-时间”函数图像,分别如曲线a,b所示.和分别是两个函数的极小值点.曲线a经过和,曲线b经过.已知,并且从时刻到时刻P的运动轨迹与线段AB相交.分析曲线数据可知,P的运动轨迹与直线AB所成夹角的正弦值以及P的速度大小分别为( )
A. B.
C. D.
二、多选题
11.把物体放在冷空气中冷却,如果物体原来的温度是,空气的温度是,那么后物体的温度(单位:)可由公式求得,其中是一个随着物体与空气的接触状况而定的正常数.已知.( )
A.若,则经过后,该物体的温度降为原来的
B.若,则存在,使得经过后物体的温度是经过后物体温度的2倍
C.若,且,则
D.若,且是的导数,则
12.小菲在学校选修课中了解到艾宾浩斯遗忘曲线,为了解自己记忆一组单词的情况,她记录了随后一个月的有关数据,绘制图象,拟合了记忆保持量与时间(天)之间的函数关系,则下列说法正确的是( )
A.随着时间的增加,小菲的单词记忆保持量降低
B.第一天小菲的单词记忆保持量下降最多
C.9天后,小菲的单词记忆保持量低于
D.26天后,小菲的单词记忆保持量不足
13.环境监测设备在污染物浓度实时监测中起到关键作用.研究发现,设备对污染物的动态响应关系可用“环境监测函数”近似描述,其监测值,,其中x表示污染物浓度,a为设备灵敏度参数越大,灵敏度越高,则( )
A.过定点
B.在污染物浓度区间上单调递增
C.关于对称
D.取定x的值,灵敏度越高,监测值越大
14.当一束光通过一个吸光物质(通常为溶液)时,溶质吸收了光能,光的强度减弱;吸光度就是用来衡量光被吸收程度的一个物理量,其影响因素有溶剂、浓度、温度.分析物浓度越高,穿过材料的光子被吸收的机会就越大.吸光度的测量简便高效,因此被广泛应用于液体和气体的光谱测量技术,集成至工业测试系统,还可以用于科研分析.其中透光率是指光子通过物体的能量占发出光能量的比例.在实际生产和生活中,通常用吸光度A和透光率T来衡量物体材料的透光性能,著名的朗伯—比尔定律表明了两者之间的等量关系为,其中,是吸光度,为透光率,为入射光强度,为透射光强度,某化学有机高分子材料研究所测得了如下表不同有机高分子材料的透光率:
有机高分子材料 塑料 纤维 薄膜
0.6 0.7 0.8
设塑料、纤维、薄膜的吸光度分别为,,,则( )
A. B. C. D.
三、填空题
15.研究发现:汽车在高速公路上行驶,发现紧急情况需要刹车时,刹车距离反应距离+制动距离.其中反应距离与汽车行驶速度成正比,比例系数为;制动距离与汽车行驶速度的平方成正比,比例系数为.下表是通过试验观测得到的、、的对应关系:
56 11.9 0.213 16.0 0.00510
64 13.4 0.209 21.9 0.00535
72 15.2 0.211 28.2 0.00544
80 16.7 0.209 36.0 0.00563
89 18.6 0.209 45.3 0.00572
97 20.1 0.207 55.5 0.00590
105 21.9 0.209 67.2 0.00610
用表中比例系数与的平均数作为参数、的估计值.那么根据上表数据,估计时,刹车距离约为 .(结果精确到0.1)
16.根据统计数据可将某池塘里浮萍的面积单位:与时间单位:月的关系近似表示为如图所示函数关系,已知第1个月时,浮萍面积为,第5个月时,浮萍面积就会超过,下列函数模型:①,②,③,④中,最符合浮萍面积y与时间t关系的模型是 填写序号,若浮萍蔓延到,所经过的时间 .
17.道路通行能力指单位时间(1小时)内通过道路上指定断面的最大车辆数,是度量道路疏导交通能力的指标.同时为了行驶安全,车辆之间必须保持一定的安全距离.为了研究某城市道路通行能力,现给出如下假设:
假设1:车身长度均为4.8米;
假设2:所有车辆以相同的速度(单位:千米/小时)匀速行驶;
假设3:安全距离(单位:米)与车辆速度近似满足.
该城市道路通行能力的最大值约为 .(结果保留整数)
18.李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付 元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为 .
四、解答题
19.某城市为了鼓励居民节约用电采用阶梯电价的收费方式,即每户用电量不超过的部分按0.6元收费,超过的部分,按1.2元收费.设某用户的用电量为,对应电费为元.
(1)请写出关于的函数解析式;
(2)某居民本月的用电量为,求此用户本月应缴纳的电费.
20.将连续正整数1,2,,从小到大排列构成一个数,为这个数的位数(如时,此数为123456789101112,共15个数字,,现从这个数中随机取一个数字,为恰好取到0的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字0的个数,为这个数中数字9的个数,,,,,求当时的最大值.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C C D A B B
题号 11 12 13 14
答案 AC ABC AB ABC
1.C
【分析】一杯的绿茶放在室温为的房间中,茶温降到需要 代入公式得;茶温降到需要代入公式得,结合题中数据可求得.
【详解】因为一杯的绿茶放在室温为的房间中,如果茶温降到需要 ,
则,整理得,解得,
一杯的绿茶放在室温为的房间中,如果茶温降到需要,
则,整理得,解得,
所以大约需要.
故选:C.
2.B
【分析】由已知可得出,计算出萍蔓延1月至2月份增长的面积和2月至3月份增长的面积,可判断①的正误;计算出浮萍蔓延4个月后的面积,可判断②的正误;计算出浮萍蔓延每个月增长率,可判断③的正误;利用指数运算可判断④的正误.
【详解】由已知可得,则.
对于①,浮萍蔓延1月至2月份增长的面积为(平方米),
浮萍蔓延2月至3月份增长的面积为(平方米),①错;
对于②,浮萍蔓延4个月后的面积为(平方米),②对;
对于③,浮萍蔓延第至个月的增长率为,所以,浮萍蔓延每个月增长率相同,都是,③错;
对于④,若浮萍蔓延到3平方米、4平方米、12平方米所经过的时间分别是,,,
则,,,所以,④错.
故选:B.
3.A
【分析】根据给定的函数模型建立方程组,再列出不等式即可求解.
【详解】依题意,,则,即,显然,
设物流过程中果蔬的储藏温度为t℃,于是,
解得,因此,
所以物流过程中果蔬的储藏温度最高不能超过14℃.
故选:A
4.C
【分析】根据分钟时,上方还剩下一半细沙,可列出方程,求出的值,然后令为原来的,即可求出结果.
【详解】依题意有,即,
两边取对数得,所以,得到,
当容器上方细沙只有开始时的时,则有,所以,
两边取对数得,所以,
即需要经过的时间为分钟.
故选:C
5.C
【分析】将三点坐标代入解析式求出参数,然后根据二次函数对称性可得.
【详解】由图2知,解得,,,
所以,
所以当时,取得最大值.
故选:C.
6.C
【分析】利用对数性质求解指数方程可得答案.
【详解】由题意得,所以,即,
两边同时取以10为底的对数,得,所以.
故选:C.
7.D
【分析】根据与的关系图可得正确的选项.
【详解】当,时,,此时二氧化碳处于固态,故A错误.
当,时,,此时二氧化碳处于液态,故B错误.
当,时,与4非常接近,故此时二氧化碳处于固态,对应的是非超临界状态,故C错误.
当,时,因, 故此时二氧化碳处于超临界状态,故D正确.
故选:D
8.A
【分析】写出的表达式,再根据分段函数性质选出图象即可.
【详解】根据题意可知在梯形中,;
当时,阴影部分为等腰直角三角形,其面积为;
当时,阴影部分为等腰直角三角形加上一个矩形,
其面积为;
当时,阴影部分面积为整个梯形面积减去右侧空白部分表面积,
即;
所以可得;
根据函数类型对比图象可得A正确.
故选:A
9.B
【分析】由题给条件列出不同训练数据量时所需的时间,结合对数的运算性质即可求解.
【详解】设当N取个单位、个单位、个单位时所需时间分别为,
由题意,,
,
,
因为,所以,
所以,
所以当训练数据量N从个单位增加到个单位时,训练时间增加4小时.
故选:B.
10.B
【分析】建系,设点,作相应的辅助线,分析可知,结合分析求解即可.
【详解】如图,建立平面直角坐标系,
设动点P的轨迹与y轴重合,其在时刻对应的点分别为(坐标原点),,P的速度为,
因为,可得,
由题意可知:均与y轴垂直,且,
作垂足为,则,
因为,即,解得;
又因为∥y轴,可知P的运动轨迹与直线AB所成夹角即为,
所以P的运动轨迹与直线AB所成夹角的正弦值为.
故选:B.
【点睛】关键点点睛:建系,设动点P的轨迹与y轴重合,以坐标系为依托,把对应的量转化为相应的长度,进而分析求解.
11.AC
【分析】结合题意,代入公式,逐项判断,即可得到本题答案.
【详解】把,代入,得,解得,则,故A正确;
根据题意,,化简得,,因为,所以方程无解,故B错误;
因为,,所以,
所以,即,故C正确;
因为,所以,
所以
,即,故D错误.
故选:AC
12.ABC
【分析】结合函数性质与图象逐项分析即可得.
【详解】由函数及在定义域内都为减函数,
且,故随着的增加而减少,故A正确;
结合图象及指数函数的性质可得第一天小菲的单词记忆保持量下降最多,故B正确;
当时,,则,
即9天后,小菲的单词记忆保持量低于,故C正确;
,故D错误.
故选:ABC.
13.AB
【分析】对于A,令,可求得定点,即可判断A;对于B,对求导,判断导函数在时的正负,即可判断B;对于C,由B即可判断;对于D,以a为自变量构造新函数,求导,判断单调性即可.
【详解】解:对于A,在中,令,则,所以过定点,故A正确;
对于B,因为
则注意到当,,
则在上单调递增,故B正确;
对于C,由B选项知为单调递增函数,故不存在对称轴,故C错误;
对于D,以a为自变量,设为,
则
,因为,故,
所以的正负取决于,当时
,即当时,随着a的增大,减小,故D错误
故选:
14.ABC
【分析】根据题意计算出,结合对数式的运算法则和对数函数的单调性,即可依次判断各选项.
【详解】由题意可知:,,,
对于A,,而在定义域内单调递增,且,
所以,即,所以,又,
所以,故A正确;
对于B,,
因为,所以,即,所以,故B正确;
对于C,,
因为,所以,即,所以,故C正确;
对于D,,,
,
,
,
所以,则有,
又,则,故D错误.
故选:ABC
15.
【分析】设刹车距离为,求出、的平均值,可得出的表达式,代值计算可得的值.
【详解】设刹车距离为,由题意可得,
由表格中的数据可得,
,
所以,,故.
所以,当时,刹车距离约为.
故答案为:.
16. ③
【分析】由已知结合基本初等函数的图象判断函数模型,求出函数解析式,即可求解
【详解】为线性增长,的增长速度会逐渐变慢,
由图象可知,模型①④不符合,
将,代入模型②③,得,,即模型②,模型③,
当时,模型②,不符合,
当时,模型③,,选模型③;
由,解得
故答案为:③;
17.821
【分析】由题意,先进行单位换算统一单位,整理函数解析式,利用基本不等式,可得答案.,
【详解】1小时秒,车辆速度(千米/小时)换算为米/秒是米/秒.
1小时内通过的车辆数
.
根据基本不等式(),,
当且仅当时等号成立.所以,
即该城市道路通行能力的最大值约为821.
故答案为:821.
18. 130. 15.
【分析】由题意可得顾客需要支付的费用,然后分类讨论,将原问题转化为不等式恒成立的问题可得的最大值.
【详解】(1),顾客一次购买草莓和西瓜各一盒,需要支付元.
(2)设顾客一次购买水果的促销前总价为元,
元时,李明得到的金额为,符合要求.
元时,有恒成立,即,即元.
所以的最大值为.
【点睛】本题主要考查不等式的概念与性质 数学的应用意识 数学式子变形与运算求解能力,以实际生活为背景,创设问题情境,考查学生身边的数学,考查学生的数学建模素养.
19.(1)
(2)156元
【分析】(1)根据题意分和两种情况讨论即可;
(2)结合(1)将代入函数解析式即可.
【详解】(1)由题意得,当时,,
当时,,
综上所述,;
(2)当用电为时,由(1)知,
所以元,
所以此用户本月应交156元.
20.(1)(2)(3)
【分析】(1)根据题意,首先分析时,这个数的位数,进而可得其中0的个数,有等可能事件的概率公式,计算可得答案;
(2)分,,,,四种情况讨论这个数的组成情况,综合即可得;
(3)根据题意,分情况求出当时的表达式,比较其最大值的大小,即可得答案.
【详解】(1)当时,,即这个数中共有192个数字,
其中数字0的个数为11,
则恰好取到0的概率为;
(2)当时,这个数有1位数组成,,
当时,这个数有9个1位数组成,个两位数组成,则,
当时,这个数有9个1位数组成,90个两位数组成,个三位数组成,,
当时,这个数有9个1位数组成,90个两位数组成,900个三位数组成,个四位数组成,,
;
(3)当时,,
当,,,时,
当时,,
即,同理有,
由,可知、19、29、39、49、59、69、79、89、90,
所以当时,,19、29,39,49,59,69,79,89,;
当时,(9),
当时,,
当时,,
由关于单调递增,故当时,的最大值为,
又,所以当时,的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
常见函数应用模型重点考点 专题练
2026年高考数学一轮复习备考
一、单选题
1.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,经验表明,某种绿茶用的开水泡制,再等茶水温度降至时饮用,可以产生最佳口感,如果茶水原来的温度是,经过一定时间后的温度T(单位:)可由公式求得,其中表示室温,k是一个随着物体与空气的接触状况而定的正常数.现有一杯的绿茶放在室温为的房间中,如果茶温降到需要 ,那么在室温下,用的开水泡制,刚泡好的茶水要达到最佳饮用口感,大约需要放置( )(参考数据:)
A. B. C. D.
2.某池塘里原有一块浮萍,浮萍蔓延后的面积S(单位:平方米)与时间t(单位:月)的关系式为(,且),图象如图所示.则下列结论正确的个数为( )
①浮萍每个月增长的面积都相等;
②浮萍蔓延4个月后,面积超过30平方米;
③浮萍面积每个月的增长率均为50%;
④若浮萍蔓延到3平方米、4平方米、12平方米所经过的时间分别是,,,则.
A.0 B.1 C.2 D.3
3.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系.(a,b.为常数),若该果蔬在7℃的保鲜时间为288小时,在21℃ 的保鲜时间为32小时,且该果蔬所需物流时间为4天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过( )
A.14℃ B.15℃ C.13℃ D.16℃
4.沙漏也叫做沙钟,是一种测量时间的装置.现有一个沙漏(如图)上方装有的细沙,细沙从中间小孔由上方慢慢漏下,经过分钟时剩余的细沙量为,且(为常数),经过分钟时,上方还剩下一半细沙,要使上方细沙是开始时的,需经过的时间为( )
A.分钟 B.分钟 C.分钟 D.分钟
5.薯条作为一种油炸食品,风味是决定其接受程度的基础.米其林三星餐厅大厨Heston Blumenthal对餐饮门店的不同油炸批次的薯条进行整体品质的感官评价并提出了“油炸质量曲线”(图1),将油炸过程划分为五个阶段:诱导、新鲜、最佳、降解和废弃阶段,以解释食物品质与油炸时间之间的关系.
在特定条件下,薯条品质得分与煎炸时间(单位:min)满足函数关系(a、b、c是常数),图2记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳煎炸时间为( )
A.2.25min B.2.75min C.3.25min D.3.75min
6.遗忘曲线是由德国心理学家艾宾浩斯研究发现的,它描述了人类大脑对新事物遗忘的规律.某同学根据自己记忆100个英语新单词的经历,用画图软件拟合了自己的遗忘曲线,得到其记忆率(记住的单词个数占总单词数的百分比)与初次记忆经过的时间(单位:小时)的函数关系式为,当记住的单词仅剩25个时,则离初次记忆经过了( )(参考数据:)
A.100小时 B.300小时 C.1000小时 D.3000小时
7.在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和的关系,其中T表示温度,单位是K;P表示压强,单位是.下列结论中正确的是( )
A.当,时,二氧化碳处于液态
B.当,时,二氧化碳处于气态
C.当,时,二氧化碳处于超临界状态
D.当,时,二氧化碳处于超临界状态
8.如图,梯形是上底为,下底为,高为的等腰梯形,记梯形位于直线左侧的阴影部分的面积为,则的大致图象是( )
A. B.
C. D.
9.一定条件下,某人工智能大语言模型训练N个单位的数据量所需要的时间(单位:h),其中k为常数.在此条件下,已知训练数据量N从个单位增加到个单位时,训练时间增加20h;当训练数据量N从个单位增加到个单位时,训练时间增加( )
A.2h B.4h C.20h D.40h
10.2024年1月17日我国自行研制的天舟七号货运飞船在发射3小时后成功对接于空间站天和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物体追踪技术,设计了如下实验:目标P在地面轨道上做匀速直线运动;在地面上相距的A,B两点各放置一个传感器,分别实时记录A,B两点与物体P的距离.科技小组的同学根据传感器的数据,绘制了“距离-时间”函数图像,分别如曲线a,b所示.和分别是两个函数的极小值点.曲线a经过和,曲线b经过.已知,并且从时刻到时刻P的运动轨迹与线段AB相交.分析曲线数据可知,P的运动轨迹与直线AB所成夹角的正弦值以及P的速度大小分别为( )
A. B.
C. D.
二、多选题
11.把物体放在冷空气中冷却,如果物体原来的温度是,空气的温度是,那么后物体的温度(单位:)可由公式求得,其中是一个随着物体与空气的接触状况而定的正常数.已知.( )
A.若,则经过后,该物体的温度降为原来的
B.若,则存在,使得经过后物体的温度是经过后物体温度的2倍
C.若,且,则
D.若,且是的导数,则
12.小菲在学校选修课中了解到艾宾浩斯遗忘曲线,为了解自己记忆一组单词的情况,她记录了随后一个月的有关数据,绘制图象,拟合了记忆保持量与时间(天)之间的函数关系,则下列说法正确的是( )
A.随着时间的增加,小菲的单词记忆保持量降低
B.第一天小菲的单词记忆保持量下降最多
C.9天后,小菲的单词记忆保持量低于
D.26天后,小菲的单词记忆保持量不足
13.环境监测设备在污染物浓度实时监测中起到关键作用.研究发现,设备对污染物的动态响应关系可用“环境监测函数”近似描述,其监测值,,其中x表示污染物浓度,a为设备灵敏度参数越大,灵敏度越高,则( )
A.过定点
B.在污染物浓度区间上单调递增
C.关于对称
D.取定x的值,灵敏度越高,监测值越大
14.当一束光通过一个吸光物质(通常为溶液)时,溶质吸收了光能,光的强度减弱;吸光度就是用来衡量光被吸收程度的一个物理量,其影响因素有溶剂、浓度、温度.分析物浓度越高,穿过材料的光子被吸收的机会就越大.吸光度的测量简便高效,因此被广泛应用于液体和气体的光谱测量技术,集成至工业测试系统,还可以用于科研分析.其中透光率是指光子通过物体的能量占发出光能量的比例.在实际生产和生活中,通常用吸光度A和透光率T来衡量物体材料的透光性能,著名的朗伯—比尔定律表明了两者之间的等量关系为,其中,是吸光度,为透光率,为入射光强度,为透射光强度,某化学有机高分子材料研究所测得了如下表不同有机高分子材料的透光率:
有机高分子材料 塑料 纤维 薄膜
0.6 0.7 0.8
设塑料、纤维、薄膜的吸光度分别为,,,则( )
A. B. C. D.
三、填空题
15.研究发现:汽车在高速公路上行驶,发现紧急情况需要刹车时,刹车距离反应距离+制动距离.其中反应距离与汽车行驶速度成正比,比例系数为;制动距离与汽车行驶速度的平方成正比,比例系数为.下表是通过试验观测得到的、、的对应关系:
56 11.9 0.213 16.0 0.00510
64 13.4 0.209 21.9 0.00535
72 15.2 0.211 28.2 0.00544
80 16.7 0.209 36.0 0.00563
89 18.6 0.209 45.3 0.00572
97 20.1 0.207 55.5 0.00590
105 21.9 0.209 67.2 0.00610
用表中比例系数与的平均数作为参数、的估计值.那么根据上表数据,估计时,刹车距离约为 .(结果精确到0.1)
16.根据统计数据可将某池塘里浮萍的面积单位:与时间单位:月的关系近似表示为如图所示函数关系,已知第1个月时,浮萍面积为,第5个月时,浮萍面积就会超过,下列函数模型:①,②,③,④中,最符合浮萍面积y与时间t关系的模型是 填写序号,若浮萍蔓延到,所经过的时间 .
17.道路通行能力指单位时间(1小时)内通过道路上指定断面的最大车辆数,是度量道路疏导交通能力的指标.同时为了行驶安全,车辆之间必须保持一定的安全距离.为了研究某城市道路通行能力,现给出如下假设:
假设1:车身长度均为4.8米;
假设2:所有车辆以相同的速度(单位:千米/小时)匀速行驶;
假设3:安全距离(单位:米)与车辆速度近似满足.
该城市道路通行能力的最大值约为 .(结果保留整数)
18.李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付 元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为 .
四、解答题
19.某城市为了鼓励居民节约用电采用阶梯电价的收费方式,即每户用电量不超过的部分按0.6元收费,超过的部分,按1.2元收费.设某用户的用电量为,对应电费为元.
(1)请写出关于的函数解析式;
(2)某居民本月的用电量为,求此用户本月应缴纳的电费.
20.将连续正整数1,2,,从小到大排列构成一个数,为这个数的位数(如时,此数为123456789101112,共15个数字,,现从这个数中随机取一个数字,为恰好取到0的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字0的个数,为这个数中数字9的个数,,,,,求当时的最大值.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C C D A B B
题号 11 12 13 14
答案 AC ABC AB ABC
1.C
【分析】一杯的绿茶放在室温为的房间中,茶温降到需要 代入公式得;茶温降到需要代入公式得,结合题中数据可求得.
【详解】因为一杯的绿茶放在室温为的房间中,如果茶温降到需要 ,
则,整理得,解得,
一杯的绿茶放在室温为的房间中,如果茶温降到需要,
则,整理得,解得,
所以大约需要.
故选:C.
2.B
【分析】由已知可得出,计算出萍蔓延1月至2月份增长的面积和2月至3月份增长的面积,可判断①的正误;计算出浮萍蔓延4个月后的面积,可判断②的正误;计算出浮萍蔓延每个月增长率,可判断③的正误;利用指数运算可判断④的正误.
【详解】由已知可得,则.
对于①,浮萍蔓延1月至2月份增长的面积为(平方米),
浮萍蔓延2月至3月份增长的面积为(平方米),①错;
对于②,浮萍蔓延4个月后的面积为(平方米),②对;
对于③,浮萍蔓延第至个月的增长率为,所以,浮萍蔓延每个月增长率相同,都是,③错;
对于④,若浮萍蔓延到3平方米、4平方米、12平方米所经过的时间分别是,,,
则,,,所以,④错.
故选:B.
3.A
【分析】根据给定的函数模型建立方程组,再列出不等式即可求解.
【详解】依题意,,则,即,显然,
设物流过程中果蔬的储藏温度为t℃,于是,
解得,因此,
所以物流过程中果蔬的储藏温度最高不能超过14℃.
故选:A
4.C
【分析】根据分钟时,上方还剩下一半细沙,可列出方程,求出的值,然后令为原来的,即可求出结果.
【详解】依题意有,即,
两边取对数得,所以,得到,
当容器上方细沙只有开始时的时,则有,所以,
两边取对数得,所以,
即需要经过的时间为分钟.
故选:C
5.C
【分析】将三点坐标代入解析式求出参数,然后根据二次函数对称性可得.
【详解】由图2知,解得,,,
所以,
所以当时,取得最大值.
故选:C.
6.C
【分析】利用对数性质求解指数方程可得答案.
【详解】由题意得,所以,即,
两边同时取以10为底的对数,得,所以.
故选:C.
7.D
【分析】根据与的关系图可得正确的选项.
【详解】当,时,,此时二氧化碳处于固态,故A错误.
当,时,,此时二氧化碳处于液态,故B错误.
当,时,与4非常接近,故此时二氧化碳处于固态,对应的是非超临界状态,故C错误.
当,时,因, 故此时二氧化碳处于超临界状态,故D正确.
故选:D
8.A
【分析】写出的表达式,再根据分段函数性质选出图象即可.
【详解】根据题意可知在梯形中,;
当时,阴影部分为等腰直角三角形,其面积为;
当时,阴影部分为等腰直角三角形加上一个矩形,
其面积为;
当时,阴影部分面积为整个梯形面积减去右侧空白部分表面积,
即;
所以可得;
根据函数类型对比图象可得A正确.
故选:A
9.B
【分析】由题给条件列出不同训练数据量时所需的时间,结合对数的运算性质即可求解.
【详解】设当N取个单位、个单位、个单位时所需时间分别为,
由题意,,
,
,
因为,所以,
所以,
所以当训练数据量N从个单位增加到个单位时,训练时间增加4小时.
故选:B.
10.B
【分析】建系,设点,作相应的辅助线,分析可知,结合分析求解即可.
【详解】如图,建立平面直角坐标系,
设动点P的轨迹与y轴重合,其在时刻对应的点分别为(坐标原点),,P的速度为,
因为,可得,
由题意可知:均与y轴垂直,且,
作垂足为,则,
因为,即,解得;
又因为∥y轴,可知P的运动轨迹与直线AB所成夹角即为,
所以P的运动轨迹与直线AB所成夹角的正弦值为.
故选:B.
【点睛】关键点点睛:建系,设动点P的轨迹与y轴重合,以坐标系为依托,把对应的量转化为相应的长度,进而分析求解.
11.AC
【分析】结合题意,代入公式,逐项判断,即可得到本题答案.
【详解】把,代入,得,解得,则,故A正确;
根据题意,,化简得,,因为,所以方程无解,故B错误;
因为,,所以,
所以,即,故C正确;
因为,所以,
所以
,即,故D错误.
故选:AC
12.ABC
【分析】结合函数性质与图象逐项分析即可得.
【详解】由函数及在定义域内都为减函数,
且,故随着的增加而减少,故A正确;
结合图象及指数函数的性质可得第一天小菲的单词记忆保持量下降最多,故B正确;
当时,,则,
即9天后,小菲的单词记忆保持量低于,故C正确;
,故D错误.
故选:ABC.
13.AB
【分析】对于A,令,可求得定点,即可判断A;对于B,对求导,判断导函数在时的正负,即可判断B;对于C,由B即可判断;对于D,以a为自变量构造新函数,求导,判断单调性即可.
【详解】解:对于A,在中,令,则,所以过定点,故A正确;
对于B,因为
则注意到当,,
则在上单调递增,故B正确;
对于C,由B选项知为单调递增函数,故不存在对称轴,故C错误;
对于D,以a为自变量,设为,
则
,因为,故,
所以的正负取决于,当时
,即当时,随着a的增大,减小,故D错误
故选:
14.ABC
【分析】根据题意计算出,结合对数式的运算法则和对数函数的单调性,即可依次判断各选项.
【详解】由题意可知:,,,
对于A,,而在定义域内单调递增,且,
所以,即,所以,又,
所以,故A正确;
对于B,,
因为,所以,即,所以,故B正确;
对于C,,
因为,所以,即,所以,故C正确;
对于D,,,
,
,
,
所以,则有,
又,则,故D错误.
故选:ABC
15.
【分析】设刹车距离为,求出、的平均值,可得出的表达式,代值计算可得的值.
【详解】设刹车距离为,由题意可得,
由表格中的数据可得,
,
所以,,故.
所以,当时,刹车距离约为.
故答案为:.
16. ③
【分析】由已知结合基本初等函数的图象判断函数模型,求出函数解析式,即可求解
【详解】为线性增长,的增长速度会逐渐变慢,
由图象可知,模型①④不符合,
将,代入模型②③,得,,即模型②,模型③,
当时,模型②,不符合,
当时,模型③,,选模型③;
由,解得
故答案为:③;
17.821
【分析】由题意,先进行单位换算统一单位,整理函数解析式,利用基本不等式,可得答案.,
【详解】1小时秒,车辆速度(千米/小时)换算为米/秒是米/秒.
1小时内通过的车辆数
.
根据基本不等式(),,
当且仅当时等号成立.所以,
即该城市道路通行能力的最大值约为821.
故答案为:821.
18. 130. 15.
【分析】由题意可得顾客需要支付的费用,然后分类讨论,将原问题转化为不等式恒成立的问题可得的最大值.
【详解】(1),顾客一次购买草莓和西瓜各一盒,需要支付元.
(2)设顾客一次购买水果的促销前总价为元,
元时,李明得到的金额为,符合要求.
元时,有恒成立,即,即元.
所以的最大值为.
【点睛】本题主要考查不等式的概念与性质 数学的应用意识 数学式子变形与运算求解能力,以实际生活为背景,创设问题情境,考查学生身边的数学,考查学生的数学建模素养.
19.(1)
(2)156元
【分析】(1)根据题意分和两种情况讨论即可;
(2)结合(1)将代入函数解析式即可.
【详解】(1)由题意得,当时,,
当时,,
综上所述,;
(2)当用电为时,由(1)知,
所以元,
所以此用户本月应交156元.
20.(1)(2)(3)
【分析】(1)根据题意,首先分析时,这个数的位数,进而可得其中0的个数,有等可能事件的概率公式,计算可得答案;
(2)分,,,,四种情况讨论这个数的组成情况,综合即可得;
(3)根据题意,分情况求出当时的表达式,比较其最大值的大小,即可得答案.
【详解】(1)当时,,即这个数中共有192个数字,
其中数字0的个数为11,
则恰好取到0的概率为;
(2)当时,这个数有1位数组成,,
当时,这个数有9个1位数组成,个两位数组成,则,
当时,这个数有9个1位数组成,90个两位数组成,个三位数组成,,
当时,这个数有9个1位数组成,90个两位数组成,900个三位数组成,个四位数组成,,
;
(3)当时,,
当,,,时,
当时,,
即,同理有,
由,可知、19、29、39、49、59、69、79、89、90,
所以当时,,19、29,39,49,59,69,79,89,;
当时,(9),
当时,,
当时,,
由关于单调递增,故当时,的最大值为,
又,所以当时,的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
