第三章实数单元测试卷(含答案)浙教版2025—2026学年七年级上册
文档属性
| 名称 | 第三章实数单元测试卷(含答案)浙教版2025—2026学年七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 21:31:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章实数单元测试卷浙教版2025—2026学年七年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.下列各数中,是无理数的是( )
A. B. C. D.3.1415926
2.的相反数是( )
A. B. C.2 D.4
3.下列说法错误的是( )
A.相反数等于本身的数只有0 B.平方后等于本身的数只有0,1
C.立方后等于本身的数是0, D.绝对值等于本身的数只有0,1
4.下列各式中错误的是( )
A. B. C. D.
5.已知,则的值为( )
A.2 B.4 C.6 D.无法确定
6.已知是5的算术平方根,则的立方根是( )
A. B. C. D.2
7.已知(其中、为最接近的正整数),则的值为( )
A.13 B.14 C.15 D.16
8.已知一个正数的两个平方根分别是和,则的值是( )
A. B.5 C. D.25
9.如图所示,数轴上表示3、的对应点分别为C、B,点C是的中点,则点A表示的数是( )
A.- B.6- C.-3 D.+3
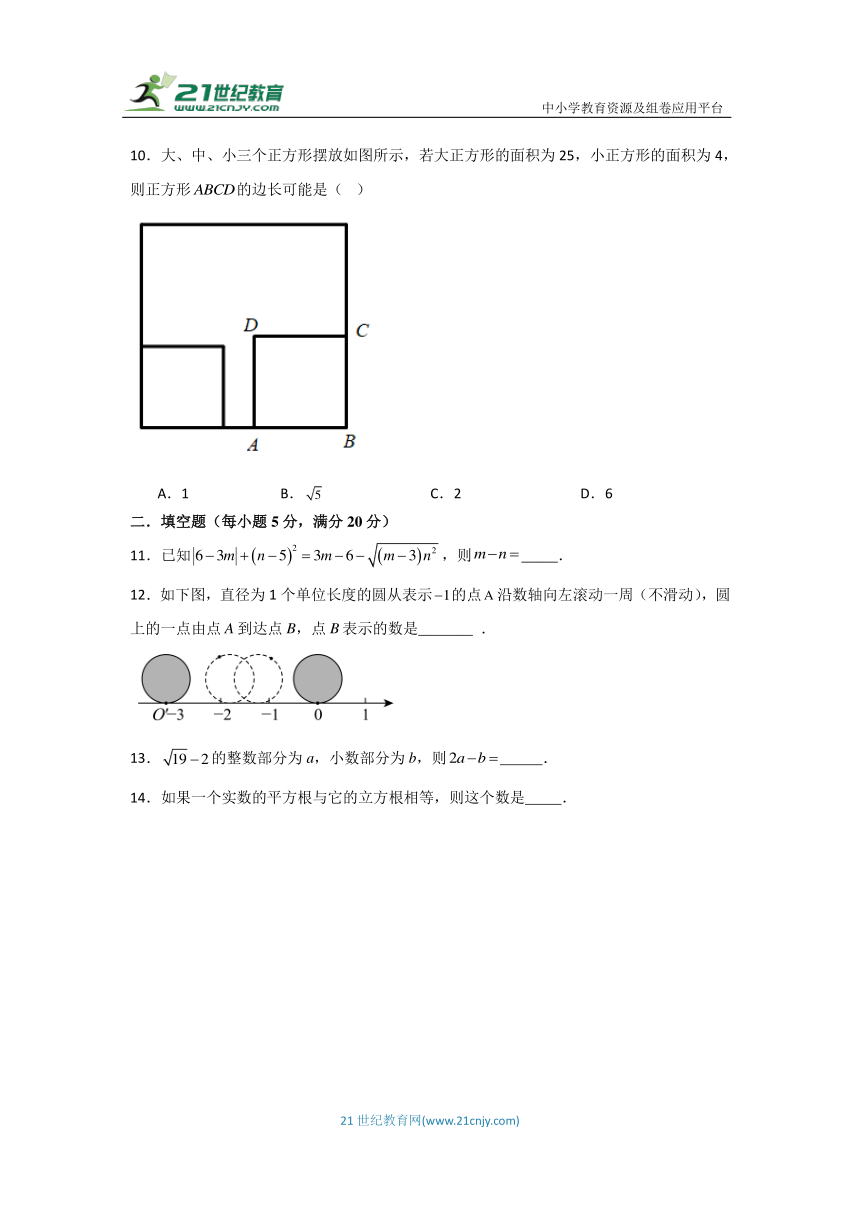
10.大、中、小三个正方形摆放如图所示,若大正方形的面积为25,小正方形的面积为4,则正方形的边长可能是( )
A.1 B. C.2 D.6
二.填空题(每小题5分,满分20分)
11.已知,则 .
12.如下图,直径为1个单位长度的圆从表示的点沿数轴向左滚动一周(不滑动),圆上的一点由点A到达点B,点B表示的数是 .
13.的整数部分为a,小数部分为b,则 .
14.如果一个实数的平方根与它的立方根相等,则这个数是 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.计算:.
16.已知和是a的两个不同的平方根,是a的立方根.
(1)求x,y,a的值.
(2)求的立方根.
17.已知的平方根为,的立方根为.
(1)求,的值;
(2)求的算术平方根.
18.(1)________________________________;(用“>”“<”或“=”填空)
(2)由(1)可知:
①________;
②________;
③________;(结果保留根号)
(3)计算:.(结果保留根号)
19.在学习《实数》时,我们思考了在网格中画格点(网格线的交点)正方形(顶点都在格点上的正方形)的问题.如图,这是由边长为1的小正方形组成的网格.
(1)网格中以为边的格点正方形的面积是________.如图,以原点O为圆心,长为半径画弧,与数轴正半轴交于点B,则点B表示的数m为________,说明可以在数轴上表示________(填“有理数”或“无理数”).
(2)仿照(1)中的思路,在网格中设计以为边的正方形,并求出线段的长.
(3)若C,D两点分别表示实数c和d,且有与互为相反数.求的立方根.
20.观察下表,并解决问题.
a 0.0004 0.04 4 400 40000
0.02 0.2 2 20 200
(1)根据上表,可以得到被开方数和它的算术平方根之间的小数点的变化规律:若被开方数的小数点向右(或向左)移动两位,则它的算术平方根的小数点就相应地向右(或向左)移动______位.
(2)已知,,则______.
(3)根据上述探究过程类比研究一个数的立方根,已知,,,则______.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D D C C C D B B
二、填空题
11.【解】解:当时,变为,
∴,
∴或,
解得,
∵
∴
∴不符合题意,舍去,
当时,
∵,且,
∴,
∴,
∵,
∴,
即,
∴,,
解得,,
∴.
综上,.
故答案为:.
12.【解】解:∵圆的周长为,
∴圆从表示的点A沿数轴向左滚动一周(不滑动),圆上的一点由点A到达点B,点B表示的数是:,
故答案为:.
13.【解】解:∵,
∴
∵的整数部分为a,小数部分为b,
∴,,
∴,
故答案为:.
14.【解】解:设这个实数为,
当时,它的平方根是0,立方根是0,二者相等,符合题意;
当时,它的平方根是,立方根是.若,两边同时六次方得,解得或(舍去),当时,它的一个平方根1与它的立方根1相等,符合题意;
当时,它没有实数平方根.
综上,这个数是0或1.
故答案为:0或1.
三、解答题
15.【解】解:原式
.
16.【解】(1)解:∵和是a的两个不同的平方根,
∴,
解得;
∴,
∴;
∵是a的立方根,
∴,
∴;
(2)由(1)知,,
∴,
∴的立方根是.
17.【解】(1)解:∵的平方根是,的立方根为,
∴,,
∴,.
(2)解:由(1)知,,
∴,
∵25的算术平方根为,
∴的算术平方根是5.
18.【解】解:(1)∵,
∴,
故答案为:<;<;<;<;
(2)∵,
∴,,,
∴①;
②;
③,
故答案为:①;②;③;
(3)
.
19.【解】(1)解:正方形的面积为,
,
由算术平方根得,
正方形的边长为,
是无理数;
故答案为:2;;无理数.
(2)解:如图,构造以为边的格点正方形(答案不唯一).
∵,
∴,
∴.
(3)解:由条件,可知,
∴,且,
解得,.
,
的立方根为2.
20.【解】(1)解:由表格数据可得:若被开方数的小数点向右(或向左)移动两位,则它的算术平方根的小数点就相应地向右(或向左)移动一位;
(2)解:∵,
∴;
(3)解:由题意并结合被开方数和它的算术平方根之间的小数点的变化规律可得:若被开立方数的小数点向右(或向左)移动三位,则它的立方根的小数点就相应地向右(或向左)移动一位;
∵,
∴.
21世纪教育网(www.21cnjy.com)
第三章实数单元测试卷浙教版2025—2026学年七年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.下列各数中,是无理数的是( )
A. B. C. D.3.1415926
2.的相反数是( )
A. B. C.2 D.4
3.下列说法错误的是( )
A.相反数等于本身的数只有0 B.平方后等于本身的数只有0,1
C.立方后等于本身的数是0, D.绝对值等于本身的数只有0,1
4.下列各式中错误的是( )
A. B. C. D.
5.已知,则的值为( )
A.2 B.4 C.6 D.无法确定
6.已知是5的算术平方根,则的立方根是( )
A. B. C. D.2
7.已知(其中、为最接近的正整数),则的值为( )
A.13 B.14 C.15 D.16
8.已知一个正数的两个平方根分别是和,则的值是( )
A. B.5 C. D.25
9.如图所示,数轴上表示3、的对应点分别为C、B,点C是的中点,则点A表示的数是( )
A.- B.6- C.-3 D.+3
10.大、中、小三个正方形摆放如图所示,若大正方形的面积为25,小正方形的面积为4,则正方形的边长可能是( )
A.1 B. C.2 D.6
二.填空题(每小题5分,满分20分)
11.已知,则 .
12.如下图,直径为1个单位长度的圆从表示的点沿数轴向左滚动一周(不滑动),圆上的一点由点A到达点B,点B表示的数是 .
13.的整数部分为a,小数部分为b,则 .
14.如果一个实数的平方根与它的立方根相等,则这个数是 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.计算:.
16.已知和是a的两个不同的平方根,是a的立方根.
(1)求x,y,a的值.
(2)求的立方根.
17.已知的平方根为,的立方根为.
(1)求,的值;
(2)求的算术平方根.
18.(1)________________________________;(用“>”“<”或“=”填空)
(2)由(1)可知:
①________;
②________;
③________;(结果保留根号)
(3)计算:.(结果保留根号)
19.在学习《实数》时,我们思考了在网格中画格点(网格线的交点)正方形(顶点都在格点上的正方形)的问题.如图,这是由边长为1的小正方形组成的网格.
(1)网格中以为边的格点正方形的面积是________.如图,以原点O为圆心,长为半径画弧,与数轴正半轴交于点B,则点B表示的数m为________,说明可以在数轴上表示________(填“有理数”或“无理数”).
(2)仿照(1)中的思路,在网格中设计以为边的正方形,并求出线段的长.
(3)若C,D两点分别表示实数c和d,且有与互为相反数.求的立方根.
20.观察下表,并解决问题.
a 0.0004 0.04 4 400 40000
0.02 0.2 2 20 200
(1)根据上表,可以得到被开方数和它的算术平方根之间的小数点的变化规律:若被开方数的小数点向右(或向左)移动两位,则它的算术平方根的小数点就相应地向右(或向左)移动______位.
(2)已知,,则______.
(3)根据上述探究过程类比研究一个数的立方根,已知,,,则______.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D D C C C D B B
二、填空题
11.【解】解:当时,变为,
∴,
∴或,
解得,
∵
∴
∴不符合题意,舍去,
当时,
∵,且,
∴,
∴,
∵,
∴,
即,
∴,,
解得,,
∴.
综上,.
故答案为:.
12.【解】解:∵圆的周长为,
∴圆从表示的点A沿数轴向左滚动一周(不滑动),圆上的一点由点A到达点B,点B表示的数是:,
故答案为:.
13.【解】解:∵,
∴
∵的整数部分为a,小数部分为b,
∴,,
∴,
故答案为:.
14.【解】解:设这个实数为,
当时,它的平方根是0,立方根是0,二者相等,符合题意;
当时,它的平方根是,立方根是.若,两边同时六次方得,解得或(舍去),当时,它的一个平方根1与它的立方根1相等,符合题意;
当时,它没有实数平方根.
综上,这个数是0或1.
故答案为:0或1.
三、解答题
15.【解】解:原式
.
16.【解】(1)解:∵和是a的两个不同的平方根,
∴,
解得;
∴,
∴;
∵是a的立方根,
∴,
∴;
(2)由(1)知,,
∴,
∴的立方根是.
17.【解】(1)解:∵的平方根是,的立方根为,
∴,,
∴,.
(2)解:由(1)知,,
∴,
∵25的算术平方根为,
∴的算术平方根是5.
18.【解】解:(1)∵,
∴,
故答案为:<;<;<;<;
(2)∵,
∴,,,
∴①;
②;
③,
故答案为:①;②;③;
(3)
.
19.【解】(1)解:正方形的面积为,
,
由算术平方根得,
正方形的边长为,
是无理数;
故答案为:2;;无理数.
(2)解:如图,构造以为边的格点正方形(答案不唯一).
∵,
∴,
∴.
(3)解:由条件,可知,
∴,且,
解得,.
,
的立方根为2.
20.【解】(1)解:由表格数据可得:若被开方数的小数点向右(或向左)移动两位,则它的算术平方根的小数点就相应地向右(或向左)移动一位;
(2)解:∵,
∴;
(3)解:由题意并结合被开方数和它的算术平方根之间的小数点的变化规律可得:若被开立方数的小数点向右(或向左)移动三位,则它的立方根的小数点就相应地向右(或向左)移动一位;
∵,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
