2026年高考数学一轮复习 统计(含解析)
文档属性
| 名称 | 2026年高考数学一轮复习 统计(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 553.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-10 19:37:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
高考数学一轮复习 统计
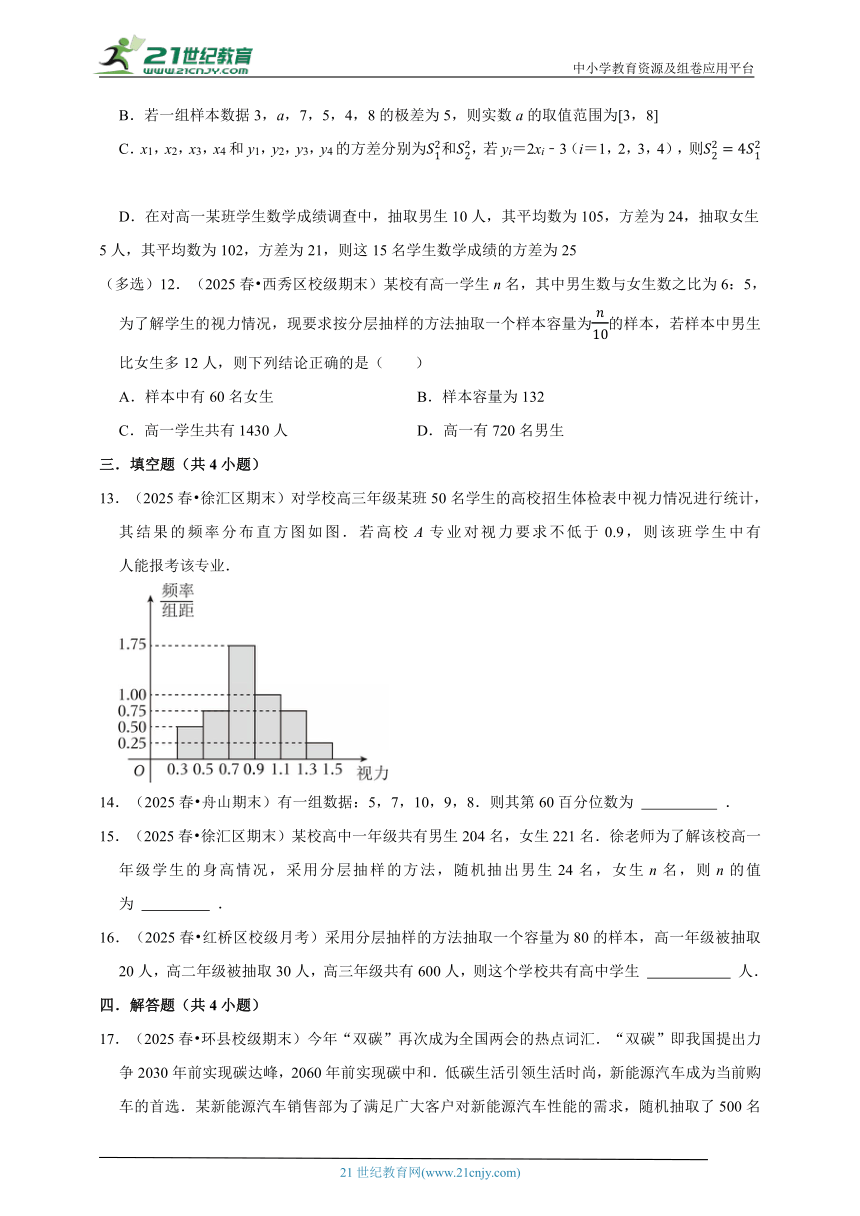
一.选择题(共8小题)
1.(2025春 商丘期末)已知两个变量x与y对应关系如下表:
x 1 2 3 4 5
y 5 7.5 n 9 10.5
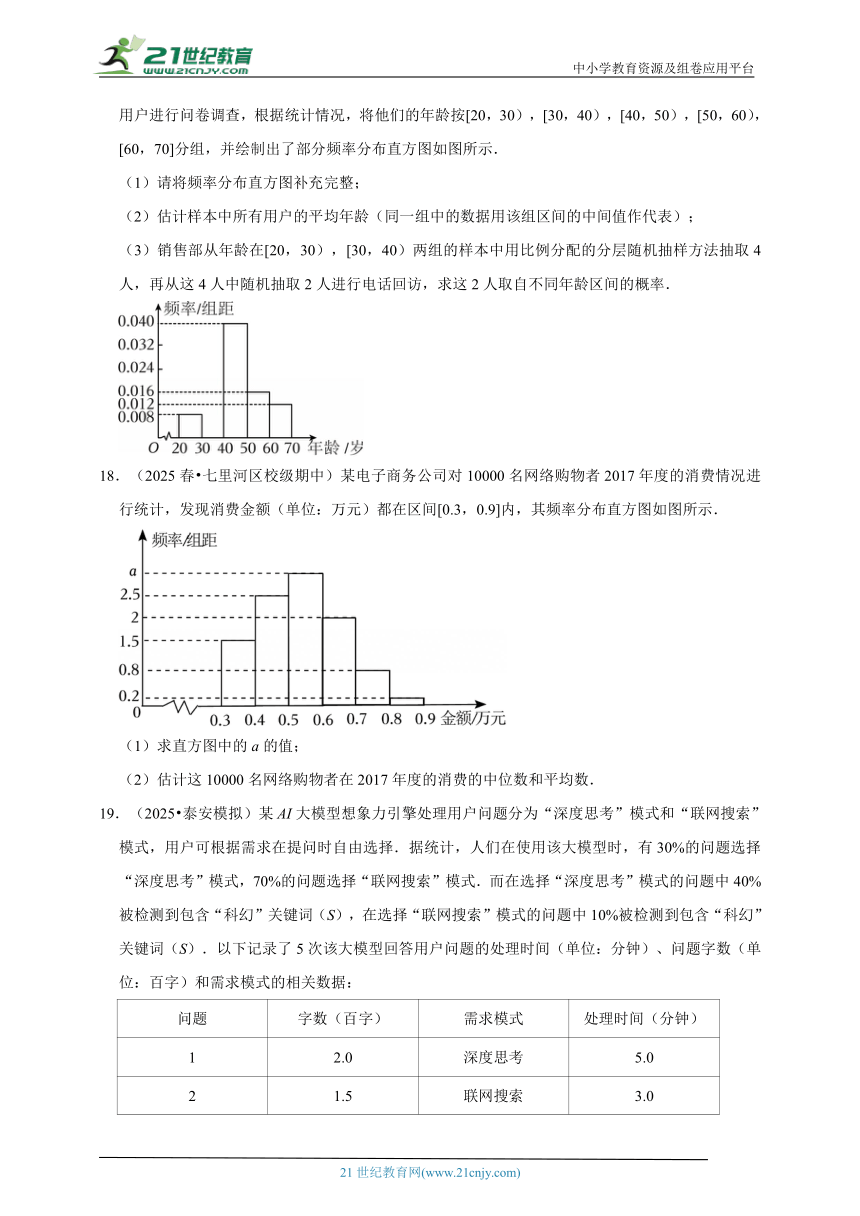
若y与x满足线性相关关系,且经验回归方程为,则下列说法正确的是( ).
A.y与x正相关
B.在x=4处的残差为0.25
C.n=8.5
D.变量x每增加一个单位,y的值一定增加1.25个单位
2.(2025春 郑州期末)数据5,7,3,2,11,13的第70百分位数为( )
A.7 B.11 C.13 D.17
3.(2025春 怀化期末)某同学8次考试的数学成绩从低到高分别为85,87,89,9θ,92,93,94,96,则这组成绩的75%分位数为( )
A.88 B.93 C.93.5 D.94
4.(2025 山东校级模拟)高二(1)班有40名学生,其中男生有16名,已知男生平均体重为68.4kg,总平均体重为60.1kg,则女生的平均体重约为( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
5.(2025 靖远县校级模拟)某社会实践基地,在实践结束后对学生进行考核评分,某班学生得分的条形图如图所示,则该班学生成绩的75%分位数为( )
A.79 B.83 C.87 D.88
6.(2025 安顺模拟)平均数、中位数和众数都是刻画一组数据的集中趋势的信息,它们的大小关系和数据分布的形态有关在如图分布形态中,a,b,c分别对应这组数据的平均数、中位数和众数,则下列关系正确的是( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
7.(2025春 青秀区校级月考)某学校有高中学生1000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380,为了调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,那么应抽取高二年级学生的人数为( )
A.50 B.60 C.70 D.80
8.(2025春 浦东新区校级期末)为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据如表可得回归直线方程x,其中0.78,,据此估计,该社区一户收入为16万元家庭年支出为( )
收入x万 8.3 8.6 9.9 11.1 12.1
支出y万 5.9 7.8 8.1 8.4 9.8
A.12.68万元 B.13.88万元 C.12.78万元 D.14.28万元
二.多选题(共4小题)
(多选)9.(2025春 温州期末)某电商平台决定对会员进行满意度调查.该平台共有2000名会员,其中女性会员1500人,男性会员500人,采用等比例分层随机抽样的方法抽取容量为80的样本.经计算得女性样本的满意度平均数为9,方差为2,男性样本的满意度平均数为8,方差为1,则( )
A.男性会员的样本容量为40
B.每位会员被抽到的概率为
C.估计该平台会员的满意度平均数为8.75
D.估计该平台会员满意度的方差为
(多选)10.(2025春 无锡期末)对于数据2,6,8,3,3,4,6,8,下列说法正确的是( )
A.极差为6 B.平均数为5 C.没有众数 D.中位数为5
(多选)11.(2025春 衢州期末)下列说法正确的是( )
A.数据2,3,4,5,6,7,8,9的第75百分位数为7
B.若一组样本数据3,a,7,5,4,8的极差为5,则实数a的取值范围为[3,8]
C.x1,x2,x3,x4和y1,y2,y3,y4的方差分别为和,若yi=2xi﹣3(i=1,2,3,4),则
D.在对高一某班学生数学成绩调查中,抽取男生10人,其平均数为105,方差为24,抽取女生5人,其平均数为102,方差为21,则这15名学生数学成绩的方差为25
(多选)12.(2025春 西秀区校级期末)某校有高一学生n名,其中男生数与女生数之比为6:5,为了解学生的视力情况,现要求按分层抽样的方法抽取一个样本容量为的样本,若样本中男生比女生多12人,则下列结论正确的是( )
A.样本中有60名女生 B.样本容量为132
C.高一学生共有1430人 D.高一有720名男生
三.填空题(共4小题)
13.(2025春 徐汇区期末)对学校高三年级某班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若高校A专业对视力要求不低于0.9,则该班学生中有 人能报考该专业.
14.(2025春 舟山期末)有一组数据:5,7,10,9,8.则其第60百分位数为 .
15.(2025春 徐汇区期末)某校高中一年级共有男生204名,女生221名.徐老师为了解该校高一年级学生的身高情况,采用分层抽样的方法,随机抽出男生24名,女生n名,则n的值为 .
16.(2025春 红桥区校级月考)采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,则这个学校共有高中学生 人.
四.解答题(共4小题)
17.(2025春 环县校级期末)今年“双碳”再次成为全国两会的热点词汇.“双碳”即我国提出力争2030年前实现碳达峰,2060年前实现碳中和.低碳生活引领生活时尚,新能源汽车成为当前购车的首选.某新能源汽车销售部为了满足广大客户对新能源汽车性能的需求,随机抽取了500名用户进行问卷调查,根据统计情况,将他们的年龄按[20,30),[30,40),[40,50),[50,60),[60,70]分组,并绘制出了部分频率分布直方图如图所示.
(1)请将频率分布直方图补充完整;
(2)估计样本中所有用户的平均年龄(同一组中的数据用该组区间的中间值作代表);
(3)销售部从年龄在[20,30),[30,40)两组的样本中用比例分配的分层随机抽样方法抽取4人,再从这4人中随机抽取2人进行电话回访,求这2人取自不同年龄区间的概率.
18.(2025春 七里河区校级期中)某电子商务公司对10000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)求直方图中的a的值;
(2)估计这10000名网络购物者在2017年度的消费的中位数和平均数.
19.(2025 泰安模拟)某AI大模型想象力引擎处理用户问题分为“深度思考”模式和“联网搜索”模式,用户可根据需求在提问时自由选择.据统计,人们在使用该大模型时,有30%的问题选择“深度思考”模式,70%的问题选择“联网搜索”模式.而在选择“深度思考”模式的问题中40%被检测到包含“科幻”关键词(S),在选择“联网搜索”模式的问题中10%被检测到包含“科幻”关键词(S).以下记录了5次该大模型回答用户问题的处理时间(单位:分钟)、问题字数(单位:百字)和需求模式的相关数据:
问题 字数(百字) 需求模式 处理时间(分钟)
1 2.0 深度思考 5.0
2 1.5 联网搜索 3.0
3 3.0 深度思考 7.0
4 2.5 联网搜索 4.5
5 4.0 深度思考 8.4
(1)用频率估计概率.
①求问题被检测到包含“科幻”关键词(S)的概率;
②当问题被检测到包含“科幻”关键词(S)时,求用户选择“深度思考”模式的概率;
(2)假设在“深度思考”模式下,处理时间y关于字数x呈线性相关.请预测“深度思考”模式下,处理一个350字用户问题的时间.
(参考公式,)
20.(2025 宁夏二模)某制药厂生产一种治疗流感的药物,该药品有效成分的标准含量为10mg/片.由于升级了生产工艺,需检验采用新工艺生产的药品的有效成分是否达标,现随机抽取了生产的10片药品作为样本,测得其有效成分含量如下:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1.
(1)计算样本的平均数和方差s2;
(2)判断采用新工艺生产的药品的有效成分是否达标(若|10|>3.25,则认为采用新工艺生产的药品的有效成分不达标;反之认为达标)
高考数学一轮复习 统计
参考答案与试题解析
一.选择题(共8小题)
1.(2025春 商丘期末)已知两个变量x与y对应关系如下表:
x 1 2 3 4 5
y 5 7.5 n 9 10.5
若y与x满足线性相关关系,且经验回归方程为,则下列说法正确的是( ).
A.y与x正相关
B.在x=4处的残差为0.25
C.n=8.5
D.变量x每增加一个单位,y的值一定增加1.25个单位
【考点】经验回归方程与经验回归直线.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】A
【分析】根据回归直线一次项系数判断A;计算残差判断B;利用样本中心在回归直线上求参数判断C;由回归直线的实际意义判断D.
【解答】解:由回归直线的斜率为1.25>0,可知y与x正相关,故A正确;
当x=4时,,所以在x=4处的残差为9﹣9.25=﹣0.25,故B错误;
因为,所以,
则5+7.5+n+9+10.5=5×8,解得n=8,故C错误;
变量x每增加一个单位,y的值很大可能增加1.25个单位,故D错误.
故选:A.
【点评】本题考查经验回归方程及其应用,是基础题.
2.(2025春 郑州期末)数据5,7,3,2,11,13的第70百分位数为( )
A.7 B.11 C.13 D.17
【考点】百分位数.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】B
【分析】直接例用百分位数的定义求法.
【解答】解:数据5,7,3,2,11,13从小到大依次为2,3,5,7,11,13,
由6×70%=4.2,可知该组数据的第70百分位数是第5个数,为11.
故选:B.
【点评】本题考查百分位数的求法,是基础题.
3.(2025春 怀化期末)某同学8次考试的数学成绩从低到高分别为85,87,89,9θ,92,93,94,96,则这组成绩的75%分位数为( )
A.88 B.93 C.93.5 D.94
【考点】百分位数.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】C
【分析】直接利用百分位数的定义求解即可.
【解答】解:数据85,87,89,9θ,92,93,94,96共6个数,且从小到大排列,
由于8×75%=6,所以这组成绩的75%分位数为第6与第7个数的平均数,等.
故选:C.
【点评】本题考查百分位数的求法,是基础题.
4.(2025 山东校级模拟)高二(1)班有40名学生,其中男生有16名,已知男生平均体重为68.4kg,总平均体重为60.1kg,则女生的平均体重约为( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
【考点】平均数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据题意,设女生的平均体重为x,分析可得68.4×16+24x=60×60.1,解可得答案.
【解答】解:根据题意,设女生的平均体重为x,
高二(1)班有40名学生,其中男生有16名,则女生有40﹣16=24名,
已知男生平均体重为68.4kg,总平均体重为60.1kg,则有68.4×16+24x=60×60.1,
解可得:x≈54.6,即女生的平均体重约为54.6kg.
故选:B.
【点评】本题考查平均数的计算,注意总体平均数的计算,属于基础题.
5.(2025 靖远县校级模拟)某社会实践基地,在实践结束后对学生进行考核评分,某班学生得分的条形图如图所示,则该班学生成绩的75%分位数为( )
A.79 B.83 C.87 D.88
【考点】百分位数.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】先计算出频数,再根据计算一组n个数据的第p百分位数的步骤计算即可.
【解答】解:由题意可知知0.75×20=15,故该班成绩的75%分位数为第15项与第16项的和的平均数,
由直方图可知第15,1项分别为79,87,
故该班成绩的75%分位数为.
故选:B.
【点评】本题考查了百分位数的求解,属于基础题.
6.(2025 安顺模拟)平均数、中位数和众数都是刻画一组数据的集中趋势的信息,它们的大小关系和数据分布的形态有关在如图分布形态中,a,b,c分别对应这组数据的平均数、中位数和众数,则下列关系正确的是( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
【考点】平均数;中位数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】A
【分析】利用数据分布图左拖尾,即平均数小于中位数,再利用众数是用最高矩形的中点值来估计,可判断众数大于中位数,即可作出判断.
【解答】解:根据题意,由数据分布图知,
数据的众数为c,众数是最高矩形下底边的中点横坐标,因此众数c为右起第二个矩形下底边的中点值,
数据的中位数为b,直线x=b左右两边矩形面积相等,而直线x=c左边矩形面积大于右边矩形面积,则b<c,
数据的平均数为a,由于数据分布图左拖尾,则平均数a小于中位数b,即a<b,
所以a<b<c.
故选:A.
【点评】本题考查由数据分布图分析数据,注意平均数、中位数、众数的定义,属于基础题.
7.(2025春 青秀区校级月考)某学校有高中学生1000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380,为了调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,那么应抽取高二年级学生的人数为( )
A.50 B.60 C.70 D.80
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】B
【分析】根据分层抽样原则直接求解即可.
【解答】解:采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,
那么应抽取高二年级学生的人数为.
故选:B.
【点评】本题考查分层抽样的应用,属于基础题.
8.(2025春 浦东新区校级期末)为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据如表可得回归直线方程x,其中0.78,,据此估计,该社区一户收入为16万元家庭年支出为( )
收入x万 8.3 8.6 9.9 11.1 12.1
支出y万 5.9 7.8 8.1 8.4 9.8
A.12.68万元 B.13.88万元 C.12.78万元 D.14.28万元
【考点】经验回归方程与经验回归直线.
【专题】方程思想;综合法;概率与统计;运算求解.
【答案】A
【分析】由表格中的数据可求出,再根据,求出,从而得到线性回归方程为,再把x=16代入回归方程即可得解.
【解答】解:由表中的数据可知,,
,
因为0.78,,所以,
所以,
当x=16时,.
故选:A.
【点评】本题考查线性回归方程,考查学生数据分析能力和运算能力,属于基础题.
二.多选题(共4小题)
(多选)9.(2025春 温州期末)某电商平台决定对会员进行满意度调查.该平台共有2000名会员,其中女性会员1500人,男性会员500人,采用等比例分层随机抽样的方法抽取容量为80的样本.经计算得女性样本的满意度平均数为9,方差为2,男性样本的满意度平均数为8,方差为1,则( )
A.男性会员的样本容量为40
B.每位会员被抽到的概率为
C.估计该平台会员的满意度平均数为8.75
D.估计该平台会员满意度的方差为
【考点】方差.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】BCD
【分析】结合样本容量的定义,平均数、方差的公式,即可求解.
【解答】解:选项A:等比例分层抽样中,男性样本容量为,故A错误;
选项B:每位会员被抽到的概率为,故B正确;
选项C:总体满意度平均数估计为各层平均数按比例加权平均,女性占比,男性占比,则总体平均数为,故C正确;
选项D:总体方差估计需计算各层方差与层间差异的加权和.
设总体平均数μ=8.75,
男性层:比例,方差,平均数,
则,贡献为,
女性层:比例,方差,平均数,
则,贡献为;
总体方差为,故D正确.
故选:BCD.
【点评】本题主要考查样本容量的定义,平均数、方差的公式,属于基础题.
(多选)10.(2025春 无锡期末)对于数据2,6,8,3,3,4,6,8,下列说法正确的是( )
A.极差为6 B.平均数为5 C.没有众数 D.中位数为5
【考点】用样本估计总体的集中趋势参数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ABD
【分析】结合极差、众数、中位数的定义,以及平均数的公式,即可求解.
【解答】解:将数据进行排序:2,3,3,4,6,6,8,8,极差为8﹣2=6,故A正确;
平均数为(2+3+3+4+6+6+8)=5,故B正确;
众数为3,6,8,故C错误;
中位数为,故D正确.
故选:ABD.
【点评】本题主要考查极差、众数、中位数的定义,以及平均数的公式,是基础题.
(多选)11.(2025春 衢州期末)下列说法正确的是( )
A.数据2,3,4,5,6,7,8,9的第75百分位数为7
B.若一组样本数据3,a,7,5,4,8的极差为5,则实数a的取值范围为[3,8]
C.x1,x2,x3,x4和y1,y2,y3,y4的方差分别为和,若yi=2xi﹣3(i=1,2,3,4),则
D.在对高一某班学生数学成绩调查中,抽取男生10人,其平均数为105,方差为24,抽取女生5人,其平均数为102,方差为21,则这15名学生数学成绩的方差为25
【考点】百分位数;方差.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】BCD
【分析】对于A求出第75百分位数即可判断,对于B根据极差的定义即可判断,对于C根据方差的性质即可判断,对于D计算分成抽样的方差即可判断.
【解答】解:数据2,3,4,5,6,7,8,9,
由8×75%=6,所以第75百分位数为,故A错误;
若一组样本数据3,a,7,5,4,8的极差为5,所以3≤a≤8,故B正确;
若yi=2xi﹣3(i=1,2,3,4),即,故C正确;
,抽取男生10人,其平均数为105,抽取女生5人,其平均数为102,
则这15名学生数学成绩的平均数为,
所以这15名学生数学成绩的方差为,故D正确.
故选:BCD.
【点评】本题主要考查概率、统计的知识,属于基础题.
(多选)12.(2025春 西秀区校级期末)某校有高一学生n名,其中男生数与女生数之比为6:5,为了解学生的视力情况,现要求按分层抽样的方法抽取一个样本容量为的样本,若样本中男生比女生多12人,则下列结论正确的是( )
A.样本中有60名女生 B.样本容量为132
C.高一学生共有1430人 D.高一有720名男生
【考点】分层随机抽样.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ABD
【分析】根据已知条件,结合分层抽样的定义,即可求解.
【解答】解:某校有高一学生n名,其中男生数与女生数之比为6:5,样本中男生比女生多12人,
则,解得n=1320,故C错误;
样本容量为,故B正确;
高一有男生,故D正确;
抽取了名女生,故A正确.
故选:ABD.
【点评】本题主要考查分层抽样的定义,属于基础题.
三.填空题(共4小题)
13.(2025春 徐汇区期末)对学校高三年级某班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若高校A专业对视力要求不低于0.9,则该班学生中有 20 人能报考该专业.
【考点】频率分布直方图.
【专题】数形结合;数形结合法;概率与统计;运算求解.
【答案】20.
【分析】先求得视力在0.9以上的频率,再根据频数、频率、样本容量的关系即可求得答案.
【解答】解:由频率分布直方图知:视力在0.9以上的频率为(1.00+0.75+0.25)×0.2=0.4,
所以该班学生中有50×0.4=20人能报考该专业.
故答案为:20.
【点评】本题考查频率分布直方图,属于基础题.
14.(2025春 舟山期末)有一组数据:5,7,10,9,8.则其第60百分位数为 8.5 .
【考点】百分位数.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】8.5.
【分析】先将这组数据由小到大进行排序,再结合百分位数的定义求解即可.
【解答】解:将这组数据由小到大依次排序为:5,7,8,9,10,
共有5个数据,所以5×60%=3,
则这组数据的第60百分位数为8.5.
故答案为:8.5.
【点评】本题考查百分位数的求解,属于基础题.
15.(2025春 徐汇区期末)某校高中一年级共有男生204名,女生221名.徐老师为了解该校高一年级学生的身高情况,采用分层抽样的方法,随机抽出男生24名,女生n名,则n的值为 26 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;定义法;概率与统计;运算求解.
【答案】26.
【分析】利用抽样比相等可求n的值.
【解答】解:由已知可得.
故答案为:26.
【点评】本题考查分层抽样,属于基础题.
16.(2025春 红桥区校级月考)采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,则这个学校共有高中学生 1600 人.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】1600.
【分析】首先求出高三年级抽取的人数,再根据抽样比即可求出总人数.
【解答】解:采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,
可得高三年级共抽取80﹣20﹣30=30人,
又高三年级共有600人,所以抽样比为,
所以学校共有高中生人.
故答案为:1600.
【点评】本题主要考查分层抽样的应用,属于基础题.
四.解答题(共4小题)
17.(2025春 环县校级期末)今年“双碳”再次成为全国两会的热点词汇.“双碳”即我国提出力争2030年前实现碳达峰,2060年前实现碳中和.低碳生活引领生活时尚,新能源汽车成为当前购车的首选.某新能源汽车销售部为了满足广大客户对新能源汽车性能的需求,随机抽取了500名用户进行问卷调查,根据统计情况,将他们的年龄按[20,30),[30,40),[40,50),[50,60),[60,70]分组,并绘制出了部分频率分布直方图如图所示.
(1)请将频率分布直方图补充完整;
(2)估计样本中所有用户的平均年龄(同一组中的数据用该组区间的中间值作代表);
(3)销售部从年龄在[20,30),[30,40)两组的样本中用比例分配的分层随机抽样方法抽取4人,再从这4人中随机抽取2人进行电话回访,求这2人取自不同年龄区间的概率.
【考点】补全频率分布直方图.
【专题】应用题;数形结合;分析法;概率与统计;数据分析.
【答案】(1)答案见解析;
(2)45岁;
(3).
【分析】(1)根据频率分布直方图计算缺少的部分的频率,再补充频率分布直方图即可;
(2)利用频率分布直方图中平均数估计的计算公式计算即可;
(3)根据分层抽样,计算年龄在[20,30)内的有1人,记为A;年龄在[30,40)内的有3人,分别记为 B1,B2,B3,由列举法及古典概型的计算公式计算可得答案.
【解答】解:(1)年龄在[30,40)的频率为1﹣(0.008+0.040+0.016+0.012)×10=0.24,补充完整的频率分布直方图如下图:
(2)所有用户的平均年龄的估计值为10×(0.008×25+0.024×35+0.040×45+0.016×55+0.012×65)=45,故估计样本中所有用户的平均年龄为45岁;
(3)由分层随机抽样的方法可知,抽取的4人中,年龄在[20,30)内的有1人,记为A;
年龄在[30,40)内的有3人,分别记为 B1,B2,B3,
则从这4人中随机抽取2人的所有基本事件有 (A,B1),(A,B2),(A,B3),(B1,B2),( B1,B3),(B2,B3) 共6种;
记这2人取自不同年龄区间为事件M,其基本事件有 (A,B1),(A,B2),(A,B3),共3种,
故这2人取自不同年龄区间的概率为.
【点评】本题考查频率分布直方图的性质和古典概率模型,属于基础题.
18.(2025春 七里河区校级期中)某电子商务公司对10000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)求直方图中的a的值;
(2)估计这10000名网络购物者在2017年度的消费的中位数和平均数.
【考点】补全频率分布直方图.
【专题】数形结合;定义法;概率与统计;运算求解.
【答案】(1)a=3.
(2)中位数为,平均数为0.537.
【分析】(1)由频率分布直方图的性质列方程能求出a.
(2)由频率分布直方图的性质能求出中位数和平均数.
【解答】解:(1)由频率分布直方图的性质得:
0.02+0.08+0.15+0.2+0.25+0.1a=1,
解得a=3.
(2)0.5﹣0.15﹣0.25=0.1,
∴中位数为:,
平均数:0.35×0.15+0.45×0.25+0.55×0.3+0.65×0.2+0.75×0.08+0.85×0.02=0.537.
【点评】本题考查频率分布直方图、中位数、平均数等基础知识,考查运算求解能力,是基础题.
19.(2025 泰安模拟)某AI大模型想象力引擎处理用户问题分为“深度思考”模式和“联网搜索”模式,用户可根据需求在提问时自由选择.据统计,人们在使用该大模型时,有30%的问题选择“深度思考”模式,70%的问题选择“联网搜索”模式.而在选择“深度思考”模式的问题中40%被检测到包含“科幻”关键词(S),在选择“联网搜索”模式的问题中10%被检测到包含“科幻”关键词(S).以下记录了5次该大模型回答用户问题的处理时间(单位:分钟)、问题字数(单位:百字)和需求模式的相关数据:
问题 字数(百字) 需求模式 处理时间(分钟)
1 2.0 深度思考 5.0
2 1.5 联网搜索 3.0
3 3.0 深度思考 7.0
4 2.5 联网搜索 4.5
5 4.0 深度思考 8.4
(1)用频率估计概率.
①求问题被检测到包含“科幻”关键词(S)的概率;
②当问题被检测到包含“科幻”关键词(S)时,求用户选择“深度思考”模式的概率;
(2)假设在“深度思考”模式下,处理时间y关于字数x呈线性相关.请预测“深度思考”模式下,处理一个350字用户问题的时间.
(参考公式,)
【考点】一元线性回归模型.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)①0.19;②;
(2)7.65分钟.
【分析】(1)①根据给定条件,利用全概率公式列式计算;②由①,利用条件概率公式计算得解.
(2)利用最小二乘法公式求出回归方程,再求出处理问题时间的估计值.
【解答】解:(1)①记事件A=“选择深度思考模式”,事件B=“被检测到包含科幻关键词(S)”,
则,,
由全概率公式得,
所以问题被检测到包含“科幻”关键词(S)的概率为0.19;
②由①得,
所以用户选择“深度思考”模式的概率为;
(2)依题意,,
,
则,,
因此处理时间y关于字数x的回归方程为,
当x=3.5时,(分钟),
所以处理一个350字用户问题的时间约为7.65分钟.
【点评】本题考查了回归方程,属于中档题.
20.(2025 宁夏二模)某制药厂生产一种治疗流感的药物,该药品有效成分的标准含量为10mg/片.由于升级了生产工艺,需检验采用新工艺生产的药品的有效成分是否达标,现随机抽取了生产的10片药品作为样本,测得其有效成分含量如下:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1.
(1)计算样本的平均数和方差s2;
(2)判断采用新工艺生产的药品的有效成分是否达标(若|10|>3.25,则认为采用新工艺生产的药品的有效成分不达标;反之认为达标)
【考点】方差;平均数.
【专题】计算题;方程思想;综合法;概率与统计;运算求解.
【答案】(1)平均数9.9,方差s2=0.04;
(2)达标.
【分析】(1)根据题意,由平均数和方差公式计算可得答案;
(2)根据题意,计算并比较|10|和3.25的大小,即可得结论.
【解答】解:(1)根据题意,样本数据为:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1,
则其平均数(9.7+10+9.7+9.6+9.7+9.9+10.2+10.1+10+10.1)=9.9mg,
其方差S2(0.04+0.01+0.04+0.09+0.04+0+0.09+0.04+0.01+0.04)=0.04,
(2)根据题意,由(1)的结论,样本的平均数9.9,方差s2=0.04,
则有|10|=0.1,而3.25,
则有|10|<3.25,故采用新工艺生产的药品的有效成分达标.
【点评】本题考查数据平均数、方差的计算公式,注意平均数、方差的计算公式,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
高考数学一轮复习 统计
一.选择题(共8小题)
1.(2025春 商丘期末)已知两个变量x与y对应关系如下表:
x 1 2 3 4 5
y 5 7.5 n 9 10.5
若y与x满足线性相关关系,且经验回归方程为,则下列说法正确的是( ).
A.y与x正相关
B.在x=4处的残差为0.25
C.n=8.5
D.变量x每增加一个单位,y的值一定增加1.25个单位
2.(2025春 郑州期末)数据5,7,3,2,11,13的第70百分位数为( )
A.7 B.11 C.13 D.17
3.(2025春 怀化期末)某同学8次考试的数学成绩从低到高分别为85,87,89,9θ,92,93,94,96,则这组成绩的75%分位数为( )
A.88 B.93 C.93.5 D.94
4.(2025 山东校级模拟)高二(1)班有40名学生,其中男生有16名,已知男生平均体重为68.4kg,总平均体重为60.1kg,则女生的平均体重约为( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
5.(2025 靖远县校级模拟)某社会实践基地,在实践结束后对学生进行考核评分,某班学生得分的条形图如图所示,则该班学生成绩的75%分位数为( )
A.79 B.83 C.87 D.88
6.(2025 安顺模拟)平均数、中位数和众数都是刻画一组数据的集中趋势的信息,它们的大小关系和数据分布的形态有关在如图分布形态中,a,b,c分别对应这组数据的平均数、中位数和众数,则下列关系正确的是( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
7.(2025春 青秀区校级月考)某学校有高中学生1000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380,为了调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,那么应抽取高二年级学生的人数为( )
A.50 B.60 C.70 D.80
8.(2025春 浦东新区校级期末)为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据如表可得回归直线方程x,其中0.78,,据此估计,该社区一户收入为16万元家庭年支出为( )
收入x万 8.3 8.6 9.9 11.1 12.1
支出y万 5.9 7.8 8.1 8.4 9.8
A.12.68万元 B.13.88万元 C.12.78万元 D.14.28万元
二.多选题(共4小题)
(多选)9.(2025春 温州期末)某电商平台决定对会员进行满意度调查.该平台共有2000名会员,其中女性会员1500人,男性会员500人,采用等比例分层随机抽样的方法抽取容量为80的样本.经计算得女性样本的满意度平均数为9,方差为2,男性样本的满意度平均数为8,方差为1,则( )
A.男性会员的样本容量为40
B.每位会员被抽到的概率为
C.估计该平台会员的满意度平均数为8.75
D.估计该平台会员满意度的方差为
(多选)10.(2025春 无锡期末)对于数据2,6,8,3,3,4,6,8,下列说法正确的是( )
A.极差为6 B.平均数为5 C.没有众数 D.中位数为5
(多选)11.(2025春 衢州期末)下列说法正确的是( )
A.数据2,3,4,5,6,7,8,9的第75百分位数为7
B.若一组样本数据3,a,7,5,4,8的极差为5,则实数a的取值范围为[3,8]
C.x1,x2,x3,x4和y1,y2,y3,y4的方差分别为和,若yi=2xi﹣3(i=1,2,3,4),则
D.在对高一某班学生数学成绩调查中,抽取男生10人,其平均数为105,方差为24,抽取女生5人,其平均数为102,方差为21,则这15名学生数学成绩的方差为25
(多选)12.(2025春 西秀区校级期末)某校有高一学生n名,其中男生数与女生数之比为6:5,为了解学生的视力情况,现要求按分层抽样的方法抽取一个样本容量为的样本,若样本中男生比女生多12人,则下列结论正确的是( )
A.样本中有60名女生 B.样本容量为132
C.高一学生共有1430人 D.高一有720名男生
三.填空题(共4小题)
13.(2025春 徐汇区期末)对学校高三年级某班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若高校A专业对视力要求不低于0.9,则该班学生中有 人能报考该专业.
14.(2025春 舟山期末)有一组数据:5,7,10,9,8.则其第60百分位数为 .
15.(2025春 徐汇区期末)某校高中一年级共有男生204名,女生221名.徐老师为了解该校高一年级学生的身高情况,采用分层抽样的方法,随机抽出男生24名,女生n名,则n的值为 .
16.(2025春 红桥区校级月考)采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,则这个学校共有高中学生 人.
四.解答题(共4小题)
17.(2025春 环县校级期末)今年“双碳”再次成为全国两会的热点词汇.“双碳”即我国提出力争2030年前实现碳达峰,2060年前实现碳中和.低碳生活引领生活时尚,新能源汽车成为当前购车的首选.某新能源汽车销售部为了满足广大客户对新能源汽车性能的需求,随机抽取了500名用户进行问卷调查,根据统计情况,将他们的年龄按[20,30),[30,40),[40,50),[50,60),[60,70]分组,并绘制出了部分频率分布直方图如图所示.
(1)请将频率分布直方图补充完整;
(2)估计样本中所有用户的平均年龄(同一组中的数据用该组区间的中间值作代表);
(3)销售部从年龄在[20,30),[30,40)两组的样本中用比例分配的分层随机抽样方法抽取4人,再从这4人中随机抽取2人进行电话回访,求这2人取自不同年龄区间的概率.
18.(2025春 七里河区校级期中)某电子商务公司对10000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)求直方图中的a的值;
(2)估计这10000名网络购物者在2017年度的消费的中位数和平均数.
19.(2025 泰安模拟)某AI大模型想象力引擎处理用户问题分为“深度思考”模式和“联网搜索”模式,用户可根据需求在提问时自由选择.据统计,人们在使用该大模型时,有30%的问题选择“深度思考”模式,70%的问题选择“联网搜索”模式.而在选择“深度思考”模式的问题中40%被检测到包含“科幻”关键词(S),在选择“联网搜索”模式的问题中10%被检测到包含“科幻”关键词(S).以下记录了5次该大模型回答用户问题的处理时间(单位:分钟)、问题字数(单位:百字)和需求模式的相关数据:
问题 字数(百字) 需求模式 处理时间(分钟)
1 2.0 深度思考 5.0
2 1.5 联网搜索 3.0
3 3.0 深度思考 7.0
4 2.5 联网搜索 4.5
5 4.0 深度思考 8.4
(1)用频率估计概率.
①求问题被检测到包含“科幻”关键词(S)的概率;
②当问题被检测到包含“科幻”关键词(S)时,求用户选择“深度思考”模式的概率;
(2)假设在“深度思考”模式下,处理时间y关于字数x呈线性相关.请预测“深度思考”模式下,处理一个350字用户问题的时间.
(参考公式,)
20.(2025 宁夏二模)某制药厂生产一种治疗流感的药物,该药品有效成分的标准含量为10mg/片.由于升级了生产工艺,需检验采用新工艺生产的药品的有效成分是否达标,现随机抽取了生产的10片药品作为样本,测得其有效成分含量如下:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1.
(1)计算样本的平均数和方差s2;
(2)判断采用新工艺生产的药品的有效成分是否达标(若|10|>3.25,则认为采用新工艺生产的药品的有效成分不达标;反之认为达标)
高考数学一轮复习 统计
参考答案与试题解析
一.选择题(共8小题)
1.(2025春 商丘期末)已知两个变量x与y对应关系如下表:
x 1 2 3 4 5
y 5 7.5 n 9 10.5
若y与x满足线性相关关系,且经验回归方程为,则下列说法正确的是( ).
A.y与x正相关
B.在x=4处的残差为0.25
C.n=8.5
D.变量x每增加一个单位,y的值一定增加1.25个单位
【考点】经验回归方程与经验回归直线.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】A
【分析】根据回归直线一次项系数判断A;计算残差判断B;利用样本中心在回归直线上求参数判断C;由回归直线的实际意义判断D.
【解答】解:由回归直线的斜率为1.25>0,可知y与x正相关,故A正确;
当x=4时,,所以在x=4处的残差为9﹣9.25=﹣0.25,故B错误;
因为,所以,
则5+7.5+n+9+10.5=5×8,解得n=8,故C错误;
变量x每增加一个单位,y的值很大可能增加1.25个单位,故D错误.
故选:A.
【点评】本题考查经验回归方程及其应用,是基础题.
2.(2025春 郑州期末)数据5,7,3,2,11,13的第70百分位数为( )
A.7 B.11 C.13 D.17
【考点】百分位数.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】B
【分析】直接例用百分位数的定义求法.
【解答】解:数据5,7,3,2,11,13从小到大依次为2,3,5,7,11,13,
由6×70%=4.2,可知该组数据的第70百分位数是第5个数,为11.
故选:B.
【点评】本题考查百分位数的求法,是基础题.
3.(2025春 怀化期末)某同学8次考试的数学成绩从低到高分别为85,87,89,9θ,92,93,94,96,则这组成绩的75%分位数为( )
A.88 B.93 C.93.5 D.94
【考点】百分位数.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】C
【分析】直接利用百分位数的定义求解即可.
【解答】解:数据85,87,89,9θ,92,93,94,96共6个数,且从小到大排列,
由于8×75%=6,所以这组成绩的75%分位数为第6与第7个数的平均数,等.
故选:C.
【点评】本题考查百分位数的求法,是基础题.
4.(2025 山东校级模拟)高二(1)班有40名学生,其中男生有16名,已知男生平均体重为68.4kg,总平均体重为60.1kg,则女生的平均体重约为( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
【考点】平均数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据题意,设女生的平均体重为x,分析可得68.4×16+24x=60×60.1,解可得答案.
【解答】解:根据题意,设女生的平均体重为x,
高二(1)班有40名学生,其中男生有16名,则女生有40﹣16=24名,
已知男生平均体重为68.4kg,总平均体重为60.1kg,则有68.4×16+24x=60×60.1,
解可得:x≈54.6,即女生的平均体重约为54.6kg.
故选:B.
【点评】本题考查平均数的计算,注意总体平均数的计算,属于基础题.
5.(2025 靖远县校级模拟)某社会实践基地,在实践结束后对学生进行考核评分,某班学生得分的条形图如图所示,则该班学生成绩的75%分位数为( )
A.79 B.83 C.87 D.88
【考点】百分位数.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】先计算出频数,再根据计算一组n个数据的第p百分位数的步骤计算即可.
【解答】解:由题意可知知0.75×20=15,故该班成绩的75%分位数为第15项与第16项的和的平均数,
由直方图可知第15,1项分别为79,87,
故该班成绩的75%分位数为.
故选:B.
【点评】本题考查了百分位数的求解,属于基础题.
6.(2025 安顺模拟)平均数、中位数和众数都是刻画一组数据的集中趋势的信息,它们的大小关系和数据分布的形态有关在如图分布形态中,a,b,c分别对应这组数据的平均数、中位数和众数,则下列关系正确的是( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
【考点】平均数;中位数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】A
【分析】利用数据分布图左拖尾,即平均数小于中位数,再利用众数是用最高矩形的中点值来估计,可判断众数大于中位数,即可作出判断.
【解答】解:根据题意,由数据分布图知,
数据的众数为c,众数是最高矩形下底边的中点横坐标,因此众数c为右起第二个矩形下底边的中点值,
数据的中位数为b,直线x=b左右两边矩形面积相等,而直线x=c左边矩形面积大于右边矩形面积,则b<c,
数据的平均数为a,由于数据分布图左拖尾,则平均数a小于中位数b,即a<b,
所以a<b<c.
故选:A.
【点评】本题考查由数据分布图分析数据,注意平均数、中位数、众数的定义,属于基础题.
7.(2025春 青秀区校级月考)某学校有高中学生1000人,其中高一年级、高二年级、高三年级的人数分别为320,300,380,为了调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,那么应抽取高二年级学生的人数为( )
A.50 B.60 C.70 D.80
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】整体思想;定义法;概率与统计;运算求解.
【答案】B
【分析】根据分层抽样原则直接求解即可.
【解答】解:采用分层抽样的方法从该校学生中抽取一个样本量为200的样本,
那么应抽取高二年级学生的人数为.
故选:B.
【点评】本题考查分层抽样的应用,属于基础题.
8.(2025春 浦东新区校级期末)为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据如表可得回归直线方程x,其中0.78,,据此估计,该社区一户收入为16万元家庭年支出为( )
收入x万 8.3 8.6 9.9 11.1 12.1
支出y万 5.9 7.8 8.1 8.4 9.8
A.12.68万元 B.13.88万元 C.12.78万元 D.14.28万元
【考点】经验回归方程与经验回归直线.
【专题】方程思想;综合法;概率与统计;运算求解.
【答案】A
【分析】由表格中的数据可求出,再根据,求出,从而得到线性回归方程为,再把x=16代入回归方程即可得解.
【解答】解:由表中的数据可知,,
,
因为0.78,,所以,
所以,
当x=16时,.
故选:A.
【点评】本题考查线性回归方程,考查学生数据分析能力和运算能力,属于基础题.
二.多选题(共4小题)
(多选)9.(2025春 温州期末)某电商平台决定对会员进行满意度调查.该平台共有2000名会员,其中女性会员1500人,男性会员500人,采用等比例分层随机抽样的方法抽取容量为80的样本.经计算得女性样本的满意度平均数为9,方差为2,男性样本的满意度平均数为8,方差为1,则( )
A.男性会员的样本容量为40
B.每位会员被抽到的概率为
C.估计该平台会员的满意度平均数为8.75
D.估计该平台会员满意度的方差为
【考点】方差.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】BCD
【分析】结合样本容量的定义,平均数、方差的公式,即可求解.
【解答】解:选项A:等比例分层抽样中,男性样本容量为,故A错误;
选项B:每位会员被抽到的概率为,故B正确;
选项C:总体满意度平均数估计为各层平均数按比例加权平均,女性占比,男性占比,则总体平均数为,故C正确;
选项D:总体方差估计需计算各层方差与层间差异的加权和.
设总体平均数μ=8.75,
男性层:比例,方差,平均数,
则,贡献为,
女性层:比例,方差,平均数,
则,贡献为;
总体方差为,故D正确.
故选:BCD.
【点评】本题主要考查样本容量的定义,平均数、方差的公式,属于基础题.
(多选)10.(2025春 无锡期末)对于数据2,6,8,3,3,4,6,8,下列说法正确的是( )
A.极差为6 B.平均数为5 C.没有众数 D.中位数为5
【考点】用样本估计总体的集中趋势参数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ABD
【分析】结合极差、众数、中位数的定义,以及平均数的公式,即可求解.
【解答】解:将数据进行排序:2,3,3,4,6,6,8,8,极差为8﹣2=6,故A正确;
平均数为(2+3+3+4+6+6+8)=5,故B正确;
众数为3,6,8,故C错误;
中位数为,故D正确.
故选:ABD.
【点评】本题主要考查极差、众数、中位数的定义,以及平均数的公式,是基础题.
(多选)11.(2025春 衢州期末)下列说法正确的是( )
A.数据2,3,4,5,6,7,8,9的第75百分位数为7
B.若一组样本数据3,a,7,5,4,8的极差为5,则实数a的取值范围为[3,8]
C.x1,x2,x3,x4和y1,y2,y3,y4的方差分别为和,若yi=2xi﹣3(i=1,2,3,4),则
D.在对高一某班学生数学成绩调查中,抽取男生10人,其平均数为105,方差为24,抽取女生5人,其平均数为102,方差为21,则这15名学生数学成绩的方差为25
【考点】百分位数;方差.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】BCD
【分析】对于A求出第75百分位数即可判断,对于B根据极差的定义即可判断,对于C根据方差的性质即可判断,对于D计算分成抽样的方差即可判断.
【解答】解:数据2,3,4,5,6,7,8,9,
由8×75%=6,所以第75百分位数为,故A错误;
若一组样本数据3,a,7,5,4,8的极差为5,所以3≤a≤8,故B正确;
若yi=2xi﹣3(i=1,2,3,4),即,故C正确;
,抽取男生10人,其平均数为105,抽取女生5人,其平均数为102,
则这15名学生数学成绩的平均数为,
所以这15名学生数学成绩的方差为,故D正确.
故选:BCD.
【点评】本题主要考查概率、统计的知识,属于基础题.
(多选)12.(2025春 西秀区校级期末)某校有高一学生n名,其中男生数与女生数之比为6:5,为了解学生的视力情况,现要求按分层抽样的方法抽取一个样本容量为的样本,若样本中男生比女生多12人,则下列结论正确的是( )
A.样本中有60名女生 B.样本容量为132
C.高一学生共有1430人 D.高一有720名男生
【考点】分层随机抽样.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ABD
【分析】根据已知条件,结合分层抽样的定义,即可求解.
【解答】解:某校有高一学生n名,其中男生数与女生数之比为6:5,样本中男生比女生多12人,
则,解得n=1320,故C错误;
样本容量为,故B正确;
高一有男生,故D正确;
抽取了名女生,故A正确.
故选:ABD.
【点评】本题主要考查分层抽样的定义,属于基础题.
三.填空题(共4小题)
13.(2025春 徐汇区期末)对学校高三年级某班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若高校A专业对视力要求不低于0.9,则该班学生中有 20 人能报考该专业.
【考点】频率分布直方图.
【专题】数形结合;数形结合法;概率与统计;运算求解.
【答案】20.
【分析】先求得视力在0.9以上的频率,再根据频数、频率、样本容量的关系即可求得答案.
【解答】解:由频率分布直方图知:视力在0.9以上的频率为(1.00+0.75+0.25)×0.2=0.4,
所以该班学生中有50×0.4=20人能报考该专业.
故答案为:20.
【点评】本题考查频率分布直方图,属于基础题.
14.(2025春 舟山期末)有一组数据:5,7,10,9,8.则其第60百分位数为 8.5 .
【考点】百分位数.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】8.5.
【分析】先将这组数据由小到大进行排序,再结合百分位数的定义求解即可.
【解答】解:将这组数据由小到大依次排序为:5,7,8,9,10,
共有5个数据,所以5×60%=3,
则这组数据的第60百分位数为8.5.
故答案为:8.5.
【点评】本题考查百分位数的求解,属于基础题.
15.(2025春 徐汇区期末)某校高中一年级共有男生204名,女生221名.徐老师为了解该校高一年级学生的身高情况,采用分层抽样的方法,随机抽出男生24名,女生n名,则n的值为 26 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;定义法;概率与统计;运算求解.
【答案】26.
【分析】利用抽样比相等可求n的值.
【解答】解:由已知可得.
故答案为:26.
【点评】本题考查分层抽样,属于基础题.
16.(2025春 红桥区校级月考)采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,则这个学校共有高中学生 1600 人.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】1600.
【分析】首先求出高三年级抽取的人数,再根据抽样比即可求出总人数.
【解答】解:采用分层抽样的方法抽取一个容量为80的样本,高一年级被抽取20人,高二年级被抽取30人,高三年级共有600人,
可得高三年级共抽取80﹣20﹣30=30人,
又高三年级共有600人,所以抽样比为,
所以学校共有高中生人.
故答案为:1600.
【点评】本题主要考查分层抽样的应用,属于基础题.
四.解答题(共4小题)
17.(2025春 环县校级期末)今年“双碳”再次成为全国两会的热点词汇.“双碳”即我国提出力争2030年前实现碳达峰,2060年前实现碳中和.低碳生活引领生活时尚,新能源汽车成为当前购车的首选.某新能源汽车销售部为了满足广大客户对新能源汽车性能的需求,随机抽取了500名用户进行问卷调查,根据统计情况,将他们的年龄按[20,30),[30,40),[40,50),[50,60),[60,70]分组,并绘制出了部分频率分布直方图如图所示.
(1)请将频率分布直方图补充完整;
(2)估计样本中所有用户的平均年龄(同一组中的数据用该组区间的中间值作代表);
(3)销售部从年龄在[20,30),[30,40)两组的样本中用比例分配的分层随机抽样方法抽取4人,再从这4人中随机抽取2人进行电话回访,求这2人取自不同年龄区间的概率.
【考点】补全频率分布直方图.
【专题】应用题;数形结合;分析法;概率与统计;数据分析.
【答案】(1)答案见解析;
(2)45岁;
(3).
【分析】(1)根据频率分布直方图计算缺少的部分的频率,再补充频率分布直方图即可;
(2)利用频率分布直方图中平均数估计的计算公式计算即可;
(3)根据分层抽样,计算年龄在[20,30)内的有1人,记为A;年龄在[30,40)内的有3人,分别记为 B1,B2,B3,由列举法及古典概型的计算公式计算可得答案.
【解答】解:(1)年龄在[30,40)的频率为1﹣(0.008+0.040+0.016+0.012)×10=0.24,补充完整的频率分布直方图如下图:
(2)所有用户的平均年龄的估计值为10×(0.008×25+0.024×35+0.040×45+0.016×55+0.012×65)=45,故估计样本中所有用户的平均年龄为45岁;
(3)由分层随机抽样的方法可知,抽取的4人中,年龄在[20,30)内的有1人,记为A;
年龄在[30,40)内的有3人,分别记为 B1,B2,B3,
则从这4人中随机抽取2人的所有基本事件有 (A,B1),(A,B2),(A,B3),(B1,B2),( B1,B3),(B2,B3) 共6种;
记这2人取自不同年龄区间为事件M,其基本事件有 (A,B1),(A,B2),(A,B3),共3种,
故这2人取自不同年龄区间的概率为.
【点评】本题考查频率分布直方图的性质和古典概率模型,属于基础题.
18.(2025春 七里河区校级期中)某电子商务公司对10000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)求直方图中的a的值;
(2)估计这10000名网络购物者在2017年度的消费的中位数和平均数.
【考点】补全频率分布直方图.
【专题】数形结合;定义法;概率与统计;运算求解.
【答案】(1)a=3.
(2)中位数为,平均数为0.537.
【分析】(1)由频率分布直方图的性质列方程能求出a.
(2)由频率分布直方图的性质能求出中位数和平均数.
【解答】解:(1)由频率分布直方图的性质得:
0.02+0.08+0.15+0.2+0.25+0.1a=1,
解得a=3.
(2)0.5﹣0.15﹣0.25=0.1,
∴中位数为:,
平均数:0.35×0.15+0.45×0.25+0.55×0.3+0.65×0.2+0.75×0.08+0.85×0.02=0.537.
【点评】本题考查频率分布直方图、中位数、平均数等基础知识,考查运算求解能力,是基础题.
19.(2025 泰安模拟)某AI大模型想象力引擎处理用户问题分为“深度思考”模式和“联网搜索”模式,用户可根据需求在提问时自由选择.据统计,人们在使用该大模型时,有30%的问题选择“深度思考”模式,70%的问题选择“联网搜索”模式.而在选择“深度思考”模式的问题中40%被检测到包含“科幻”关键词(S),在选择“联网搜索”模式的问题中10%被检测到包含“科幻”关键词(S).以下记录了5次该大模型回答用户问题的处理时间(单位:分钟)、问题字数(单位:百字)和需求模式的相关数据:
问题 字数(百字) 需求模式 处理时间(分钟)
1 2.0 深度思考 5.0
2 1.5 联网搜索 3.0
3 3.0 深度思考 7.0
4 2.5 联网搜索 4.5
5 4.0 深度思考 8.4
(1)用频率估计概率.
①求问题被检测到包含“科幻”关键词(S)的概率;
②当问题被检测到包含“科幻”关键词(S)时,求用户选择“深度思考”模式的概率;
(2)假设在“深度思考”模式下,处理时间y关于字数x呈线性相关.请预测“深度思考”模式下,处理一个350字用户问题的时间.
(参考公式,)
【考点】一元线性回归模型.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)①0.19;②;
(2)7.65分钟.
【分析】(1)①根据给定条件,利用全概率公式列式计算;②由①,利用条件概率公式计算得解.
(2)利用最小二乘法公式求出回归方程,再求出处理问题时间的估计值.
【解答】解:(1)①记事件A=“选择深度思考模式”,事件B=“被检测到包含科幻关键词(S)”,
则,,
由全概率公式得,
所以问题被检测到包含“科幻”关键词(S)的概率为0.19;
②由①得,
所以用户选择“深度思考”模式的概率为;
(2)依题意,,
,
则,,
因此处理时间y关于字数x的回归方程为,
当x=3.5时,(分钟),
所以处理一个350字用户问题的时间约为7.65分钟.
【点评】本题考查了回归方程,属于中档题.
20.(2025 宁夏二模)某制药厂生产一种治疗流感的药物,该药品有效成分的标准含量为10mg/片.由于升级了生产工艺,需检验采用新工艺生产的药品的有效成分是否达标,现随机抽取了生产的10片药品作为样本,测得其有效成分含量如下:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1.
(1)计算样本的平均数和方差s2;
(2)判断采用新工艺生产的药品的有效成分是否达标(若|10|>3.25,则认为采用新工艺生产的药品的有效成分不达标;反之认为达标)
【考点】方差;平均数.
【专题】计算题;方程思想;综合法;概率与统计;运算求解.
【答案】(1)平均数9.9,方差s2=0.04;
(2)达标.
【分析】(1)根据题意,由平均数和方差公式计算可得答案;
(2)根据题意,计算并比较|10|和3.25的大小,即可得结论.
【解答】解:(1)根据题意,样本数据为:9.7,10,9.7,9.6,9.7,9.9,10.2,10.1,10,10.1,
则其平均数(9.7+10+9.7+9.6+9.7+9.9+10.2+10.1+10+10.1)=9.9mg,
其方差S2(0.04+0.01+0.04+0.09+0.04+0+0.09+0.04+0.01+0.04)=0.04,
(2)根据题意,由(1)的结论,样本的平均数9.9,方差s2=0.04,
则有|10|=0.1,而3.25,
则有|10|<3.25,故采用新工艺生产的药品的有效成分达标.
【点评】本题考查数据平均数、方差的计算公式,注意平均数、方差的计算公式,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
