第八单元 立体几何与空间向量(二)(含解析)-《巅峰突破》2026版高中数学高三一轮复习
文档属性
| 名称 | 第八单元 立体几何与空间向量(二)(含解析)-《巅峰突破》2026版高中数学高三一轮复习 | 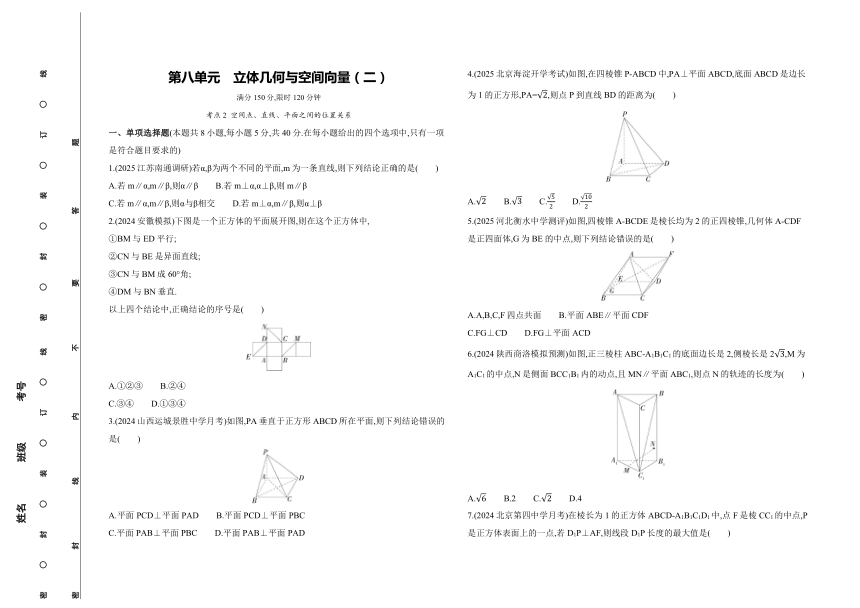 | |
| 格式 | docx | ||
| 文件大小 | 382.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 11:23:59 | ||
图片预览




文档简介
(
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第八单元 立体几何与空间向量(二)
满分150分,限时120分钟
考点2 空间点、直线、平面之间的位置关系
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2025江苏南通调研)若α,β为两个不同的平面,m为一条直线,则下列结论正确的是( )
A.若m∥α,m∥β,则α∥β B.若m⊥α,α⊥β,则m∥β
C.若m∥α,m∥β,则α与β相交 D.若m⊥α,m∥β,则α⊥β
2.(2024安徽模拟)下图是一个正方体的平面展开图,则在这个正方体中,
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个结论中,正确结论的序号是( )
A.①②③ B.②④
C.③④ D.①③④
3.(2024山西运城景胜中学月考)如图,PA垂直于正方形ABCD所在平面,则下列结论错误的是( )
A.平面PCD⊥平面PAD B.平面PCD⊥平面PBC
C.平面PAB⊥平面PBC D.平面PAB⊥平面PAD
4.(2025北京海淀开学考试)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的正方形,PA=,则点P到直线BD的距离为( )
A. B. C. D.
5.(2025河北衡水中学测评)如图,四棱锥A-BCDE是棱长均为2的正四棱锥,几何体A-CDF是正四面体,G为BE的中点,则下列结论错误的是( )
A.A,B,C,F四点共面 B.平面ABE∥平面CDF
C.FG⊥CD D.FG⊥平面ACD
6.(2024陕西商洛模拟预测)如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是2,M为A1C1的中点,N是侧面BCC1B1内的动点,且MN∥平面ABC1,则点N的轨迹的长度为( )
A. B.2 C. D.4
7.(2024北京第四中学月考)在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的最大值是( )
B.
C. D.
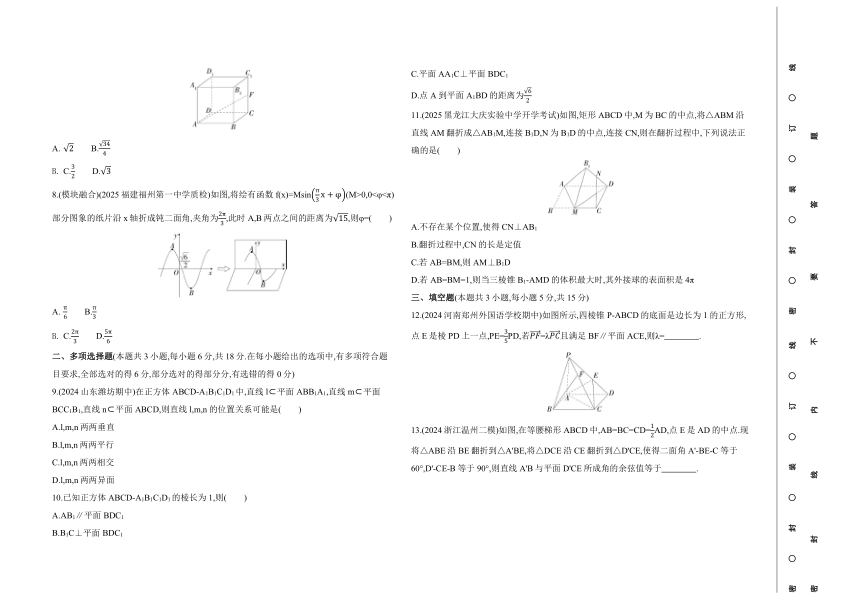
8.(模块融合)(2025福建福州第一中学质检)如图,将绘有函数f(x)=Msin(M>0,0<φ<π)部分图象的纸片沿x轴折成钝二面角,夹角为,此时A,B两点之间的距离为,则φ=( )
B.
C. D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2024山东潍坊期中)在正方体ABCD-A1B1C1D1中,直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,则直线l,m,n的位置关系可能是( )
A.l,m,n两两垂直
B.l,m,n两两平行
C.l,m,n两两相交
D.l,m,n两两异面
10.已知正方体ABCD-A1B1C1D1的棱长为1,则( )
A.AB1∥平面BDC1
B.B1C⊥平面BDC1
C.平面AA1C⊥平面BDC1
D.点A到平面A1BD的距离为
11.(2025黑龙江大庆实验中学开学考试)如图,矩形ABCD中,M为BC的中点,将△ABM沿直线AM翻折成△AB1M,连接B1D,N为B1D的中点,连接CN,则在翻折过程中,下列说法正确的是( )
A.不存在某个位置,使得CN⊥AB1
B.翻折过程中,CN的长是定值
C.若AB=BM,则AM⊥B1D
D.若AB=BM=1,则当三棱锥B1-AMD的体积最大时,其外接球的表面积是4π
三、填空题(本题共3小题,每小题5分,共15分)
12.(2024河南郑州外国语学校期中)如图所示,四棱锥P-ABCD的底面是边长为1的正方形,点E是棱PD上一点,PE=PD,若=λ且满足BF∥平面ACE,则λ= .
13.(2024浙江温州二模)如图,在等腰梯形ABCD中,AB=BC=CD=AD,点E是AD的中点.现将△ABE沿BE翻折到△A'BE,将△DCE沿CE翻折到△D'CE,使得二面角A'-BE-C等于60°,D'-CE-B等于90°,则直线A'B与平面D'CE所成角的余弦值等于 .
14.(2025湖南长沙多校联考)在棱长为2的正方体ABCD-A1B1C1D1中,P为△A1BD内一点,且AP=,则BP+C1P的最大值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)(2025黑龙江绥化一中月考)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,E,F分别为BC,PA的中点.
(1)证明:EF∥平面PDC;
(2)若AB=2AD=2,PD=1,∠ABD=30°,求点D到平面PAB的距离.
16.(15分)(2025江苏如皋中学调研)在四棱锥P-ABCD中,已知△PCD是正三角形,底面ABCD为矩形,且平面PCD⊥平面ABCD,AB=BC.
(1)证明:BC⊥平面PCD;
(2)求二面角P-BD-C的余弦值.
17.(15分)(2025江苏常州学情调研)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=4,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求直线BF和平面BCE所成角的正弦值.
18.(17分)(2025江西新余第四中学月考)如图,在三棱锥P-ABC中,AB⊥AC,AP⊥BP,CA⊥AP,BC=2,M,N分别为PB,PA的中点.
(1)证明:平面CMN与平面ABC的交线l∥平面PAB;
(2)证明:BP⊥PC;
(3)若直线CM与平面PAB的夹角为,二面角C-MN-A的正切值为,求AC的长.
19.(17分)(2024北京理工大附中月考)如图,在四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABEF沿EF折起,使BE⊥EC.
(1)若BE=3,在折起后的线段AD上是否存在一点P,使得CP∥平面ABEF 若存在,求出的值;若不存在,说明理由;
(2)求三棱锥A-CDF的体积的最大值,并求出此时点F到平面ACD的距离.
答案全解全析
1.D 若m∥α,m∥β,则α与β平行或相交,故A,C错误;
若m⊥α,α⊥β,则m∥β或m β,故B错误;
若m∥β,则必有一直线m' β且m∥m',因为m⊥α,所以m'⊥α,又m' β,所以α⊥β,故D正确.
2.C 还原正方体如图所示,
由图可知BM和ED是异面直线,故①错误;
CN和BE是平行直线,故②错误;
∵CN∥BE,∴∠EBM(或其补角)为异面直线CN与BM所成的角,为60°,故③正确;
由正方体的特征知NC⊥DM,BC⊥平面DCMN,又DM 平面DCMN,∴DM⊥BC,又NC∩BC=C,NC,BC 平面BCN,∴DM⊥平面BCN,又BN 平面BCN,∴DM⊥BN,故④正确.
3.B 因为底面ABCD为正方形,所以CD⊥AD.
因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.
又PA∩AD=A,PA,AD 平面PAD,所以CD⊥平面PAD.又CD 平面PCD,所以平面PCD⊥平面PAD,故A中结论正确.
显然平面PCD与平面PBC不垂直,故B中结论错误.
因为底面ABCD为正方形,所以BC⊥AB.
因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.
又PA∩AB=A,PA,AB 平面PAB,所以BC⊥平面PAB.又BC 平面PBC,所以平面PAB⊥平面PBC,故C中结论正确.
由BC∥AD及C中分析可知AD⊥平面PAB,又AD 平面PAD,所以平面PAB⊥平面PAD,故D中结论正确.
4.D 连接AC交BD于O,则O为BD的中点.连接PO.
由PA⊥平面ABCD,BD 平面ABCD,得PA⊥BD,
由底面ABCD是正方形,得BD⊥AC,
又PA,AC 平面PAC,PA∩AC=A,
所以BD⊥平面PAC,又PO 平面PAC,所以BD⊥PO,即点P到BD的距离为PO的长.
在Rt△PAO中,由勾股定理得PO===,故点P到直线BD的距离为.
解题技法 求点线距的常用方法
1.直接法:直接由点向直线作垂线,在三角形中利用等面积法求解.
2.间接法:如图,求P到直线l的距离,先作PO⊥α于O,再作OH⊥l于H,连接PH,可得PH⊥l,则PH的长即为P到直线l的距离.
本题中由这个结论可直接得到PO的长为点P到直线BD的距离.
5.D 选项A,如图,取CD的中点H,连接GH,FH,AG,AH,
因为A-BCDE是正四棱锥,A-CDF是正四面体,G为BE的中点,所以CD⊥GH,CD⊥AH,CD⊥FH.
因为GH∩AH=H,GH,AH 平面AGH,所以CD⊥平面AGH,
因为AH∩FH=H,AH,FH 平面AFH,所以CD⊥平面AFH,
所以平面AGH∥平面AFH,又平面AGH∩平面AFH=AH,所以平面AGH与平面AFH重合,所以A,G,H,F四点共面.
由题意知AG=HF=,GH=AF=2,所以四边形AGHF是平行四边形,所以GH∥AF,因为BC∥GH,所以BC∥AF,所以故A正确.
选项B,由A知AG∥FH,又AG 平面CDF,FH 平面CDF,所以AG∥平面CDF.
因为CD∥BE,且BE 平面CDF,CD 平面CDF,所以BE∥平面CDF,又AG 平面ABE,BE 平面ABE,且AG∩BE=G,所以平面ABE∥平面CDF,故B正确.
选项C,由A可得CD⊥平面AGHF,又FG 平面AGHF,所以FG⊥CD,故C正确.
选项D,,因为AH 平面ACD,所以FG⊥AH,
由A知四边形AGHF是平行四边形,所以四边形AGHF是菱形,与AG=,GH=2矛盾,故D错误.
6.B 如图,取B1C1的中点D,BB1的中点E,连接MD,DE,ME,则DE∥BC1,
又DE 平面ABC1,BC1 平面ABC1,所以DE∥平面ABC1,
又M为A1C1的中点,所以MD∥A1B1∥AB,
又MD 平面ABC1,AB 平面ABC1,所以MD∥平面ABC1,
又DE∩MD=D,MD,DE 平面DEM,所以平面DEM∥平面ABC1.
因为N是侧面BCC1B1内一点,且MN∥平面ABC1,平面DEM∩平面BCC1B1=DE,所以N的轨迹为线段DE,易得DE=BC1=×=2,所以点N的轨迹长度为2.
7.点拨 ①过点D1作AF的垂面,确定点P的轨迹,
→AF⊥平面D1B1E;
②等腰梯形D1GEB1中到点D1的距离最长的点为E,在Rt△D1C1E中利用勾股定理求解D1E的长度.
C 连接AC,BD,A1C1,B1D1,因为AA1⊥平面A1B1C1D1,B1D1 平面A1B1C1D1,所以AA1⊥B1D1,
又A1C1⊥B1D1,AA1∩A1C1=A1,AA1,A1C1 平面A1ACC1,所以B1D1⊥平面A1ACC1,
因为AF 平面A1ACC1,所以B1D1⊥AF,
取BC的中点E,连接B1E,C1E,D1E,BF,易得BF⊥B1E,
因为AB⊥平面B1BCC1,B1E 平面B1BCC1,所以AB⊥B1E,因为AB∩BF=B,且AB,BF 平面ABF,所以B1E⊥平面ABF,又AF 平面ABF,所以B1E⊥AF,
因为B1E∩B1D1=B1,B1D1,B1E 平面D1B1E,
所以AF⊥平面D1B1E,设平面D1B1E∩平面ABCD=GE,易得GE∥D1B1,又DB∥D1B1,所以GE∥DB,又E是BC的中点,所以G是棱CD的中点,连接GD1,
所以当点P在线段D1B1,B1E,EG,GD1(点D1除外)上时,D1P⊥AF,
在梯形D1GEB1中,D1B1=,D1G=B1E=,EG=,D1E===,
所以线段D1P长度的最大值是.
8.C 如图,过A,B分别作x轴的垂线,垂足分别为C,D,过A作y轴的垂线,过D作x轴的垂线,使其相交于点E,连接AB,BE,
则∠BDE=,BD=DE=M,
在△BDE中,由余弦定理得BE2=M2+M2-2M2cos =3M2,
由上述分析可知,x轴垂直于BD,DE,又BD∩DE=D,BD,DE 平面BDE,所以x轴⊥平面BDE,
又AE∥x轴,所以AE⊥平面BDE,
因为BE 平面BDE,所以AE⊥BE,
易,所以AE=CD=3,
在Rt△ABE中,由勾股定理得3M2+9=15,解得M=(负值舍去),
由题图知f(x)的图象过点,
所以f(0)=sin φ=,即sin φ=,
因为0<φ<π,点在递减区间内,所以φ=.
9.ACD 对于A,C,当l为BB1,m为BC,n为AB时,l,m,n两两垂直,且l,m,n两两相交,故A,C正确;
对于B,不妨设l∥m,l,m和BB1均不重合,
因为l 平面BCC1B1,m 平面BCC1B1,
所以l∥平面BCC1B1,又l 平面ABB1A1,平面ABB1A1∩平面BCC1B1=BB1,所以l∥BB1,所以m∥BB1,又BB1⊥平面ABCD,n 平面ABCD,所以BB1⊥n,所以l⊥n,m⊥n,即l,m,n不可能两两平行,故B错误;
对于D,当l为AA1,m为B1C1,n为CD时,l,m,n两两异面,故D正确.
10.AC 如图,易知AB1∥DC1,因为DC1 平面BDC1,AB1 平面BDC1,所以AB1∥平面BDC1,故A正确;
若B1C⊥平面BDC1,则B1C⊥DC1,则B1C⊥AB1,显然∠AB1C≠90°,故B错误;
因为四边形ABCD是正方形,所以BD⊥AC,又BD⊥AA1,AA1∩AC=A,AA1,AC 平面AA1C,
所以BD⊥平面AA1C,又BD 平面BDC1,所以平面AA1C⊥平面BDC1,故C正确;
设点A到平面A1BD的距离为h,
由=,得·h=S△ABD·AA1,即××××h=××1×1×1,
解得h=,故点A到平面A1BD的距离为,故D错误.
11.ABD 对于A,如图1,取AD的中点E,连接CE交MD于点F,连接ME,NE,NF,易知四边形MCDE为平行四边形,则F为DM的中点,又N为B1D的中点,所以NF∥MB1,同理得NE∥AB1.
假设CN⊥AB1,则EN⊥CN,
因为AB1⊥MB1,所以EN⊥NF,
因为NE,NF,NC共面且共点,所以不可能有EN⊥CN,EN⊥NF同时成立,即不存在某个位置,使得CN⊥AB1,A正确.
对于B,结合A的分析知∠NEC=∠B1AM,且NE=AB1,AM=EC,
在△CEN中,NC2=NE2+EC2-2NE·EC·cos∠NEC,
因为∠NEC=∠B1AM=∠BAM,所以∠NEC为定值,又NE,EC也为定值,所以NC2为定值,即翻折过程中,CN的长是定值,B正确.
对于C,如图2,取AM的中点O,连接B1O,OD,AB=BM即AB1=B1M,则AM⊥B1O.
假设AM⊥B1D,因为B1O∩B1D=B1,B1O,B1D 平面ODB1,所以AM⊥平面ODB1,
又OD 平面ODB1,所以AM⊥OD,又O为AM的中点,所以AD=MD,
因为AB=BM,M为BC的中点,所以AD=BC=2AB,且DC=CM,所以MD=CD=AB,
故AD≠MD,与AD=MD矛盾,故C错误.
对于D,因为△AMD的面积是不变的,所以只有当平面B1AM⊥平面AMD时,三棱锥B1-AMD的体积最大.
如图2,设AD的中点为H,连接OH,B1H,MH,易知AB1=B1M=1,且AB1⊥B1M,B1O⊥AM,又平面B1AM∩平面AMD=AM,平面B1AM⊥平面AMD,B1O 平面B1AM,
所以B1O⊥平面AMD,又OH 平面AMD,所以B1O⊥OH,
则AM=,B1O=AM=,OH=DM=AM=,
所以HB1==1,则HA=HD=HM=HB1=1,
所以AD的中点H即为三棱锥B1-AMD的外接球球心,且球的半径为1,故外接球的表面积是4π,D正确.
12.
解析 如图,连接BD,交AC于点O,连接OE,
由四边形ABCD是正方形,得BO=OD,
在线段PE上取点G,使得GE=ED,由PE=PD,得=,连接BG,FG,则BG∥OE,
由OE 平面ACE,BG 平面ACE,得BG∥平面ACE,
又BF∥平面ACE,BG∩BF=B,BG,BF 平面BGF,所以平面BGF∥平面ACE,
又平面PCD∩平面ACE=EC,平面PCD∩平面BGF=GF,所以GF∥EC,所以λ===.
13.
解析 设AB=2a,取CE的中点K,连接BK,A'K,易知△BCE是等边三角形,故BK⊥CE.
由题知平面BCE⊥平面D'CE,又平面BCE∩平面D'CE=CE,BK 平面BCE,BK⊥CE,
所以BK⊥平面D'CE,则直线A'B与平面D'CE所成角的余弦值等于∠A'BK的正弦值(关键点).
连接A'C,易求得BK=a,A'C=a,则cos∠A'EC==,
又cos∠A'EC==,所以A'K=a,
则cos∠A'BK==,
则sin∠A'BK==,
所以直线A'B与平面D'CE所成角的余弦值等于.
14.2
解析 如图,连接AC1与平面A1BD交于点O,连接AC,AB1,B1D1,B1C,CD1,
易知BD⊥AC,BD⊥CC1,又AC∩CC1=C且AC,CC1 平面ACC1,所以BD⊥平面ACC1,
又AC1 平面ACC1,
所以BD⊥AC1.
易知A1B⊥AB1,A1B⊥B1C1,
又AB1∩B1C1=B1且AB1,B1C1 平面AB1C1,所以A1B⊥平面AB1C1,
又AC1 平面AB1C1,
所以A1B⊥AC1,
因为BD∩A1B=B,BD,A1B 平面A1BD,所以AC1⊥平面A1BD,同理AC1⊥平面B1D1C,
且两平面将体对角线AC1三等分,
故AO=AC1=,
因为AP=,所以OP==,若P不加限制,则点P的轨迹是以A为球心,为半径的球,当P在平面A1BD上时,P在球与平面A1BD的截面圆上,故P在以O为圆心,为半径的圆上
易知△A1BD是边长为2的正三角形,其内切圆半径为,所以点P在△A1BD的内切圆上,
因为AC1⊥平面A1BD,且点C1到平面A1BD的距离为AC1=,所以C1P==,
当点P为A1D的中点时,符合题意的BP最大,为A1B=,
所以BP+C1P的最大值为2.
15.解析 (1)证法一 取PD的中点M,连接MF,CM,
因为F为PA的中点,所以MF∥AD,且MF=AD,(1分)
又E为BC的中点,所以EC=BC,又AD BC,所以EC∥AD,且EC=AD,(3分)
所以MF EC,所以四边形EFMC为平行四边形,
所以EF∥CM,(5分)
又EF 平面PDC,CM 平面PDC,
所以EF∥平面PDC.(6分)
证法二 取AD的中点G,连接FG,GE,
因为F是AP的中点,所以FG∥PD,(2分)
又FG 平面PDC,PD 平面PDC,
所以FG∥平面PDC,同理得EG∥平面PDC.(4分)
又FG∩EG=G,FG,EG 平面EFG,所以平面EFG∥平面PDC.(5分)
又EF 平面EFG,所以EF∥平面PDC.(6分)
证法三 连接AE并延长交DC的延长线于点H,连接PH,
因为E是BC的中点,且AB∥DC,
所以△AEB≌△HEC,故AE=HE,即E是AH的中点,(2分)
因为F是AP的中点,所以EF∥PH,(4分)
又H∈DC 平面PDC,EF 平面PDC,所以EF∥平面PDC.(6分)
(2)解法一 在△ABD中,AB=2AD=2,∠ABD=30°,
由正弦定理得∠ADB=90°,则BD=,(8分)
因为PD⊥平面ABCD,AD、BD 平面ABCD,
所以PD⊥AD,PD⊥BD,(9分)
在Rt△PAD中,PA==,
在Rt△PBD中,PB==2,
在等腰△PAB中,PA边上的高为=,(10分)
所以S△PAB=××=,(11分)
设点D到平面PAB的距离为d,
由VP-ABD=VD-PAB得××1××1=××d,(12分)
解得d=,即点D到平面PAB的距离为.(13分)
解法二 过点D作DM⊥AB,连接PM,过点D作DN⊥PM,交PM于点N.
因为AB⊥DM,AB⊥DP,DM,DP 平面DPM,DM∩DP=D,所以AB⊥平面DPM,(7分)
又AB 平面PAB,所以平面PAB⊥平面DPM,(8分)
又因为平面PAB∩平面DPM=PM,DN⊥PM,DN 平面DPM,
所以DN⊥平面PAB,故DN即为点D到平面PAB的距离.(9分)
因为AD2=AB2+BD2-2AB·BDcos∠ABD,
所以BD2-2BD+3=0,所以BD=.(10分)
由AD2+BD2=AB2得AD⊥BD,(11分)
在Rt△PDM中,DP=1,DM=,∠PDM=,
故PM=,所以DN==,即点D到平面PAB的距离为.(13分)
16.解析 (1)证明:因为四边形ABCD是矩形,所以BC⊥CD.(1分)
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC 平面ABCD,
所以BC⊥平面PCD.(4分)
(2)过点P作PE⊥CD,垂足为E,过点E作EF⊥BD,垂足为F,连接PF.(6分)
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PE⊥CD,PE 平面PCD,所以PE⊥平面ABCD,因为BD 平面ABCD,所以PE⊥BD.(8分)
因为BD⊥EF,PE∩EF=E,PE,EF 平面PEF,
所以BD⊥平面PEF,又PF 平面PEF,所以BD⊥PF.(10分)
所以∠PFE为二面角P-BD-C的平面角.(11分)
设AB=BC=2,
因为△PCD是正三角形,所以PE=,(12分)
因为底面ABCD为矩形,所以EF=,所以tan∠PFE==3,所以cos∠PFE=,(14分)
所以二面角P-BD-C的余弦值为.(15分)
17.解析 (1)证法一 如图,取CE的中点G,连接FG,BG.
∵F为CD的中点,∴GF∥DE且GF=DE,
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.又AB=DE,∴GF=AB,(3分)
∴四边形GFAB为平行四边形,则AF∥BG,
∵AF 平面BCE,BG 平面BCE,∴AF∥平面BCE.(5分)
证法二 取DE的中点M,连接AM,FM,
∵F为CD的中点,∴FM∥CE,因为FM 平面BCE,CE 平面BCE,∴FM∥平面BCE.(1分)
∵AB∥DE,2AB=DE,∴AB∥EM,AB=EM,
∴四边形ABEM为平行四边形,∴AM∥BE,又AM 平面BCE,BE 平面BCE,∴AM∥平面BCE.(3分)
∵AM∩FM=M,AM,FM 平面AFM,∴平面AFM∥平面BCE.(4分)
∵AF 平面AFM,∴AF∥平面BCE.(5分)
证法三 延长EB交DA的延长线于点H,连接CH,
易知AB是△DEH的中位线,所以HA=AD,(2分)
又因为F是CD的中点,所以AF∥CH,(3分)
又H∈BE 平面BCE,
所以AF∥平面BCE.(5分)
(2)证明:在(1)中证法一的基础上证明.∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.
∵DE⊥平面ACD,AF 平面ACD,∴DE⊥AF.(7分)
又CD∩DE=D,CD,DE 平面CDE,∴AF⊥平面CDE,又BG∥AF,∴BG⊥平面CDE,(9分)
∵BG 平面BCE,∴平面BCE⊥平面CDE.(10分)
(3)解法一 如图,在平面CDE内,过F作FN⊥CE于点N,连接BN,
∵平面BCE⊥平面CDE,平面BCE∩平面CDE=CE,FN 平面CDE,
∴FN⊥平面BCE,∴∠FBN为BF与平面BCE所成的角,(12分)
易得CF=CD=2,AF=ADsin 60°=4×=2,
∴FN=CFsin 45°=,BF==4,(13分)
在Rt△FNB中,sin∠FBN==,(14分)
∴直线BF和平面BCE所成角的正弦值为.(15分)
解法二 在(1)中证法一及(2)的基础下求解.设点F到平面CBE的距离为h,直线BF和平面BCE所成的角为θ.
则由线面角的定义可知sin θ=.
∵四边形ABGF为平行四边形,∴BG=AF=ADsin 60°=2.
由VF-BCE=VB-CEF,得S△BCE·h=S△CEF·BG h=.(12分)
在△CEF中,S△CEF=CF·DE=4,
在△BCE中,BE==2,CE=4,BC==2,
易知BG⊥CE,∴S△BCE=CE·BG=4,(13分)
∴h===,又BF===4,
∴sin θ==.
∴直线BF和平面BCE所成角的正弦值为.(15分)
解题技法 几何法求线面角的常用方法
1.直接法:根据线面角的定义,斜线与射影所成的角即为线面角,直接根据垂线,斜线,射影构成的直角三角形解题.
2.等体积法:对于垂线段较难找出的问题,利用等体积法可以求出垂线段的长度,设斜线与平面所成的角为θ,垂线段的长度为h,斜线段的长度为l,则sin θ=.
18.解析 (1)证明:因为M,N分别是PB,PA的中点,所以MN∥AB,(1分)
因为AB 平面ABC,MN 平面ABC,所以MN∥平面ABC,
所以MN∥l,(3分)
又MN 平面PAB,l 平面PAB,所以l∥平面PAB.(4分)
(2)证明:因为AC⊥AB,AC⊥AP,AB∩AP=A,AB,AP 平面PAB,
所以AC⊥平面PAB,(5分)
又PB 平面PAB,所以PB⊥AC,(6分)
又PB⊥AP,AC∩AP=A,AC,AP 平面PAC,所以BP⊥平面PAC,(7分)
又PC 平面PAC,所以BP⊥PC.(8分)
(3)由(2)知AC⊥平面PAB,又AC 平面ABC,所以平面ABC⊥平面PAB,连接AM(图略),
则∠AMC为直线CM与平面PAB的夹角,故∠AMC=,(9分)
设AC=a,则AB=,因为AM 平面PAB,所以AC⊥AM.故AM=AC=a,
设PA=b,则PC=,PB=,
在Rt△PAM中,由勾股定理得(4-a2-b2)+b2=a2,故b=.(11分)
把△PAB脱离出来,
过A作AG⊥MN,交MN的延长线于G,则∠CGA是二面角C-MN-A的平面角,设为θ,(13分)
所以tan θ==,则AG=a,过P作PG'∥AB,交AG的延长线于G',则AG'=2AG=a.(14分)
易知△AG'P∽△BPA,则=,即=,
故7a4-19a2+12=0,所以a=1或a=,(15分)
经检验,均符合题意.(17分)
19.解析 (1)假设存在满足条件的点P.
如图,过点P作PM∥FD,交AF于点M,连接ME,
∵CE∥FD,∴MP∥EC,∴M,P,C,E四点共面.(3分)
∵CP∥平面ABEF,CP 平面CEMP,平面ABEF∩平面CEMP=ME,
∴CP∥ME,∴四边形CEMP为平行四边形,(5分)
∴MP=CE=4-BE=1,
易得FD=6-3=3,
由MP∥FD可得==,
∴=.
故存在点P使得CP∥平面ABEF,此时=.(8分)
(2)由题意得BE⊥EF,又BE⊥EC,EC∩EF=E,EC,EF 平面CEFD,∴BE⊥平面CEFD,
又AF∥BE,∴AF⊥平面CEFD.(10分)
设BE=x(0故VA-CDF=××2×(6-x)×x=-(x-3)2+3,
∴当x=3时,VA-CDF取得最大值,最大值为3,(13分)
此时EC=1,AF=3,FD=3,DC=2,
∴AD==3,AC==,
在△ACD中,由余弦定理的推论得cos∠ADC==,∴sin∠ADC=,
∴S△ACD=DC·AD·sin∠ADC=3.(15分)
设F到平面ACD的距离为h,
由VF-ACD=VA-CDF,得S△ACD·h=3,解得h=.
故三棱锥A-CDF的体积的最大值为3,此时点F到平面ACD的距离为.(17分)
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第八单元 立体几何与空间向量(二)
满分150分,限时120分钟
考点2 空间点、直线、平面之间的位置关系
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2025江苏南通调研)若α,β为两个不同的平面,m为一条直线,则下列结论正确的是( )
A.若m∥α,m∥β,则α∥β B.若m⊥α,α⊥β,则m∥β
C.若m∥α,m∥β,则α与β相交 D.若m⊥α,m∥β,则α⊥β
2.(2024安徽模拟)下图是一个正方体的平面展开图,则在这个正方体中,
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个结论中,正确结论的序号是( )
A.①②③ B.②④
C.③④ D.①③④
3.(2024山西运城景胜中学月考)如图,PA垂直于正方形ABCD所在平面,则下列结论错误的是( )
A.平面PCD⊥平面PAD B.平面PCD⊥平面PBC
C.平面PAB⊥平面PBC D.平面PAB⊥平面PAD
4.(2025北京海淀开学考试)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的正方形,PA=,则点P到直线BD的距离为( )
A. B. C. D.
5.(2025河北衡水中学测评)如图,四棱锥A-BCDE是棱长均为2的正四棱锥,几何体A-CDF是正四面体,G为BE的中点,则下列结论错误的是( )
A.A,B,C,F四点共面 B.平面ABE∥平面CDF
C.FG⊥CD D.FG⊥平面ACD
6.(2024陕西商洛模拟预测)如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是2,M为A1C1的中点,N是侧面BCC1B1内的动点,且MN∥平面ABC1,则点N的轨迹的长度为( )
A. B.2 C. D.4
7.(2024北京第四中学月考)在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的最大值是( )
B.
C. D.
8.(模块融合)(2025福建福州第一中学质检)如图,将绘有函数f(x)=Msin(M>0,0<φ<π)部分图象的纸片沿x轴折成钝二面角,夹角为,此时A,B两点之间的距离为,则φ=( )
B.
C. D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2024山东潍坊期中)在正方体ABCD-A1B1C1D1中,直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,则直线l,m,n的位置关系可能是( )
A.l,m,n两两垂直
B.l,m,n两两平行
C.l,m,n两两相交
D.l,m,n两两异面
10.已知正方体ABCD-A1B1C1D1的棱长为1,则( )
A.AB1∥平面BDC1
B.B1C⊥平面BDC1
C.平面AA1C⊥平面BDC1
D.点A到平面A1BD的距离为
11.(2025黑龙江大庆实验中学开学考试)如图,矩形ABCD中,M为BC的中点,将△ABM沿直线AM翻折成△AB1M,连接B1D,N为B1D的中点,连接CN,则在翻折过程中,下列说法正确的是( )
A.不存在某个位置,使得CN⊥AB1
B.翻折过程中,CN的长是定值
C.若AB=BM,则AM⊥B1D
D.若AB=BM=1,则当三棱锥B1-AMD的体积最大时,其外接球的表面积是4π
三、填空题(本题共3小题,每小题5分,共15分)
12.(2024河南郑州外国语学校期中)如图所示,四棱锥P-ABCD的底面是边长为1的正方形,点E是棱PD上一点,PE=PD,若=λ且满足BF∥平面ACE,则λ= .
13.(2024浙江温州二模)如图,在等腰梯形ABCD中,AB=BC=CD=AD,点E是AD的中点.现将△ABE沿BE翻折到△A'BE,将△DCE沿CE翻折到△D'CE,使得二面角A'-BE-C等于60°,D'-CE-B等于90°,则直线A'B与平面D'CE所成角的余弦值等于 .
14.(2025湖南长沙多校联考)在棱长为2的正方体ABCD-A1B1C1D1中,P为△A1BD内一点,且AP=,则BP+C1P的最大值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)(2025黑龙江绥化一中月考)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,E,F分别为BC,PA的中点.
(1)证明:EF∥平面PDC;
(2)若AB=2AD=2,PD=1,∠ABD=30°,求点D到平面PAB的距离.
16.(15分)(2025江苏如皋中学调研)在四棱锥P-ABCD中,已知△PCD是正三角形,底面ABCD为矩形,且平面PCD⊥平面ABCD,AB=BC.
(1)证明:BC⊥平面PCD;
(2)求二面角P-BD-C的余弦值.
17.(15分)(2025江苏常州学情调研)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=4,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求直线BF和平面BCE所成角的正弦值.
18.(17分)(2025江西新余第四中学月考)如图,在三棱锥P-ABC中,AB⊥AC,AP⊥BP,CA⊥AP,BC=2,M,N分别为PB,PA的中点.
(1)证明:平面CMN与平面ABC的交线l∥平面PAB;
(2)证明:BP⊥PC;
(3)若直线CM与平面PAB的夹角为,二面角C-MN-A的正切值为,求AC的长.
19.(17分)(2024北京理工大附中月考)如图,在四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABEF沿EF折起,使BE⊥EC.
(1)若BE=3,在折起后的线段AD上是否存在一点P,使得CP∥平面ABEF 若存在,求出的值;若不存在,说明理由;
(2)求三棱锥A-CDF的体积的最大值,并求出此时点F到平面ACD的距离.
答案全解全析
1.D 若m∥α,m∥β,则α与β平行或相交,故A,C错误;
若m⊥α,α⊥β,则m∥β或m β,故B错误;
若m∥β,则必有一直线m' β且m∥m',因为m⊥α,所以m'⊥α,又m' β,所以α⊥β,故D正确.
2.C 还原正方体如图所示,
由图可知BM和ED是异面直线,故①错误;
CN和BE是平行直线,故②错误;
∵CN∥BE,∴∠EBM(或其补角)为异面直线CN与BM所成的角,为60°,故③正确;
由正方体的特征知NC⊥DM,BC⊥平面DCMN,又DM 平面DCMN,∴DM⊥BC,又NC∩BC=C,NC,BC 平面BCN,∴DM⊥平面BCN,又BN 平面BCN,∴DM⊥BN,故④正确.
3.B 因为底面ABCD为正方形,所以CD⊥AD.
因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.
又PA∩AD=A,PA,AD 平面PAD,所以CD⊥平面PAD.又CD 平面PCD,所以平面PCD⊥平面PAD,故A中结论正确.
显然平面PCD与平面PBC不垂直,故B中结论错误.
因为底面ABCD为正方形,所以BC⊥AB.
因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.
又PA∩AB=A,PA,AB 平面PAB,所以BC⊥平面PAB.又BC 平面PBC,所以平面PAB⊥平面PBC,故C中结论正确.
由BC∥AD及C中分析可知AD⊥平面PAB,又AD 平面PAD,所以平面PAB⊥平面PAD,故D中结论正确.
4.D 连接AC交BD于O,则O为BD的中点.连接PO.
由PA⊥平面ABCD,BD 平面ABCD,得PA⊥BD,
由底面ABCD是正方形,得BD⊥AC,
又PA,AC 平面PAC,PA∩AC=A,
所以BD⊥平面PAC,又PO 平面PAC,所以BD⊥PO,即点P到BD的距离为PO的长.
在Rt△PAO中,由勾股定理得PO===,故点P到直线BD的距离为.
解题技法 求点线距的常用方法
1.直接法:直接由点向直线作垂线,在三角形中利用等面积法求解.
2.间接法:如图,求P到直线l的距离,先作PO⊥α于O,再作OH⊥l于H,连接PH,可得PH⊥l,则PH的长即为P到直线l的距离.
本题中由这个结论可直接得到PO的长为点P到直线BD的距离.
5.D 选项A,如图,取CD的中点H,连接GH,FH,AG,AH,
因为A-BCDE是正四棱锥,A-CDF是正四面体,G为BE的中点,所以CD⊥GH,CD⊥AH,CD⊥FH.
因为GH∩AH=H,GH,AH 平面AGH,所以CD⊥平面AGH,
因为AH∩FH=H,AH,FH 平面AFH,所以CD⊥平面AFH,
所以平面AGH∥平面AFH,又平面AGH∩平面AFH=AH,所以平面AGH与平面AFH重合,所以A,G,H,F四点共面.
由题意知AG=HF=,GH=AF=2,所以四边形AGHF是平行四边形,所以GH∥AF,因为BC∥GH,所以BC∥AF,所以故A正确.
选项B,由A知AG∥FH,又AG 平面CDF,FH 平面CDF,所以AG∥平面CDF.
因为CD∥BE,且BE 平面CDF,CD 平面CDF,所以BE∥平面CDF,又AG 平面ABE,BE 平面ABE,且AG∩BE=G,所以平面ABE∥平面CDF,故B正确.
选项C,由A可得CD⊥平面AGHF,又FG 平面AGHF,所以FG⊥CD,故C正确.
选项D,,因为AH 平面ACD,所以FG⊥AH,
由A知四边形AGHF是平行四边形,所以四边形AGHF是菱形,与AG=,GH=2矛盾,故D错误.
6.B 如图,取B1C1的中点D,BB1的中点E,连接MD,DE,ME,则DE∥BC1,
又DE 平面ABC1,BC1 平面ABC1,所以DE∥平面ABC1,
又M为A1C1的中点,所以MD∥A1B1∥AB,
又MD 平面ABC1,AB 平面ABC1,所以MD∥平面ABC1,
又DE∩MD=D,MD,DE 平面DEM,所以平面DEM∥平面ABC1.
因为N是侧面BCC1B1内一点,且MN∥平面ABC1,平面DEM∩平面BCC1B1=DE,所以N的轨迹为线段DE,易得DE=BC1=×=2,所以点N的轨迹长度为2.
7.点拨 ①过点D1作AF的垂面,确定点P的轨迹,
→AF⊥平面D1B1E;
②等腰梯形D1GEB1中到点D1的距离最长的点为E,在Rt△D1C1E中利用勾股定理求解D1E的长度.
C 连接AC,BD,A1C1,B1D1,因为AA1⊥平面A1B1C1D1,B1D1 平面A1B1C1D1,所以AA1⊥B1D1,
又A1C1⊥B1D1,AA1∩A1C1=A1,AA1,A1C1 平面A1ACC1,所以B1D1⊥平面A1ACC1,
因为AF 平面A1ACC1,所以B1D1⊥AF,
取BC的中点E,连接B1E,C1E,D1E,BF,易得BF⊥B1E,
因为AB⊥平面B1BCC1,B1E 平面B1BCC1,所以AB⊥B1E,因为AB∩BF=B,且AB,BF 平面ABF,所以B1E⊥平面ABF,又AF 平面ABF,所以B1E⊥AF,
因为B1E∩B1D1=B1,B1D1,B1E 平面D1B1E,
所以AF⊥平面D1B1E,设平面D1B1E∩平面ABCD=GE,易得GE∥D1B1,又DB∥D1B1,所以GE∥DB,又E是BC的中点,所以G是棱CD的中点,连接GD1,
所以当点P在线段D1B1,B1E,EG,GD1(点D1除外)上时,D1P⊥AF,
在梯形D1GEB1中,D1B1=,D1G=B1E=,EG=,D1E===,
所以线段D1P长度的最大值是.
8.C 如图,过A,B分别作x轴的垂线,垂足分别为C,D,过A作y轴的垂线,过D作x轴的垂线,使其相交于点E,连接AB,BE,
则∠BDE=,BD=DE=M,
在△BDE中,由余弦定理得BE2=M2+M2-2M2cos =3M2,
由上述分析可知,x轴垂直于BD,DE,又BD∩DE=D,BD,DE 平面BDE,所以x轴⊥平面BDE,
又AE∥x轴,所以AE⊥平面BDE,
因为BE 平面BDE,所以AE⊥BE,
易,所以AE=CD=3,
在Rt△ABE中,由勾股定理得3M2+9=15,解得M=(负值舍去),
由题图知f(x)的图象过点,
所以f(0)=sin φ=,即sin φ=,
因为0<φ<π,点在递减区间内,所以φ=.
9.ACD 对于A,C,当l为BB1,m为BC,n为AB时,l,m,n两两垂直,且l,m,n两两相交,故A,C正确;
对于B,不妨设l∥m,l,m和BB1均不重合,
因为l 平面BCC1B1,m 平面BCC1B1,
所以l∥平面BCC1B1,又l 平面ABB1A1,平面ABB1A1∩平面BCC1B1=BB1,所以l∥BB1,所以m∥BB1,又BB1⊥平面ABCD,n 平面ABCD,所以BB1⊥n,所以l⊥n,m⊥n,即l,m,n不可能两两平行,故B错误;
对于D,当l为AA1,m为B1C1,n为CD时,l,m,n两两异面,故D正确.
10.AC 如图,易知AB1∥DC1,因为DC1 平面BDC1,AB1 平面BDC1,所以AB1∥平面BDC1,故A正确;
若B1C⊥平面BDC1,则B1C⊥DC1,则B1C⊥AB1,显然∠AB1C≠90°,故B错误;
因为四边形ABCD是正方形,所以BD⊥AC,又BD⊥AA1,AA1∩AC=A,AA1,AC 平面AA1C,
所以BD⊥平面AA1C,又BD 平面BDC1,所以平面AA1C⊥平面BDC1,故C正确;
设点A到平面A1BD的距离为h,
由=,得·h=S△ABD·AA1,即××××h=××1×1×1,
解得h=,故点A到平面A1BD的距离为,故D错误.
11.ABD 对于A,如图1,取AD的中点E,连接CE交MD于点F,连接ME,NE,NF,易知四边形MCDE为平行四边形,则F为DM的中点,又N为B1D的中点,所以NF∥MB1,同理得NE∥AB1.
假设CN⊥AB1,则EN⊥CN,
因为AB1⊥MB1,所以EN⊥NF,
因为NE,NF,NC共面且共点,所以不可能有EN⊥CN,EN⊥NF同时成立,即不存在某个位置,使得CN⊥AB1,A正确.
对于B,结合A的分析知∠NEC=∠B1AM,且NE=AB1,AM=EC,
在△CEN中,NC2=NE2+EC2-2NE·EC·cos∠NEC,
因为∠NEC=∠B1AM=∠BAM,所以∠NEC为定值,又NE,EC也为定值,所以NC2为定值,即翻折过程中,CN的长是定值,B正确.
对于C,如图2,取AM的中点O,连接B1O,OD,AB=BM即AB1=B1M,则AM⊥B1O.
假设AM⊥B1D,因为B1O∩B1D=B1,B1O,B1D 平面ODB1,所以AM⊥平面ODB1,
又OD 平面ODB1,所以AM⊥OD,又O为AM的中点,所以AD=MD,
因为AB=BM,M为BC的中点,所以AD=BC=2AB,且DC=CM,所以MD=CD=AB,
故AD≠MD,与AD=MD矛盾,故C错误.
对于D,因为△AMD的面积是不变的,所以只有当平面B1AM⊥平面AMD时,三棱锥B1-AMD的体积最大.
如图2,设AD的中点为H,连接OH,B1H,MH,易知AB1=B1M=1,且AB1⊥B1M,B1O⊥AM,又平面B1AM∩平面AMD=AM,平面B1AM⊥平面AMD,B1O 平面B1AM,
所以B1O⊥平面AMD,又OH 平面AMD,所以B1O⊥OH,
则AM=,B1O=AM=,OH=DM=AM=,
所以HB1==1,则HA=HD=HM=HB1=1,
所以AD的中点H即为三棱锥B1-AMD的外接球球心,且球的半径为1,故外接球的表面积是4π,D正确.
12.
解析 如图,连接BD,交AC于点O,连接OE,
由四边形ABCD是正方形,得BO=OD,
在线段PE上取点G,使得GE=ED,由PE=PD,得=,连接BG,FG,则BG∥OE,
由OE 平面ACE,BG 平面ACE,得BG∥平面ACE,
又BF∥平面ACE,BG∩BF=B,BG,BF 平面BGF,所以平面BGF∥平面ACE,
又平面PCD∩平面ACE=EC,平面PCD∩平面BGF=GF,所以GF∥EC,所以λ===.
13.
解析 设AB=2a,取CE的中点K,连接BK,A'K,易知△BCE是等边三角形,故BK⊥CE.
由题知平面BCE⊥平面D'CE,又平面BCE∩平面D'CE=CE,BK 平面BCE,BK⊥CE,
所以BK⊥平面D'CE,则直线A'B与平面D'CE所成角的余弦值等于∠A'BK的正弦值(关键点).
连接A'C,易求得BK=a,A'C=a,则cos∠A'EC==,
又cos∠A'EC==,所以A'K=a,
则cos∠A'BK==,
则sin∠A'BK==,
所以直线A'B与平面D'CE所成角的余弦值等于.
14.2
解析 如图,连接AC1与平面A1BD交于点O,连接AC,AB1,B1D1,B1C,CD1,
易知BD⊥AC,BD⊥CC1,又AC∩CC1=C且AC,CC1 平面ACC1,所以BD⊥平面ACC1,
又AC1 平面ACC1,
所以BD⊥AC1.
易知A1B⊥AB1,A1B⊥B1C1,
又AB1∩B1C1=B1且AB1,B1C1 平面AB1C1,所以A1B⊥平面AB1C1,
又AC1 平面AB1C1,
所以A1B⊥AC1,
因为BD∩A1B=B,BD,A1B 平面A1BD,所以AC1⊥平面A1BD,同理AC1⊥平面B1D1C,
且两平面将体对角线AC1三等分,
故AO=AC1=,
因为AP=,所以OP==,若P不加限制,则点P的轨迹是以A为球心,为半径的球,当P在平面A1BD上时,P在球与平面A1BD的截面圆上,故P在以O为圆心,为半径的圆上
易知△A1BD是边长为2的正三角形,其内切圆半径为,所以点P在△A1BD的内切圆上,
因为AC1⊥平面A1BD,且点C1到平面A1BD的距离为AC1=,所以C1P==,
当点P为A1D的中点时,符合题意的BP最大,为A1B=,
所以BP+C1P的最大值为2.
15.解析 (1)证法一 取PD的中点M,连接MF,CM,
因为F为PA的中点,所以MF∥AD,且MF=AD,(1分)
又E为BC的中点,所以EC=BC,又AD BC,所以EC∥AD,且EC=AD,(3分)
所以MF EC,所以四边形EFMC为平行四边形,
所以EF∥CM,(5分)
又EF 平面PDC,CM 平面PDC,
所以EF∥平面PDC.(6分)
证法二 取AD的中点G,连接FG,GE,
因为F是AP的中点,所以FG∥PD,(2分)
又FG 平面PDC,PD 平面PDC,
所以FG∥平面PDC,同理得EG∥平面PDC.(4分)
又FG∩EG=G,FG,EG 平面EFG,所以平面EFG∥平面PDC.(5分)
又EF 平面EFG,所以EF∥平面PDC.(6分)
证法三 连接AE并延长交DC的延长线于点H,连接PH,
因为E是BC的中点,且AB∥DC,
所以△AEB≌△HEC,故AE=HE,即E是AH的中点,(2分)
因为F是AP的中点,所以EF∥PH,(4分)
又H∈DC 平面PDC,EF 平面PDC,所以EF∥平面PDC.(6分)
(2)解法一 在△ABD中,AB=2AD=2,∠ABD=30°,
由正弦定理得∠ADB=90°,则BD=,(8分)
因为PD⊥平面ABCD,AD、BD 平面ABCD,
所以PD⊥AD,PD⊥BD,(9分)
在Rt△PAD中,PA==,
在Rt△PBD中,PB==2,
在等腰△PAB中,PA边上的高为=,(10分)
所以S△PAB=××=,(11分)
设点D到平面PAB的距离为d,
由VP-ABD=VD-PAB得××1××1=××d,(12分)
解得d=,即点D到平面PAB的距离为.(13分)
解法二 过点D作DM⊥AB,连接PM,过点D作DN⊥PM,交PM于点N.
因为AB⊥DM,AB⊥DP,DM,DP 平面DPM,DM∩DP=D,所以AB⊥平面DPM,(7分)
又AB 平面PAB,所以平面PAB⊥平面DPM,(8分)
又因为平面PAB∩平面DPM=PM,DN⊥PM,DN 平面DPM,
所以DN⊥平面PAB,故DN即为点D到平面PAB的距离.(9分)
因为AD2=AB2+BD2-2AB·BDcos∠ABD,
所以BD2-2BD+3=0,所以BD=.(10分)
由AD2+BD2=AB2得AD⊥BD,(11分)
在Rt△PDM中,DP=1,DM=,∠PDM=,
故PM=,所以DN==,即点D到平面PAB的距离为.(13分)
16.解析 (1)证明:因为四边形ABCD是矩形,所以BC⊥CD.(1分)
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC 平面ABCD,
所以BC⊥平面PCD.(4分)
(2)过点P作PE⊥CD,垂足为E,过点E作EF⊥BD,垂足为F,连接PF.(6分)
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PE⊥CD,PE 平面PCD,所以PE⊥平面ABCD,因为BD 平面ABCD,所以PE⊥BD.(8分)
因为BD⊥EF,PE∩EF=E,PE,EF 平面PEF,
所以BD⊥平面PEF,又PF 平面PEF,所以BD⊥PF.(10分)
所以∠PFE为二面角P-BD-C的平面角.(11分)
设AB=BC=2,
因为△PCD是正三角形,所以PE=,(12分)
因为底面ABCD为矩形,所以EF=,所以tan∠PFE==3,所以cos∠PFE=,(14分)
所以二面角P-BD-C的余弦值为.(15分)
17.解析 (1)证法一 如图,取CE的中点G,连接FG,BG.
∵F为CD的中点,∴GF∥DE且GF=DE,
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.又AB=DE,∴GF=AB,(3分)
∴四边形GFAB为平行四边形,则AF∥BG,
∵AF 平面BCE,BG 平面BCE,∴AF∥平面BCE.(5分)
证法二 取DE的中点M,连接AM,FM,
∵F为CD的中点,∴FM∥CE,因为FM 平面BCE,CE 平面BCE,∴FM∥平面BCE.(1分)
∵AB∥DE,2AB=DE,∴AB∥EM,AB=EM,
∴四边形ABEM为平行四边形,∴AM∥BE,又AM 平面BCE,BE 平面BCE,∴AM∥平面BCE.(3分)
∵AM∩FM=M,AM,FM 平面AFM,∴平面AFM∥平面BCE.(4分)
∵AF 平面AFM,∴AF∥平面BCE.(5分)
证法三 延长EB交DA的延长线于点H,连接CH,
易知AB是△DEH的中位线,所以HA=AD,(2分)
又因为F是CD的中点,所以AF∥CH,(3分)
又H∈BE 平面BCE,
所以AF∥平面BCE.(5分)
(2)证明:在(1)中证法一的基础上证明.∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.
∵DE⊥平面ACD,AF 平面ACD,∴DE⊥AF.(7分)
又CD∩DE=D,CD,DE 平面CDE,∴AF⊥平面CDE,又BG∥AF,∴BG⊥平面CDE,(9分)
∵BG 平面BCE,∴平面BCE⊥平面CDE.(10分)
(3)解法一 如图,在平面CDE内,过F作FN⊥CE于点N,连接BN,
∵平面BCE⊥平面CDE,平面BCE∩平面CDE=CE,FN 平面CDE,
∴FN⊥平面BCE,∴∠FBN为BF与平面BCE所成的角,(12分)
易得CF=CD=2,AF=ADsin 60°=4×=2,
∴FN=CFsin 45°=,BF==4,(13分)
在Rt△FNB中,sin∠FBN==,(14分)
∴直线BF和平面BCE所成角的正弦值为.(15分)
解法二 在(1)中证法一及(2)的基础下求解.设点F到平面CBE的距离为h,直线BF和平面BCE所成的角为θ.
则由线面角的定义可知sin θ=.
∵四边形ABGF为平行四边形,∴BG=AF=ADsin 60°=2.
由VF-BCE=VB-CEF,得S△BCE·h=S△CEF·BG h=.(12分)
在△CEF中,S△CEF=CF·DE=4,
在△BCE中,BE==2,CE=4,BC==2,
易知BG⊥CE,∴S△BCE=CE·BG=4,(13分)
∴h===,又BF===4,
∴sin θ==.
∴直线BF和平面BCE所成角的正弦值为.(15分)
解题技法 几何法求线面角的常用方法
1.直接法:根据线面角的定义,斜线与射影所成的角即为线面角,直接根据垂线,斜线,射影构成的直角三角形解题.
2.等体积法:对于垂线段较难找出的问题,利用等体积法可以求出垂线段的长度,设斜线与平面所成的角为θ,垂线段的长度为h,斜线段的长度为l,则sin θ=.
18.解析 (1)证明:因为M,N分别是PB,PA的中点,所以MN∥AB,(1分)
因为AB 平面ABC,MN 平面ABC,所以MN∥平面ABC,
所以MN∥l,(3分)
又MN 平面PAB,l 平面PAB,所以l∥平面PAB.(4分)
(2)证明:因为AC⊥AB,AC⊥AP,AB∩AP=A,AB,AP 平面PAB,
所以AC⊥平面PAB,(5分)
又PB 平面PAB,所以PB⊥AC,(6分)
又PB⊥AP,AC∩AP=A,AC,AP 平面PAC,所以BP⊥平面PAC,(7分)
又PC 平面PAC,所以BP⊥PC.(8分)
(3)由(2)知AC⊥平面PAB,又AC 平面ABC,所以平面ABC⊥平面PAB,连接AM(图略),
则∠AMC为直线CM与平面PAB的夹角,故∠AMC=,(9分)
设AC=a,则AB=,因为AM 平面PAB,所以AC⊥AM.故AM=AC=a,
设PA=b,则PC=,PB=,
在Rt△PAM中,由勾股定理得(4-a2-b2)+b2=a2,故b=.(11分)
把△PAB脱离出来,
过A作AG⊥MN,交MN的延长线于G,则∠CGA是二面角C-MN-A的平面角,设为θ,(13分)
所以tan θ==,则AG=a,过P作PG'∥AB,交AG的延长线于G',则AG'=2AG=a.(14分)
易知△AG'P∽△BPA,则=,即=,
故7a4-19a2+12=0,所以a=1或a=,(15分)
经检验,均符合题意.(17分)
19.解析 (1)假设存在满足条件的点P.
如图,过点P作PM∥FD,交AF于点M,连接ME,
∵CE∥FD,∴MP∥EC,∴M,P,C,E四点共面.(3分)
∵CP∥平面ABEF,CP 平面CEMP,平面ABEF∩平面CEMP=ME,
∴CP∥ME,∴四边形CEMP为平行四边形,(5分)
∴MP=CE=4-BE=1,
易得FD=6-3=3,
由MP∥FD可得==,
∴=.
故存在点P使得CP∥平面ABEF,此时=.(8分)
(2)由题意得BE⊥EF,又BE⊥EC,EC∩EF=E,EC,EF 平面CEFD,∴BE⊥平面CEFD,
又AF∥BE,∴AF⊥平面CEFD.(10分)
设BE=x(0
∴当x=3时,VA-CDF取得最大值,最大值为3,(13分)
此时EC=1,AF=3,FD=3,DC=2,
∴AD==3,AC==,
在△ACD中,由余弦定理的推论得cos∠ADC==,∴sin∠ADC=,
∴S△ACD=DC·AD·sin∠ADC=3.(15分)
设F到平面ACD的距离为h,
由VF-ACD=VA-CDF,得S△ACD·h=3,解得h=.
故三棱锥A-CDF的体积的最大值为3,此时点F到平面ACD的距离为.(17分)
同课章节目录
