第十二单元 概率与统计(三)(含解析)-《巅峰突破》2026版高中数学高三一轮复习
文档属性
| 名称 | 第十二单元 概率与统计(三)(含解析)-《巅峰突破》2026版高中数学高三一轮复习 |  | |
| 格式 | docx | ||
| 文件大小 | 156.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 11:23:59 | ||
图片预览



文档简介
(
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第十二单元 概率与统计(三)
满分120分,限时100分钟
考点5 随机抽样、常用统计图表、用样本估计总体 考点6 回归分析 考点7 独立性检验
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024四川乐山调研)对四组数据进行统计,获得散点图,关于其样本相关系数的比较正确的是( )
A.r2C.r22.(2025湖南名校联考联合体联考)某学校的高一、高二、高三年级分别有学生1 000人、1 200人、800人,用分层随机抽样的方法从全体学生中抽取一个容量为30的样本,抽出的高一、高二、高三年级学生的平均身高分别为165 cm,168 cm,171 cm,则估计该校学生的平均身高是( )
A.166.4 cm B.167.2 cm C.167.8 cm D.170.0 cm
3.(2025四川绵阳诊断)某公司根据近几年的经营结果,得到广告支出与获得的利润的数据如下:
广告支出x/万元 2 5 8 11 15 19
利润y/万元 33 45 50 53 58 64
根据表中数据可得,利润y关于广告支出x的经验回归方程为=1.65x+.据此经验回归方程估计,当利润达到100万元时,广告支出为( )
A.30万元 B.32万元 C.36万元 D.40万元
4.(2024广东广州荔湾联考)从某小区抽取100户居民进行月用电量调查,发现他们的月用电量(单位:kW·h)都在[50,350]内,进行适当分组(最后一组为闭区间,其余每组为左闭右开的区间)后,画出频率分布直方图如图所示.
则在被调查的用户中,月用电量(单位:kW·h)的第71百分位数为( )
A.205 B.215 C.225 D.235
5.(2025河北十县联考)某企业五个部门2024年第三季度的营业收入占比和净利润占比统计如下表所示:
第一部门 第二部门 第三部门 第四部门 第五部门
营业收 入占比 48.4% 15.8% 18.2% 10.8% 6.8%
净利润 占比 62.8% -3.3% 15.5% 20.2% 4.8%
若该企业本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),则( )
A.各部门营业收入占比的极差为41.6
B.各部门营业收入占比的第75百分位数为10.8%
C.第二部门本季度的营业利润为正
D.第三部门本季度的营业利润率大约为27.68%
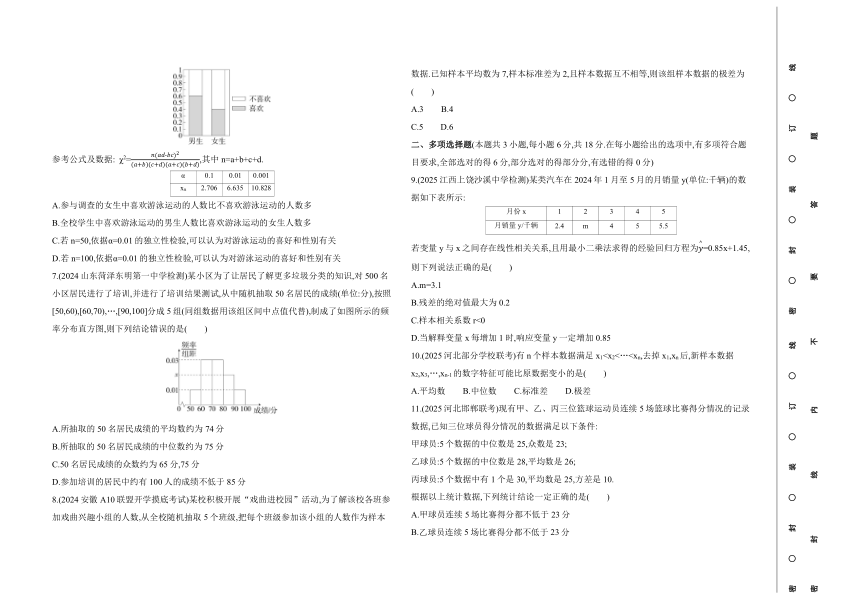
6.(2025重庆涪陵第五中学校开学考试)某学校开设了游泳选修课,教练为了解学生对游泳运动的喜好和性别是否有关,在全校学生中选取了男、女生各n人进行调查,并绘制出了如下图所示的等高堆积条形图,则( )
参考公式及数据: χ2=,其中n=a+b+c+d.
α 0.1 0.01 0.001
xα 2.706 6.635 10.828
A.参与调查的女生中喜欢游泳运动的人数比不喜欢游泳运动的人数多
B.全校学生中喜欢游泳运动的男生人数比喜欢游泳运动的女生人数多
C.若n=50,依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关
D.若n=100,依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关
7.(2024山东菏泽东明第一中学检测)某小区为了让居民了解更多垃圾分类的知识,对500名小区居民进行了培训,并进行了培训结果测试,从中随机抽取50名居民的成绩(单位:分),按照[50,60),[60,70),…,[90,100]分成5组(同组数据用该组区间中点值代替),制成了如图所示的频率分布直方图,则下列结论错误的是( )
A.所抽取的50名居民成绩的平均数约为74分
B.所抽取的50名居民成绩的中位数约为75分
C.50名居民成绩的众数约为65分,75分
D.参加培训的居民中约有100人的成绩不低于85分
8.(2024安徽A10联盟开学摸底考试)某校积极开展“戏曲进校园”活动,为了解该校各班参加戏曲兴趣小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本标准差为2,且样本数据互不相等,则该组样本数据的极差为( )
A.3 B.4
C.5 D.6
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2025江西上饶沙溪中学检测)某类汽车在2024年1月至5月的月销量y(单位:千辆)的数据如下表所示:
月份x 1 2 3 4 5
月销量y/千辆 2.4 m 4 5 5.5
若变量y与x之间存在线性相关关系,且用最小二乘法求得的经验回归方程为=0.85x+1.45,则下列说法正确的是( )
A.m=3.1
B.残差的绝对值最大为0.2
C.样本相关系数r<0
D.当解释变量x每增加1时,响应变量y一定增加0.85
10.(2025河北部分学校联考)有n个样本数据满足x1A.平均数 B.中位数 C.标准差 D.极差
11.(2025河北邯郸联考)现有甲、乙、丙三位篮球运动员连续5场篮球比赛得分情况的记录数据,已知三位球员得分情况的数据满足以下条件:
甲球员:5个数据的中位数是25,众数是23;
乙球员:5个数据的中位数是28,平均数是26;
丙球员:5个数据中有1个是30,平均数是25,方差是10.
根据以上统计数据,下列统计结论一定正确的是( )
A.甲球员连续5场比赛得分都不低于23分
B.乙球员连续5场比赛得分都不低于23分
C.丙球员连续5场比赛得分都不低于23分
D.丙球员连续5场比赛得分的第60百分位数大于23分
三、填空题(本题共3小题,每小题5分,共15分)
12.(2025湖南名校联考联合体联考)某公司针对“社交电商用户是否存在性别差异”进行调查,共调查了40n(n∈N*)个人,得到列联表:
是社交电商用户 不是社交电商用户 合计
男性 8n 12n 20n
女性 12n 8n 20n
合计 20n 20n 40n
已知x0.05=3.841,若根据α=0.05的独立性检验认为“社交电商用户存在性别差异”,则n的最小值为 .
13.(2025浙南名校联盟联考)已知某中学的3个年级各有学生300人,300人,400人,现采用分层随机抽样的方法从3个年级的学生中抽取10人,对他们的体重进行了统计.若3个年级被抽到的学生体重的平均值分别为48 kg,52 kg,55 kg,方差分别为4,10,1.将这10名学生的体重W(kg)作为样本,则样本的方差为 .
14.(2025黑龙江哈尔滨第九中学校阶段检测)若一组样本数据x1,x2,…,xn的平均数为10,另一组样本数据2x1+4,2x2+4,…,2xn+4的方差为8,则两组样本数据合并为一组样本数据后的方差是 .
四、解答题(本题共3小题,共47分.解答应写出文字说明、证明过程或演算步骤)
15.(15分)某景区的各景点从2014年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是2015—2024年(对应年份代码1~10)该景区的旅游人数y(单位:万)与年份x的数据:
年份代码x 1 2 3 4 5 6 7 8 9 10
旅游人数 y/万 300 283 321 345 372 435 486 527 622 800
该景区为了预测2027年的旅游人数,建立了y与x的两个回归模型:
模型①:由最小二乘法求得y与x的经验回归方程为=50.8x+169.7;
模型②:由散点图中样本点的分布,可以认为样本点集中在曲线y=aebx的附近.
(1)根据表中数据,求模型②的回归方程=;(的值精确到个位,的值精确到0.001)
(2)根据下表中的数据,比较两种模型的决定系数R2,并选择拟合精度更高、更可靠的模型,预测2027年该景区的旅游人数(单位:万,精确到个位).
回归方程 ①=50.8x+169.7 ②=
(yi-)2 30 407 14 607
参考公式:在经验回归方程=x+中,=,=-,R2=1-.
参考数据:e5.46≈235,e1.40≈4.06.
5.5 449 6.05 83
(xi-)(yi-) (xi-)(ui-)
4 195 9
表中ui=ln yi,=ui.
16.(15分)(2025浙江杭州第二中学期中)某公司招聘销售员,提供了两种日工资结算方案,方案一:每日底薪100元,每销售一单提成2元;方案二:每日底薪200元,销售的前50单没有提成,从第51单开始,每完成一单提成4元.该公司记录了销售员的每日人均业务量,现随机抽取一个季度的数据,将样本数据分为[25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘销售员做出日工资方案的选择,并说明理由(同组中的数据用该组区间的中点值代替);
(3)已知公司现有销售员400人,某销售员希望自己的业务量在公司所有销售员中处于前40名,那么他每日的平均业务量至少应达到多少单
17.(17分)(2025吉林长春质量监测)某医学研究团队经过研究初步得出检测是否患某种疾病和某项医学指标有关,利用该指标制订一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性(患病),小于或等于c的人判定为阴性(未患病).此检测标准的漏诊率是将患病者判定为阴性的概率,误诊率是将未患病者判定为阳性的概率.
(1)随机抽取男女各500人进行检测,采用临界值c=97.5进行判定时,误判共10人(漏诊与误诊之和),其中2男8女,写出2×2列联表,依据小概率值α=0.050的独立性检验,能否认为误判与性别有关
(2)经过大量调查,得到如下的患病者和未患病者该指标的频率分布表:
指标 [95, 100] (100, 105] (105, 110] (110, 115] (115, 120] (120, 125] (125, 130]
患病者 频率 0.01 0.06 0.17 0.18 0.2 0.2 0.18
指标 [70, 75] (75, 80] (80, 85] (85, 90] (90, 95] (95, 100] (100, 105]
未患病 者频率 0.19 0.2 0.2 0.18 0.17 0.05 0.01
假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.若漏诊率和误诊率同时控制在2.5%以内(小于或等于2.5%),求临界值c的范围;
(3)在(2)的条件下,求出误判率(漏诊率与误诊率之和)最小时的临界值c0及c0对应的误诊率和漏诊率.
附: χ2=,n=a+b+c+d.
α 0.100 0.050 0.010 0.001
xα 2.706 3.841 6.635 10.828
答案全解全析
强基精测卷3
1.A 由题中的散点图可以看出,图1和图3是正相关,则样本相关系数大于0,即r1>0,r3>0;图2和图4是负相关,则样本相关系数小于0,即r2<0,r4<0.又图1和图2中的点相对于图3和图4中的点更加集中,所以r1更接近1,r2更接近-1,所以r22.C 由题意得,在高一、高二、高三年级的学生中抽取的人数分别为×30=12,×30=8,
所以估计该校学生的平均身高是×(10×165+12×168+8×171)=167.8(cm).
3.D 由题表中数据得==10,=,解得=34,所以=1.65x+34.
令=100,即1.65x+34=100,解得x=40.
故估计当利润达到100万元时,广告支出为40万元.
4.C 由题图得(0.002 4+0.003 6+0.006+x+0.002 4+0.001 2)×区间[50,200)对应的频率为(0.002 4+0.003 6+0.006)×50=0.6,区间[50,250)对应的频率为(0.002 4+0.003 6+0.006+0.004 4)×50=0.82,所以这组数据的第71百分位数在[200,250)内.
设这组数据的第71百分位数为a,则=,解得a=225,即在被调查的用户中,月用电量(单位:kW·h)的第71百分位数为225.
解题技法 由频率分布直方图求百分位数的方法
(1)要注意频率分布直方图中各小长方形的面积就是数据落在相应各组内的频率;
(2)求解时先估计百分位数在哪一组内,然后设出百分位数,再利用方程思想求解.
5.D 对于A,各部门营业为48.4%-6.8%=41.6%,故A错误;
对于B,将各部门营业收入占比按从小到大的顺序排列,为6.8%、10.8%、15.8%、18.2%、48.4%,因为5×0.75=3.75,所以各部门营业收入占比的为18.2%,故B错误;
对于C,第二部门本季度的营业利润率为32.5%×<0,所以第二部门本季度的营业利润为负,故C错误;
对于D,第三部门本季度的营业利润率为32.5%×≈27.68%,故D正确.
解题技法
计算n个数据的第p百分位数的步骤
(1)按从小到大的顺序排列原始数据.
(2)计算i=n×p%.
(3)若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
6.D 由题中等高堆积条形图可知,参与调查的女生中喜欢游泳运动的人数比不喜欢游泳运动的人数少,故A错误.
因为全校学生中男生和女生的人数比不确定,所以不能确定全校学生中喜欢游泳运动的男生人数比喜欢游泳运动的女生人数多,故B错误.
结合题中等高堆积条形图可得如下2×2列联表:
单位:人
性别 游泳 合计
喜欢 不喜欢
男生 0.6n 0.4n n
女生 0.4n 0.6n n
合计 n n 2n
易得χ2==0.08n.
当n=50时, χ2=0.08n=4<6.635=x0.01,所以依据α=0.01的独立性检验,不可以认为对游泳运动的喜好和性别有关,故C错误.
当n=100时, χ2=0.08n=8>6.635=x0.01,所以依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关,故D正确.
7.B 由题图得0.1+0.3+0.3+10x+0.1=1,解得x=0.02,55×0.1+65×0.3+75×0.3+85×0.2+95×0.1=74(分),故A中结论正确.
因为0.1+0.3=0.4<0.5,0.1+0.3+0.3=0.7>0.5,所以则0.1+0.3+(x-70)×0.03=0.5,解得x=,故B中结论错误.
由题图得,从左向右看,最高矩形为第2个和第3个,所以75分,故C中结论正确.
由题图得,成绩不低于85分的频率为0.2×0.5+0.1=0.2,所以参加培训的居民中,成绩不低于85分的人数约为0.2×500=100,故D中结论正确.
8.D 不妨设5个班级的样本数据分别为a,b,c,d,e(a即a+b+c+d+e=35,且(a-7)2+(b-7)2+(c-7)2+(d-7)2+(e-7)2=20.
易知e≥d+1≥c+2≥b+3≥a+4,所以a+b+c+d+e≤5e-10,所以e≥9.
因为五个数据减7的平方数为整数,所以a-7,b-7,c-7,d-7,e-7的绝对值均不超过4.
当e=11时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=4,因为a,b,c,d均为整数且均不相同,所以e=11不符合题意.
当e=10时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=11,因为a,b,c,d均为整数且均不相同,所以四个平方数只能为0,1,1,9,所以a=4,b=6,c=7,d=8,此时极差为6.
当e=9时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=16,因为a,b,c,d均为整数且均不相同,所以e=9不符合题意.
综上,该组样本数据的极差为6.
9.AB 由题表得==3,==,将其代入=0.85x+1.45,得=0.85×3+1.45,解得m=3.1,故A正确;
1月至5月各月的(0.85×1+1.45)=0.1,3.1-(0.85×2+1.45)=-0.05,4-(0.85×3+1.45)=0,5-(0.85×4+1.45)=0.15,5.5-(0.85×5+1.45)=-0.2,所以残差的绝对值最大为0.2,故B正确;
由题表知,y与x呈正相关,则r>0,故C错误;
当解释变量x每增加1时,响应变量y不一定增加0.85,故D错误.
10.ACD 不妨设样本数据为1,2,8,10,则其平均数为=5.25.
去掉1和10后,新数据的平均数为=5,所以平均数可能变小,故A符合.
当n为偶数时,比如n=4,此时原数据和新数据的中位数均为,中位数不变;
当n为奇数时,比如n=5,此时原数据和新数据的中位数均为x3,中位数不变,故B不符合.
去掉x1,xn后,数据的波动性变小,所以标准差变小,故C符合.
易得原数据的极差为xn-x1,新数据的极差为xn-1-x2,又x111.AD 设甲球员的5场篮球比赛得分数据按从小到大排列为x1,x2,x3,x4,x5,则x3=25,且23至少出现2次,所以x1=x2=23,故A中结论一定正确.
设乙球员的5场篮球比赛得分数据按从小到大排列为y1,y2,y3,y4,y5,则y3=28.
取y1=20,y2=22,y4=30,y5=30,满足平均数为26,但有2场比赛得分低于23分,故B中结论不一定正确.
设丙球员的5场篮球比赛得分数据按从小到大排列为z1,z2,z3,z4,z5,
由题意得[++++]=10,
所以++++==50,
不妨令z5=30,则=25.
因为z1,z2,z3,z4,z5的平均数为25,所以z1+z2+z3+z4=95.
取z1=20,z2=25,z3=25,z4=25,满足以上条件,但有1场比赛得分低于23分,故C中结论不一定正确.
结合C中分析,若z1=30,则z2,z3,z4,z5>30,所以>50,与题意不符;
同理可得z2=30,z3=30,z4=30时均不合题意,所以z5=30,所以z1+z2+z3+z4=95.
因为5×60%=3,所以丙球员连续5场比赛得分数据的第60百分位数为.
若≤23,则≤23,所以z1+z2+z3+z4≤92,与z1+z2+z3+z4=95矛盾,
所以>23,即丙球员连续5场比赛得分的第60百分位数大于23分,故D中结论一定正确.
12.3
解析 易得χ2==n,由已知可得n≥x0.05=3.841,所以n≥3.841×=2.400 625,
又n∈N*,所以n的最小值为3.
13.13
解析 易得3个年级抽取的学生人数分别为3,3,4,
所以=×(3×48+3×52+4×55)=52(kg),
所以样本的方差为×[4+(48-52)2]+×[10+(52-52)2]+×[1+(55-52)2]=13.
解题技法
在分层随机抽样中,如果分为2层,第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n,第1层和第2层样本的平均数分别为,,方差分别为,,则总样本的平均数=+=+,总样本的方差s2=[+]+[+]=[+]+[+].
14.54
解析 因为数据x1,x2,…,xn的平均数为10,
所以数据2x1+4,2x2+4,…,2xn+4的平均数为2×10+4=24,
所以数据2x1+4,2x2+4,…,2xn+4的方差为·==-×n×102=-400=8,所以=102n.
将两组数据合并后,新数据的平均数为×(10n+24n)=17,
所以新数据的方差为+=(5-86xi+458n)=(5×102n-86×10n+458n)=54.
解题技法
(1)若数据x1,x2,…,xn的平均数为,则mx1+a,mx2+a,…,mxn+a的平均数是m+a.
(2)若数据x1,x2,…,xn的方差为s2,则
①数据x1+a,x2+a,…,xn+a的方差也是s2;
②数据ax1,ax2,…,axn的方差是a2s2.
15.解析 (1)对y=aebx两边分别取自然对数,得ln y=bx+ln a.(1分)
令u=ln y,c=ln a,得u=bx+c.(2分)
易得==≈0.108,=-=6.05-0.108×5.5=5.456,(4分)
所以=≈e5.46≈235,(5分)
所以ln =0.108x+ln 235,
所以模型②的回归方程为=235e0.108x.(7分)
(2)因为30 407>14 607,所以>,
所以1-<1-,即<,(10分)
所以回归模型②的拟合效果更好.(12分)
2027年即x=13,此时=235e0.108×13≈235e1.40≈235×4.06≈954(万),故预测2027年该景区的旅游人数为954万.(15分)
解题技法 常见的非线性经验回归方程的转换
曲线方程 变换公式 变换后的线性函数
y=axb c=ln a, v=ln x, u=ln y u=c+bv
y=aebx c=ln a, u=ln y u=c+bx
y=a c=ln a, v=, u=ln y u=c+bv
y=a+bln x v=ln x y=a+bv
16.解析 (1)由题图得(0.005×3+2a+0.03+0.015)×10=1,解得a=0.02.(2分)
(2)由题图得,每日人均业务量的平均值为(30×0.005+40×0.005+50×0.02+60×0.03+70×0.02+80×0.015+90×0.005)×10=62(单).(4分)
方案一的人均日收入为100+62×2=224(元).(6分)
方案二的人均日收入为200+(62-50)×4=248(元).(8分)
因为248元>224元,所以选择方案二.(9分)
(3)40÷400=0.1,所以该销售员的业务量应超过90%的公司销售人员.(11分)
由题图得,前5组的频率和为(0.005×2+0.02+0.03+0.02)×10=0.8,
前6组的频率和为(0.005×2+0.02+0.03+0.02+0.015)×10=0.95.
设该销售员每日的平均业务量为x单,则(x-75)×0.015+0.8>0.9,解得x>81.7.(13分)
又x∈N*,所以x的最小正整数值为82.
故他每日的平均业务量至少应达到82单.(15分)
17.解析 (1)2×2列联表如下:
误判人数 未误判人数 总计
男性 2 498 500
女性 8 492 500
总计 10 990 1 000
(3分)
χ2=≈3.636<3.841=x0.050,(5分)
所以依据小概率值α=0.050的独立性检验,不能认为误判与性别有关.(6分)
(2)因为漏诊率小于或等于2.5%,所以由题中频率分布表可知,c∈(100,105],
所以c≤100+×5=101.25.(8分)
因为误诊率小于或等于2.5%,所以由题中频率分布表可知,c∈(95,100],
所以c≥100-×5=98.5.(10分)
综上,临界值c的取值范围为[98.5,101.25].(12分)
(3)由(2)得c∈[98.5,101.25],故c0=98.5,(13分)
所以误诊率为0.01+×0.05=0.025,即2.5%;(15分)
漏诊率为×0.01=0.007,即0.7%.(17分)
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第十二单元 概率与统计(三)
满分120分,限时100分钟
考点5 随机抽样、常用统计图表、用样本估计总体 考点6 回归分析 考点7 独立性检验
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024四川乐山调研)对四组数据进行统计,获得散点图,关于其样本相关系数的比较正确的是( )
A.r2
A.166.4 cm B.167.2 cm C.167.8 cm D.170.0 cm
3.(2025四川绵阳诊断)某公司根据近几年的经营结果,得到广告支出与获得的利润的数据如下:
广告支出x/万元 2 5 8 11 15 19
利润y/万元 33 45 50 53 58 64
根据表中数据可得,利润y关于广告支出x的经验回归方程为=1.65x+.据此经验回归方程估计,当利润达到100万元时,广告支出为( )
A.30万元 B.32万元 C.36万元 D.40万元
4.(2024广东广州荔湾联考)从某小区抽取100户居民进行月用电量调查,发现他们的月用电量(单位:kW·h)都在[50,350]内,进行适当分组(最后一组为闭区间,其余每组为左闭右开的区间)后,画出频率分布直方图如图所示.
则在被调查的用户中,月用电量(单位:kW·h)的第71百分位数为( )
A.205 B.215 C.225 D.235
5.(2025河北十县联考)某企业五个部门2024年第三季度的营业收入占比和净利润占比统计如下表所示:
第一部门 第二部门 第三部门 第四部门 第五部门
营业收 入占比 48.4% 15.8% 18.2% 10.8% 6.8%
净利润 占比 62.8% -3.3% 15.5% 20.2% 4.8%
若该企业本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),则( )
A.各部门营业收入占比的极差为41.6
B.各部门营业收入占比的第75百分位数为10.8%
C.第二部门本季度的营业利润为正
D.第三部门本季度的营业利润率大约为27.68%
6.(2025重庆涪陵第五中学校开学考试)某学校开设了游泳选修课,教练为了解学生对游泳运动的喜好和性别是否有关,在全校学生中选取了男、女生各n人进行调查,并绘制出了如下图所示的等高堆积条形图,则( )
参考公式及数据: χ2=,其中n=a+b+c+d.
α 0.1 0.01 0.001
xα 2.706 6.635 10.828
A.参与调查的女生中喜欢游泳运动的人数比不喜欢游泳运动的人数多
B.全校学生中喜欢游泳运动的男生人数比喜欢游泳运动的女生人数多
C.若n=50,依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关
D.若n=100,依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关
7.(2024山东菏泽东明第一中学检测)某小区为了让居民了解更多垃圾分类的知识,对500名小区居民进行了培训,并进行了培训结果测试,从中随机抽取50名居民的成绩(单位:分),按照[50,60),[60,70),…,[90,100]分成5组(同组数据用该组区间中点值代替),制成了如图所示的频率分布直方图,则下列结论错误的是( )
A.所抽取的50名居民成绩的平均数约为74分
B.所抽取的50名居民成绩的中位数约为75分
C.50名居民成绩的众数约为65分,75分
D.参加培训的居民中约有100人的成绩不低于85分
8.(2024安徽A10联盟开学摸底考试)某校积极开展“戏曲进校园”活动,为了解该校各班参加戏曲兴趣小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本标准差为2,且样本数据互不相等,则该组样本数据的极差为( )
A.3 B.4
C.5 D.6
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2025江西上饶沙溪中学检测)某类汽车在2024年1月至5月的月销量y(单位:千辆)的数据如下表所示:
月份x 1 2 3 4 5
月销量y/千辆 2.4 m 4 5 5.5
若变量y与x之间存在线性相关关系,且用最小二乘法求得的经验回归方程为=0.85x+1.45,则下列说法正确的是( )
A.m=3.1
B.残差的绝对值最大为0.2
C.样本相关系数r<0
D.当解释变量x每增加1时,响应变量y一定增加0.85
10.(2025河北部分学校联考)有n个样本数据满足x1
11.(2025河北邯郸联考)现有甲、乙、丙三位篮球运动员连续5场篮球比赛得分情况的记录数据,已知三位球员得分情况的数据满足以下条件:
甲球员:5个数据的中位数是25,众数是23;
乙球员:5个数据的中位数是28,平均数是26;
丙球员:5个数据中有1个是30,平均数是25,方差是10.
根据以上统计数据,下列统计结论一定正确的是( )
A.甲球员连续5场比赛得分都不低于23分
B.乙球员连续5场比赛得分都不低于23分
C.丙球员连续5场比赛得分都不低于23分
D.丙球员连续5场比赛得分的第60百分位数大于23分
三、填空题(本题共3小题,每小题5分,共15分)
12.(2025湖南名校联考联合体联考)某公司针对“社交电商用户是否存在性别差异”进行调查,共调查了40n(n∈N*)个人,得到列联表:
是社交电商用户 不是社交电商用户 合计
男性 8n 12n 20n
女性 12n 8n 20n
合计 20n 20n 40n
已知x0.05=3.841,若根据α=0.05的独立性检验认为“社交电商用户存在性别差异”,则n的最小值为 .
13.(2025浙南名校联盟联考)已知某中学的3个年级各有学生300人,300人,400人,现采用分层随机抽样的方法从3个年级的学生中抽取10人,对他们的体重进行了统计.若3个年级被抽到的学生体重的平均值分别为48 kg,52 kg,55 kg,方差分别为4,10,1.将这10名学生的体重W(kg)作为样本,则样本的方差为 .
14.(2025黑龙江哈尔滨第九中学校阶段检测)若一组样本数据x1,x2,…,xn的平均数为10,另一组样本数据2x1+4,2x2+4,…,2xn+4的方差为8,则两组样本数据合并为一组样本数据后的方差是 .
四、解答题(本题共3小题,共47分.解答应写出文字说明、证明过程或演算步骤)
15.(15分)某景区的各景点从2014年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是2015—2024年(对应年份代码1~10)该景区的旅游人数y(单位:万)与年份x的数据:
年份代码x 1 2 3 4 5 6 7 8 9 10
旅游人数 y/万 300 283 321 345 372 435 486 527 622 800
该景区为了预测2027年的旅游人数,建立了y与x的两个回归模型:
模型①:由最小二乘法求得y与x的经验回归方程为=50.8x+169.7;
模型②:由散点图中样本点的分布,可以认为样本点集中在曲线y=aebx的附近.
(1)根据表中数据,求模型②的回归方程=;(的值精确到个位,的值精确到0.001)
(2)根据下表中的数据,比较两种模型的决定系数R2,并选择拟合精度更高、更可靠的模型,预测2027年该景区的旅游人数(单位:万,精确到个位).
回归方程 ①=50.8x+169.7 ②=
(yi-)2 30 407 14 607
参考公式:在经验回归方程=x+中,=,=-,R2=1-.
参考数据:e5.46≈235,e1.40≈4.06.
5.5 449 6.05 83
(xi-)(yi-) (xi-)(ui-)
4 195 9
表中ui=ln yi,=ui.
16.(15分)(2025浙江杭州第二中学期中)某公司招聘销售员,提供了两种日工资结算方案,方案一:每日底薪100元,每销售一单提成2元;方案二:每日底薪200元,销售的前50单没有提成,从第51单开始,每完成一单提成4元.该公司记录了销售员的每日人均业务量,现随机抽取一个季度的数据,将样本数据分为[25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘销售员做出日工资方案的选择,并说明理由(同组中的数据用该组区间的中点值代替);
(3)已知公司现有销售员400人,某销售员希望自己的业务量在公司所有销售员中处于前40名,那么他每日的平均业务量至少应达到多少单
17.(17分)(2025吉林长春质量监测)某医学研究团队经过研究初步得出检测是否患某种疾病和某项医学指标有关,利用该指标制订一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性(患病),小于或等于c的人判定为阴性(未患病).此检测标准的漏诊率是将患病者判定为阴性的概率,误诊率是将未患病者判定为阳性的概率.
(1)随机抽取男女各500人进行检测,采用临界值c=97.5进行判定时,误判共10人(漏诊与误诊之和),其中2男8女,写出2×2列联表,依据小概率值α=0.050的独立性检验,能否认为误判与性别有关
(2)经过大量调查,得到如下的患病者和未患病者该指标的频率分布表:
指标 [95, 100] (100, 105] (105, 110] (110, 115] (115, 120] (120, 125] (125, 130]
患病者 频率 0.01 0.06 0.17 0.18 0.2 0.2 0.18
指标 [70, 75] (75, 80] (80, 85] (85, 90] (90, 95] (95, 100] (100, 105]
未患病 者频率 0.19 0.2 0.2 0.18 0.17 0.05 0.01
假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.若漏诊率和误诊率同时控制在2.5%以内(小于或等于2.5%),求临界值c的范围;
(3)在(2)的条件下,求出误判率(漏诊率与误诊率之和)最小时的临界值c0及c0对应的误诊率和漏诊率.
附: χ2=,n=a+b+c+d.
α 0.100 0.050 0.010 0.001
xα 2.706 3.841 6.635 10.828
答案全解全析
强基精测卷3
1.A 由题中的散点图可以看出,图1和图3是正相关,则样本相关系数大于0,即r1>0,r3>0;图2和图4是负相关,则样本相关系数小于0,即r2<0,r4<0.又图1和图2中的点相对于图3和图4中的点更加集中,所以r1更接近1,r2更接近-1,所以r2
所以估计该校学生的平均身高是×(10×165+12×168+8×171)=167.8(cm).
3.D 由题表中数据得==10,=,解得=34,所以=1.65x+34.
令=100,即1.65x+34=100,解得x=40.
故估计当利润达到100万元时,广告支出为40万元.
4.C 由题图得(0.002 4+0.003 6+0.006+x+0.002 4+0.001 2)×区间[50,200)对应的频率为(0.002 4+0.003 6+0.006)×50=0.6,区间[50,250)对应的频率为(0.002 4+0.003 6+0.006+0.004 4)×50=0.82,所以这组数据的第71百分位数在[200,250)内.
设这组数据的第71百分位数为a,则=,解得a=225,即在被调查的用户中,月用电量(单位:kW·h)的第71百分位数为225.
解题技法 由频率分布直方图求百分位数的方法
(1)要注意频率分布直方图中各小长方形的面积就是数据落在相应各组内的频率;
(2)求解时先估计百分位数在哪一组内,然后设出百分位数,再利用方程思想求解.
5.D 对于A,各部门营业为48.4%-6.8%=41.6%,故A错误;
对于B,将各部门营业收入占比按从小到大的顺序排列,为6.8%、10.8%、15.8%、18.2%、48.4%,因为5×0.75=3.75,所以各部门营业收入占比的为18.2%,故B错误;
对于C,第二部门本季度的营业利润率为32.5%×<0,所以第二部门本季度的营业利润为负,故C错误;
对于D,第三部门本季度的营业利润率为32.5%×≈27.68%,故D正确.
解题技法
计算n个数据的第p百分位数的步骤
(1)按从小到大的顺序排列原始数据.
(2)计算i=n×p%.
(3)若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
6.D 由题中等高堆积条形图可知,参与调查的女生中喜欢游泳运动的人数比不喜欢游泳运动的人数少,故A错误.
因为全校学生中男生和女生的人数比不确定,所以不能确定全校学生中喜欢游泳运动的男生人数比喜欢游泳运动的女生人数多,故B错误.
结合题中等高堆积条形图可得如下2×2列联表:
单位:人
性别 游泳 合计
喜欢 不喜欢
男生 0.6n 0.4n n
女生 0.4n 0.6n n
合计 n n 2n
易得χ2==0.08n.
当n=50时, χ2=0.08n=4<6.635=x0.01,所以依据α=0.01的独立性检验,不可以认为对游泳运动的喜好和性别有关,故C错误.
当n=100时, χ2=0.08n=8>6.635=x0.01,所以依据α=0.01的独立性检验,可以认为对游泳运动的喜好和性别有关,故D正确.
7.B 由题图得0.1+0.3+0.3+10x+0.1=1,解得x=0.02,55×0.1+65×0.3+75×0.3+85×0.2+95×0.1=74(分),故A中结论正确.
因为0.1+0.3=0.4<0.5,0.1+0.3+0.3=0.7>0.5,所以则0.1+0.3+(x-70)×0.03=0.5,解得x=,故B中结论错误.
由题图得,从左向右看,最高矩形为第2个和第3个,所以75分,故C中结论正确.
由题图得,成绩不低于85分的频率为0.2×0.5+0.1=0.2,所以参加培训的居民中,成绩不低于85分的人数约为0.2×500=100,故D中结论正确.
8.D 不妨设5个班级的样本数据分别为a,b,c,d,e(a
易知e≥d+1≥c+2≥b+3≥a+4,所以a+b+c+d+e≤5e-10,所以e≥9.
因为五个数据减7的平方数为整数,所以a-7,b-7,c-7,d-7,e-7的绝对值均不超过4.
当e=11时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=4,因为a,b,c,d均为整数且均不相同,所以e=11不符合题意.
当e=10时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=11,因为a,b,c,d均为整数且均不相同,所以四个平方数只能为0,1,1,9,所以a=4,b=6,c=7,d=8,此时极差为6.
当e=9时,(a-7)2+(b-7)2+(c-7)2+(d-7)2=16,因为a,b,c,d均为整数且均不相同,所以e=9不符合题意.
综上,该组样本数据的极差为6.
9.AB 由题表得==3,==,将其代入=0.85x+1.45,得=0.85×3+1.45,解得m=3.1,故A正确;
1月至5月各月的(0.85×1+1.45)=0.1,3.1-(0.85×2+1.45)=-0.05,4-(0.85×3+1.45)=0,5-(0.85×4+1.45)=0.15,5.5-(0.85×5+1.45)=-0.2,所以残差的绝对值最大为0.2,故B正确;
由题表知,y与x呈正相关,则r>0,故C错误;
当解释变量x每增加1时,响应变量y不一定增加0.85,故D错误.
10.ACD 不妨设样本数据为1,2,8,10,则其平均数为=5.25.
去掉1和10后,新数据的平均数为=5,所以平均数可能变小,故A符合.
当n为偶数时,比如n=4,此时原数据和新数据的中位数均为,中位数不变;
当n为奇数时,比如n=5,此时原数据和新数据的中位数均为x3,中位数不变,故B不符合.
去掉x1,xn后,数据的波动性变小,所以标准差变小,故C符合.
易得原数据的极差为xn-x1,新数据的极差为xn-1-x2,又x1
设乙球员的5场篮球比赛得分数据按从小到大排列为y1,y2,y3,y4,y5,则y3=28.
取y1=20,y2=22,y4=30,y5=30,满足平均数为26,但有2场比赛得分低于23分,故B中结论不一定正确.
设丙球员的5场篮球比赛得分数据按从小到大排列为z1,z2,z3,z4,z5,
由题意得[++++]=10,
所以++++==50,
不妨令z5=30,则=25.
因为z1,z2,z3,z4,z5的平均数为25,所以z1+z2+z3+z4=95.
取z1=20,z2=25,z3=25,z4=25,满足以上条件,但有1场比赛得分低于23分,故C中结论不一定正确.
结合C中分析,若z1=30,则z2,z3,z4,z5>30,所以>50,与题意不符;
同理可得z2=30,z3=30,z4=30时均不合题意,所以z5=30,所以z1+z2+z3+z4=95.
因为5×60%=3,所以丙球员连续5场比赛得分数据的第60百分位数为.
若≤23,则≤23,所以z1+z2+z3+z4≤92,与z1+z2+z3+z4=95矛盾,
所以>23,即丙球员连续5场比赛得分的第60百分位数大于23分,故D中结论一定正确.
12.3
解析 易得χ2==n,由已知可得n≥x0.05=3.841,所以n≥3.841×=2.400 625,
又n∈N*,所以n的最小值为3.
13.13
解析 易得3个年级抽取的学生人数分别为3,3,4,
所以=×(3×48+3×52+4×55)=52(kg),
所以样本的方差为×[4+(48-52)2]+×[10+(52-52)2]+×[1+(55-52)2]=13.
解题技法
在分层随机抽样中,如果分为2层,第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n,第1层和第2层样本的平均数分别为,,方差分别为,,则总样本的平均数=+=+,总样本的方差s2=[+]+[+]=[+]+[+].
14.54
解析 因为数据x1,x2,…,xn的平均数为10,
所以数据2x1+4,2x2+4,…,2xn+4的平均数为2×10+4=24,
所以数据2x1+4,2x2+4,…,2xn+4的方差为·==-×n×102=-400=8,所以=102n.
将两组数据合并后,新数据的平均数为×(10n+24n)=17,
所以新数据的方差为+=(5-86xi+458n)=(5×102n-86×10n+458n)=54.
解题技法
(1)若数据x1,x2,…,xn的平均数为,则mx1+a,mx2+a,…,mxn+a的平均数是m+a.
(2)若数据x1,x2,…,xn的方差为s2,则
①数据x1+a,x2+a,…,xn+a的方差也是s2;
②数据ax1,ax2,…,axn的方差是a2s2.
15.解析 (1)对y=aebx两边分别取自然对数,得ln y=bx+ln a.(1分)
令u=ln y,c=ln a,得u=bx+c.(2分)
易得==≈0.108,=-=6.05-0.108×5.5=5.456,(4分)
所以=≈e5.46≈235,(5分)
所以ln =0.108x+ln 235,
所以模型②的回归方程为=235e0.108x.(7分)
(2)因为30 407>14 607,所以>,
所以1-<1-,即<,(10分)
所以回归模型②的拟合效果更好.(12分)
2027年即x=13,此时=235e0.108×13≈235e1.40≈235×4.06≈954(万),故预测2027年该景区的旅游人数为954万.(15分)
解题技法 常见的非线性经验回归方程的转换
曲线方程 变换公式 变换后的线性函数
y=axb c=ln a, v=ln x, u=ln y u=c+bv
y=aebx c=ln a, u=ln y u=c+bx
y=a c=ln a, v=, u=ln y u=c+bv
y=a+bln x v=ln x y=a+bv
16.解析 (1)由题图得(0.005×3+2a+0.03+0.015)×10=1,解得a=0.02.(2分)
(2)由题图得,每日人均业务量的平均值为(30×0.005+40×0.005+50×0.02+60×0.03+70×0.02+80×0.015+90×0.005)×10=62(单).(4分)
方案一的人均日收入为100+62×2=224(元).(6分)
方案二的人均日收入为200+(62-50)×4=248(元).(8分)
因为248元>224元,所以选择方案二.(9分)
(3)40÷400=0.1,所以该销售员的业务量应超过90%的公司销售人员.(11分)
由题图得,前5组的频率和为(0.005×2+0.02+0.03+0.02)×10=0.8,
前6组的频率和为(0.005×2+0.02+0.03+0.02+0.015)×10=0.95.
设该销售员每日的平均业务量为x单,则(x-75)×0.015+0.8>0.9,解得x>81.7.(13分)
又x∈N*,所以x的最小正整数值为82.
故他每日的平均业务量至少应达到82单.(15分)
17.解析 (1)2×2列联表如下:
误判人数 未误判人数 总计
男性 2 498 500
女性 8 492 500
总计 10 990 1 000
(3分)
χ2=≈3.636<3.841=x0.050,(5分)
所以依据小概率值α=0.050的独立性检验,不能认为误判与性别有关.(6分)
(2)因为漏诊率小于或等于2.5%,所以由题中频率分布表可知,c∈(100,105],
所以c≤100+×5=101.25.(8分)
因为误诊率小于或等于2.5%,所以由题中频率分布表可知,c∈(95,100],
所以c≥100-×5=98.5.(10分)
综上,临界值c的取值范围为[98.5,101.25].(12分)
(3)由(2)得c∈[98.5,101.25],故c0=98.5,(13分)
所以误诊率为0.01+×0.05=0.025,即2.5%;(15分)
漏诊率为×0.01=0.007,即0.7%.(17分)
同课章节目录
