2026年高三数学上学期专题训练:数列(含解析)
文档属性
| 名称 | 2026年高三数学上学期专题训练:数列(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 17:53:00 | ||
图片预览



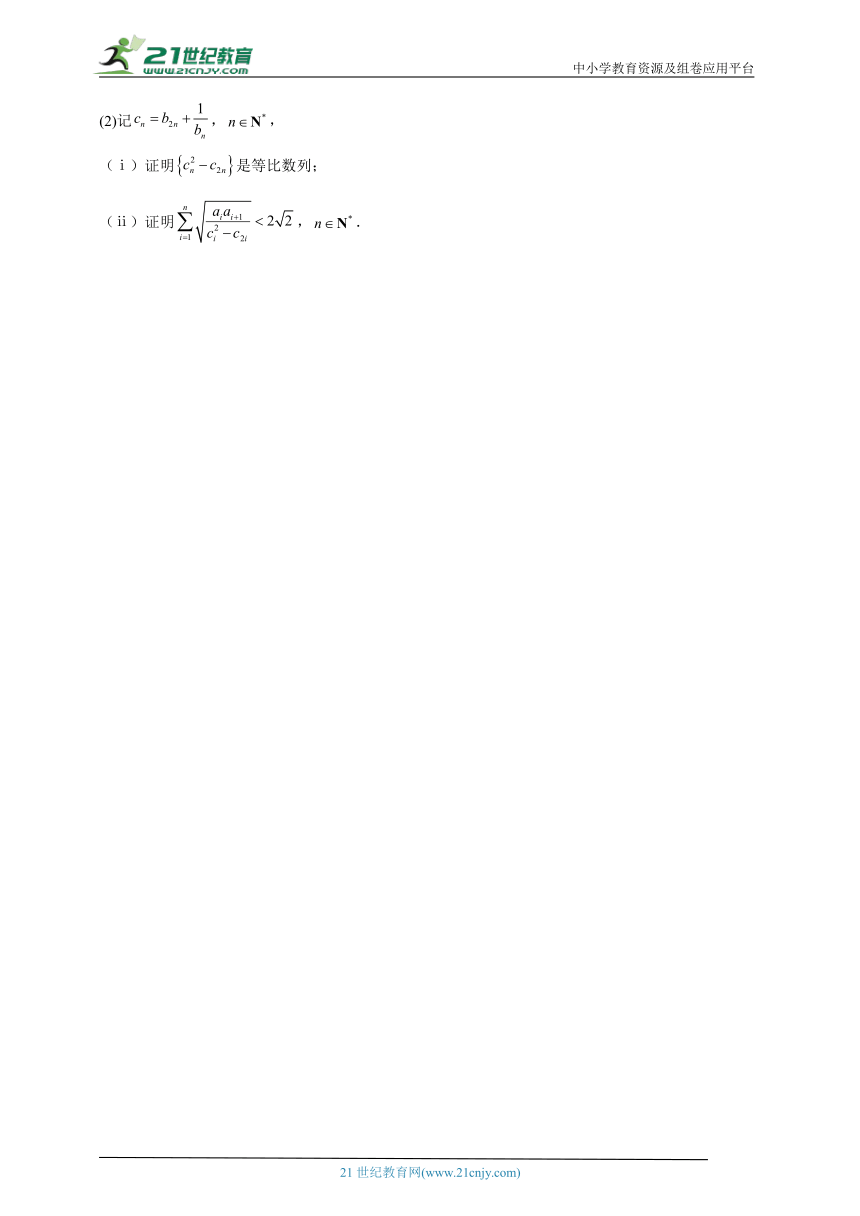

文档简介
中小学教育资源及组卷应用平台
2026年高三数学上学期专题训练:数列
一、单选题
1.(2025·江西新余·模拟预测)下列说法正确的是( )
A.已知,则且
B.命题“”是真命题
C.是的充分条件,则
D.若等比数列的通项公式为,则其前项和
2.(2025·江西新余·模拟预测)已知数列满足,且,则数列的通项公式为( )
A. B.
C. D.
3.(2025·四川广安·模拟预测)已知数列满足,,则使得成立的最小自然数为( )
A.5 B.6 C.7 D.8
4.(2025·四川成都·一模)记为等比数列的前项和,若,则的公比为( )
A.2 B. C. D.
5.(2025·江苏连云港·模拟预测)已知等比数列的前项和为,且,则( )
A. B. C. D.
6.(2025·云南丽江·模拟预测)已知等比数列的各项均为正数,且,则( )
A.2014 B.2024 C.2025 D.2026
7.(2025·广东惠州·模拟预测)已知等差数列的首项,公差,在中每相邻两项之间都插入3个数,组成一个新的等差数列,则( )
A. B.
C. D.
8.(2025·四川绵阳·模拟预测)已知数列满足,,,则下列选项正确的是( )
A. B. C. D.是递增数列
二、多选题
9.(2025·海南三亚·一模)数列为等差数列,为其前项和,已知,则( )
A. B.
C. D.当或时,最大
10.(2025·河南许昌·模拟预测)已知数列满足,,则下列说法正确的是( )
A.为中的最小项
B.对任意的,,都有
C.存在,使得,,成等差数列
D.对任意的,,都有
11.(2025·广西河池·二模)已知数列满足且,则下列说法正确的是( )
A.
B.数列是周期数列
C.是等差数列
D.数列的通项公式为
三、填空题
12.(2025·云南临沧·模拟预测)已知数列中,,,,则数列的通项公式为 .
13.(2025·四川绵阳·模拟预测)已知数列中,,,则数列的前n项和的最大值等于
14.(2025·河北邢台·二模)已知数列的前n项和为,且,,则 .
四、解答题
15.(2025·江西·模拟预测)已知数列的首项.
(1)求数列的通项公式;
(2)若恒成立,求实数的取值范围.
16.(2024·河北·模拟预测)记为各项均为正数的数列的前项和,已知.
(1)求数列的通项公式;
(2)若数列满足,求数列的前项和.
17.(2025·四川成都·一模)记为数列的前项和,已知,且.
(1)求,,;
(2)在下列两个结论中,任选一个加以证明;(若两个都证明,以首选计分)
①是等比数列;②是等比数列.
(3)记为数列的前项和,求.
18.(2025·江苏连云港·模拟预测)在数列中,,对于,,,成等差数列,其公差为.
(1)判断是否成等比数列?并说明理由;
(2)证明:,,成等比数列;
(3)设,数列的前项和为,证明:.
19.(2025·湖南长沙·三模)已知等差数列的第2项为3,其前5项和为25.数列是公比大于0的等比数列,,.
(1)求和的通项公式;
(2)记,,
(ⅰ)证明是等比数列;
(ⅱ)证明,.
《2026年高三数学上学期专题训练:数列》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D A C B B AB ABD
题号 11
答案 ACD
1.C
【分析】举反例判断A,利用导数求函数的最小值,判断B,结合充分条件的定义判断C,举反例判断D.
【详解】对于A,当,满足,故A错误;
对于B,设,则,所以当时,;
当时,,即,故B错误;
对于C,由于是的充分条件,所以且,所以,即,故C正确;
对于D,当时,结论不成立,故D错误.
故选:C.
2.C
【分析】由累加法及等比数列前和公式可得,即可得到.
【详解】由,知,
所以,即,
故,又适合上式,故.
故选:C.
3.D
【分析】化简递推关系可得,证明数列为常数数列,由此求出,进而求解即可..
【详解】由,则,
所以,则数列为常数列,
又,则,即,为递增数列,
因为,,
所以使得成立的最小自然数为8.
故选:D.
4.D
【分析】由等比数列前项和的性质,成等比,公比为,结合即可求公比.
【详解】设等比数列的公比为,
根据等比数列前项和的性质,成等比,且公比为,
又,即,所以,
解得.
故选:D.
5.A
【分析】化简表达式,求出首项和公比,即可求出.
【详解】由题意,,
在等比数列中,,
设公比为q,
,解得,
∴,
当时,,解得:,
∴是以2为首项,3为公比的等比数列,
∴.
故选:A.
6.C
【分析】根据给定条件,利用等比数列性质及对数运算计算得解.
【详解】等比数列的各项均为正数,且,
.
故选:C
7.B
【分析】根据等差数列的定义求解即可.
【详解】设的公差为,则,,
故.
故选:B.
8.B
【分析】由题意,,两式相减求出数列的通项公式,再结合对数的运算性质判断ABD,设,记,利用导数可得在上恒成立,进而利用放缩判断C.
【详解】因为,
所以,
两式相减得,则,
则,所以,A说法错误;
,,而,故B说法正确;
设,记,则
故,即在上恒成立,
所以,故C错误;
,
所以,故不是递增数列,D说法错误;
故选:B
9.AB
【分析】利用等差数列的通项公式和求和公式进行运算,即可得到判断.
【详解】设等差数列的公差为,则,故B正确;
所以,故A正确;
,故C错误;
由,可得,
由于二次函数的对称轴为,开口向上,
所以当或时,最小,故D错误;
故选:AB
10.ABD
【分析】对于选项A,B,将递推数列构造成一个函数,然后对函数求导并判断单调性,从而可验证A,B的正确性;对于选项C,构造新函数,对新函数求导,判断函数的单调性,进而可判断的大小;对于选项D,基于C中构造的新函数的单调性,即可判断不等式的成立.
【详解】令,所以,
当,;当,,
所以在上单调递减,在上单调递增,
所以,又,
所以,,…,,
所以是中最小的项.
且对任意的,,都有,故A,B正确;
令,,
所以,所以在上单调递减,所以,
所以即;即,…,即,
综上所述,是中最大的项,所以不可能使得,,成等差数列,故C错误;
因为当,,,所以,
所以,即,
所以对任意的,,都有,故D正确.
故选:ABD.
11.ACD
【分析】根据给定的递推公式,依次计算判断A;变形给定的递推公式,结合等差数列定义判断BCD.
【详解】对于A,由,得,A正确;
对于BC,由,得,
则,数列是首项为,公差为的等差数列,B错误,C正确;
对于D,,则,解得,D正确.
故选:ACD
12.
【分析】结合给定递推关系构造等比数列,进而求出即可.
【详解】由,得,
由于,因此是首项为,公比为的等比数列,
从而可得,则.
故答案为:.
13.
【分析】由题意可知数列是首项为10,公差为的等差数列,求出前n项和,转化为求函数的最大值问题即可.
【详解】当时,,且,
所以,数列是首项为10,公差为的等差数列,
则数列的前n项和为,
因,故当时,取得最大值18.
故答案为:.
14.
【分析】因式分解后可得,则可得数列为等差数列,再利用等差数列的性质计算即可得解.
【详解】因为,
化简可得,
则,即,
所以数列为等差数列,所以,
所以,所以.
故答案为:.
15.(1)
(2)
【分析】(1)利用构造法可求的通项公式;
(2)利用参变分离和数列的单调性可求的最大项,从而可求参数的取值范围.
【详解】(1)数列的首项,可得,
而,故,故,
即数列是首项和公比均为3的等比数列,可得,即.
(2)若恒成立,即为,即恒成立,
设,可得,.
即数列是单调递减数列,可得,
所以,即实数的取值范围是
16.(1)
(2)
【分析】(1)根据之间的关系计算;
(2)由(1)可知,然后使用裂项相消求和即可.
【详解】(1)由题可知:,当时,,
由①,当时,②;
①-②得:,
所以,即,
所以数列是以2为首项,2为公差得等差数列.
所以,即;
(2)由(1)可知:,
所以,
所以,
则.
17.(1),,
(2)证明见解析
(3),
【分析】(1)分别令,可计算出结果;
(2)选①依题意得到,然后变形可得;选②依题意(3)得到当时,,然后得到,变形即可;
选择①、②由(2)可知,然后使用错位相减法求和.
【详解】(1)(1)令,得.又,所以.
.
令,得.又,所以.
故.
(2)若选择①:由已知,得.
故,所以,.
故是首项和公比均为2的等比数列.
若选择②:由已知,.故当时,.
两式相减,得.
化简并整理,得(,且).
又,,所以.
故是以1为首项,2为公比等比数列.
(3)若选择①:由(2)知,,故.
若选择②:由(2)知,,故.
所以.
所以.
则.
两式错位相减,得.
所以,
18.(1)成等比数列,理由见解析
(2)证明见解析
(3)证明见解析
【分析】(1)根据题意,令,和,依次求出,利用等比数列定义判断即可;
(2)由,,成公差为的等差数列,得,即可利用累加法求出,从而可得,,,再利用等比数列定义判断即可;
(3)当为奇数时,,,当为偶数时,,,利用放缩法求出数列的前项和为,即可证明.
【详解】(1)当时,成公差为1的等差数列,
则,;
当时,成公差为2的等差数列,则,;
当时,成公差为3的等差数列,则.
所以,,从而,故成等比数列.
(2)由,,成公差为的等差数列,得,
可得:,,,,,
累加得
因为,,成公差为的等差数列,所以,
,又因为,,成公差为的等差数列,
所以,
所以,得,,成等比数列.
(3)由,由(2)知:
当为奇数时,,,
当为偶数时,,,
故,且对一切正整数,有,
时,
,
综上,.
19.(1),;,
(2)(ⅰ)证明见解析;(ⅱ)证明见解析
【分析】(1)由等差数列和等比数列的通项公式进行计算;
(2)
(ⅰ)根据,写出并计算,由证明出是等比数列;
(ⅱ)由,设出,用错位相减得出,从而证明.
【详解】(1)因为等差数列的第2项为3,其前5项和为25.
所以,,
计算得,公差为,
所以;
设等比数列的公比为,因为,所以,
解得或(舍),故;
(2)(ⅰ)由题意,,
所以,
所以,且,所以数列是以4为公比的等比数列;
(ⅱ)由题意知,,
所以,所以,
设,则,
两式相减得,
所以,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年高三数学上学期专题训练:数列
一、单选题
1.(2025·江西新余·模拟预测)下列说法正确的是( )
A.已知,则且
B.命题“”是真命题
C.是的充分条件,则
D.若等比数列的通项公式为,则其前项和
2.(2025·江西新余·模拟预测)已知数列满足,且,则数列的通项公式为( )
A. B.
C. D.
3.(2025·四川广安·模拟预测)已知数列满足,,则使得成立的最小自然数为( )
A.5 B.6 C.7 D.8
4.(2025·四川成都·一模)记为等比数列的前项和,若,则的公比为( )
A.2 B. C. D.
5.(2025·江苏连云港·模拟预测)已知等比数列的前项和为,且,则( )
A. B. C. D.
6.(2025·云南丽江·模拟预测)已知等比数列的各项均为正数,且,则( )
A.2014 B.2024 C.2025 D.2026
7.(2025·广东惠州·模拟预测)已知等差数列的首项,公差,在中每相邻两项之间都插入3个数,组成一个新的等差数列,则( )
A. B.
C. D.
8.(2025·四川绵阳·模拟预测)已知数列满足,,,则下列选项正确的是( )
A. B. C. D.是递增数列
二、多选题
9.(2025·海南三亚·一模)数列为等差数列,为其前项和,已知,则( )
A. B.
C. D.当或时,最大
10.(2025·河南许昌·模拟预测)已知数列满足,,则下列说法正确的是( )
A.为中的最小项
B.对任意的,,都有
C.存在,使得,,成等差数列
D.对任意的,,都有
11.(2025·广西河池·二模)已知数列满足且,则下列说法正确的是( )
A.
B.数列是周期数列
C.是等差数列
D.数列的通项公式为
三、填空题
12.(2025·云南临沧·模拟预测)已知数列中,,,,则数列的通项公式为 .
13.(2025·四川绵阳·模拟预测)已知数列中,,,则数列的前n项和的最大值等于
14.(2025·河北邢台·二模)已知数列的前n项和为,且,,则 .
四、解答题
15.(2025·江西·模拟预测)已知数列的首项.
(1)求数列的通项公式;
(2)若恒成立,求实数的取值范围.
16.(2024·河北·模拟预测)记为各项均为正数的数列的前项和,已知.
(1)求数列的通项公式;
(2)若数列满足,求数列的前项和.
17.(2025·四川成都·一模)记为数列的前项和,已知,且.
(1)求,,;
(2)在下列两个结论中,任选一个加以证明;(若两个都证明,以首选计分)
①是等比数列;②是等比数列.
(3)记为数列的前项和,求.
18.(2025·江苏连云港·模拟预测)在数列中,,对于,,,成等差数列,其公差为.
(1)判断是否成等比数列?并说明理由;
(2)证明:,,成等比数列;
(3)设,数列的前项和为,证明:.
19.(2025·湖南长沙·三模)已知等差数列的第2项为3,其前5项和为25.数列是公比大于0的等比数列,,.
(1)求和的通项公式;
(2)记,,
(ⅰ)证明是等比数列;
(ⅱ)证明,.
《2026年高三数学上学期专题训练:数列》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D A C B B AB ABD
题号 11
答案 ACD
1.C
【分析】举反例判断A,利用导数求函数的最小值,判断B,结合充分条件的定义判断C,举反例判断D.
【详解】对于A,当,满足,故A错误;
对于B,设,则,所以当时,;
当时,,即,故B错误;
对于C,由于是的充分条件,所以且,所以,即,故C正确;
对于D,当时,结论不成立,故D错误.
故选:C.
2.C
【分析】由累加法及等比数列前和公式可得,即可得到.
【详解】由,知,
所以,即,
故,又适合上式,故.
故选:C.
3.D
【分析】化简递推关系可得,证明数列为常数数列,由此求出,进而求解即可..
【详解】由,则,
所以,则数列为常数列,
又,则,即,为递增数列,
因为,,
所以使得成立的最小自然数为8.
故选:D.
4.D
【分析】由等比数列前项和的性质,成等比,公比为,结合即可求公比.
【详解】设等比数列的公比为,
根据等比数列前项和的性质,成等比,且公比为,
又,即,所以,
解得.
故选:D.
5.A
【分析】化简表达式,求出首项和公比,即可求出.
【详解】由题意,,
在等比数列中,,
设公比为q,
,解得,
∴,
当时,,解得:,
∴是以2为首项,3为公比的等比数列,
∴.
故选:A.
6.C
【分析】根据给定条件,利用等比数列性质及对数运算计算得解.
【详解】等比数列的各项均为正数,且,
.
故选:C
7.B
【分析】根据等差数列的定义求解即可.
【详解】设的公差为,则,,
故.
故选:B.
8.B
【分析】由题意,,两式相减求出数列的通项公式,再结合对数的运算性质判断ABD,设,记,利用导数可得在上恒成立,进而利用放缩判断C.
【详解】因为,
所以,
两式相减得,则,
则,所以,A说法错误;
,,而,故B说法正确;
设,记,则
故,即在上恒成立,
所以,故C错误;
,
所以,故不是递增数列,D说法错误;
故选:B
9.AB
【分析】利用等差数列的通项公式和求和公式进行运算,即可得到判断.
【详解】设等差数列的公差为,则,故B正确;
所以,故A正确;
,故C错误;
由,可得,
由于二次函数的对称轴为,开口向上,
所以当或时,最小,故D错误;
故选:AB
10.ABD
【分析】对于选项A,B,将递推数列构造成一个函数,然后对函数求导并判断单调性,从而可验证A,B的正确性;对于选项C,构造新函数,对新函数求导,判断函数的单调性,进而可判断的大小;对于选项D,基于C中构造的新函数的单调性,即可判断不等式的成立.
【详解】令,所以,
当,;当,,
所以在上单调递减,在上单调递增,
所以,又,
所以,,…,,
所以是中最小的项.
且对任意的,,都有,故A,B正确;
令,,
所以,所以在上单调递减,所以,
所以即;即,…,即,
综上所述,是中最大的项,所以不可能使得,,成等差数列,故C错误;
因为当,,,所以,
所以,即,
所以对任意的,,都有,故D正确.
故选:ABD.
11.ACD
【分析】根据给定的递推公式,依次计算判断A;变形给定的递推公式,结合等差数列定义判断BCD.
【详解】对于A,由,得,A正确;
对于BC,由,得,
则,数列是首项为,公差为的等差数列,B错误,C正确;
对于D,,则,解得,D正确.
故选:ACD
12.
【分析】结合给定递推关系构造等比数列,进而求出即可.
【详解】由,得,
由于,因此是首项为,公比为的等比数列,
从而可得,则.
故答案为:.
13.
【分析】由题意可知数列是首项为10,公差为的等差数列,求出前n项和,转化为求函数的最大值问题即可.
【详解】当时,,且,
所以,数列是首项为10,公差为的等差数列,
则数列的前n项和为,
因,故当时,取得最大值18.
故答案为:.
14.
【分析】因式分解后可得,则可得数列为等差数列,再利用等差数列的性质计算即可得解.
【详解】因为,
化简可得,
则,即,
所以数列为等差数列,所以,
所以,所以.
故答案为:.
15.(1)
(2)
【分析】(1)利用构造法可求的通项公式;
(2)利用参变分离和数列的单调性可求的最大项,从而可求参数的取值范围.
【详解】(1)数列的首项,可得,
而,故,故,
即数列是首项和公比均为3的等比数列,可得,即.
(2)若恒成立,即为,即恒成立,
设,可得,.
即数列是单调递减数列,可得,
所以,即实数的取值范围是
16.(1)
(2)
【分析】(1)根据之间的关系计算;
(2)由(1)可知,然后使用裂项相消求和即可.
【详解】(1)由题可知:,当时,,
由①,当时,②;
①-②得:,
所以,即,
所以数列是以2为首项,2为公差得等差数列.
所以,即;
(2)由(1)可知:,
所以,
所以,
则.
17.(1),,
(2)证明见解析
(3),
【分析】(1)分别令,可计算出结果;
(2)选①依题意得到,然后变形可得;选②依题意(3)得到当时,,然后得到,变形即可;
选择①、②由(2)可知,然后使用错位相减法求和.
【详解】(1)(1)令,得.又,所以.
.
令,得.又,所以.
故.
(2)若选择①:由已知,得.
故,所以,.
故是首项和公比均为2的等比数列.
若选择②:由已知,.故当时,.
两式相减,得.
化简并整理,得(,且).
又,,所以.
故是以1为首项,2为公比等比数列.
(3)若选择①:由(2)知,,故.
若选择②:由(2)知,,故.
所以.
所以.
则.
两式错位相减,得.
所以,
18.(1)成等比数列,理由见解析
(2)证明见解析
(3)证明见解析
【分析】(1)根据题意,令,和,依次求出,利用等比数列定义判断即可;
(2)由,,成公差为的等差数列,得,即可利用累加法求出,从而可得,,,再利用等比数列定义判断即可;
(3)当为奇数时,,,当为偶数时,,,利用放缩法求出数列的前项和为,即可证明.
【详解】(1)当时,成公差为1的等差数列,
则,;
当时,成公差为2的等差数列,则,;
当时,成公差为3的等差数列,则.
所以,,从而,故成等比数列.
(2)由,,成公差为的等差数列,得,
可得:,,,,,
累加得
因为,,成公差为的等差数列,所以,
,又因为,,成公差为的等差数列,
所以,
所以,得,,成等比数列.
(3)由,由(2)知:
当为奇数时,,,
当为偶数时,,,
故,且对一切正整数,有,
时,
,
综上,.
19.(1),;,
(2)(ⅰ)证明见解析;(ⅱ)证明见解析
【分析】(1)由等差数列和等比数列的通项公式进行计算;
(2)
(ⅰ)根据,写出并计算,由证明出是等比数列;
(ⅱ)由,设出,用错位相减得出,从而证明.
【详解】(1)因为等差数列的第2项为3,其前5项和为25.
所以,,
计算得,公差为,
所以;
设等比数列的公比为,因为,所以,
解得或(舍),故;
(2)(ⅰ)由题意,,
所以,
所以,且,所以数列是以4为公比的等比数列;
(ⅱ)由题意知,,
所以,所以,
设,则,
两式相减得,
所以,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
