1.6 利用三角函数测高 课件(共15张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 09:35:03 | ||
图片预览



文档简介
(共15张PPT)
1.6 利用三角函数测高
1.在Rt △ABC中,∠C=90°,已知a, ∠A的值,
则c的值为 ( )
A. atanA B. asinA C. D.
2.在Rt△ABC中,∠C=90°,∠A=45°, a= 3,
则b=_____,c=______,∠B=______
一、交流预习
D
3
45°
一、交流预习
1、如何利用测倾器测量出目标M的角度?
2、怎样测量底部可以到达的物体MN的高度,你会设计方案吗?
如何根据测量数据,求MN的高度,说说你的理由。
3、怎样测量底部不可以到达的物体MN的高度,你会设计方案吗?
如何根据测量数据,求MN的高度,说说你的理由。
请把你预习中的疑惑与师傅交流
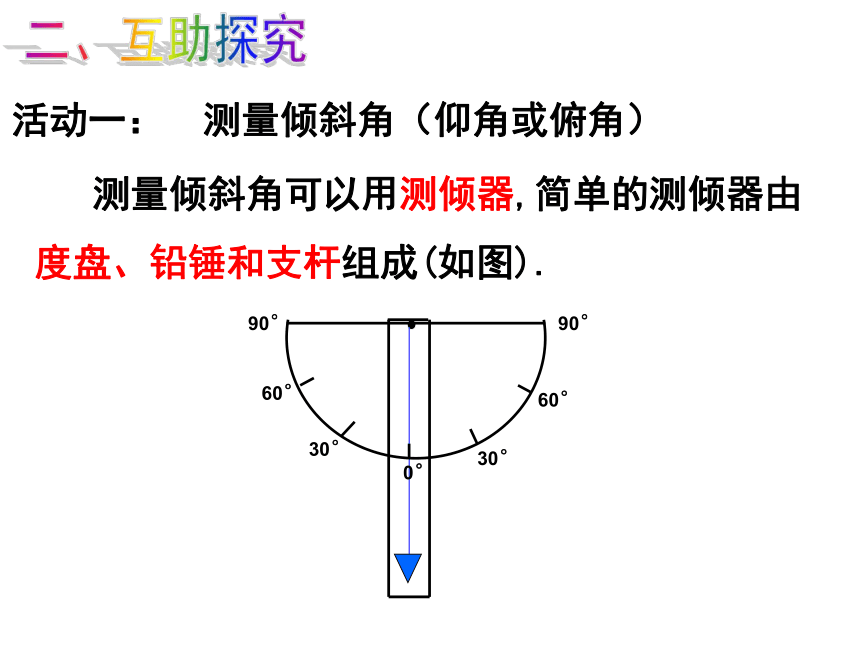
活动一: 测量倾斜角(仰角或俯角)
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
30°
0°
60°
90°
90°
60°
30°
二、互助探究
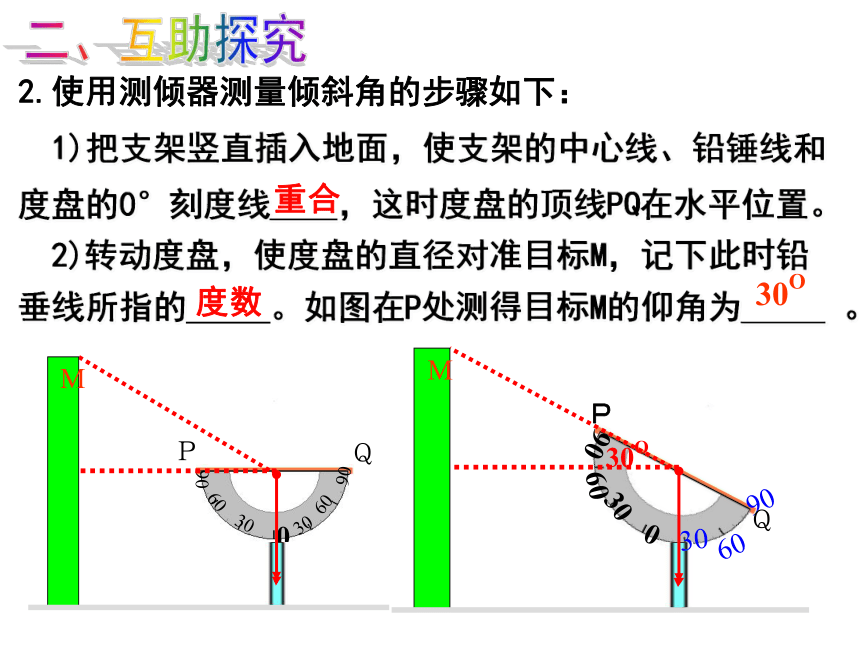
2.使用测倾器测量倾斜角的步骤如下:
1)把支架竖直插入地面,使支架的中心线、铅锤线和
度盘的0°刻度线 ,这时度盘的顶线PQ在水平位置。
2)转动度盘,使度盘的直径对准目标M,记下此时铅
垂线所指的 。如图在P处测得目标M的仰角为 。
0
30
30
60
60
90
90
M
P
Q
M
0
30
30
60
60
90
90
P
Q
重合
度数
30O
30O
二、互助探究
A
C
M
N
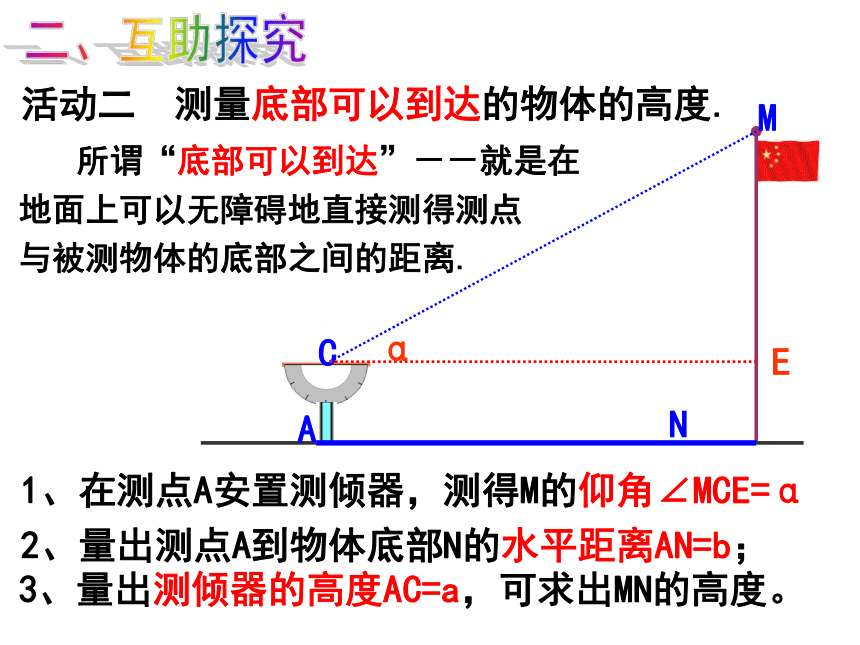
1、在测点A安置测倾器,测得M的仰角∠MCE=α
E
2、量出测点A到物体底部N的水平距离AN=b;
3、量出测倾器的高度AC=a,可求出MN的高度。
α
所谓“底部可以到达”--就是在
地面上可以无障碍地直接测得测点
与被测物体的底部之间的距离.
活动二 测量底部可以到达的物体的高度.
二、互助探究
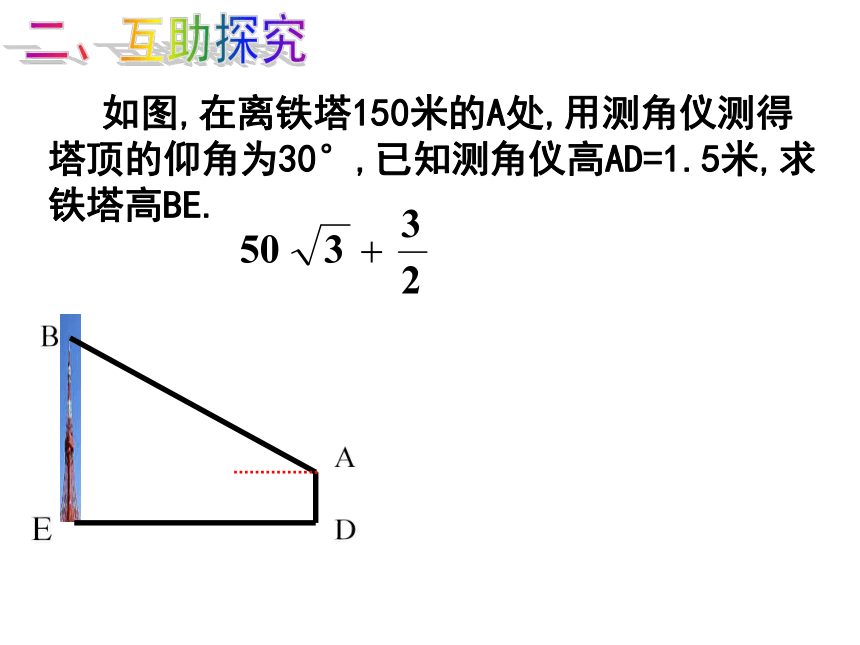
如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.
E
B
A
D
二、互助探究
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
要测量物体MN的高度,使用测倾器测一次仰角够吗?
a
α
E
C
A
N
M
活动三 测量底部不可以到达的物体的高度.
二、互助探究
1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2、在测点A与物体之间的B处安置测倾器(A、B、N在同一直线上),测得此时M的仰角∠MDE=β;
β
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
活动三 测量底部不可以
到达的物体的高度.
b
a
a
二、互助探究
三、分层提高
2、小亮实习报告的部分内容:
(1)请根据小亮测得的数据,∠α= ,
∠β=45度,CD=60m
(2)已知测倾器的高CE=DF=1m.计算
地王大厦的高度(精确到1m).
C
E
D
F
A
G
B
α
β
30°
1、如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她和树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树的高度是_____m.
83m
这节课我们都
学了哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
我想对我的师傅
(学友)说……
温馨提示:从知识、学法方面和师友互助方面进行总结
四、归纳总结
本课主要学习测量物体的高度的方法:
1.测量底部可以到达的物体的高度.
2.测量底部不可以到达的物体的高度.
3.目前我们学习的测量物体高度的方法有
四、归纳总结
利用“相似三角形、全等三角形、三角函数”等有关知识
五、巩固反馈
如图,某校数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(C,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(≈1.73,结果精确到0.1米)
22.4m
五、巩固反馈
巩固性作业:
1、完成课本P25~P26
2、如何测量“我们学校旗杆高度”?你会设计测量方案吗?你有几种不同测量方法?说说你的理由。
总结归纳:
总结本章知识点,并画出思维导图。
帮助别人就是帮助自己!
师友互助,共同进步!
1.6 利用三角函数测高
1.在Rt △ABC中,∠C=90°,已知a, ∠A的值,
则c的值为 ( )
A. atanA B. asinA C. D.
2.在Rt△ABC中,∠C=90°,∠A=45°, a= 3,
则b=_____,c=______,∠B=______
一、交流预习
D
3
45°
一、交流预习
1、如何利用测倾器测量出目标M的角度?
2、怎样测量底部可以到达的物体MN的高度,你会设计方案吗?
如何根据测量数据,求MN的高度,说说你的理由。
3、怎样测量底部不可以到达的物体MN的高度,你会设计方案吗?
如何根据测量数据,求MN的高度,说说你的理由。
请把你预习中的疑惑与师傅交流
活动一: 测量倾斜角(仰角或俯角)
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
30°
0°
60°
90°
90°
60°
30°
二、互助探究
2.使用测倾器测量倾斜角的步骤如下:
1)把支架竖直插入地面,使支架的中心线、铅锤线和
度盘的0°刻度线 ,这时度盘的顶线PQ在水平位置。
2)转动度盘,使度盘的直径对准目标M,记下此时铅
垂线所指的 。如图在P处测得目标M的仰角为 。
0
30
30
60
60
90
90
M
P
Q
M
0
30
30
60
60
90
90
P
Q
重合
度数
30O
30O
二、互助探究
A
C
M
N
1、在测点A安置测倾器,测得M的仰角∠MCE=α
E
2、量出测点A到物体底部N的水平距离AN=b;
3、量出测倾器的高度AC=a,可求出MN的高度。
α
所谓“底部可以到达”--就是在
地面上可以无障碍地直接测得测点
与被测物体的底部之间的距离.
活动二 测量底部可以到达的物体的高度.
二、互助探究
如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.
E
B
A
D
二、互助探究
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
要测量物体MN的高度,使用测倾器测一次仰角够吗?
a
α
E
C
A
N
M
活动三 测量底部不可以到达的物体的高度.
二、互助探究
1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2、在测点A与物体之间的B处安置测倾器(A、B、N在同一直线上),测得此时M的仰角∠MDE=β;
β
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
活动三 测量底部不可以
到达的物体的高度.
b
a
a
二、互助探究
三、分层提高
2、小亮实习报告的部分内容:
(1)请根据小亮测得的数据,∠α= ,
∠β=45度,CD=60m
(2)已知测倾器的高CE=DF=1m.计算
地王大厦的高度(精确到1m).
C
E
D
F
A
G
B
α
β
30°
1、如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她和树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树的高度是_____m.
83m
这节课我们都
学了哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
我想对我的师傅
(学友)说……
温馨提示:从知识、学法方面和师友互助方面进行总结
四、归纳总结
本课主要学习测量物体的高度的方法:
1.测量底部可以到达的物体的高度.
2.测量底部不可以到达的物体的高度.
3.目前我们学习的测量物体高度的方法有
四、归纳总结
利用“相似三角形、全等三角形、三角函数”等有关知识
五、巩固反馈
如图,某校数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(C,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(≈1.73,结果精确到0.1米)
22.4m
五、巩固反馈
巩固性作业:
1、完成课本P25~P26
2、如何测量“我们学校旗杆高度”?你会设计测量方案吗?你有几种不同测量方法?说说你的理由。
总结归纳:
总结本章知识点,并画出思维导图。
帮助别人就是帮助自己!
师友互助,共同进步!
