6.4 线段的和差 课件(共44张PPT)
文档属性
| 名称 | 6.4 线段的和差 课件(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:22:22 | ||
图片预览










文档简介
(共44张PPT)
6.4 线段的和差
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
线段的和差
课程目标
理解线段和差的概念,能结合图形明确线段和差的几何意义。
掌握线段和差的计算方法,能运用图形中线段的位置关系进行和差运算。
学会利用线段中点等条件解决与线段和差相关的问题,提高几何推理和计算能力。
线段的和
定义
如果一条线段可以看作是由另外两条线段首尾顺次连接组成的,那么这条线段就是另外两条线段的和。
几何表示:如图,在线段\(AC\)上,点\(B\)在\(A\)、\(C\)之间,线段\(AB\)和线段\(BC\)首尾顺次连接组成了线段\(AC\),那么\(AC = AB + BC\)。
实例:一根长\(5\)厘米的线段和一根长\(3\)厘米的线段,首尾相接后组成的线段长就是\(5 + 3 = 8\)厘米,这根\(8\)厘米的线段就是前两条线段的和。
计算方法
已知两条线段的长度,求它们的和,直接将两条线段的长度相加即可;若已知一条线段及其中一部分线段的长度,求另一部分线段的长度(和的逆运算),用和减去已知部分的长度。
例 1:已知线段\(AB = 4\)厘米,线段\(BC = 3\)厘米,且点\(B\)在\(A\)、\(C\)之间,求\(AC\)的长度。
解:因为\(AC = AB + BC\),所以\(AC = 4 + 3 = 7\)厘米。
例 2:已知线段\(AC = 10\)厘米,线段\(AB = 6\)厘米,点\(B\)在\(A\)、\(C\)之间,求\(BC\)的长度。
解:因为\(AC = AB + BC\),所以\(BC = AC - AB = 10 - 6 = 4\)厘米。
线段的差
定义
如果一条线段可以看作是由一条较长的线段去掉其中一部分线段后剩余的部分,那么这条线段就是两条线段的差。
几何表示:如图,在线段\(AB\)上,点\(C\)在\(A\)、\(B\)之间,从线段\(AB\)中去掉线段\(AC\)后,剩余的线段\(CB\)就是\(AB\)与\(AC\)的差,即\(CB = AB - AC\)。
实例:一根长\(7\)厘米的线段,去掉其中\(3\)厘米长的一部分后,剩余部分的长度是\(7 - 3 = 4\)厘米,这\(4\)厘米的线段就是原来线段与去掉部分线段的差。
计算方法
已知两条线段的长度(较长线段和较短线段),求它们的差,用较长线段的长度减去较短线段的长度;若已知线段的差及其中一条线段的长度,求另一条线段的长度,根据差的关系进行计算。
例 1:已知线段\(AB = 8\)厘米,线段\(AC = 5\)厘米,点\(C\)在\(A\)、\(B\)之间,求\(BC\)的长度。
解:因为\(BC = AB - AC\),所以\(BC = 8 - 5 = 3\)厘米。
例 2:已知线段\(DE = 4\)厘米,\(DF - DE = 3\)厘米,且点\(E\)在\(D\)、\(F\)之间,求\(DF\)的长度。
解:因为\(DF - DE = 3\),所以\(DF = DE + 3 = 4 + 3 = 7\)厘米。
线段和差与中点的综合应用
当涉及线段中点时,可利用中点将线段分成相等的两部分的性质,结合线段的和差进行计算。
例 1:如图,点\(M\)是线段\(AB\)的中点,点\(N\)是线段\(BC\)的中点,\(AB = 6\)厘米,\(BC = 4\)厘米,求\(MN\)的长度。
解:因为点\(M\)是\(AB\)的中点,所以\(BM = \frac{1}{2}AB = \frac{1}{2} 6 = 3\)厘米。
因为点\(N\)是\(BC\)的中点,所以\(BN = \frac{1}{2}BC = \frac{1}{2} 4 = 2\)厘米。
又因为\(MN = BM + BN\),所以\(MN = 3 + 2 = 5\)厘米。
例 2:线段\(AC = 12\)厘米,点\(B\)是线段\(AC\)上一点,且\(AB = 5\)厘米,点\(D\)是线段\(AB\)的中点,点\(E\)是线段\(AC\)的中点,求\(DE\)的长度。
解:因为点\(E\)是\(AC\)的中点,所以\(AE = \frac{1}{2}AC = \frac{1}{2} 12 = 6\)厘米。
因为点\(D\)是\(AB\)的中点,所以\(AD = \frac{1}{2}AB = \frac{1}{2} 5 = 2.5\)厘米。
又因为\(DE = AE - AD\),所以\(DE = 6 - 2.5 = 3.5\)厘米。
复杂图形中线段和差的计算
在较复杂的图形中,需要先明确各线段之间的位置关系,找出已知线段和未知线段之间的和差关系,再进行计算。
例:如图,线段\(AB = 10\)厘米,点\(C\)在\(AB\)的延长线上,\(BC = 4\)厘米,点\(D\)在\(AB\)上,\(AD = 3\)厘米,求\(CD\)的长度。
解:由图可知,\(CD = DA + AB + BC\)(因为点\(C\)在\(AB\)延长线上,点\(D\)在\(AB\)上)。
代入数值可得:\(CD = 3 + 10 + 4 = 17\)厘米。
线段和差的应用
测量问题:在无法直接测量某条线段长度时,可通过测量与之相关的两条线段的长度,利用和差关系求出该线段的长度。例如,测量池塘两端的距离,可在池塘外选一点,测量这点到池塘两端的距离,再根据位置关系用和差计算。
工程建设:在道路施工中,已知两段道路的长度,可通过和差计算总长度;若已知总长度和其中一段的长度,可求出另一段的长度,以合理安排施工。
物品拼接:将几根短线段拼接成一根长线段,长线段的长度就是各短线段长度的和;将一根长线段截成几段,每段的长度可通过长线段与其他段长度的差求得。
课堂练习
已知线段\(AB = 7\)厘米,线段\(BC = 3\)厘米,点\(B\)在\(A\)、\(C\)之间,求\(AC\)的长度。
线段\(MN = 15\)厘米,线段\(MP = 9\)厘米,点\(P\)在\(M\)、\(N\)之间,求\(PN\)的长度。
点\(O\)是线段\(EF\)的中点,\(EG = 2\)厘米,\(GF = 6\)厘米,求\(EO\)的长度。
线段\(AB = 20\)厘米,点\(C\)在\(AB\)上,\(AC = 8\)厘米,点\(D\)是\(AC\)的中点,点\(E\)是\(CB\)的中点,求\(DE\)的长度。
总结
线段的和是指一条线段由另外两条线段首尾顺次连接组成,其长度为两条线段长度之和;线段的差是指一条线段由较长线段去掉一部分后剩余,其长度为较长线段与该部分线段长度之差。
计算线段和差时,要明确线段的位置关系,结合图形找出和差关系,若有中点,可利用中点性质将线段等分后再计算。
线段和差在实际测量、工程建设等领域有重要应用,掌握其计算方法有助于解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解线段的和差的意义,会用直尺和圆规作两条线段的
和与差,发展几何直观。
2.理解线段的中点的概念,会用刻度尺二等分线段。
3.会进行有关线段的和、差、倍、分的简单计算,发展
推理能力。
两条线段的和 两条线段的差(两条线段的和或
差仍是一条线段)
概念 如果一条线段的长度是 另两条线段的长度的 和,那么这条线段就叫 作另两条线段的和。 如果一条线段的长度是另两条线
段的长度的差,那么这条线段就
叫作另两条线段的差。
条件 ___________________________________________________________ 图形 _____________________________________________________ __________________________________
作法
结论
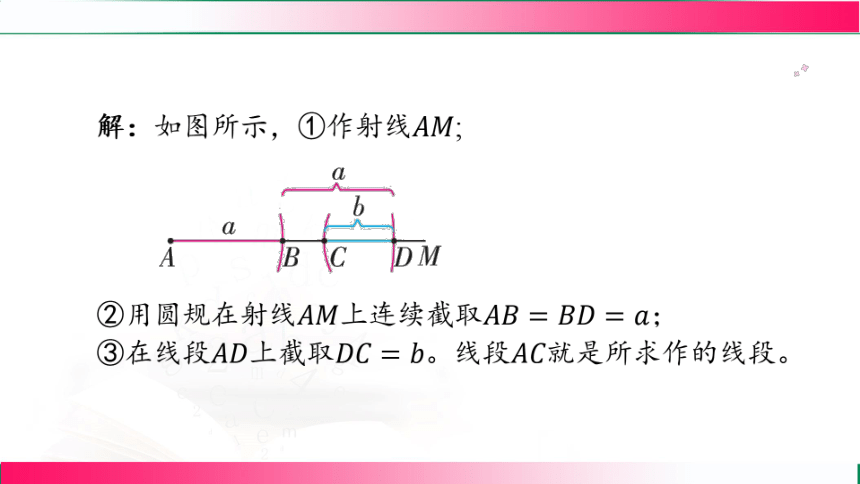
典例1 如图,已知线段, ,用直尺和圆
规作线段,使 。
解:如图所示,①作射线 ;
②用圆规在射线上连续截取 ;
③在线段上截取。线段 就是所求作的线段。
概念
几何表述
图示 ____________________________________________________
若点是线段的中点,则点一定在线段 上。
教材延伸
线段的三等分点、四等分点
将线段分成相等的三条线段,,,点,即线段 的
三等分点。同样还可以得到线段的四等分点等。如图所示。
类似地,还有线段的五等分点、六等分点等。
典例2 下列说法正确的是( )
D
A.若,则点为线段 的中点
B.若,则点为线段 的中点
C.若,则点为线段 的中点
D.若,则点为线段 的中点
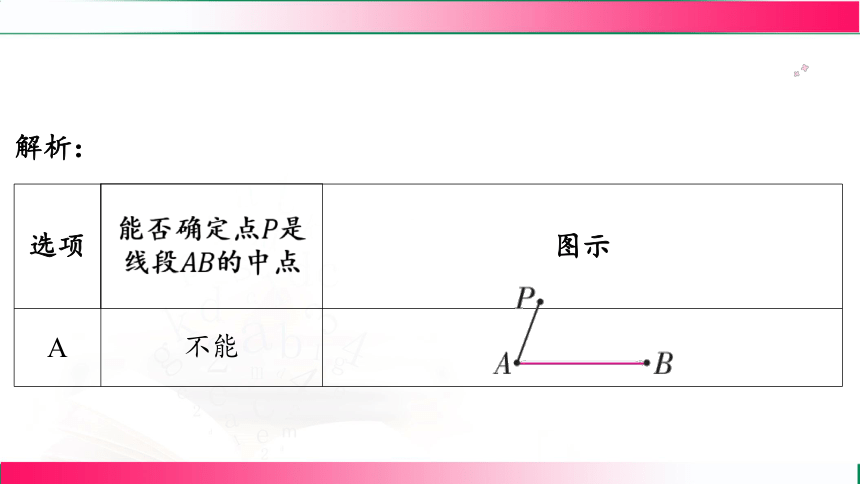
解析:
选项 图示
A 不能 _____________________________________
选项 图示
B 不能
选项 图示
C 不能 _________________________________________
D 能 _________________________________
知识过关
①一般地,如果一条线段的长度是另两条线段的长度的和,那
么这条线段就叫作另 两条线段的和 ;如果一条线段的长
度是另两条线段的长度的差,那么这条线段就叫作另 两条
线段的差 .
②点C把线段AB分成相等的两条线段AC与BC,点C叫作线
段AB的 中点 .这时,AC= BC = AB ,AB
= 2AC = 2BC .
两条线段的和
两条
线段的差
中点
BC
AB
2AC
2BC
线段的和差
1. [2024·杭州余杭区期末]如图,下列关系式中与图不一定符
合的式子是( C )
A. AD-CD=AB+BC
B. AC-BC=AD-BD
C. AC-BC=BD-BC
D. AC-AB=BD-CD
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 线段AB的长为2 cm,延长AB到C,使AC=3AB,再延
长BA到D,使BD=2BC,则线段CD的长为( D )
A. 10 cm B. 8 cm
C. 6 cm D. 12 cm
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024·西安模拟]若点P在线段AB的延长线上,AP=8,
BP=3,则AB的长为 .
4. 已知点C,D在线段AB上,且AC=BD=1.5,若AB
=7,则CD的长为 .
5
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
尺规作图作线段的和差
5. 如图,已知线段a,b,画一条射线OM,在射线OM上
依次截取OA=AB=a,在线段BO上截取BC=b.则
( D )
A. OB=a+b B. OB=2b-a
C. OC=b-a D. OC=2a-b
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [母题 教材P175作业题T2]如图,已知线段a,b,用尺规
作一条线段c,使c=2a+b.(保留作图痕迹,不写作法)
【解】如答图所示:AE=2a+b=c.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
线段的中点
7. [2024·台州温岭期末]如图,M是线段AB的中点,N是线
段BM上一点,下列各式可以表示MN的长度的是
( B )
A. AB-BN B. AN-BM
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [母题 教材P174例2]如图,点M是AB的中点,点N是BD
的中点,AB=6 cm,BC=10 cm,CD=8 cm.则MN的
长为( A )
A. 12 cm B. 11 cm
C. 13 cm D. 10 cm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以BM=AM= AB= ×6=3(cm).
因为BC=10 cm,CD=8 cm,
所以BD=BC+CD=10+8=18(cm).
因为点N是BD的中点,
【点拨】
因为点M是AB的中点,AB=6 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以BN=DN= BD= ×18=9(cm),
所以MN=MB+BN=3+9=12(cm).
故选:A.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [2024·湖州期末]两根木条,一根长10 cm,另一根长12 cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为 cm.
11或1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [2024·绍兴诸暨期末]如图,M是线段AB的中点,点C
在线段AB上,N是线段AC的中点,且AN=2 cm,
CM=1 cm,求线段AB的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】因为N是线段AC的中点,且AN=2 cm,
所以NC=2 cm.
因为CM=1 cm,所以AM=5 cm.
因为M是线段AB的中点,
所以AB=2AM=10 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[易错题]点与线段的位置未分类讨论而出错
11. [2024·无锡期末]已知线段AB=7,点C为直线AB上一
点,且AC∶BC=4∶3,点D为线段AC的中点,则线段
BD的长为( C )
A. 5 B. 7
C. 5或7 D. 5.5或7
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [2024·菏泽期末]如图,C,D是线段AB上两点(点D
在点C右侧),E,F分别是线段AD,BC的中点.下列
结论:
①EF= AB;②若AE=BF,则AC=BD;③AB-
CD=2EF;④AC-BD=EC-DF. 其中正确的结论
是( B )
B
A. ①② B. ②③
C. ②④ D. ③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [新考向·知识情境化][2024·舟山调研] A,B,C三个住
宅区分别住有某公司职工30人、15人、10人,且这三个
住宅区在一条大道上(A,B,C三点共线),如图所示,
已知AB=100米,BC=200米,为了方便职工上下班,
该公司的接送车打算在此区间内设一个停靠点,为使所
有人步行到停靠点的路程之和最小,那么该停靠点的位
置应设在( A )
A
A. 点A B. 点B
C. 点A,B之间 D. 点B,C之间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. 如图,A,B,C,D是直线l上的四个点,M,N分
别是AB,CD的中点.
(1)如果MB=2 cm,NC=1.8 cm,BC=5 cm,则AD
的长为 cm;
12.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为MB=2 cm,NC=1.8 cm,
所以MB+NC=3.8 cm.
因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=
7.6 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以AD=AB+CD+BC=7.6+5=12.6(cm).
故答案为:12.6;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)如果MN=10 cm,BC=6 cm,则AD的长
为 cm;
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为MN=10 cm,BC=6 cm,
所以BM+CN=MN-BC=10-6=4(cm).
因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=8 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以AD=AB+CD+BC=8+6=14(cm).
故答案为:14;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)如果MN=a,BC=b,求AD的长.
【解】因为MN=a,BC=b,所以BM+CN=a-b.因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=2(a-
b),所以AD=AB+CD+BC=2(a-b)+b=2a-2b+b=2a-b.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. 已知线段AB,M,N分别是AC,BC的中点.
(1)如图,若点C在线段AB上,AC=12 cm,CB=9 cm,求线段MN的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】因为AC=12 cm,CB=9 cm,M,N分别是
AC,BC的中点,
所以CM= AC=6 cm,CN= BC=4.5 cm,
所以MN=CM+CN=6+4.5=10.5(cm);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若C为线段AB上任意一点,满足AC+CB=a cm,
你能猜出MN的长度吗?请说明理由.
【解】MN= cm,理由如下:
因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN=CM+CN= (AC+BC)= cm;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若点C在线段AB的延长线上,且满足AC-BC=
b cm,你能猜出MN的长度吗?请画出图形,写出你的
结论,并说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN=CM-CN= (AC-BC)= cm.
【解】如答图,MN= cm,理由如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
6.4 线段的和差
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
线段的和差
课程目标
理解线段和差的概念,能结合图形明确线段和差的几何意义。
掌握线段和差的计算方法,能运用图形中线段的位置关系进行和差运算。
学会利用线段中点等条件解决与线段和差相关的问题,提高几何推理和计算能力。
线段的和
定义
如果一条线段可以看作是由另外两条线段首尾顺次连接组成的,那么这条线段就是另外两条线段的和。
几何表示:如图,在线段\(AC\)上,点\(B\)在\(A\)、\(C\)之间,线段\(AB\)和线段\(BC\)首尾顺次连接组成了线段\(AC\),那么\(AC = AB + BC\)。
实例:一根长\(5\)厘米的线段和一根长\(3\)厘米的线段,首尾相接后组成的线段长就是\(5 + 3 = 8\)厘米,这根\(8\)厘米的线段就是前两条线段的和。
计算方法
已知两条线段的长度,求它们的和,直接将两条线段的长度相加即可;若已知一条线段及其中一部分线段的长度,求另一部分线段的长度(和的逆运算),用和减去已知部分的长度。
例 1:已知线段\(AB = 4\)厘米,线段\(BC = 3\)厘米,且点\(B\)在\(A\)、\(C\)之间,求\(AC\)的长度。
解:因为\(AC = AB + BC\),所以\(AC = 4 + 3 = 7\)厘米。
例 2:已知线段\(AC = 10\)厘米,线段\(AB = 6\)厘米,点\(B\)在\(A\)、\(C\)之间,求\(BC\)的长度。
解:因为\(AC = AB + BC\),所以\(BC = AC - AB = 10 - 6 = 4\)厘米。
线段的差
定义
如果一条线段可以看作是由一条较长的线段去掉其中一部分线段后剩余的部分,那么这条线段就是两条线段的差。
几何表示:如图,在线段\(AB\)上,点\(C\)在\(A\)、\(B\)之间,从线段\(AB\)中去掉线段\(AC\)后,剩余的线段\(CB\)就是\(AB\)与\(AC\)的差,即\(CB = AB - AC\)。
实例:一根长\(7\)厘米的线段,去掉其中\(3\)厘米长的一部分后,剩余部分的长度是\(7 - 3 = 4\)厘米,这\(4\)厘米的线段就是原来线段与去掉部分线段的差。
计算方法
已知两条线段的长度(较长线段和较短线段),求它们的差,用较长线段的长度减去较短线段的长度;若已知线段的差及其中一条线段的长度,求另一条线段的长度,根据差的关系进行计算。
例 1:已知线段\(AB = 8\)厘米,线段\(AC = 5\)厘米,点\(C\)在\(A\)、\(B\)之间,求\(BC\)的长度。
解:因为\(BC = AB - AC\),所以\(BC = 8 - 5 = 3\)厘米。
例 2:已知线段\(DE = 4\)厘米,\(DF - DE = 3\)厘米,且点\(E\)在\(D\)、\(F\)之间,求\(DF\)的长度。
解:因为\(DF - DE = 3\),所以\(DF = DE + 3 = 4 + 3 = 7\)厘米。
线段和差与中点的综合应用
当涉及线段中点时,可利用中点将线段分成相等的两部分的性质,结合线段的和差进行计算。
例 1:如图,点\(M\)是线段\(AB\)的中点,点\(N\)是线段\(BC\)的中点,\(AB = 6\)厘米,\(BC = 4\)厘米,求\(MN\)的长度。
解:因为点\(M\)是\(AB\)的中点,所以\(BM = \frac{1}{2}AB = \frac{1}{2} 6 = 3\)厘米。
因为点\(N\)是\(BC\)的中点,所以\(BN = \frac{1}{2}BC = \frac{1}{2} 4 = 2\)厘米。
又因为\(MN = BM + BN\),所以\(MN = 3 + 2 = 5\)厘米。
例 2:线段\(AC = 12\)厘米,点\(B\)是线段\(AC\)上一点,且\(AB = 5\)厘米,点\(D\)是线段\(AB\)的中点,点\(E\)是线段\(AC\)的中点,求\(DE\)的长度。
解:因为点\(E\)是\(AC\)的中点,所以\(AE = \frac{1}{2}AC = \frac{1}{2} 12 = 6\)厘米。
因为点\(D\)是\(AB\)的中点,所以\(AD = \frac{1}{2}AB = \frac{1}{2} 5 = 2.5\)厘米。
又因为\(DE = AE - AD\),所以\(DE = 6 - 2.5 = 3.5\)厘米。
复杂图形中线段和差的计算
在较复杂的图形中,需要先明确各线段之间的位置关系,找出已知线段和未知线段之间的和差关系,再进行计算。
例:如图,线段\(AB = 10\)厘米,点\(C\)在\(AB\)的延长线上,\(BC = 4\)厘米,点\(D\)在\(AB\)上,\(AD = 3\)厘米,求\(CD\)的长度。
解:由图可知,\(CD = DA + AB + BC\)(因为点\(C\)在\(AB\)延长线上,点\(D\)在\(AB\)上)。
代入数值可得:\(CD = 3 + 10 + 4 = 17\)厘米。
线段和差的应用
测量问题:在无法直接测量某条线段长度时,可通过测量与之相关的两条线段的长度,利用和差关系求出该线段的长度。例如,测量池塘两端的距离,可在池塘外选一点,测量这点到池塘两端的距离,再根据位置关系用和差计算。
工程建设:在道路施工中,已知两段道路的长度,可通过和差计算总长度;若已知总长度和其中一段的长度,可求出另一段的长度,以合理安排施工。
物品拼接:将几根短线段拼接成一根长线段,长线段的长度就是各短线段长度的和;将一根长线段截成几段,每段的长度可通过长线段与其他段长度的差求得。
课堂练习
已知线段\(AB = 7\)厘米,线段\(BC = 3\)厘米,点\(B\)在\(A\)、\(C\)之间,求\(AC\)的长度。
线段\(MN = 15\)厘米,线段\(MP = 9\)厘米,点\(P\)在\(M\)、\(N\)之间,求\(PN\)的长度。
点\(O\)是线段\(EF\)的中点,\(EG = 2\)厘米,\(GF = 6\)厘米,求\(EO\)的长度。
线段\(AB = 20\)厘米,点\(C\)在\(AB\)上,\(AC = 8\)厘米,点\(D\)是\(AC\)的中点,点\(E\)是\(CB\)的中点,求\(DE\)的长度。
总结
线段的和是指一条线段由另外两条线段首尾顺次连接组成,其长度为两条线段长度之和;线段的差是指一条线段由较长线段去掉一部分后剩余,其长度为较长线段与该部分线段长度之差。
计算线段和差时,要明确线段的位置关系,结合图形找出和差关系,若有中点,可利用中点性质将线段等分后再计算。
线段和差在实际测量、工程建设等领域有重要应用,掌握其计算方法有助于解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解线段的和差的意义,会用直尺和圆规作两条线段的
和与差,发展几何直观。
2.理解线段的中点的概念,会用刻度尺二等分线段。
3.会进行有关线段的和、差、倍、分的简单计算,发展
推理能力。
两条线段的和 两条线段的差(两条线段的和或
差仍是一条线段)
概念 如果一条线段的长度是 另两条线段的长度的 和,那么这条线段就叫 作另两条线段的和。 如果一条线段的长度是另两条线
段的长度的差,那么这条线段就
叫作另两条线段的差。
条件 ___________________________________________________________ 图形 _____________________________________________________ __________________________________
作法
结论
典例1 如图,已知线段, ,用直尺和圆
规作线段,使 。
解:如图所示,①作射线 ;
②用圆规在射线上连续截取 ;
③在线段上截取。线段 就是所求作的线段。
概念
几何表述
图示 ____________________________________________________
若点是线段的中点,则点一定在线段 上。
教材延伸
线段的三等分点、四等分点
将线段分成相等的三条线段,,,点,即线段 的
三等分点。同样还可以得到线段的四等分点等。如图所示。
类似地,还有线段的五等分点、六等分点等。
典例2 下列说法正确的是( )
D
A.若,则点为线段 的中点
B.若,则点为线段 的中点
C.若,则点为线段 的中点
D.若,则点为线段 的中点
解析:
选项 图示
A 不能 _____________________________________
选项 图示
B 不能
选项 图示
C 不能 _________________________________________
D 能 _________________________________
知识过关
①一般地,如果一条线段的长度是另两条线段的长度的和,那
么这条线段就叫作另 两条线段的和 ;如果一条线段的长
度是另两条线段的长度的差,那么这条线段就叫作另 两条
线段的差 .
②点C把线段AB分成相等的两条线段AC与BC,点C叫作线
段AB的 中点 .这时,AC= BC = AB ,AB
= 2AC = 2BC .
两条线段的和
两条
线段的差
中点
BC
AB
2AC
2BC
线段的和差
1. [2024·杭州余杭区期末]如图,下列关系式中与图不一定符
合的式子是( C )
A. AD-CD=AB+BC
B. AC-BC=AD-BD
C. AC-BC=BD-BC
D. AC-AB=BD-CD
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 线段AB的长为2 cm,延长AB到C,使AC=3AB,再延
长BA到D,使BD=2BC,则线段CD的长为( D )
A. 10 cm B. 8 cm
C. 6 cm D. 12 cm
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024·西安模拟]若点P在线段AB的延长线上,AP=8,
BP=3,则AB的长为 .
4. 已知点C,D在线段AB上,且AC=BD=1.5,若AB
=7,则CD的长为 .
5
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
尺规作图作线段的和差
5. 如图,已知线段a,b,画一条射线OM,在射线OM上
依次截取OA=AB=a,在线段BO上截取BC=b.则
( D )
A. OB=a+b B. OB=2b-a
C. OC=b-a D. OC=2a-b
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [母题 教材P175作业题T2]如图,已知线段a,b,用尺规
作一条线段c,使c=2a+b.(保留作图痕迹,不写作法)
【解】如答图所示:AE=2a+b=c.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
线段的中点
7. [2024·台州温岭期末]如图,M是线段AB的中点,N是线
段BM上一点,下列各式可以表示MN的长度的是
( B )
A. AB-BN B. AN-BM
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [母题 教材P174例2]如图,点M是AB的中点,点N是BD
的中点,AB=6 cm,BC=10 cm,CD=8 cm.则MN的
长为( A )
A. 12 cm B. 11 cm
C. 13 cm D. 10 cm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以BM=AM= AB= ×6=3(cm).
因为BC=10 cm,CD=8 cm,
所以BD=BC+CD=10+8=18(cm).
因为点N是BD的中点,
【点拨】
因为点M是AB的中点,AB=6 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以BN=DN= BD= ×18=9(cm),
所以MN=MB+BN=3+9=12(cm).
故选:A.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [2024·湖州期末]两根木条,一根长10 cm,另一根长12 cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为 cm.
11或1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [2024·绍兴诸暨期末]如图,M是线段AB的中点,点C
在线段AB上,N是线段AC的中点,且AN=2 cm,
CM=1 cm,求线段AB的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】因为N是线段AC的中点,且AN=2 cm,
所以NC=2 cm.
因为CM=1 cm,所以AM=5 cm.
因为M是线段AB的中点,
所以AB=2AM=10 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[易错题]点与线段的位置未分类讨论而出错
11. [2024·无锡期末]已知线段AB=7,点C为直线AB上一
点,且AC∶BC=4∶3,点D为线段AC的中点,则线段
BD的长为( C )
A. 5 B. 7
C. 5或7 D. 5.5或7
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [2024·菏泽期末]如图,C,D是线段AB上两点(点D
在点C右侧),E,F分别是线段AD,BC的中点.下列
结论:
①EF= AB;②若AE=BF,则AC=BD;③AB-
CD=2EF;④AC-BD=EC-DF. 其中正确的结论
是( B )
B
A. ①② B. ②③
C. ②④ D. ③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [新考向·知识情境化][2024·舟山调研] A,B,C三个住
宅区分别住有某公司职工30人、15人、10人,且这三个
住宅区在一条大道上(A,B,C三点共线),如图所示,
已知AB=100米,BC=200米,为了方便职工上下班,
该公司的接送车打算在此区间内设一个停靠点,为使所
有人步行到停靠点的路程之和最小,那么该停靠点的位
置应设在( A )
A
A. 点A B. 点B
C. 点A,B之间 D. 点B,C之间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. 如图,A,B,C,D是直线l上的四个点,M,N分
别是AB,CD的中点.
(1)如果MB=2 cm,NC=1.8 cm,BC=5 cm,则AD
的长为 cm;
12.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为MB=2 cm,NC=1.8 cm,
所以MB+NC=3.8 cm.
因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=
7.6 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以AD=AB+CD+BC=7.6+5=12.6(cm).
故答案为:12.6;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)如果MN=10 cm,BC=6 cm,则AD的长
为 cm;
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为MN=10 cm,BC=6 cm,
所以BM+CN=MN-BC=10-6=4(cm).
因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=8 cm,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以AD=AB+CD+BC=8+6=14(cm).
故答案为:14;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)如果MN=a,BC=b,求AD的长.
【解】因为MN=a,BC=b,所以BM+CN=a-b.因为M,N分别是AB,CD的中点,
所以AB=2BM,CD=2CN,
所以AB+CD=2BM+2CN=2(BM+CN)=2(a-
b),所以AD=AB+CD+BC=2(a-b)+b=2a-2b+b=2a-b.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. 已知线段AB,M,N分别是AC,BC的中点.
(1)如图,若点C在线段AB上,AC=12 cm,CB=9 cm,求线段MN的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】因为AC=12 cm,CB=9 cm,M,N分别是
AC,BC的中点,
所以CM= AC=6 cm,CN= BC=4.5 cm,
所以MN=CM+CN=6+4.5=10.5(cm);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若C为线段AB上任意一点,满足AC+CB=a cm,
你能猜出MN的长度吗?请说明理由.
【解】MN= cm,理由如下:
因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN=CM+CN= (AC+BC)= cm;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若点C在线段AB的延长线上,且满足AC-BC=
b cm,你能猜出MN的长度吗?请画出图形,写出你的
结论,并说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN=CM-CN= (AC-BC)= cm.
【解】如答图,MN= cm,理由如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
