1.6 利用三角函数测高 课件(共16张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 09:36:24 | ||
图片预览



文档简介
(共16张PPT)
6.利用三角函数测高
第一章 直角三角形的边角关系
议一议
教学过程
新课引入
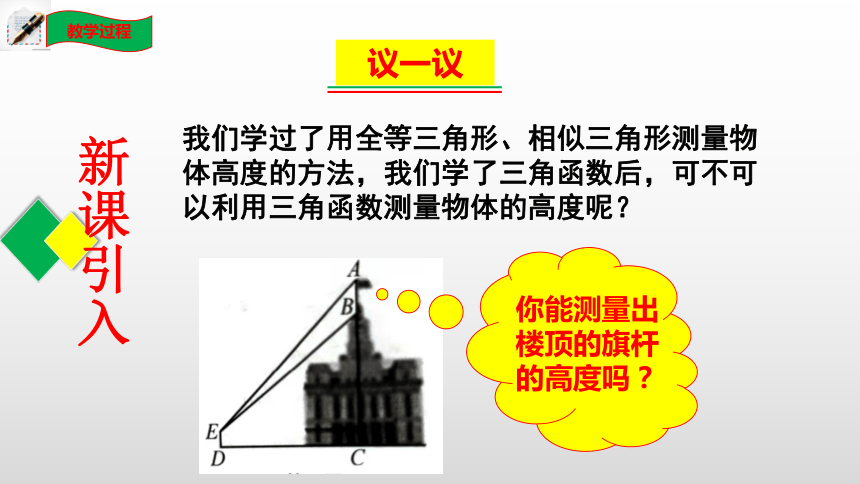
我们学过了用全等三角形、相似三角形测量物体高度的方法,我们学了三角函数后,可不可以利用三角函数测量物体的高度呢?
你能测量出楼顶的旗杆的高度吗?
议一议
教学过程
新知新授
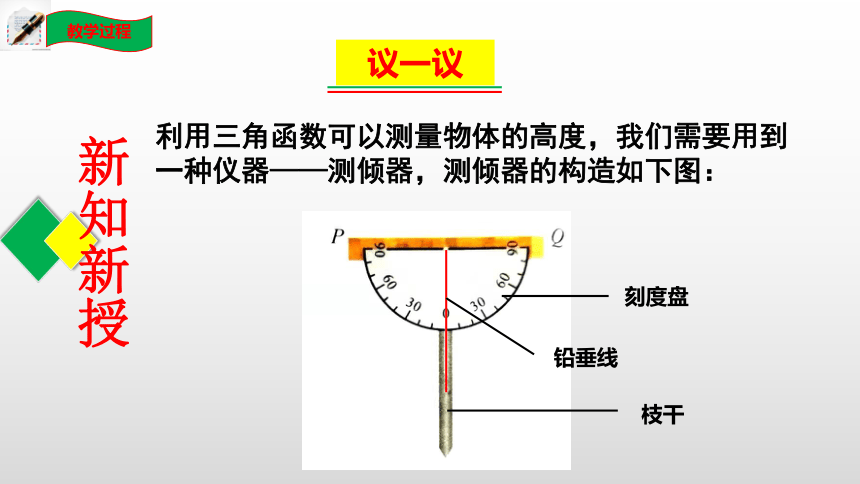
利用三角函数可以测量物体的高度,我们需要用到一种仪器——测倾器,测倾器的构造如下图:
刻度盘
铅垂线
枝干
做一做
教学过程
新知新授
活动一、用测倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数
做一做
教学过程
新知新授
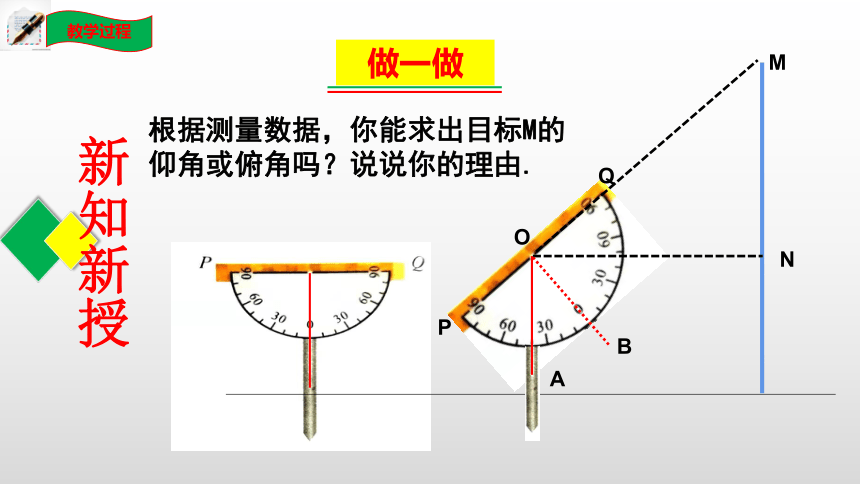
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
M
N
P
Q
O
A
B
做一做
教学过程
新知新授
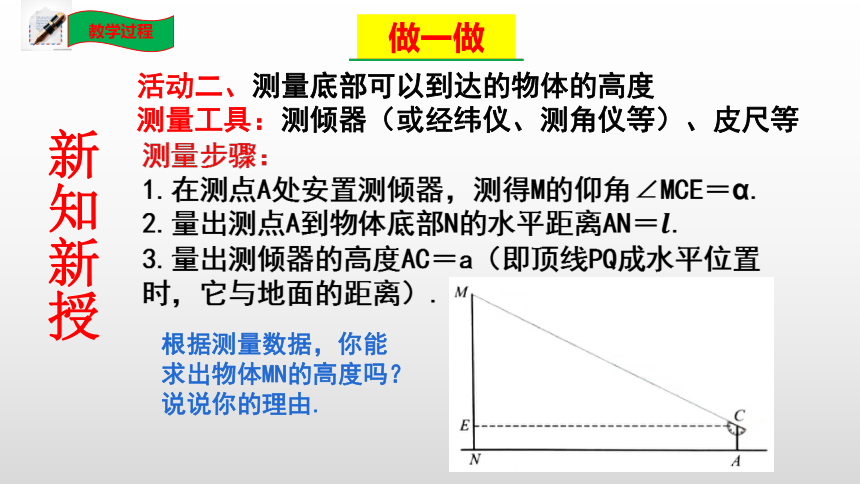
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
测量步骤:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
活动三、测量底部不可以到达的物体的高度
做一做
教学过程
新知新授
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
做一做
教学过程
例题解析
例1 如图,河对岸有一高层建筑物AB,为测其高,在C处由点D用测量仪测得顶端A的仰角为30°,向高层建筑物前进50 m,到达E处,由点F测得顶点A的仰角为45°,已知测量仪高CD=EF=1.2 m,求高层建筑物AB的高(结果精确到0.1 m).
做一做
教学过程
例题解析
例2.如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC.(结果取整数,参考数据:than48°≈1.11,tan58°≈1.60)
1.在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°(tan 27°≈0.51),此时旗杆在水平地面上的影子的长度为24 m,则旗杆的高度约为( )
A.24 m B.20 m C.16 m D.12 m
D
2.如图,小明在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD=10 m,楼高AB=24 m,则树高CD为____________ m.
A
4.如图,建筑物C上有一杆AB,从与BC相距10 m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为_____m.(结果取整数,参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
3
5.如图,AB是某景区内高10 m的观景台,CD是与AB底部相平的一座雕像(含底座),在观景台顶A处测得雕像顶C点的仰角为30°,从观景台底部B处向雕像方向水平前进6 m到达点E,在E处测得雕像顶C点的仰角为60°,已知雕像底座DF高8 m,求雕像CF的高.(结果保留根号)
6.如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量,先测得居民楼AB与CD之间的距离AC为35 m,后站在M点处测得居民楼CD的顶端D的仰角为45°,居民楼AB的顶端B的仰角为55°,已知居民楼CD的高度为16.6 m,小莹的观测点N距地面1.6 m.求居民楼AB的高度(精确到1m)(参考数据:sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43).
7.如图,学校教学楼上悬挂一块长为3 m的标语牌,即CD=3 m,数学活动课上,小明和小红要测量标语牌的底部D点到地面的距离.测量仪支架高AE=BF=1.2 m,小明在E处测得标语牌底部D点的仰角为31°,小红在F处测得标语牌顶部C点的仰角为45°,AB=5 m,依据他们测量的数据能否求出标语牌底部D点到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
教学过程
结束新课
感谢聆听
6.利用三角函数测高
第一章 直角三角形的边角关系
议一议
教学过程
新课引入
我们学过了用全等三角形、相似三角形测量物体高度的方法,我们学了三角函数后,可不可以利用三角函数测量物体的高度呢?
你能测量出楼顶的旗杆的高度吗?
议一议
教学过程
新知新授
利用三角函数可以测量物体的高度,我们需要用到一种仪器——测倾器,测倾器的构造如下图:
刻度盘
铅垂线
枝干
做一做
教学过程
新知新授
活动一、用测倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数
做一做
教学过程
新知新授
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
M
N
P
Q
O
A
B
做一做
教学过程
新知新授
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
测量步骤:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
活动三、测量底部不可以到达的物体的高度
做一做
教学过程
新知新授
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
做一做
教学过程
例题解析
例1 如图,河对岸有一高层建筑物AB,为测其高,在C处由点D用测量仪测得顶端A的仰角为30°,向高层建筑物前进50 m,到达E处,由点F测得顶点A的仰角为45°,已知测量仪高CD=EF=1.2 m,求高层建筑物AB的高(结果精确到0.1 m).
做一做
教学过程
例题解析
例2.如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC.(结果取整数,参考数据:than48°≈1.11,tan58°≈1.60)
1.在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°(tan 27°≈0.51),此时旗杆在水平地面上的影子的长度为24 m,则旗杆的高度约为( )
A.24 m B.20 m C.16 m D.12 m
D
2.如图,小明在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD=10 m,楼高AB=24 m,则树高CD为____________ m.
A
4.如图,建筑物C上有一杆AB,从与BC相距10 m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为_____m.(结果取整数,参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
3
5.如图,AB是某景区内高10 m的观景台,CD是与AB底部相平的一座雕像(含底座),在观景台顶A处测得雕像顶C点的仰角为30°,从观景台底部B处向雕像方向水平前进6 m到达点E,在E处测得雕像顶C点的仰角为60°,已知雕像底座DF高8 m,求雕像CF的高.(结果保留根号)
6.如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量,先测得居民楼AB与CD之间的距离AC为35 m,后站在M点处测得居民楼CD的顶端D的仰角为45°,居民楼AB的顶端B的仰角为55°,已知居民楼CD的高度为16.6 m,小莹的观测点N距地面1.6 m.求居民楼AB的高度(精确到1m)(参考数据:sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43).
7.如图,学校教学楼上悬挂一块长为3 m的标语牌,即CD=3 m,数学活动课上,小明和小红要测量标语牌的底部D点到地面的距离.测量仪支架高AE=BF=1.2 m,小明在E处测得标语牌底部D点的仰角为31°,小红在F处测得标语牌顶部C点的仰角为45°,AB=5 m,依据他们测量的数据能否求出标语牌底部D点到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
教学过程
结束新课
感谢聆听
