6.8 余角和补角 课件(共46张PPT)
文档属性
| 名称 | 6.8 余角和补角 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 09:11:41 | ||
图片预览











文档简介
(共46张PPT)
6.8 余角和补角
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
余角和补角
课程目标
理解余角和补角的定义,能准确判断两个角是否互为余角或补角。
掌握余角和补角的性质,并能运用这些性质解决角的计算问题。
明确余角和补角的区别与联系,提高对角的数量关系的理解和运用能力。
余角的定义
如果两个角的和等于\(90 °\)(直角),就说这两个角互为余角,简称互余。其中一个角是另一个角的余角。
几何表示:若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)与\(\angle 2\)互为余角,即\(\angle 1\)是\(\angle 2\)的余角,\(\angle 2\)也是\(\angle 1\)的余角。
实例:\(\angle 3 = 30 °\),\(\angle 4 = 60 °\),因为\(30 ° + 60 ° = 90 °\),所以\(\angle 3\)与\(\angle 4\)互为余角。
注意:互为余角的两个角只与它们的度数之和有关,与它们的位置无关。即无论两个角的位置如何,只要它们的和是\(90 °\),就互为余角。
补角的定义
如果两个角的和等于\(180 °\)(平角),就说这两个角互为补角,简称互补。其中一个角是另一个角的补角。
几何表示:若\(\angle \alpha + \angle \beta = 180 °\),则\(\angle \alpha\)与\(\angle \beta\)互为补角,即\(\angle \alpha\)是\(\angle \beta\)的补角,\(\angle \beta\)也是\(\angle \alpha\)的补角。
实例:\(\angle 5 = 110 °\),\(\angle 6 = 70 °\),因为\(110 ° + 70 ° = 180 °\),所以\(\angle 5\)与\(\angle 6\)互为补角。
注意:与余角类似,互为补角的两个角也只与度数之和有关,与位置无关。
余角和补角的性质
余角的性质:同角(或等角)的余角相等。
几何表示:
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 1 + \angle 3 = 90 °\),则\(\angle 2 = \angle 3\)(同角的余角相等)。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 3 + \angle 4 = 90 °\),且\(\angle 1 = \angle 3\),则\(\angle 2 = \angle 4\)(等角的余角相等)。
实例:已知\(\angle A = 30 °\),\(\angle B\)和\(\angle C\)都是\(\angle A\)的余角,则\(\angle B = \angle C = 60 °\)。
补角的性质:同角(或等角)的补角相等。
几何表示:
若\(\angle \alpha + \angle \beta = 180 °\),\(\angle \alpha + \angle \gamma = 180 °\),则\(\angle \beta = \angle \gamma\)(同角的补角相等)。
若\(\angle \alpha + \angle \beta = 180 °\),\(\angle \gamma + \angle \delta = 180 °\),且\(\angle \alpha = \angle \gamma\),则\(\angle \beta = \angle \delta\)(等角的补角相等)。
实例:已知\(\angle M = 120 °\),\(\angle N\)和\(\angle P\)都是\(\angle M\)的补角,则\(\angle N = \angle P = 60 °\)。
余角和补角的计算
求一个角的余角
若已知一个角的度数为\(x\),则它的余角的度数为\(90 ° - x\)(其中\(0 ° < x < 90 °\),因为只有锐角才有余角)。
例 1:求\(50 °\)角的余角。
解:\(90 ° - 50 ° = 40 °\),所以\(50 °\)角的余角是\(40 °\)。
例 2:一个角的余角是\(35 °\),求这个角的度数。
解:设这个角的度数为\(x\),则\(x + 35 ° = 90 °\),解得\(x = 90 ° - 35 ° = 55 °\)。
求一个角的补角
若已知一个角的度数为\(y\),则它的补角的度数为\(180 ° - y\)(其中\(0 ° < y < 180 °\),除平角外,其他角都有补角)。
例 3:求\(100 °\)角的补角。
解:\(180 ° - 100 ° = 80 °\),所以\(100 °\)角的补角是\(80 °\)。
例 4:一个角的补角是\(70 °\),求这个角的度数。
解:设这个角的度数为\(y\),则\(y + 70 ° = 180 °\),解得\(y = 180 ° - 70 ° = 110 °\)。
余角和补角的区别与联系
区别
度数和不同:互为余角的两个角的和是\(90 °\);互为补角的两个角的和是\(180 °\)。
存在范围不同:只有锐角(小于\(90 °\)的角)才有余角;除平角(\(180 °\))外,锐角、直角、钝角都有补角(直角的补角是直角,钝角的补角是锐角)。
联系
都是针对两个角而言的,体现的是两个角之间的数量关系,与位置无关。
若一个角有补角和余角,则它的补角比它的余角大\(90 °\)。即若一个角为\(x\),则其补角为\(180 ° - x\),余角为\(90 ° - x\),补角与余角的差为\((180 ° - x) - (90 ° - x) = 90 °\)。
生活中的余角和补角
余角和补角在生活中也有一定的应用:
墙角的两边形成直角(\(90 °\)),如果在墙角处放置一个梯子,梯子与其中一边形成的角和梯子与另一边形成的角互为余角。
一条直线可以看作是一个平角(\(180 °\)),在直线上取一点,过该点作一条射线,射线与直线的两边形成的两个角互为补角。
易错点提醒
互为余角和互为补角的两个角只与度数和有关,与它们的位置没有关系,不要误认为必须有公共顶点或公共边。
不要混淆余角和补角的度数和,余角是和为\(90 °\),补角是和为\(180 °\)。
只有锐角才有余角,直角和钝角没有余角;平角没有补角。
课堂练习
判断下列说法是否正确:
若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)是余角。
一个角的补角一定是钝角。
同角的补角相等。
求下列角的余角和补角:
\(30 °\)
\(65 °\)
\(90 °\)(思考:它有余角吗?)
一个角的补角是它的 3 倍,求这个角的度数。
已知\(\angle A\)与\(\angle B\)互为余角,\(\angle A = 25 °\),求\(\angle B\)的补角的度数。
总结
余角是指两个角的和为\(90 °\),补角是指两个角的和为\(180 °\),它们都体现两个角的数量关系。
余角和补角的性质:同角(或等角)的余角相等,同角(或等角)的补角相等。
计算一个角的余角用\(90 °\)减去这个角的度数,计算补角用\(180 °\)减去这个角的度数,同时要注意它们的区别和存在范围。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解互为余角、互为补角的概念,会求一个角的余角
或补角。
2.掌握同角或等角的余角(补角)相等,并能说明两角
相等,培养推理能力。
3.会用方向角表示方向,发展几何直观。
名称 概念 数学语言 图示
互为 余角 如果两个锐角的和是一 个直角,我们就说这两 个角互为余角,简称互 余,也可以说其中一个 角是另一个角的余角。 ____________________________
名称 概念 数学语言 图示
互为 补角 如果两个角的和是一个 平角,我们就说这两个 角互为补角,简称互 补,也可以说其中一个 角是另一个角的补角。 __________________________________
(1)两个角互余或互补是两个角之间的数量
关系,与它们的位置无关。(2)若两个角互余,则这
两个角一定都是锐角;若两个角互补,则这两个角可能
都是直角,也可能一个是锐角,另一个是钝角。
典例1 (1)若一个角是 ,则它的余角是____,它的
补角是______,它的补角比它的余角大____。
解析:一个角是 ,它的余角是 ,
它的补角是 ,它的补角比它的余角
大 。(一个锐角的补角始终比其余角
大 ,与该锐角的度数无关)
(2)若一个角的余角是 ,则这个角是_______,
这个角的补角是________。
解析:一个角的余角是,
这个角是 ,
这个角的补角是 。
1.余角的性质:同角或等角的余角相等。
2.补角的性质:同角或等角的补角相等。
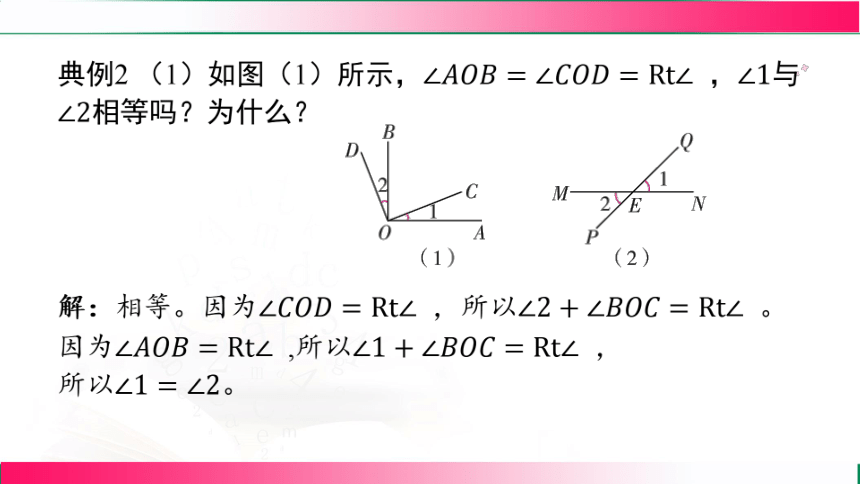
典例2 (1)如图(1)所示, , 与
相等吗?为什么?
解:相等。因为 ,所以 。
因为 ,所以 ,
所以 。
(2)如图(2)所示,直线与直线相交于点, 与
相等吗?为什么?
解:相等。因为点,,在同一条直线上,
所以 ,即 。
因为点,,在同一条直线上,所以 ,
即 ,
所以 。
1.方向角:一般地,方向角是以第一个方向
(正南或正北)为角的始边向第二个方向
(东或西)转动所形成的角。如图,射线
的方向是北偏东 ,射线 的方向是南偏西
。
2.特殊角的表示:东北方向表示北偏东 ,西北方向表示
北偏西 ,东南方向表示南偏东 ,西南方向表示南偏西 。
方向角通常先写北或南,再写偏东或偏西,如“北偏东
”一般不写成“东偏北 ”。
典例3 (绍兴柯桥区期末)如图,甲从点 出发沿
北偏东 方向走到点,乙从点 出发沿南偏
西 方向走到点,则 的度数是( )
D
A. B. C. D.
解析:由题意知, ,
,
所以 。
知识过关
①如果两个锐角的和是一个直角,我们就说这两个角 互
余 ;如果两个角的和是一个 平角 ,我们就说这两个角
互为补角.
② 同角或等角 的余角相等、补角相等.
互
余
平角
同角或等角
余角、补角的概念
1. 将一副三角板按如图所示的位置摆放,其中∠α与∠β一定
互余的是( C )
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 若∠A的补角是120°50',则∠A的余角的度数是( B )
A. 30°10' B. 30°50'
C. 59°10' D. 59°50'
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024·桐庐期末]如图,AB⊥AC,AD⊥BC,垂足分别
为A,D,图中互余的角共有( C )
A. 2对 B. 3对
C. 4对 D. 5对
(第3题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. 如图,∠AOB=∠COD=∠EOF=90°,则∠1,
∠2,∠3之间的数量关系为( D )
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
(第4题)
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5. 已知∠α=29°45'38″,则∠α的补角的度数
是 .
6. 如图,PA,PB表示以P为起点的两条公路,其中公路
PA的走向是南偏西34°,公路PB与正南方向夹角的余角
是30°,则这两条公路的夹角∠APB= °.
150°14'22″
94
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024·东莞期末]已知一个角的补角比这个角的余角的2倍
还多30°.
(1)设这个角的度数为x,则它的补角为 ;
它的余角为 ;(用x表示)
(2)求这个角的度数.
【解】由题意可知,(180°-x)-2(90°-x)=
30°,解得x=30°.
即这个角的度数是30°.
180°-x
90°-x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
余角、补角的性质
8. 如图,点O在直线AB上,∠COB=∠EOD=90°,下
列说法错误的是( D )
A. ∠1=∠2
B. ∠AOE与∠2互余
C. ∠AOD与∠1互补
D. ∠AOD与∠COD互补
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为∠COB=∠EOD=90°,
所以∠1+∠COD=∠2+∠COD=90°,
所以∠1=∠2,故A选项正确;
因为∠AOE+∠1=90°,
所以∠AOE+∠2=90°,即∠AOE与∠2互余,故
B选项正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为∠AOD+∠2=180°,
所以∠AOD+∠1=180°,即∠AOD与∠1互补,
故C选项正确;
无法判断∠AOD与∠COD是否互补,D选项错误.
故选D.
D
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 已知∠1+∠2=180°,∠2+∠3=180°,则下列说法一
定正确的是( A )
A. ∠1=∠3 B. ∠2=∠3
C. ∠1=∠2 D. ∠1=∠2=∠3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [2024·金华东阳期末]如图,一副三角板按不同的位置摆
放,摆放位置中∠α=∠β的图形有 .(填序号)
②③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
根据直角三角板中每个角的度数,可以判断出图①
中∠α=45°,∠β=60°;图②中∠α=∠β=45°;由
同角的余角相等可得图③中∠α=∠β,由等角的补角相
等可得图④中∠α=∠β,在图⑤中∠α+∠β=180°,
不相等,因此摆放位置中∠α=∠β的图形有②③④.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11. ∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式
子有:①90°-∠β;②∠α-90°;③ (∠α+∠β);
④ (∠α-∠β),其中错误的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以∠β=180°-∠α,∠α=180°-∠β.
因为90°-∠β+∠β=90°,所以90°-∠β为∠β
的余角.
因为∠α-90°=180°-∠β-90°=90°-∠β,
所以∠α-90°为∠β的余角.
【点拨】
因为∠α和∠β互补,且∠α>∠β,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为 (∠α+∠β)=90°,所以它不是∠β的余角.
因为 (∠α-∠β)= (180°-∠β-∠β)=90°-
∠β,所以 (∠α-∠β)为∠β的余角.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [2024·杭州拱墅区期末]已知∠γ是∠α的补角,∠β是∠γ
的补角,若∠α=(2n-30)°,∠β=(60-n)°,则∠γ
的度数为 .
【点拨】
因为∠γ是∠α的补角,∠β是∠γ的补角,所以易得
∠α=∠β,
所以(2n-30)°=(60-n)°,
所以n=30,所以∠α=30°,
所以∠γ=180°-30°=150°.
150°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [新视角·新定义题]我们定义:有一条公共边的两个互余
的角为“友余角”,现在∠α和∠β为一对“友余角”,
∠α=20°,则∠α和∠β的平分线所成角的度数
为 .
【点拨】
因为∠α和∠β为一对“友余角”,∠α=20°,所
以∠β=70°,所以∠α和∠β的平分线所成角的度数为
∠α+ ∠β=45°或 ∠β- ∠α=25°.
45°或25°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. 如图,射线OA的方向是北偏东15°,射线OB的方向是
北偏西40°,∠AOB=∠AOC,射线OD是OB的反向
延长线.
(1)射线OC的方向是 ;
北偏东70°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为射线OB的方向是北偏西40°,射线OA的方
向是北偏东15°,
所以∠NOB=40°,∠NOA=15°,
【点拨】
如图,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以∠AOB=∠NOB+∠NOA=55°.
因为∠AOB=∠AOC,
所以∠AOC=55°,
所以∠NOC=∠NOA+∠AOC=70°,
所以射线OC的方向是北偏东70°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】由题意,知∠AOB=55°,∠AOC=
∠AOB,所以∠AOC=55°,
所以∠BOC=110°.
又因为射线OD是OB的反向延长线,
所以∠BOD=180°,
所以∠COD=180°-110°=70°.
又因为射线OE平分∠COD,
所以∠COE=35°.
所以∠AOE=∠AOC+∠COE=90°.
(2)若射线OE平分∠COD,求∠AOE的度数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)直接写出一对互余的角是 ,一
对互补的角是 . (答案不唯一)
∠AOC与∠COE
∠AOB与∠AOD
(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新视角·操作探究题](1)如图①,将两块直角三角板的直
角顶点C叠放在一起.
①若∠DCE=40°,则∠ACB的度数是多少?若
∠ACB=120°,则∠DCE的度数是多少?
②猜想∠ACB与∠DCE的度数有何特殊关系,并说明
理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】①因为∠ACD=90°,∠DCE=40°,
所以∠ACE=∠ACD-∠DCE=90°-40°=50°.
又因为∠BCE=90°,
所以∠ACB=50°+90°=140°.
因为∠BCE=90°,∠ACB=120°,
所以∠ACE=∠ACB-∠BCE=120°-90°=30°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
又因为∠ACD=90°,
所以∠DCE=90°-30°=60°.
②∠ACB+∠DCE=180°.理由:因为∠ACB=
∠ACD+∠BCD=90°+∠BCD,
所以∠ACB+∠DCE=90°+∠BCD+∠DCE=
90°+∠BCE=180°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)如图②,若是两块同样的三角板60°锐角的顶点A叠
放在一起,则∠DAB与∠CAE的度数有何关系?请
说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】∠DAB+∠CAE=120°.理由:
因为∠DAB=∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB+∠CAE=
60°+∠EAB=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)如图③,已知∠AOB=α,作∠COD=β(α,β都是锐
角且α>β),若OC在∠AOB的内部,请直接写出
∠AOD与∠BOC的度数关系,不必说明理由.
【解】∠AOD+∠BOC=α-β或∠AOD+∠BOC
=α+β或∠BOC-∠AOD=α-β.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
6.8 余角和补角
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
余角和补角
课程目标
理解余角和补角的定义,能准确判断两个角是否互为余角或补角。
掌握余角和补角的性质,并能运用这些性质解决角的计算问题。
明确余角和补角的区别与联系,提高对角的数量关系的理解和运用能力。
余角的定义
如果两个角的和等于\(90 °\)(直角),就说这两个角互为余角,简称互余。其中一个角是另一个角的余角。
几何表示:若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)与\(\angle 2\)互为余角,即\(\angle 1\)是\(\angle 2\)的余角,\(\angle 2\)也是\(\angle 1\)的余角。
实例:\(\angle 3 = 30 °\),\(\angle 4 = 60 °\),因为\(30 ° + 60 ° = 90 °\),所以\(\angle 3\)与\(\angle 4\)互为余角。
注意:互为余角的两个角只与它们的度数之和有关,与它们的位置无关。即无论两个角的位置如何,只要它们的和是\(90 °\),就互为余角。
补角的定义
如果两个角的和等于\(180 °\)(平角),就说这两个角互为补角,简称互补。其中一个角是另一个角的补角。
几何表示:若\(\angle \alpha + \angle \beta = 180 °\),则\(\angle \alpha\)与\(\angle \beta\)互为补角,即\(\angle \alpha\)是\(\angle \beta\)的补角,\(\angle \beta\)也是\(\angle \alpha\)的补角。
实例:\(\angle 5 = 110 °\),\(\angle 6 = 70 °\),因为\(110 ° + 70 ° = 180 °\),所以\(\angle 5\)与\(\angle 6\)互为补角。
注意:与余角类似,互为补角的两个角也只与度数之和有关,与位置无关。
余角和补角的性质
余角的性质:同角(或等角)的余角相等。
几何表示:
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 1 + \angle 3 = 90 °\),则\(\angle 2 = \angle 3\)(同角的余角相等)。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 3 + \angle 4 = 90 °\),且\(\angle 1 = \angle 3\),则\(\angle 2 = \angle 4\)(等角的余角相等)。
实例:已知\(\angle A = 30 °\),\(\angle B\)和\(\angle C\)都是\(\angle A\)的余角,则\(\angle B = \angle C = 60 °\)。
补角的性质:同角(或等角)的补角相等。
几何表示:
若\(\angle \alpha + \angle \beta = 180 °\),\(\angle \alpha + \angle \gamma = 180 °\),则\(\angle \beta = \angle \gamma\)(同角的补角相等)。
若\(\angle \alpha + \angle \beta = 180 °\),\(\angle \gamma + \angle \delta = 180 °\),且\(\angle \alpha = \angle \gamma\),则\(\angle \beta = \angle \delta\)(等角的补角相等)。
实例:已知\(\angle M = 120 °\),\(\angle N\)和\(\angle P\)都是\(\angle M\)的补角,则\(\angle N = \angle P = 60 °\)。
余角和补角的计算
求一个角的余角
若已知一个角的度数为\(x\),则它的余角的度数为\(90 ° - x\)(其中\(0 ° < x < 90 °\),因为只有锐角才有余角)。
例 1:求\(50 °\)角的余角。
解:\(90 ° - 50 ° = 40 °\),所以\(50 °\)角的余角是\(40 °\)。
例 2:一个角的余角是\(35 °\),求这个角的度数。
解:设这个角的度数为\(x\),则\(x + 35 ° = 90 °\),解得\(x = 90 ° - 35 ° = 55 °\)。
求一个角的补角
若已知一个角的度数为\(y\),则它的补角的度数为\(180 ° - y\)(其中\(0 ° < y < 180 °\),除平角外,其他角都有补角)。
例 3:求\(100 °\)角的补角。
解:\(180 ° - 100 ° = 80 °\),所以\(100 °\)角的补角是\(80 °\)。
例 4:一个角的补角是\(70 °\),求这个角的度数。
解:设这个角的度数为\(y\),则\(y + 70 ° = 180 °\),解得\(y = 180 ° - 70 ° = 110 °\)。
余角和补角的区别与联系
区别
度数和不同:互为余角的两个角的和是\(90 °\);互为补角的两个角的和是\(180 °\)。
存在范围不同:只有锐角(小于\(90 °\)的角)才有余角;除平角(\(180 °\))外,锐角、直角、钝角都有补角(直角的补角是直角,钝角的补角是锐角)。
联系
都是针对两个角而言的,体现的是两个角之间的数量关系,与位置无关。
若一个角有补角和余角,则它的补角比它的余角大\(90 °\)。即若一个角为\(x\),则其补角为\(180 ° - x\),余角为\(90 ° - x\),补角与余角的差为\((180 ° - x) - (90 ° - x) = 90 °\)。
生活中的余角和补角
余角和补角在生活中也有一定的应用:
墙角的两边形成直角(\(90 °\)),如果在墙角处放置一个梯子,梯子与其中一边形成的角和梯子与另一边形成的角互为余角。
一条直线可以看作是一个平角(\(180 °\)),在直线上取一点,过该点作一条射线,射线与直线的两边形成的两个角互为补角。
易错点提醒
互为余角和互为补角的两个角只与度数和有关,与它们的位置没有关系,不要误认为必须有公共顶点或公共边。
不要混淆余角和补角的度数和,余角是和为\(90 °\),补角是和为\(180 °\)。
只有锐角才有余角,直角和钝角没有余角;平角没有补角。
课堂练习
判断下列说法是否正确:
若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)是余角。
一个角的补角一定是钝角。
同角的补角相等。
求下列角的余角和补角:
\(30 °\)
\(65 °\)
\(90 °\)(思考:它有余角吗?)
一个角的补角是它的 3 倍,求这个角的度数。
已知\(\angle A\)与\(\angle B\)互为余角,\(\angle A = 25 °\),求\(\angle B\)的补角的度数。
总结
余角是指两个角的和为\(90 °\),补角是指两个角的和为\(180 °\),它们都体现两个角的数量关系。
余角和补角的性质:同角(或等角)的余角相等,同角(或等角)的补角相等。
计算一个角的余角用\(90 °\)减去这个角的度数,计算补角用\(180 °\)减去这个角的度数,同时要注意它们的区别和存在范围。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解互为余角、互为补角的概念,会求一个角的余角
或补角。
2.掌握同角或等角的余角(补角)相等,并能说明两角
相等,培养推理能力。
3.会用方向角表示方向,发展几何直观。
名称 概念 数学语言 图示
互为 余角 如果两个锐角的和是一 个直角,我们就说这两 个角互为余角,简称互 余,也可以说其中一个 角是另一个角的余角。 ____________________________
名称 概念 数学语言 图示
互为 补角 如果两个角的和是一个 平角,我们就说这两个 角互为补角,简称互 补,也可以说其中一个 角是另一个角的补角。 __________________________________
(1)两个角互余或互补是两个角之间的数量
关系,与它们的位置无关。(2)若两个角互余,则这
两个角一定都是锐角;若两个角互补,则这两个角可能
都是直角,也可能一个是锐角,另一个是钝角。
典例1 (1)若一个角是 ,则它的余角是____,它的
补角是______,它的补角比它的余角大____。
解析:一个角是 ,它的余角是 ,
它的补角是 ,它的补角比它的余角
大 。(一个锐角的补角始终比其余角
大 ,与该锐角的度数无关)
(2)若一个角的余角是 ,则这个角是_______,
这个角的补角是________。
解析:一个角的余角是,
这个角是 ,
这个角的补角是 。
1.余角的性质:同角或等角的余角相等。
2.补角的性质:同角或等角的补角相等。
典例2 (1)如图(1)所示, , 与
相等吗?为什么?
解:相等。因为 ,所以 。
因为 ,所以 ,
所以 。
(2)如图(2)所示,直线与直线相交于点, 与
相等吗?为什么?
解:相等。因为点,,在同一条直线上,
所以 ,即 。
因为点,,在同一条直线上,所以 ,
即 ,
所以 。
1.方向角:一般地,方向角是以第一个方向
(正南或正北)为角的始边向第二个方向
(东或西)转动所形成的角。如图,射线
的方向是北偏东 ,射线 的方向是南偏西
。
2.特殊角的表示:东北方向表示北偏东 ,西北方向表示
北偏西 ,东南方向表示南偏东 ,西南方向表示南偏西 。
方向角通常先写北或南,再写偏东或偏西,如“北偏东
”一般不写成“东偏北 ”。
典例3 (绍兴柯桥区期末)如图,甲从点 出发沿
北偏东 方向走到点,乙从点 出发沿南偏
西 方向走到点,则 的度数是( )
D
A. B. C. D.
解析:由题意知, ,
,
所以 。
知识过关
①如果两个锐角的和是一个直角,我们就说这两个角 互
余 ;如果两个角的和是一个 平角 ,我们就说这两个角
互为补角.
② 同角或等角 的余角相等、补角相等.
互
余
平角
同角或等角
余角、补角的概念
1. 将一副三角板按如图所示的位置摆放,其中∠α与∠β一定
互余的是( C )
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 若∠A的补角是120°50',则∠A的余角的度数是( B )
A. 30°10' B. 30°50'
C. 59°10' D. 59°50'
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [2024·桐庐期末]如图,AB⊥AC,AD⊥BC,垂足分别
为A,D,图中互余的角共有( C )
A. 2对 B. 3对
C. 4对 D. 5对
(第3题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. 如图,∠AOB=∠COD=∠EOF=90°,则∠1,
∠2,∠3之间的数量关系为( D )
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
(第4题)
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5. 已知∠α=29°45'38″,则∠α的补角的度数
是 .
6. 如图,PA,PB表示以P为起点的两条公路,其中公路
PA的走向是南偏西34°,公路PB与正南方向夹角的余角
是30°,则这两条公路的夹角∠APB= °.
150°14'22″
94
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024·东莞期末]已知一个角的补角比这个角的余角的2倍
还多30°.
(1)设这个角的度数为x,则它的补角为 ;
它的余角为 ;(用x表示)
(2)求这个角的度数.
【解】由题意可知,(180°-x)-2(90°-x)=
30°,解得x=30°.
即这个角的度数是30°.
180°-x
90°-x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
余角、补角的性质
8. 如图,点O在直线AB上,∠COB=∠EOD=90°,下
列说法错误的是( D )
A. ∠1=∠2
B. ∠AOE与∠2互余
C. ∠AOD与∠1互补
D. ∠AOD与∠COD互补
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
因为∠COB=∠EOD=90°,
所以∠1+∠COD=∠2+∠COD=90°,
所以∠1=∠2,故A选项正确;
因为∠AOE+∠1=90°,
所以∠AOE+∠2=90°,即∠AOE与∠2互余,故
B选项正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为∠AOD+∠2=180°,
所以∠AOD+∠1=180°,即∠AOD与∠1互补,
故C选项正确;
无法判断∠AOD与∠COD是否互补,D选项错误.
故选D.
D
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 已知∠1+∠2=180°,∠2+∠3=180°,则下列说法一
定正确的是( A )
A. ∠1=∠3 B. ∠2=∠3
C. ∠1=∠2 D. ∠1=∠2=∠3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [2024·金华东阳期末]如图,一副三角板按不同的位置摆
放,摆放位置中∠α=∠β的图形有 .(填序号)
②③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【点拨】
根据直角三角板中每个角的度数,可以判断出图①
中∠α=45°,∠β=60°;图②中∠α=∠β=45°;由
同角的余角相等可得图③中∠α=∠β,由等角的补角相
等可得图④中∠α=∠β,在图⑤中∠α+∠β=180°,
不相等,因此摆放位置中∠α=∠β的图形有②③④.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11. ∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式
子有:①90°-∠β;②∠α-90°;③ (∠α+∠β);
④ (∠α-∠β),其中错误的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以∠β=180°-∠α,∠α=180°-∠β.
因为90°-∠β+∠β=90°,所以90°-∠β为∠β
的余角.
因为∠α-90°=180°-∠β-90°=90°-∠β,
所以∠α-90°为∠β的余角.
【点拨】
因为∠α和∠β互补,且∠α>∠β,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为 (∠α+∠β)=90°,所以它不是∠β的余角.
因为 (∠α-∠β)= (180°-∠β-∠β)=90°-
∠β,所以 (∠α-∠β)为∠β的余角.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [2024·杭州拱墅区期末]已知∠γ是∠α的补角,∠β是∠γ
的补角,若∠α=(2n-30)°,∠β=(60-n)°,则∠γ
的度数为 .
【点拨】
因为∠γ是∠α的补角,∠β是∠γ的补角,所以易得
∠α=∠β,
所以(2n-30)°=(60-n)°,
所以n=30,所以∠α=30°,
所以∠γ=180°-30°=150°.
150°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [新视角·新定义题]我们定义:有一条公共边的两个互余
的角为“友余角”,现在∠α和∠β为一对“友余角”,
∠α=20°,则∠α和∠β的平分线所成角的度数
为 .
【点拨】
因为∠α和∠β为一对“友余角”,∠α=20°,所
以∠β=70°,所以∠α和∠β的平分线所成角的度数为
∠α+ ∠β=45°或 ∠β- ∠α=25°.
45°或25°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. 如图,射线OA的方向是北偏东15°,射线OB的方向是
北偏西40°,∠AOB=∠AOC,射线OD是OB的反向
延长线.
(1)射线OC的方向是 ;
北偏东70°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为射线OB的方向是北偏西40°,射线OA的方
向是北偏东15°,
所以∠NOB=40°,∠NOA=15°,
【点拨】
如图,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
所以∠AOB=∠NOB+∠NOA=55°.
因为∠AOB=∠AOC,
所以∠AOC=55°,
所以∠NOC=∠NOA+∠AOC=70°,
所以射线OC的方向是北偏东70°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】由题意,知∠AOB=55°,∠AOC=
∠AOB,所以∠AOC=55°,
所以∠BOC=110°.
又因为射线OD是OB的反向延长线,
所以∠BOD=180°,
所以∠COD=180°-110°=70°.
又因为射线OE平分∠COD,
所以∠COE=35°.
所以∠AOE=∠AOC+∠COE=90°.
(2)若射线OE平分∠COD,求∠AOE的度数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)直接写出一对互余的角是 ,一
对互补的角是 . (答案不唯一)
∠AOC与∠COE
∠AOB与∠AOD
(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新视角·操作探究题](1)如图①,将两块直角三角板的直
角顶点C叠放在一起.
①若∠DCE=40°,则∠ACB的度数是多少?若
∠ACB=120°,则∠DCE的度数是多少?
②猜想∠ACB与∠DCE的度数有何特殊关系,并说明
理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】①因为∠ACD=90°,∠DCE=40°,
所以∠ACE=∠ACD-∠DCE=90°-40°=50°.
又因为∠BCE=90°,
所以∠ACB=50°+90°=140°.
因为∠BCE=90°,∠ACB=120°,
所以∠ACE=∠ACB-∠BCE=120°-90°=30°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
又因为∠ACD=90°,
所以∠DCE=90°-30°=60°.
②∠ACB+∠DCE=180°.理由:因为∠ACB=
∠ACD+∠BCD=90°+∠BCD,
所以∠ACB+∠DCE=90°+∠BCD+∠DCE=
90°+∠BCE=180°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)如图②,若是两块同样的三角板60°锐角的顶点A叠
放在一起,则∠DAB与∠CAE的度数有何关系?请
说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】∠DAB+∠CAE=120°.理由:
因为∠DAB=∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB+∠CAE=
60°+∠EAB=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)如图③,已知∠AOB=α,作∠COD=β(α,β都是锐
角且α>β),若OC在∠AOB的内部,请直接写出
∠AOD与∠BOC的度数关系,不必说明理由.
【解】∠AOD+∠BOC=α-β或∠AOD+∠BOC
=α+β或∠BOC-∠AOD=α-β.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
