2024-2025学年山东省泰安市宁阳县宁阳三中八年级(下)第一次月考数学试卷(五四学制)(无答案)
文档属性
| 名称 | 2024-2025学年山东省泰安市宁阳县宁阳三中八年级(下)第一次月考数学试卷(五四学制)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 19:42:20 | ||
图片预览

文档简介
2024-2025学年山东省泰安市宁阳三中八年级(下)第一次月考数学试卷(五四学制)
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式是最简二次根式的是( )
A. B. C. D.
2.下列式子正确的是( )
A. B. C. D.
3.式子在实数范围内有意义,则x的取值范围是( )
A. x≠1 B. x≥-2且x≠1 C. x≠-2 D. x>-2且x≠1
4.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
A. 4 B. 6 C. 8 D. 10
5.设x、y为实数,且,则|x-y|的值是( )
A. 1 B. 5 C. 2 D. 0
6.如图,直线L上有三个正方形a,b,c,若正方形a的边长为1,正方形c的边长为3,则正方形b的面积为( )
A. 4 B. 9 C. 10 D. 11
7.若1≤a≤2,则化简+|a-2|的结果是( )
A. 2a-3 B. 3-2a C. -2a D. 1
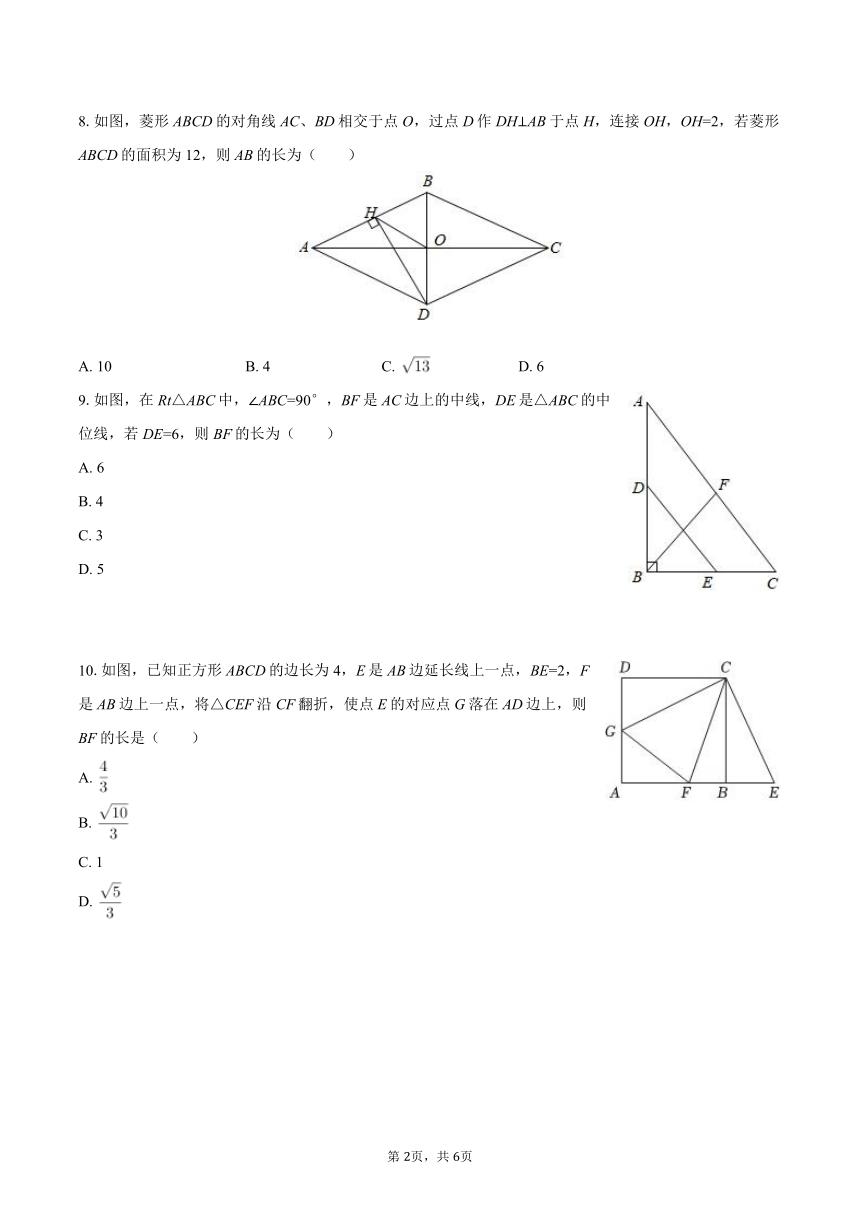
8.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=2,若菱形ABCD的面积为12,则AB的长为( )
A. 10 B. 4 C. D. 6
9.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=6,则BF的长为( )
A. 6
B. 4
C. 3
D. 5
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,则BF的长是( )
A.
B.
C. 1
D.
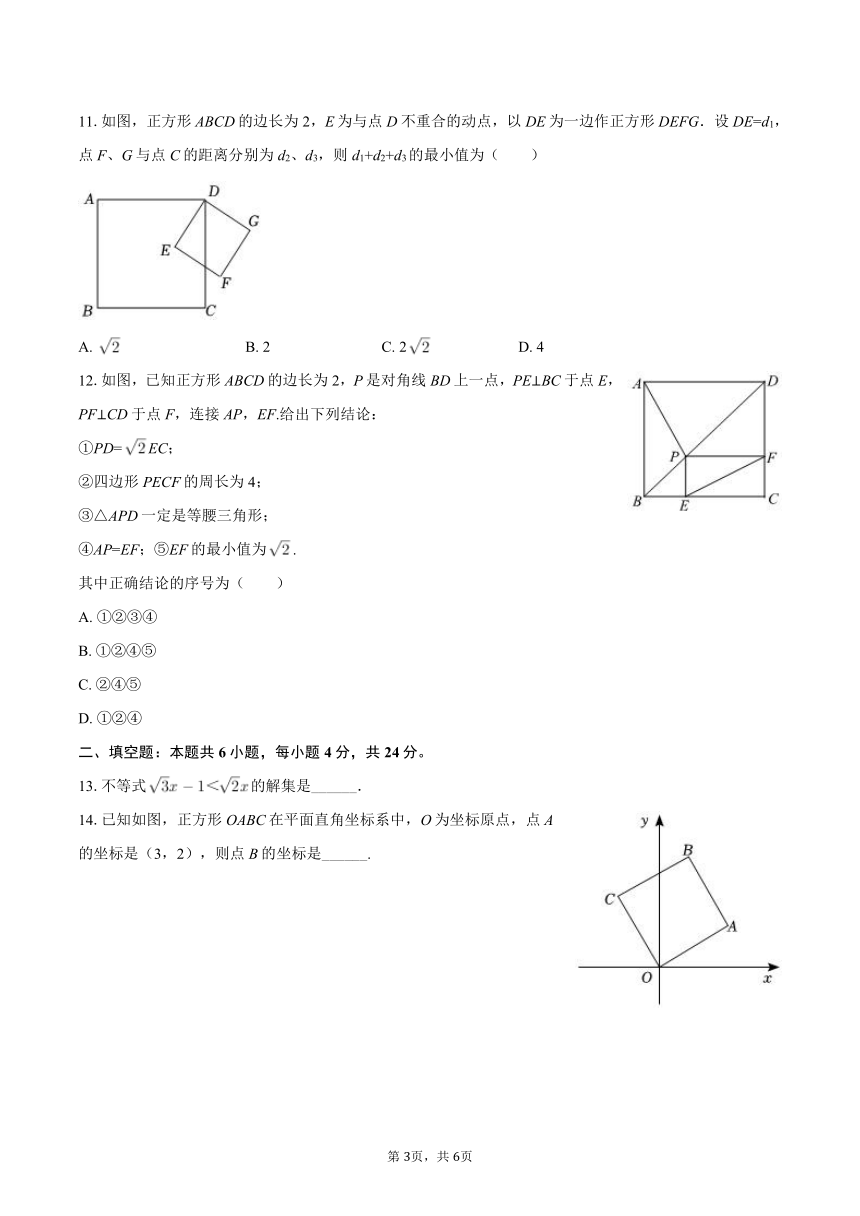
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B. 2 C. 2 D. 4
12.如图,已知正方形ABCD的边长为2,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:
①PD=EC;
②四边形PECF的周长为4;
③△APD一定是等腰三角形;
④AP=EF;⑤EF的最小值为.
其中正确结论的序号为( )
A. ①②③④
B. ①②④⑤
C. ②④⑤
D. ①②④
二、填空题:本题共6小题,每小题4分,共24分。
13.不等式的解集是______.
14.已知如图,正方形OABC在平面直角坐标系中,O为坐标原点,点A的坐标是(3,2),则点B的坐标是______.
15.如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG,若AF=3,DG=4,FG=5,矩形ABCD的面积为______.
16.如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是____.
17.如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连DF,∠CDF等于______°.
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题40分)
二次根式的计算:
(1);
(2)2;
(3);
(4);
(5);
(6);
(7)(6)();
(8);
(9)-()×()2;
(10)()-(3).
20.(本小题8分)
如图,在 ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
21.(本小题8分)
如图1,Rt△CEF中,∠C=90°,∠CEF,∠CFE的外角平分线交于点A,过点A作AB⊥CE的延长线于B,过点A作AD⊥CF的延长线于D.求证:四边形ABCD是正方形.
22.(本小题10分)
如图,四边形ABCD为平行四边形,对角线AC的垂直平分线EF分别交边AD,BC于点E,F,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)在BC的延长线上取一点G,使CG=OC,连接OG.若F为BC的中点,且∠G=15°,AB=8,求△FOG的面积.
23.(本小题12分)
如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
第1页,共1页
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式是最简二次根式的是( )
A. B. C. D.
2.下列式子正确的是( )
A. B. C. D.
3.式子在实数范围内有意义,则x的取值范围是( )
A. x≠1 B. x≥-2且x≠1 C. x≠-2 D. x>-2且x≠1
4.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
A. 4 B. 6 C. 8 D. 10
5.设x、y为实数,且,则|x-y|的值是( )
A. 1 B. 5 C. 2 D. 0
6.如图,直线L上有三个正方形a,b,c,若正方形a的边长为1,正方形c的边长为3,则正方形b的面积为( )
A. 4 B. 9 C. 10 D. 11
7.若1≤a≤2,则化简+|a-2|的结果是( )
A. 2a-3 B. 3-2a C. -2a D. 1
8.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=2,若菱形ABCD的面积为12,则AB的长为( )
A. 10 B. 4 C. D. 6
9.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=6,则BF的长为( )
A. 6
B. 4
C. 3
D. 5
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,则BF的长是( )
A.
B.
C. 1
D.
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B. 2 C. 2 D. 4
12.如图,已知正方形ABCD的边长为2,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:
①PD=EC;
②四边形PECF的周长为4;
③△APD一定是等腰三角形;
④AP=EF;⑤EF的最小值为.
其中正确结论的序号为( )
A. ①②③④
B. ①②④⑤
C. ②④⑤
D. ①②④
二、填空题:本题共6小题,每小题4分,共24分。
13.不等式的解集是______.
14.已知如图,正方形OABC在平面直角坐标系中,O为坐标原点,点A的坐标是(3,2),则点B的坐标是______.
15.如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG,若AF=3,DG=4,FG=5,矩形ABCD的面积为______.
16.如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是____.
17.如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连DF,∠CDF等于______°.
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题40分)
二次根式的计算:
(1);
(2)2;
(3);
(4);
(5);
(6);
(7)(6)();
(8);
(9)-()×()2;
(10)()-(3).
20.(本小题8分)
如图,在 ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
21.(本小题8分)
如图1,Rt△CEF中,∠C=90°,∠CEF,∠CFE的外角平分线交于点A,过点A作AB⊥CE的延长线于B,过点A作AD⊥CF的延长线于D.求证:四边形ABCD是正方形.
22.(本小题10分)
如图,四边形ABCD为平行四边形,对角线AC的垂直平分线EF分别交边AD,BC于点E,F,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)在BC的延长线上取一点G,使CG=OC,连接OG.若F为BC的中点,且∠G=15°,AB=8,求△FOG的面积.
23.(本小题12分)
如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
第1页,共1页
同课章节目录
