2024-2025学年云南省曲靖市第一中学高一下学期期中测试数学试题B(含答案)
文档属性
| 名称 | 2024-2025学年云南省曲靖市第一中学高一下学期期中测试数学试题B(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 456.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 21:42:43 | ||
图片预览




文档简介
2024-2025学年云南省曲靖市第一中学高一下学期期中测试数学试题B
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.集合,则( )
A. B.
C. D.
2.已知复数,则( )
A. 1 B. 2 C. D.
3.在中,角、、的对边分别为、、.若,则的大小不可能为( )
A. B. C. D.
4.一个平面图形用斜二测画法画出的直观图如图所示,O'A'B'是等腰直角三角形且O'A'=A'B',其中斜边O'B'=,则这个平面图形的面积是( )
A. 3 B. C. D.
5.已知单位向量的夹角为,则与的夹角为( )
A. B. C. D.
6.已知x1,f(x)=x,g(x)=1-,h(x)=(x-)三个函数图象如图所示,则f(x),g(x),h(x)的图象依次为图中的()
A. ,, B. ,, C. ,, D. ,,
7.在中,角A,B,C的对边分别为a,b,c.已知,,,点O是的外心,若,则( )
A. B. C. D.
8.已知函数为偶函数,则的值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知复数,则( )
A. B. C. D. 的虚部为1
10.已知向量,,则( )
A. 当时,
B. 当时,
C. 当时,在方向上的投影向量为
D. 当与夹角为锐角时,
11.在中,内角A,B,C,的对边分别是a,b,c,,且,则下列结论正确的是( )
A. B. 外接圆的面积为
C. 的面积的最大值为 D. 的最大值是8
三、填空题:本题共3小题,每小题5分,共15分。
12.若一个球的半径是1,则这个球的表面积是 .
13.已知方程的两虚根为、,若,则实数的值为
14.已知,若满足(互不相等),则的取值范围是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知点O(0,0),向量=(2,3),=(4,-3),=(1,).
(1)若,求的值;
(2)若点P在线段AB的延长线上,且||=||,求点P的坐标.
16.(本小题12分)
在ABC中,角A,B,C的对边分别是a,b,c,且2a(C+)=b+c.
(1)求A;
(2)如果a=2且ABC的面积为,求角B的大小.
17.(本小题12分)
已知圆锥的顶点为,母线,所成角的余弦值为,轴截面等腰三角形的顶角为,若的面积为.
(1)求该圆锥的侧面积;
(2)求该圆锥的内接圆柱侧面积的最大值;
(3)求圆锥的内切球体积.
18.(本小题12分)
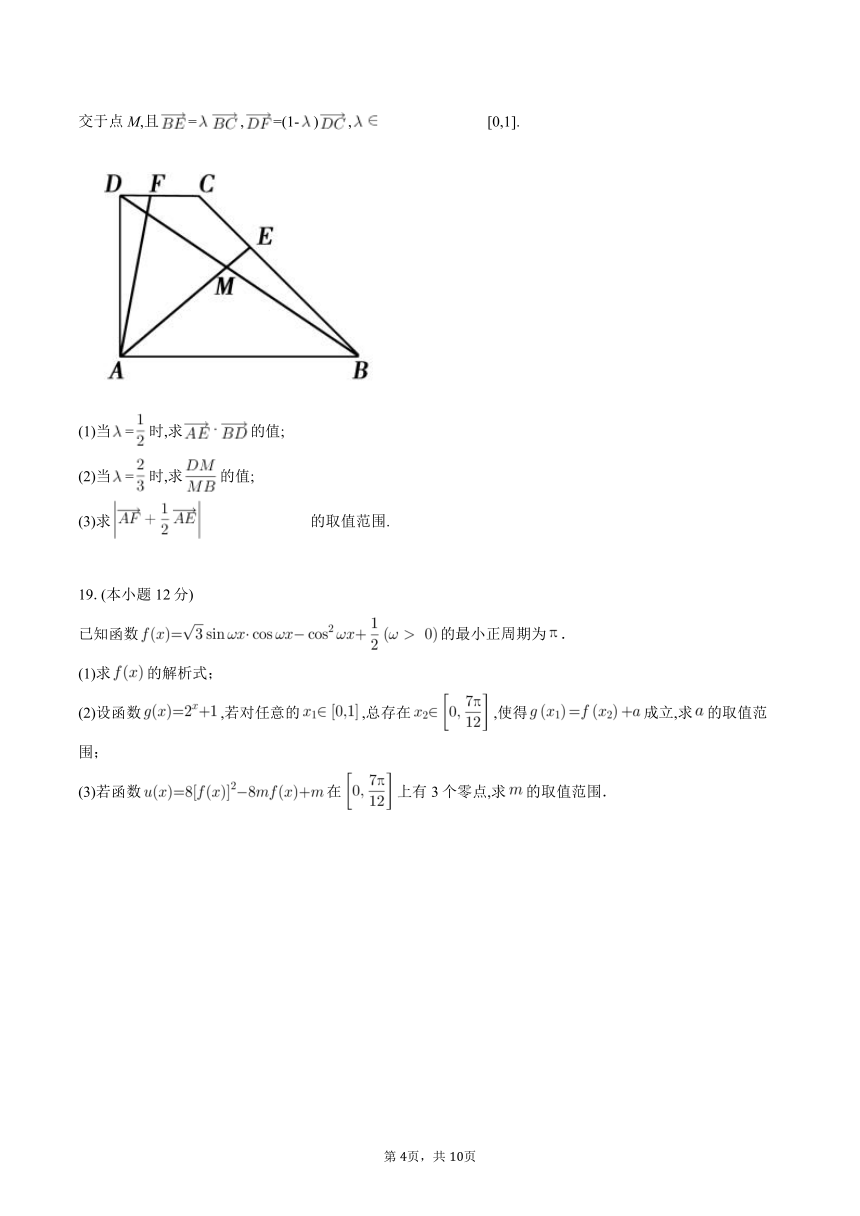
在直角梯形ABCD中,已知ABDC,ADAB,CD=1,AD=2,AB=3,动点E、F分别在线段BC和DC上,AE和BD交于点M,且=,=(1-), [0,1].
(1)当=时,求的值;
(2)当=时,求的值;
(3)求 的取值范围.
19.(本小题12分)
已知函数的最小正周期为.
(1)求的解析式;
(2)设函数,若对任意的,总存在,使得成立,求的取值范围;
(3)若函数在上有3个零点,求的取值范围.
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】ACD
10.【答案】AC
11.【答案】ACD
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:(1)=-=(2,-6),
因为,
所以=2-6=0,得=;
(2) 设P(x,y),
因为点P在线段AB的延长线上且||=||,
所以=,
所以,
解得:,
所以点P的坐标为(8,-15).
16.【答案】解:(1)因为2a(C+)=b+c,
所以aC+aC=b+c,
由正弦定理,得
AC+AC=B+C
=(A+C)+C=AC+AC+C
所以AC=AC+C,
因为C0,
所以1=A-A=2(A-),
即(A-)=,
因为,
所以-< A-<,
所以A-=,即A=;
(2)根据正弦定理,===,
所以ABC的面积为:
S=bcA=BC
=BC=B(-B)
=(2B-)+,
由(2B-)+=可得(2B-)=,
因为,
所以-<2B-<,
所以2B-=或2B-=,
所以B=或B=.
17.【答案】(1)设圆锥母线长、底面半径分别为、,
由圆锥的轴截面为等腰三角形且顶角为,则,解得,
又,所以,
又因为的面积为,
∴,解得(负值舍去),
又,所以,
∴圆锥的侧面积.
(2)作出轴截面如下所示:
设圆柱底面半径,即,
由(1)可知,则,又圆锥的高,
所以,即圆柱的高为,
所以圆锥内接圆柱的侧面积,
当且仅当,即时取等号,
所以圆锥内接圆柱的侧面积的最大值为.
(3)作出轴截面如图所示:
根据圆锥的性质可知内切球球心在上,设球心为,切于点,
设内切球半径为,即,则,
所以,
由(1)可知,圆锥的高,,
则有,解得,
所以圆锥的内切球的体积.
18.【答案】解:(1)=+=+
=+(++)
=-++
=(1-)+,
当=时,=+,
又=-,ADAB,
=(+)(-)
=-+
=-6+2=-4;
(2)当时,,
设,,
得,
,
,不共线,,
解得,即;
(3)因为,
,
所以,
又ADAB,
所以
=5-6+,
由题意知,,
所以,当时,取到最小值,
当时, 取到最大值,
故的取值范围是.
19.【答案】解:(1)因为
,
因为函数的最小正周期为,且,
则,所以,
所以;
(2)因为是增函数,则当时,,
当时,,则,
所以,
由题意可知,
则,解得,
即的取值范围为;
(3)令,
由(2)知当时,,即,
则函数有两个零点,
且的图象与直线,共有3个公共点,
由的图象可知,当,时,
,得,
由,得,,符合题意,
当,时,
得,解得,
综上,的取值范围为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.集合,则( )
A. B.
C. D.
2.已知复数,则( )
A. 1 B. 2 C. D.
3.在中,角、、的对边分别为、、.若,则的大小不可能为( )
A. B. C. D.
4.一个平面图形用斜二测画法画出的直观图如图所示,O'A'B'是等腰直角三角形且O'A'=A'B',其中斜边O'B'=,则这个平面图形的面积是( )
A. 3 B. C. D.
5.已知单位向量的夹角为,则与的夹角为( )
A. B. C. D.
6.已知x1,f(x)=x,g(x)=1-,h(x)=(x-)三个函数图象如图所示,则f(x),g(x),h(x)的图象依次为图中的()
A. ,, B. ,, C. ,, D. ,,
7.在中,角A,B,C的对边分别为a,b,c.已知,,,点O是的外心,若,则( )
A. B. C. D.
8.已知函数为偶函数,则的值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知复数,则( )
A. B. C. D. 的虚部为1
10.已知向量,,则( )
A. 当时,
B. 当时,
C. 当时,在方向上的投影向量为
D. 当与夹角为锐角时,
11.在中,内角A,B,C,的对边分别是a,b,c,,且,则下列结论正确的是( )
A. B. 外接圆的面积为
C. 的面积的最大值为 D. 的最大值是8
三、填空题:本题共3小题,每小题5分,共15分。
12.若一个球的半径是1,则这个球的表面积是 .
13.已知方程的两虚根为、,若,则实数的值为
14.已知,若满足(互不相等),则的取值范围是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知点O(0,0),向量=(2,3),=(4,-3),=(1,).
(1)若,求的值;
(2)若点P在线段AB的延长线上,且||=||,求点P的坐标.
16.(本小题12分)
在ABC中,角A,B,C的对边分别是a,b,c,且2a(C+)=b+c.
(1)求A;
(2)如果a=2且ABC的面积为,求角B的大小.
17.(本小题12分)
已知圆锥的顶点为,母线,所成角的余弦值为,轴截面等腰三角形的顶角为,若的面积为.
(1)求该圆锥的侧面积;
(2)求该圆锥的内接圆柱侧面积的最大值;
(3)求圆锥的内切球体积.
18.(本小题12分)
在直角梯形ABCD中,已知ABDC,ADAB,CD=1,AD=2,AB=3,动点E、F分别在线段BC和DC上,AE和BD交于点M,且=,=(1-), [0,1].
(1)当=时,求的值;
(2)当=时,求的值;
(3)求 的取值范围.
19.(本小题12分)
已知函数的最小正周期为.
(1)求的解析式;
(2)设函数,若对任意的,总存在,使得成立,求的取值范围;
(3)若函数在上有3个零点,求的取值范围.
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】ACD
10.【答案】AC
11.【答案】ACD
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:(1)=-=(2,-6),
因为,
所以=2-6=0,得=;
(2) 设P(x,y),
因为点P在线段AB的延长线上且||=||,
所以=,
所以,
解得:,
所以点P的坐标为(8,-15).
16.【答案】解:(1)因为2a(C+)=b+c,
所以aC+aC=b+c,
由正弦定理,得
AC+AC=B+C
=(A+C)+C=AC+AC+C
所以AC=AC+C,
因为C0,
所以1=A-A=2(A-),
即(A-)=,
因为,
所以-< A-<,
所以A-=,即A=;
(2)根据正弦定理,===,
所以ABC的面积为:
S=bcA=BC
=BC=B(-B)
=(2B-)+,
由(2B-)+=可得(2B-)=,
因为,
所以-<2B-<,
所以2B-=或2B-=,
所以B=或B=.
17.【答案】(1)设圆锥母线长、底面半径分别为、,
由圆锥的轴截面为等腰三角形且顶角为,则,解得,
又,所以,
又因为的面积为,
∴,解得(负值舍去),
又,所以,
∴圆锥的侧面积.
(2)作出轴截面如下所示:
设圆柱底面半径,即,
由(1)可知,则,又圆锥的高,
所以,即圆柱的高为,
所以圆锥内接圆柱的侧面积,
当且仅当,即时取等号,
所以圆锥内接圆柱的侧面积的最大值为.
(3)作出轴截面如图所示:
根据圆锥的性质可知内切球球心在上,设球心为,切于点,
设内切球半径为,即,则,
所以,
由(1)可知,圆锥的高,,
则有,解得,
所以圆锥的内切球的体积.
18.【答案】解:(1)=+=+
=+(++)
=-++
=(1-)+,
当=时,=+,
又=-,ADAB,
=(+)(-)
=-+
=-6+2=-4;
(2)当时,,
设,,
得,
,
,不共线,,
解得,即;
(3)因为,
,
所以,
又ADAB,
所以
=5-6+,
由题意知,,
所以,当时,取到最小值,
当时, 取到最大值,
故的取值范围是.
19.【答案】解:(1)因为
,
因为函数的最小正周期为,且,
则,所以,
所以;
(2)因为是增函数,则当时,,
当时,,则,
所以,
由题意可知,
则,解得,
即的取值范围为;
(3)令,
由(2)知当时,,即,
则函数有两个零点,
且的图象与直线,共有3个公共点,
由的图象可知,当,时,
,得,
由,得,,符合题意,
当,时,
得,解得,
综上,的取值范围为.
第1页,共1页
同课章节目录
