1.2.4 绝对值 课件(共16张PPT)
文档属性
| 名称 | 1.2.4 绝对值 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 542.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 16:14:25 | ||
图片预览




文档简介
(共16张PPT)
第 一章 有理数
1.2 有理数及其大小比较
1.2.4 绝对值
初中数学七年级上册(RJ版)
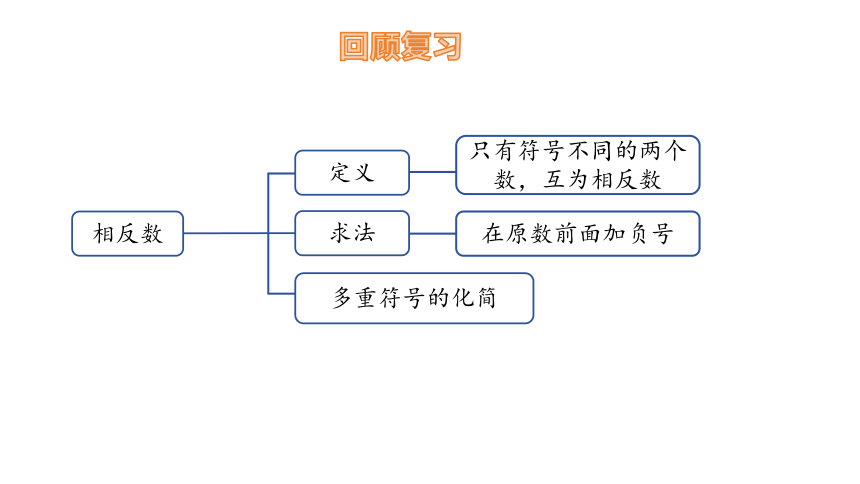
回顾复习
相反数
定义
求法
多重符号的化简
在原数前面加负号
只有符号不同的两个数,互为相反数
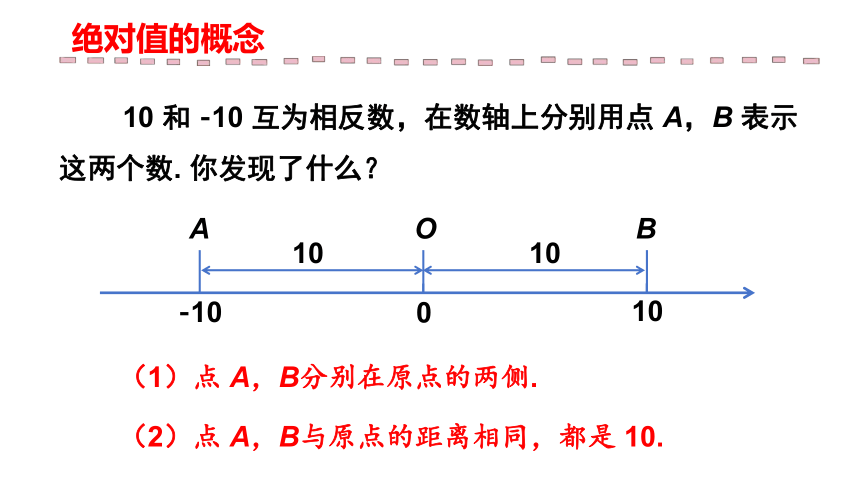
10 和 -10 互为相反数,在数轴上分别用点 A,B 表示这两个数. 你发现了什么?
0
10
-10
10
10
A
B
O
(1)点 A,B分别在原点的两侧.
(2)点 A,B与原点的距离相同,都是 10.
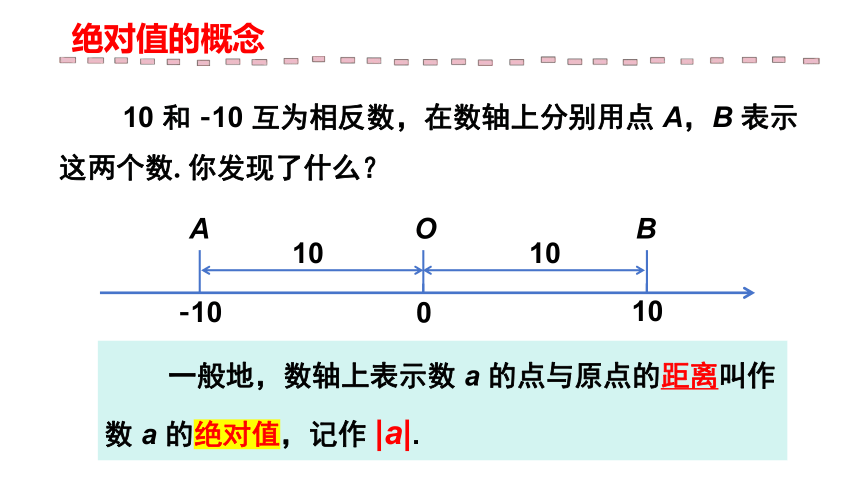
绝对值的概念
10 和 -10 互为相反数,在数轴上分别用点 A,B 表示这两个数. 你发现了什么?
0
10
-10
10
10
A
B
O
一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作 |a|.
绝对值的概念
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
习题巩固
5
3.5
3
4.5
0
思考: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
结论1:一个正数的绝对值是正数.
一个负数的绝对值是正数.
0的绝对值是0.
结论2:一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a= 0 时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗
| 0.2 |=
| b |= (b<0)
智力大比拼:
| a – b | = (a>b)
| a – b | = (a<b)
绝对值的性质
问:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
|-5|=5
|+5|=5
互为相反数,符号相反
绝对值相等
因为距离不可能是负数,所以一个数的绝对值不会是负数。
即 | a | ≥ 0.
非负性
绝对值的性质
追问:讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
例 (1)分别写出 1, -0.5 和 的绝对值;
| 1 | = 1;
0
1
2
-1
-2
距离为1
距离为0.5
距离为
|-0.5| = 0.5;
典例解析
(2)因为在点 A,B,C,D 中,点 C 离原点最近,所以在有理数 a,b,c,d 中,c 的绝对值最小.
(2)如图,数轴上的点 A,B,C,D 分别表示有理数a,b,c,d,这四个数中,绝对值最小的是哪个数?
0
1
2
3
-1
-2
-3
4
-4
A
B
C
D
分析:对于(2),一个数的绝对值越小,数轴上表示它的点离原点越近;反过来,数轴上的点离原点越近,它所表示的数的绝对值越小.
随堂练习
1.
C
2.
A
3.下列说法中,正确的是( )
A.|-8|是求-8的相反数
B.|-8|表示的意义是数轴上表示-8的点到原点的距离
C.|-8|表示的意义是数轴上表示-8的点到原点的距离是-8
D.以上都不对
B
拓展提升
2.下列各式中无论m为何值,一定是正数的是 ( )
A. 0 B. -1 C. +1 D.-(-m)
1.
C
C
1.一般地,数轴上表示数a的点与原点的距离,叫作数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
归纳小结
提起绝对值的产生,就需要从“现代分析学之父”的德国大数学家魏尔斯特拉斯(Weierstrass,1815-1897)说起,他于1841年提出绝对值的定义,距今不到200年的历史。绝对值在数学的世界里看似简单却又充满深意的概念。它如同一面镜子,映照出数轴上数字的真实面貌。。
第 一章 有理数
1.2 有理数及其大小比较
1.2.4 绝对值
初中数学七年级上册(RJ版)
回顾复习
相反数
定义
求法
多重符号的化简
在原数前面加负号
只有符号不同的两个数,互为相反数
10 和 -10 互为相反数,在数轴上分别用点 A,B 表示这两个数. 你发现了什么?
0
10
-10
10
10
A
B
O
(1)点 A,B分别在原点的两侧.
(2)点 A,B与原点的距离相同,都是 10.
绝对值的概念
10 和 -10 互为相反数,在数轴上分别用点 A,B 表示这两个数. 你发现了什么?
0
10
-10
10
10
A
B
O
一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作 |a|.
绝对值的概念
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
习题巩固
5
3.5
3
4.5
0
思考: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
结论1:一个正数的绝对值是正数.
一个负数的绝对值是正数.
0的绝对值是0.
结论2:一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a= 0 时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗
| 0.2 |=
| b |= (b<0)
智力大比拼:
| a – b | = (a>b)
| a – b | = (a<b)
绝对值的性质
问:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
|-5|=5
|+5|=5
互为相反数,符号相反
绝对值相等
因为距离不可能是负数,所以一个数的绝对值不会是负数。
即 | a | ≥ 0.
非负性
绝对值的性质
追问:讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
例 (1)分别写出 1, -0.5 和 的绝对值;
| 1 | = 1;
0
1
2
-1
-2
距离为1
距离为0.5
距离为
|-0.5| = 0.5;
典例解析
(2)因为在点 A,B,C,D 中,点 C 离原点最近,所以在有理数 a,b,c,d 中,c 的绝对值最小.
(2)如图,数轴上的点 A,B,C,D 分别表示有理数a,b,c,d,这四个数中,绝对值最小的是哪个数?
0
1
2
3
-1
-2
-3
4
-4
A
B
C
D
分析:对于(2),一个数的绝对值越小,数轴上表示它的点离原点越近;反过来,数轴上的点离原点越近,它所表示的数的绝对值越小.
随堂练习
1.
C
2.
A
3.下列说法中,正确的是( )
A.|-8|是求-8的相反数
B.|-8|表示的意义是数轴上表示-8的点到原点的距离
C.|-8|表示的意义是数轴上表示-8的点到原点的距离是-8
D.以上都不对
B
拓展提升
2.下列各式中无论m为何值,一定是正数的是 ( )
A. 0 B. -1 C. +1 D.-(-m)
1.
C
C
1.一般地,数轴上表示数a的点与原点的距离,叫作数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
归纳小结
提起绝对值的产生,就需要从“现代分析学之父”的德国大数学家魏尔斯特拉斯(Weierstrass,1815-1897)说起,他于1841年提出绝对值的定义,距今不到200年的历史。绝对值在数学的世界里看似简单却又充满深意的概念。它如同一面镜子,映照出数轴上数字的真实面貌。。
同课章节目录
