新高考高三数学函数的图象一轮复习课件(共64张PPT)
文档属性
| 名称 | 新高考高三数学函数的图象一轮复习课件(共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 11:01:17 | ||
图片预览











文档简介
(共64张PPT)
基础知识及典例
新高考数学一轮复习
函数的图象
01
考情透视·目标导航
考点要求 考题统计 考情分析
(1)函数图像的识别 (2)函数图像的应用 (3)函数图像的变换 2024年全国甲卷第7题,5分 2024年I卷第7题,5分 2023年天津卷第4题,5分 2022年天津卷第3题,5分 2022年全国乙卷第8题,5分 2022年全国甲卷第5题,5分 基本初等函数的图像是高考中的重要考点之一,是研究函数性质的重要工具.高考中总以一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等的图像为基础来考查函数图像,往往结合函数性质一并考查,考查的内容主要有知式选图、知图选式、图像变换以及灵活地应用图像判断方程解的个数,属于每年必考内容之一.
复习目标: (1)在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数. (2)会画简单的函数图象. (3)会运用函数图象研究函数的性质,解决方程解的个数与不等式解的问题.
02
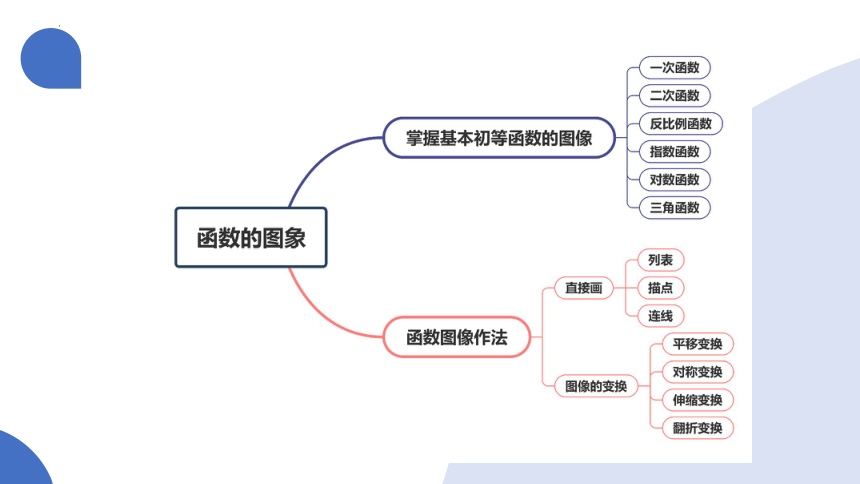
知识导图·思维引航
02
03
考点突破·题型探究
(1)一次函数;
(2)二次函数;
(3)反比例函数;
(4)指数函数;
(5)对数函数;
(6)三角函数.
知识梳理·基础回归
知识点1:掌握基本初等函数的图像
1、直接画
①确定定义域;②化简解析式;③考察性质:奇偶性(或其他对称性)、单调性、周期性、凹凸性;④特殊点、极值点、与横/纵坐标交点;⑤特殊线(对称轴、渐近线等).
知识梳理·基础回归
知识点2:函数图像作法
2、图像的变换
(1)平移变换
①函数的图像是把函数的图像沿轴向左平移个单位得到的;
②函数的图像是把函数的图像沿轴向右平移个单位得到的;
③函数的图像是把函数的图像沿轴向上平移个单位得到的;
④函数的图像是把函数的图像沿轴向下平移个单位得到的;
知识梳理·基础回归
(2)对称变换
-f(x)
f(-x)
-f(-x)
logax(a>0,且a≠1)
知识梳理·基础回归
(3)翻折变换
|f(x)|
f(|x|)
知识梳理·基础回归
(4)伸缩变换
①的图像,可将的图像上的每一点的纵坐标伸长或缩短到原来的倍得到.
②的图像,可将的图像上的每一点的横坐标伸长或缩短到原来的倍得到.
知识梳理·基础回归
解题方法总结
(1)若恒成立,则的图像关于直线对称.
(2)设函数定义在实数集上,则函数与的图象关于直线对称.
(3)若,对任意恒成立,则的图象关于直线对称.
(4)函数与函数的图象关于直线对称.
(5)函数与函数的图象关于直线对称.
(6)函数与函数的图象关于点中心对称.
(7)函数平移遵循自变量“左加右减”,函数值“上加下减”.
知识梳理·基础回归
【典例1-1】(2024·安徽淮北·二模)函数的大致图像为( )
A. B. C. D.
【答案】C
【解析】由可知,,即,
显然该函数定义域关于原点对称,
由可知,函数为奇函数,排除B, D两项,
又,排除A项,故C项正确.故选:C.
题型一:由解析式选图(识图)
【典例1-2】(2024·陕西商洛·模拟预测)函数的部分图象大致为( )
A. B. C. D.
【答案】A
【解析】当时,,故排除选项C;
当时,,故排除选项B;
令,则在上恒成立,
函数在区间上是奇函数,其函数图象关于原点对称,
故排除选项D,A选项正确.故选:A.
题型一:由解析式选图(识图)
【典例1-2】(2024·陕西商洛·模拟预测)函数的部分图象大致为( )
A. B. C. D.
【方法技巧】
利用函数的性质(如定义域、值域、奇偶性、单调性、周期性、特殊点等)排除错误选项,从而筛选出正确答案.
题型一:由解析式选图(识图)
【变式1-1】(2024·天津·二模)研究函数图象的特征,函数的图象大致为( )
A. B. C. D.
【答案】B
【解析】定义域为,即定义域关于原点对称,
且,
所以是奇函数,其图象关于原点对称,故排除CD,
注意到当时,有,即,
此时函数图象位于轴下方,故排除A,经检验B选项符合题意.故选:B.
题型一:由解析式选图(识图)
【典例2-1】(2024·安徽马鞍山·三模)已知函数的大致图象如图所示,
则的解析式可能为( )
A. B. C. D.
【答案】D
【解析】对于选项A:因为,与图象不符,故A错误;
对于选项B:因为,与图象不符,故B错误;
对于选项C:因为,与图象不符,故C错误;故选:D.
题型二:由图象选表达式
【典例2-2】(2024·宁夏固原·一模)已知函数的部分图像如图所示,则的解析式可能为( )
A. B. C. D.
【答案】A
【解析】对于B,当时,,易知,,
则,不满足图象,故B错误;
对于C,,定义域为,
又,则的图象关于轴对称,故C错误;
对于D,当时,,
由反比例函数的性质可知,在上单调递减,故D错误;
检验选项A,满足图中性质,故A正确.故选:A.
题型二:由图象选表达式
【典例2-2】(2024·宁夏固原·一模)已知函数的部分图像如图所示,则的解析式可能为( )
A. B. C. D.
【方法技巧】
1、从定义域值域判断图像位置;
2、从奇偶性判断图像的对称性;
3、从周期性判断图像循环往复;
4、从单调性判断大致变化趋势;
5、从特殊点排除错误选项.
题型二:由图象选表达式
【变式2-1】(2024·天津·二模)函数的图象如图所示,则的解析式可能为( )
A. B. C. D.
【答案】C
【解析】由图象知,该函数图象关于原点对称,所以函数为奇函数,
且,对于A,,为偶函数,故A错误;
对于B,,故B错误;
对于C,,为奇函数,当时,,
因为,在为单调递增函数,所以在单调递增,故C正确;
对于D,当时,,,所以时,,
单调递增,当时,,单调递减,故D错误,故选:C.
题型二:由图象选表达式
【典例3-1】(2024·重庆·模拟预测)已知函数,为实数,的导函数为,在同一直角坐标系中,与的大致图象不可能是( )
A. B. C. D.
【答案】C
【解析】由可得
对于,当时,在第一象限上递减,对应图象在第四象限且递增,故A项符合;对于在第一象限上与的图象在上都单调递增,故且,则.
又由可得,即与的图象交点横坐标应大于1,显然C项不符合,B, D项均符合.故选:C.
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
【答案】AB
【解析】选项A,B,C:由题意知
,
令,解得或或,
由题图可知函数的一个极值点位于区间,
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
因此,又,
所以,故,因此A,B正确,C错误.
选项D:由题图可知,
若取,则,解得,因此D错误.
故选:AB
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
【方法技巧】
根据参数的不同情况对每个选项逐一分析,推断出合理的图像位置关系,排除相互矛盾的位置关系,以得出正确选项.
题型三:表达式含参数的图象问题
【变式3-1】(多选题)(2024·安徽合肥·一模)函数的图象可能是( )
A. B. C. D.
【答案】ABD
【解析】由题意可知,函数的定义域为,
当时,,函数在上单调递增,故B正确;
当时,,,所以在上单调递增,故D正确;
当时,当时,;当时,;
故A正确;C错误.故选:ABD.
题型三:表达式含参数的图象问题
【典例4-1】如图,长方形的边,,是的中点.点沿着边,与运动,记.将动点到两点距离之和表示为的函数,
则的图像大致为( )
A. B. C. D.
【答案】B
【解析】由题意可得,,
故,由此可排除C、D;
当时点在边上,,,
所以 ,可知时图像不是线段,可排除A,故选B.
故选:B.
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
【答案】A
【解析】当点在上时,,
当点在上时,
,
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
当点在上时,,
其中A选项符合要求,B、C、D都不符合要求,故A正确.
故选:A.
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
【方法技巧】
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
题型四:函数图象应用题
【变式4-1】(2024·安徽·模拟预测)如图,直线在初始位置与等边的底边重合,之后开始在平面上按逆时针方向绕点匀速转动(转动角度不超过),它扫过的三角形内阴影部分的面积是时间的函数.这个函数的图象大致是( )
A. B. C. D.
【答案】C
【解析】如图所示,取的中点,连接,
因为为等边三角形,可得,
设等边的边长为,且,其中,
可得,
又由的面积为,可得,
且,
则的面积为,
题型四:函数图象应用题
【变式4-1】(2024·安徽·模拟预测)如图,直线在初始位置与等边的底边重合,之后开始在平面上按逆时针方向绕点匀速转动(转动角度不超过),它扫过的三角形内阴影部分的面积是时间的函数.这个函数的图象大致是( )
A. B. C. D.
令,其中,
可得,所以为单调递增函数,
又由余弦函数的性质得,当时,函数取得最小值,
所以阴影部分的面积一直在增加,但是增加速度先快后慢再快,
结合选项,可得选项C符合题意.
故选:C.
题型四:函数图象应用题
【典例5-1】(2024·北京西城·二模)将函数的图象向右平移个单位长度,所得图象再关于轴对称,得到函数的图象,则( )
A. B. C. D.
【答案】D
【解析】将函数的图象向右平移个单位长度,
所得函数为,
则函数的图象再关于轴对称得函数
.
故选:D.
题型五:函数图象的变换
【典例5-2】(2024·辽宁·三模)已知对数函数,函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,再将的图象向上平移2个单位长度,所得图象恰好与函数的图象重合,则的值是( )
A. B. C. D.
【答案】D
【解析】因为将函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,
所以,即,
将的图象向上平移2个单位长度,所得图象的函数解析式,
因为所得图象恰好与函数的图象重合,
所以,
所以,又且,解得,故选:D
题型五:函数图象的变换
【典例5-2】(2024·辽宁·三模)已知对数函数,函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,再将的图象向上平移2个单位长度,所得图象恰好与函数的图象重合,则的值是( )
A. B. C. D.
【方法技巧】
熟悉函数三种变换:(1)平移变换;(2)对称变换;(3)伸缩变换.
题型五:函数图象的变换
【变式5-1】(2024·江西赣州·二模)已知函数的图象的一部分如下左图,则如下右图的函数图象所对应的函数解析式( )
A. B. C. D.
【答案】C
【解析】
①关于y轴对称②向右平移1个单位③纵坐标不变,横坐标变为原来的一半
故选:C.
题型五:函数图象的变换
【典例6-1】(2024·全国·模拟预测)已知函数.若,,则的最小值为( )
A.1 B. C. D.2
【答案】D
【解析】画出的图象如下图所示,
令,则,
且,则,
所以且,所以,
当时,取得最小值为.故选:D.
题型六:利用函数的图像研究函数的性质、最值
【典例6-2】用表示a,b,c三个数中的最小值,则函数
的最大值是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】在一个坐标系中画出的图像,从左到右,取横坐标对应的纵坐标小的点构成新的图像,如图:
其中A点,即与的交点,其纵坐标即为所求
联立,解得,
函数的最大值为3,故选:C.
题型六:利用函数的图像研究函数的性质、最值
【典例6-2】用表示a,b,c三个数中的最小值,则函数
的最大值是( )
A.1 B.2 C.3 D.4
【方法技巧】
利用函数图像求函数的最值,先作出所涉及到的函数图像,根据题目对函数的要求,从图像上寻找取得最值的位置,计算出答案,体现了数形结合的思想.
题型六:利用函数的图像研究函数的性质、最值
【变式6-1】已知,设函数在区间上的最大值为.若,则正实数的最大值为 .
【答案】
【解析】画出的图象如下:
故,
由图象可知,当时,取得最小值,最小值为,
此时,,
则①,
故只需要②,
将①代入②得,
化简得,解得,故正实数的最大值为.
题型六:利用函数的图像研究函数的性质、最值
【典例7-1】已知函数,则满足的的取值范围为( )
A. B. C. D.
【答案】D
【解析】令,则或,
解得或或.
令,则或,
解得或.
画出函数图象的草图(如图),得满足的的取值范围为.
故选:D.
题型七:利用函数的图像解不等式
【典例7-2】(2024·重庆沙坪坝·模拟预测)已知函数,则的解集是( )
A. B. C. D.
【答案】C
【解析】根据题意当时,,
当时, ,
作出函数的图象如图,
在同一坐标系中作出函数的图象,
由图象可得不等式解集为,故选:C
题型七:利用函数的图像解不等式
【典例7-2】(2024·重庆沙坪坝·模拟预测)已知函数,则的解集是( )
A. B. C. D.
【方法技巧】
利用函数图像求解不等式的解集及参数的取值范围.先作出所涉及到的图像,求出它们的交点,根据题意结合图像写出答案.
题型七:利用函数的图像解不等式
【变式7-1】(2024·高三·江西·期中)已知函数,,则不等式的解集为( )
A. B. C. D.
【答案】A
【解析】由题知
在同一坐标系下画出,图象如下所示:
由图可知的解集为.故选:A.
题型七:利用函数的图像解不等式
【典例8-1】(2024·北京昌平·二模)已知函数若对任意的都有恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】B
【解析】因为,令,作出图象,如图所示,
令,由图知,要使对任意的都有恒成立,则必有,
当时,,由,消得到,
由,得到,即,由图可知,故选:B.
题型八:利用函数的图像求恒成立问题
【典例8-2】已知函数设若关于的不等式在上恒成立,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】由题意知,令,函数的图象如图所示,
当函数的图象经过点时,得.
当的图象与的图象相切时,
由,得,结合图形,由得.
若不等式在R上恒成立,
当时,需满足,即,
当时,需满足,即,
所以,所以实数a的取值范围为.故选:B.
题型八:利用函数的图像求恒成立问题
【典例8-2】已知函数设若关于的不等式在上恒成立,则的取值范围是( )
A. B. C. D.
【方法技巧】
先作出函数的图像,观察参数的变化怎样影响函数的形态和位置关系,找到参数的临界值,进一步得出参数的范围.
题型八:利用函数的图像求恒成立问题
【变式8-1】已知函数的定义域为,满足,且时,.若,都有,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】当时,,
因为,且时,,
所以;
当时,,
所以;
因为,
当时,,
题型八:利用函数的图像求恒成立问题
【变式8-1】已知函数的定义域为,满足,且时,.若,都有,则的取值范围是( )
A. B. C. D.
所以;
所以,得,
由此做出函数图像得:
当时,,解得或,
结合图像得的解为:或,
因为,都有,
所以.故选:B.
题型八:利用函数的图像求恒成立问题
【典例9-1】(2024·高三·重庆渝中·期中)已知函数,若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】由题意得有两个不相等的实数根,
令,当时,,,
当时,,单调递减,
当时,,单调递增,
题型九:利用函数的图像判断零点的个数
【典例9-1】(2024·高三·重庆渝中·期中)已知函数,若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. D.
且,当时,恒成立,
当时,,则,
当时,,单调递增,
且,
画出的图象如图:
要想有两个不相等的实数根,则,
故有两个不相等的实数根,则.故选:A
题型九:利用函数的图像判断零点的个数
【典例9-2】设函数,若函数恰有3个零点,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】由题意,设函数,令,即,
所以问题转化为,有3个交点;
在坐标系内,作出函数的图像如下所示,
结合图象可知,,故实数的取值范围为.
故选:B
【方法技巧】
利用函数图像判断方程解的个数.由题设条件作出所研究对象的图像,利用图像的直观性得到方程解的个数.
题型九:利用函数的图像判断零点的个数
【变式9-1】设函数,若有三个不同的实数根,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】当时,函数单调递增,函数值集合为,
当时,函数单调递减,函数值集合为,
当时,函数单调递增,函数值集合为,
作出函数的图象与直线,如图,
观察图象知,当时,函数的图象与直线有3个交点,
所以有三个不同的实数根,实数的取值范围是.
故选:C
题型九:利用函数的图像判断零点的个数
04
真题练习·命题洞见
05
课本典例·高考素材
1.已知函数.
(1)求函数的解析式;
(2)利用信息技术,画出函数的图象;
(3)求函数的零点(精确度为0.1)
【解析】(1)由题意得:
(2)函数图象如下图所示:
(3)由图象可知,函数分别在区间和区间内各有一个零点
取区间的中点,用计算器可算得
再取的中点,用计算器可算得
同理可得:,
因为
原方程在区间内的近似解可取为
同理可求得函数在区间内的零点可取为
函数满足精确度的零点为或
2.如图,是边长为2的正三角形,记位于直线左侧的图形的面积为.试求函数的解析式,并画出函数的图象.
【解析】(1)当时,
如图,设直线与分别交于、两点,则,
又,,
(2)当时,
如图,设直线与分别交于、两点,则,
又,
(3)当时,
综上所述
3.经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量),下列供求曲线,哪条表示厂商希望的供应曲线,哪条表示客户希望的需求曲线?为什么?
【解析】题图(1)中的曲线表示厂商希望的供应曲线;
题图(2)中的曲线表示客户希望的需求曲线.
从题图(1)观察,随着产品数量的上升,单价越来越高,可见是厂商希望的供应曲线;
而题图(2)恰恰相反,当产品数量逐渐上升时,单价越来越低,由此判断是客户希望的需求曲线.
4.图(1)是某条公共汽车线路收支差额y关于乘客量x的图象.
(1)试说明图(1)上点A,点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图(2)(3)所示,你能根据图象,说明这两种建议是什么吗?
【解析】(1)点A的实际意义为:当乘客量为0时,公司亏损1(单位);点B的实际意义为:当乘客量为1.5时,公司收支持平;
射线AB上的点的实际意义为:当乘客量小于1.5时,公司将亏损;当乘客量大于1.5时,公司将赢利.
(2)题图(2)的建议是:降低成本而保持票价不变;题图(3)的建议是:提高票价而保持成本不变.
易错分析·答题模板
06
易错点:图像的变换问题
易错分析:平移变换是高中数学图像变换中的基础,包括左右平移和上下平移.在平移过程中,学生常常会出现平移方向或平移单位长度的误判.学生在对称变换方面的易错点主要是对称关系的混淆.伸缩变换主要涉及图像的横向和纵向拉伸或压缩,学生在这方面的易错点主要是伸缩比例的理解和应用.翻折变换主要涉及图像沿x轴或y轴的翻折,在这方面的易错点主要是翻折轴的选择和翻折后的图像判断.
答题模板:图像的变换问题
1、模板解决思路
仔细阅读题目,然后确定题目要求的是哪种图像变换,如平移、伸缩、对称、翻折等.
2、模板解决步骤
第一步:确定变换类型,理解变换规则
第二步:分析函数表达式,绘制草图
第三步:应用变换规则,验证结果
【易错题1】已知函数,则的图象是( )
A. B. C. D.
【易错题2】要得到函数的图象,只需将函数的图象( )
A.向右平移1个单位长度,再向上平移1个单位长度
B.向右平移1个单位长度,再向下平移1个单位长度
C.向左平移1个单位长度,再向上平移1个单位长度
D.向左平移1个单位长度,再向下平移1个单位长度
C
A
感谢观看
THANK YOU
基础知识及典例
新高考数学一轮复习
函数的图象
01
考情透视·目标导航
考点要求 考题统计 考情分析
(1)函数图像的识别 (2)函数图像的应用 (3)函数图像的变换 2024年全国甲卷第7题,5分 2024年I卷第7题,5分 2023年天津卷第4题,5分 2022年天津卷第3题,5分 2022年全国乙卷第8题,5分 2022年全国甲卷第5题,5分 基本初等函数的图像是高考中的重要考点之一,是研究函数性质的重要工具.高考中总以一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等的图像为基础来考查函数图像,往往结合函数性质一并考查,考查的内容主要有知式选图、知图选式、图像变换以及灵活地应用图像判断方程解的个数,属于每年必考内容之一.
复习目标: (1)在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数. (2)会画简单的函数图象. (3)会运用函数图象研究函数的性质,解决方程解的个数与不等式解的问题.
02
知识导图·思维引航
02
03
考点突破·题型探究
(1)一次函数;
(2)二次函数;
(3)反比例函数;
(4)指数函数;
(5)对数函数;
(6)三角函数.
知识梳理·基础回归
知识点1:掌握基本初等函数的图像
1、直接画
①确定定义域;②化简解析式;③考察性质:奇偶性(或其他对称性)、单调性、周期性、凹凸性;④特殊点、极值点、与横/纵坐标交点;⑤特殊线(对称轴、渐近线等).
知识梳理·基础回归
知识点2:函数图像作法
2、图像的变换
(1)平移变换
①函数的图像是把函数的图像沿轴向左平移个单位得到的;
②函数的图像是把函数的图像沿轴向右平移个单位得到的;
③函数的图像是把函数的图像沿轴向上平移个单位得到的;
④函数的图像是把函数的图像沿轴向下平移个单位得到的;
知识梳理·基础回归
(2)对称变换
-f(x)
f(-x)
-f(-x)
logax(a>0,且a≠1)
知识梳理·基础回归
(3)翻折变换
|f(x)|
f(|x|)
知识梳理·基础回归
(4)伸缩变换
①的图像,可将的图像上的每一点的纵坐标伸长或缩短到原来的倍得到.
②的图像,可将的图像上的每一点的横坐标伸长或缩短到原来的倍得到.
知识梳理·基础回归
解题方法总结
(1)若恒成立,则的图像关于直线对称.
(2)设函数定义在实数集上,则函数与的图象关于直线对称.
(3)若,对任意恒成立,则的图象关于直线对称.
(4)函数与函数的图象关于直线对称.
(5)函数与函数的图象关于直线对称.
(6)函数与函数的图象关于点中心对称.
(7)函数平移遵循自变量“左加右减”,函数值“上加下减”.
知识梳理·基础回归
【典例1-1】(2024·安徽淮北·二模)函数的大致图像为( )
A. B. C. D.
【答案】C
【解析】由可知,,即,
显然该函数定义域关于原点对称,
由可知,函数为奇函数,排除B, D两项,
又,排除A项,故C项正确.故选:C.
题型一:由解析式选图(识图)
【典例1-2】(2024·陕西商洛·模拟预测)函数的部分图象大致为( )
A. B. C. D.
【答案】A
【解析】当时,,故排除选项C;
当时,,故排除选项B;
令,则在上恒成立,
函数在区间上是奇函数,其函数图象关于原点对称,
故排除选项D,A选项正确.故选:A.
题型一:由解析式选图(识图)
【典例1-2】(2024·陕西商洛·模拟预测)函数的部分图象大致为( )
A. B. C. D.
【方法技巧】
利用函数的性质(如定义域、值域、奇偶性、单调性、周期性、特殊点等)排除错误选项,从而筛选出正确答案.
题型一:由解析式选图(识图)
【变式1-1】(2024·天津·二模)研究函数图象的特征,函数的图象大致为( )
A. B. C. D.
【答案】B
【解析】定义域为,即定义域关于原点对称,
且,
所以是奇函数,其图象关于原点对称,故排除CD,
注意到当时,有,即,
此时函数图象位于轴下方,故排除A,经检验B选项符合题意.故选:B.
题型一:由解析式选图(识图)
【典例2-1】(2024·安徽马鞍山·三模)已知函数的大致图象如图所示,
则的解析式可能为( )
A. B. C. D.
【答案】D
【解析】对于选项A:因为,与图象不符,故A错误;
对于选项B:因为,与图象不符,故B错误;
对于选项C:因为,与图象不符,故C错误;故选:D.
题型二:由图象选表达式
【典例2-2】(2024·宁夏固原·一模)已知函数的部分图像如图所示,则的解析式可能为( )
A. B. C. D.
【答案】A
【解析】对于B,当时,,易知,,
则,不满足图象,故B错误;
对于C,,定义域为,
又,则的图象关于轴对称,故C错误;
对于D,当时,,
由反比例函数的性质可知,在上单调递减,故D错误;
检验选项A,满足图中性质,故A正确.故选:A.
题型二:由图象选表达式
【典例2-2】(2024·宁夏固原·一模)已知函数的部分图像如图所示,则的解析式可能为( )
A. B. C. D.
【方法技巧】
1、从定义域值域判断图像位置;
2、从奇偶性判断图像的对称性;
3、从周期性判断图像循环往复;
4、从单调性判断大致变化趋势;
5、从特殊点排除错误选项.
题型二:由图象选表达式
【变式2-1】(2024·天津·二模)函数的图象如图所示,则的解析式可能为( )
A. B. C. D.
【答案】C
【解析】由图象知,该函数图象关于原点对称,所以函数为奇函数,
且,对于A,,为偶函数,故A错误;
对于B,,故B错误;
对于C,,为奇函数,当时,,
因为,在为单调递增函数,所以在单调递增,故C正确;
对于D,当时,,,所以时,,
单调递增,当时,,单调递减,故D错误,故选:C.
题型二:由图象选表达式
【典例3-1】(2024·重庆·模拟预测)已知函数,为实数,的导函数为,在同一直角坐标系中,与的大致图象不可能是( )
A. B. C. D.
【答案】C
【解析】由可得
对于,当时,在第一象限上递减,对应图象在第四象限且递增,故A项符合;对于在第一象限上与的图象在上都单调递增,故且,则.
又由可得,即与的图象交点横坐标应大于1,显然C项不符合,B, D项均符合.故选:C.
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
【答案】AB
【解析】选项A,B,C:由题意知
,
令,解得或或,
由题图可知函数的一个极值点位于区间,
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
因此,又,
所以,故,因此A,B正确,C错误.
选项D:由题图可知,
若取,则,解得,因此D错误.
故选:AB
题型三:表达式含参数的图象问题
【典例3-2】(多选题)(2024·全国·模拟预测)已知函数(其中)的部分图象如图所示,则( )
A. B. C. D.
【方法技巧】
根据参数的不同情况对每个选项逐一分析,推断出合理的图像位置关系,排除相互矛盾的位置关系,以得出正确选项.
题型三:表达式含参数的图象问题
【变式3-1】(多选题)(2024·安徽合肥·一模)函数的图象可能是( )
A. B. C. D.
【答案】ABD
【解析】由题意可知,函数的定义域为,
当时,,函数在上单调递增,故B正确;
当时,,,所以在上单调递增,故D正确;
当时,当时,;当时,;
故A正确;C错误.故选:ABD.
题型三:表达式含参数的图象问题
【典例4-1】如图,长方形的边,,是的中点.点沿着边,与运动,记.将动点到两点距离之和表示为的函数,
则的图像大致为( )
A. B. C. D.
【答案】B
【解析】由题意可得,,
故,由此可排除C、D;
当时点在边上,,,
所以 ,可知时图像不是线段,可排除A,故选B.
故选:B.
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
【答案】A
【解析】当点在上时,,
当点在上时,
,
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
当点在上时,,
其中A选项符合要求,B、C、D都不符合要求,故A正确.
故选:A.
题型四:函数图象应用题
【典例4-2】 (2024·广东佛山·模拟预测)如图,点在边长为1的正方形边上运动,是的中点,当点沿运动时,点经过的路程与的面积的函数的图象的形状大致是( )
A. B. C. D.
【方法技巧】
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
题型四:函数图象应用题
【变式4-1】(2024·安徽·模拟预测)如图,直线在初始位置与等边的底边重合,之后开始在平面上按逆时针方向绕点匀速转动(转动角度不超过),它扫过的三角形内阴影部分的面积是时间的函数.这个函数的图象大致是( )
A. B. C. D.
【答案】C
【解析】如图所示,取的中点,连接,
因为为等边三角形,可得,
设等边的边长为,且,其中,
可得,
又由的面积为,可得,
且,
则的面积为,
题型四:函数图象应用题
【变式4-1】(2024·安徽·模拟预测)如图,直线在初始位置与等边的底边重合,之后开始在平面上按逆时针方向绕点匀速转动(转动角度不超过),它扫过的三角形内阴影部分的面积是时间的函数.这个函数的图象大致是( )
A. B. C. D.
令,其中,
可得,所以为单调递增函数,
又由余弦函数的性质得,当时,函数取得最小值,
所以阴影部分的面积一直在增加,但是增加速度先快后慢再快,
结合选项,可得选项C符合题意.
故选:C.
题型四:函数图象应用题
【典例5-1】(2024·北京西城·二模)将函数的图象向右平移个单位长度,所得图象再关于轴对称,得到函数的图象,则( )
A. B. C. D.
【答案】D
【解析】将函数的图象向右平移个单位长度,
所得函数为,
则函数的图象再关于轴对称得函数
.
故选:D.
题型五:函数图象的变换
【典例5-2】(2024·辽宁·三模)已知对数函数,函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,再将的图象向上平移2个单位长度,所得图象恰好与函数的图象重合,则的值是( )
A. B. C. D.
【答案】D
【解析】因为将函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,
所以,即,
将的图象向上平移2个单位长度,所得图象的函数解析式,
因为所得图象恰好与函数的图象重合,
所以,
所以,又且,解得,故选:D
题型五:函数图象的变换
【典例5-2】(2024·辽宁·三模)已知对数函数,函数的图象上所有点的纵坐标不变,横坐标扩大为原来的3倍,得到函数的图象,再将的图象向上平移2个单位长度,所得图象恰好与函数的图象重合,则的值是( )
A. B. C. D.
【方法技巧】
熟悉函数三种变换:(1)平移变换;(2)对称变换;(3)伸缩变换.
题型五:函数图象的变换
【变式5-1】(2024·江西赣州·二模)已知函数的图象的一部分如下左图,则如下右图的函数图象所对应的函数解析式( )
A. B. C. D.
【答案】C
【解析】
①关于y轴对称②向右平移1个单位③纵坐标不变,横坐标变为原来的一半
故选:C.
题型五:函数图象的变换
【典例6-1】(2024·全国·模拟预测)已知函数.若,,则的最小值为( )
A.1 B. C. D.2
【答案】D
【解析】画出的图象如下图所示,
令,则,
且,则,
所以且,所以,
当时,取得最小值为.故选:D.
题型六:利用函数的图像研究函数的性质、最值
【典例6-2】用表示a,b,c三个数中的最小值,则函数
的最大值是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】在一个坐标系中画出的图像,从左到右,取横坐标对应的纵坐标小的点构成新的图像,如图:
其中A点,即与的交点,其纵坐标即为所求
联立,解得,
函数的最大值为3,故选:C.
题型六:利用函数的图像研究函数的性质、最值
【典例6-2】用表示a,b,c三个数中的最小值,则函数
的最大值是( )
A.1 B.2 C.3 D.4
【方法技巧】
利用函数图像求函数的最值,先作出所涉及到的函数图像,根据题目对函数的要求,从图像上寻找取得最值的位置,计算出答案,体现了数形结合的思想.
题型六:利用函数的图像研究函数的性质、最值
【变式6-1】已知,设函数在区间上的最大值为.若,则正实数的最大值为 .
【答案】
【解析】画出的图象如下:
故,
由图象可知,当时,取得最小值,最小值为,
此时,,
则①,
故只需要②,
将①代入②得,
化简得,解得,故正实数的最大值为.
题型六:利用函数的图像研究函数的性质、最值
【典例7-1】已知函数,则满足的的取值范围为( )
A. B. C. D.
【答案】D
【解析】令,则或,
解得或或.
令,则或,
解得或.
画出函数图象的草图(如图),得满足的的取值范围为.
故选:D.
题型七:利用函数的图像解不等式
【典例7-2】(2024·重庆沙坪坝·模拟预测)已知函数,则的解集是( )
A. B. C. D.
【答案】C
【解析】根据题意当时,,
当时, ,
作出函数的图象如图,
在同一坐标系中作出函数的图象,
由图象可得不等式解集为,故选:C
题型七:利用函数的图像解不等式
【典例7-2】(2024·重庆沙坪坝·模拟预测)已知函数,则的解集是( )
A. B. C. D.
【方法技巧】
利用函数图像求解不等式的解集及参数的取值范围.先作出所涉及到的图像,求出它们的交点,根据题意结合图像写出答案.
题型七:利用函数的图像解不等式
【变式7-1】(2024·高三·江西·期中)已知函数,,则不等式的解集为( )
A. B. C. D.
【答案】A
【解析】由题知
在同一坐标系下画出,图象如下所示:
由图可知的解集为.故选:A.
题型七:利用函数的图像解不等式
【典例8-1】(2024·北京昌平·二模)已知函数若对任意的都有恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】B
【解析】因为,令,作出图象,如图所示,
令,由图知,要使对任意的都有恒成立,则必有,
当时,,由,消得到,
由,得到,即,由图可知,故选:B.
题型八:利用函数的图像求恒成立问题
【典例8-2】已知函数设若关于的不等式在上恒成立,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】由题意知,令,函数的图象如图所示,
当函数的图象经过点时,得.
当的图象与的图象相切时,
由,得,结合图形,由得.
若不等式在R上恒成立,
当时,需满足,即,
当时,需满足,即,
所以,所以实数a的取值范围为.故选:B.
题型八:利用函数的图像求恒成立问题
【典例8-2】已知函数设若关于的不等式在上恒成立,则的取值范围是( )
A. B. C. D.
【方法技巧】
先作出函数的图像,观察参数的变化怎样影响函数的形态和位置关系,找到参数的临界值,进一步得出参数的范围.
题型八:利用函数的图像求恒成立问题
【变式8-1】已知函数的定义域为,满足,且时,.若,都有,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】当时,,
因为,且时,,
所以;
当时,,
所以;
因为,
当时,,
题型八:利用函数的图像求恒成立问题
【变式8-1】已知函数的定义域为,满足,且时,.若,都有,则的取值范围是( )
A. B. C. D.
所以;
所以,得,
由此做出函数图像得:
当时,,解得或,
结合图像得的解为:或,
因为,都有,
所以.故选:B.
题型八:利用函数的图像求恒成立问题
【典例9-1】(2024·高三·重庆渝中·期中)已知函数,若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】由题意得有两个不相等的实数根,
令,当时,,,
当时,,单调递减,
当时,,单调递增,
题型九:利用函数的图像判断零点的个数
【典例9-1】(2024·高三·重庆渝中·期中)已知函数,若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. D.
且,当时,恒成立,
当时,,则,
当时,,单调递增,
且,
画出的图象如图:
要想有两个不相等的实数根,则,
故有两个不相等的实数根,则.故选:A
题型九:利用函数的图像判断零点的个数
【典例9-2】设函数,若函数恰有3个零点,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】由题意,设函数,令,即,
所以问题转化为,有3个交点;
在坐标系内,作出函数的图像如下所示,
结合图象可知,,故实数的取值范围为.
故选:B
【方法技巧】
利用函数图像判断方程解的个数.由题设条件作出所研究对象的图像,利用图像的直观性得到方程解的个数.
题型九:利用函数的图像判断零点的个数
【变式9-1】设函数,若有三个不同的实数根,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】当时,函数单调递增,函数值集合为,
当时,函数单调递减,函数值集合为,
当时,函数单调递增,函数值集合为,
作出函数的图象与直线,如图,
观察图象知,当时,函数的图象与直线有3个交点,
所以有三个不同的实数根,实数的取值范围是.
故选:C
题型九:利用函数的图像判断零点的个数
04
真题练习·命题洞见
05
课本典例·高考素材
1.已知函数.
(1)求函数的解析式;
(2)利用信息技术,画出函数的图象;
(3)求函数的零点(精确度为0.1)
【解析】(1)由题意得:
(2)函数图象如下图所示:
(3)由图象可知,函数分别在区间和区间内各有一个零点
取区间的中点,用计算器可算得
再取的中点,用计算器可算得
同理可得:,
因为
原方程在区间内的近似解可取为
同理可求得函数在区间内的零点可取为
函数满足精确度的零点为或
2.如图,是边长为2的正三角形,记位于直线左侧的图形的面积为.试求函数的解析式,并画出函数的图象.
【解析】(1)当时,
如图,设直线与分别交于、两点,则,
又,,
(2)当时,
如图,设直线与分别交于、两点,则,
又,
(3)当时,
综上所述
3.经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量),下列供求曲线,哪条表示厂商希望的供应曲线,哪条表示客户希望的需求曲线?为什么?
【解析】题图(1)中的曲线表示厂商希望的供应曲线;
题图(2)中的曲线表示客户希望的需求曲线.
从题图(1)观察,随着产品数量的上升,单价越来越高,可见是厂商希望的供应曲线;
而题图(2)恰恰相反,当产品数量逐渐上升时,单价越来越低,由此判断是客户希望的需求曲线.
4.图(1)是某条公共汽车线路收支差额y关于乘客量x的图象.
(1)试说明图(1)上点A,点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图(2)(3)所示,你能根据图象,说明这两种建议是什么吗?
【解析】(1)点A的实际意义为:当乘客量为0时,公司亏损1(单位);点B的实际意义为:当乘客量为1.5时,公司收支持平;
射线AB上的点的实际意义为:当乘客量小于1.5时,公司将亏损;当乘客量大于1.5时,公司将赢利.
(2)题图(2)的建议是:降低成本而保持票价不变;题图(3)的建议是:提高票价而保持成本不变.
易错分析·答题模板
06
易错点:图像的变换问题
易错分析:平移变换是高中数学图像变换中的基础,包括左右平移和上下平移.在平移过程中,学生常常会出现平移方向或平移单位长度的误判.学生在对称变换方面的易错点主要是对称关系的混淆.伸缩变换主要涉及图像的横向和纵向拉伸或压缩,学生在这方面的易错点主要是伸缩比例的理解和应用.翻折变换主要涉及图像沿x轴或y轴的翻折,在这方面的易错点主要是翻折轴的选择和翻折后的图像判断.
答题模板:图像的变换问题
1、模板解决思路
仔细阅读题目,然后确定题目要求的是哪种图像变换,如平移、伸缩、对称、翻折等.
2、模板解决步骤
第一步:确定变换类型,理解变换规则
第二步:分析函数表达式,绘制草图
第三步:应用变换规则,验证结果
【易错题1】已知函数,则的图象是( )
A. B. C. D.
【易错题2】要得到函数的图象,只需将函数的图象( )
A.向右平移1个单位长度,再向上平移1个单位长度
B.向右平移1个单位长度,再向下平移1个单位长度
C.向左平移1个单位长度,再向上平移1个单位长度
D.向左平移1个单位长度,再向下平移1个单位长度
C
A
感谢观看
THANK YOU
同课章节目录
