新高考高三数学对数与对数函数一轮复习课件(共67张PPT)
文档属性
| 名称 | 新高考高三数学对数与对数函数一轮复习课件(共67张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 11:04:26 | ||
图片预览







文档简介
(共67张PPT)
基础知识及典例
新高考数学一轮复习
对数与对数函数
01
考情透视·目标导航
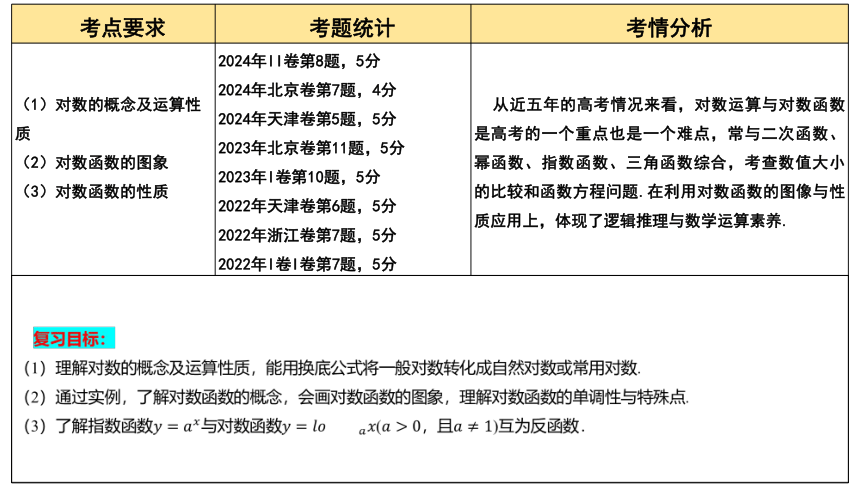
考点要求 考题统计 考情分析
(1)对数的概念及运算性质 (2)对数函数的图象 (3)对数函数的性质 2024年II卷第8题,5分 2024年北京卷第7题,4分 2024年天津卷第5题,5分 2023年北京卷第11题,5分 2023年I卷第10题,5分 2022年天津卷第6题,5分 2022年浙江卷第7题,5分 2022年I卷I卷第7题,5分 从近五年的高考情况来看,对数运算与对数函数是高考的一个重点也是一个难点,常与二次函数、幂函数、指数函数、三角函数综合,考查数值大小的比较和函数方程问题.在利用对数函数的图像与性质应用上,体现了逻辑推理与数学运算素养.
复习目标: (1)理解对数的概念及运算性质,能用换底公式将一般对数转化成自然对数或常用对数. (2)通过实例,了解对数函数的概念,会画对数函数的图象,理解对数函数的单调性与特殊点. (3)了解指数函数与对数函数(,且)互为反函数.
02
知识导图·思维引航
02
03
考点突破·题型探究
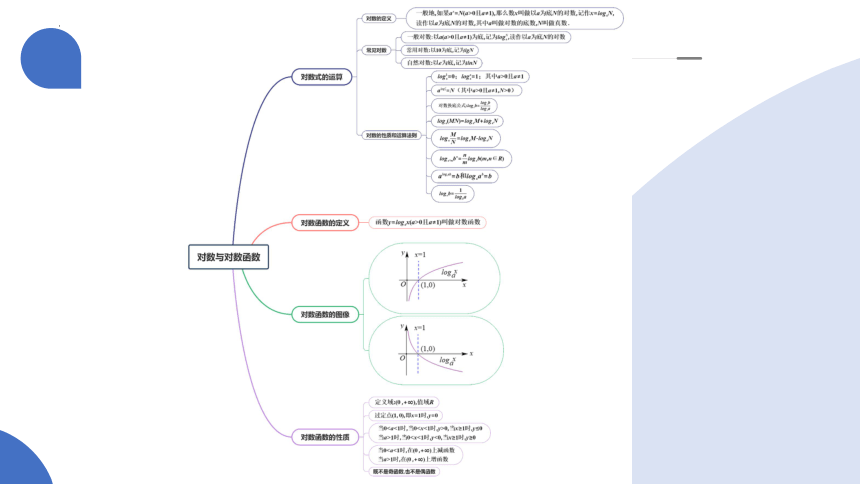
1.对数的定义
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作
,其中 叫做对数的底数, 叫做真数.
以10为底的对数叫做常用对数,记作 .
以e为底的对数叫做自然对数,记作 .
x=logaN
a
N
lg N
ln N
知识梳理·基础回归
知识点1:对数式的运算
2.对数的性质与运算性质
①;;其中且;
②(其中且,);
③对数换底公式:;
④;
⑤;
⑥,;
⑦和;
⑧;
知识梳理·基础回归
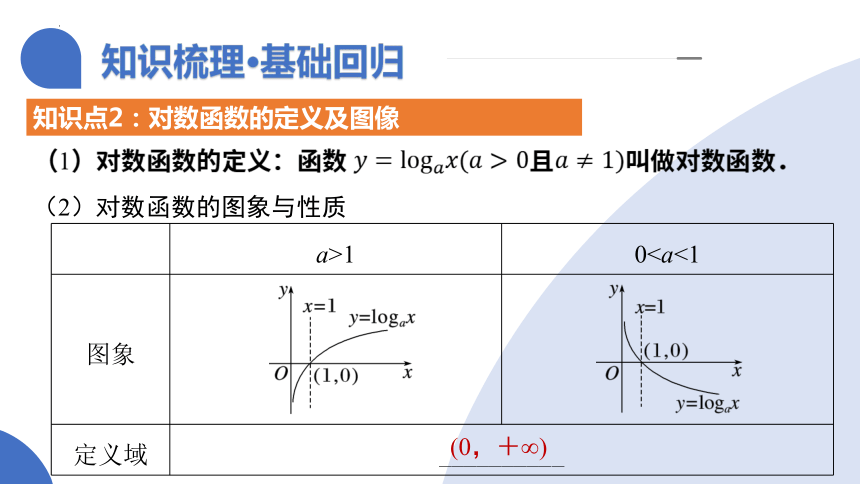
(1)对数函数的定义:函数 且叫做对数函数.
(2)对数函数的图象与性质
a>1 0图象
定义域 __________
(0,+∞)
知识梳理·基础回归
知识点2:对数函数的定义及图像
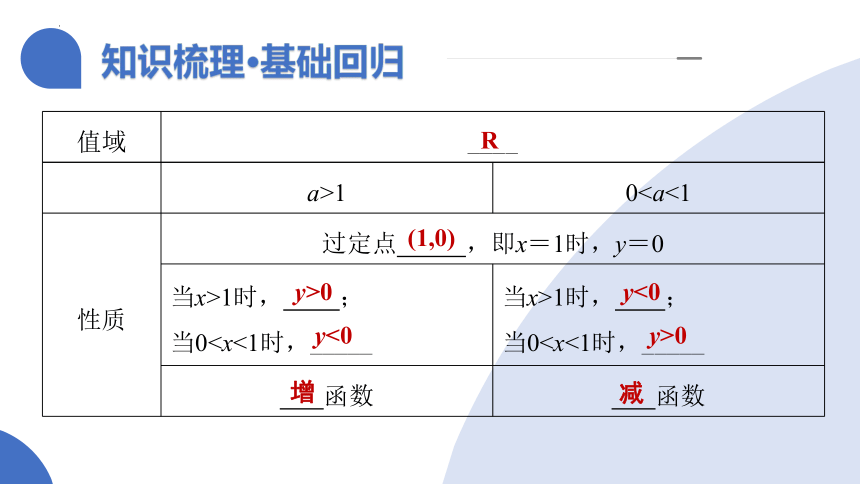
a>1 0性质 过定点 ,即x=1时,y=0
当x>1时, ; 当01时, ;
当0函数 函数
(1,0)
y>0
y<0
y<0
y>0
增
减
值域 ____
R
知识梳理·基础回归
(3)反函数
指数函数y=ax(a>0,且a≠1)与对数函数y= (a>0,且a≠1)互为反函数,它们的图象关于直线 对称.
logax
y=x
知识梳理·基础回归
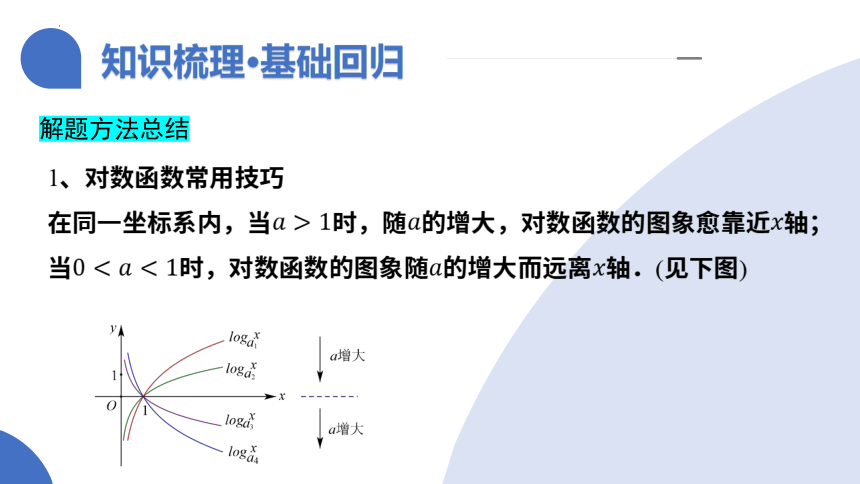
1、对数函数常用技巧
在同一坐标系内,当时,随的增大,对数函数的图象愈靠近轴;
当时,对数函数的图象随的增大而远离轴.(见下图)
解题方法总结
知识梳理·基础回归
【典例1-1】已知,则 .(用含的式子表示)
【答案】
【解析】因为,所以,又,
所以
.
故答案为:
题型一:对数式的运算
【典例1-2】(2024·重庆·三模)若正实数,满足,,则 .
【答案】100
【解析】由于,整理得,①,
又,②,
所以①+②得:;即
对于取常用对数可得,,
故.
【方法技巧】 对数的有关运算问题要注意公式的正用、逆用及变形等应用.
题型一:对数式的运算
【变式1-1】化简下列各式:
(1);
(2).
【解析】(1)原式.
(2)原式
.
题型一:对数式的运算
【变式1-2】已知,,则 .(用表示)
【答案】
【解析】因为,所以,
又,所以
.
故答案为:
题型一:对数式的运算
【典例2-1】已知函数① y=logax;② y=logbx;③ y=logcx;④ y=logdx的大致图象如图所示,则下列不等关系正确的是( )
A.a+c<b+a B.a+d<b+c
C.b+c<a+d D.b+d<a+c
【答案】A
【解析】由已知可得b>a>1>d>c,则a+b>a+c,b+d>a+c,故A正确,D错误;又a+d与b+c的大小不确定,故B,C错误.故选A.
题型二:对数函数的图象及应用
【典例2-2】(2024·江苏扬州·模拟预测)设方程和方程的根分别为,设函数,则( )
A. B.
C. D.
【答案】B
【解析】由得,由得,
所以令,这3个函数图象情况如下图所示:
设交于点,交于点,
由于的图象关于直线对称,
而的交点为,所以,
题型二:对数函数的图象及应用
【典例2-2】(2024·江苏扬州·模拟预测)设方程和方程的根分别为,设函数,则( )
A. B.
C. D.
注意到函数的对称轴为直线,
即,且二次函数的图象是开口向上的抛物线方程,
从而.故选:B.
【方法技巧】
对于有关对数型函数的图象问题,一般是从最基本的对数函数的图象入手,通过伸缩、平移、对称等变换得到,当时,对数函数的图像呈上升趋势;当时,对数函数的图像呈下降趋势.
题型二:对数函数的图象及应用
【变式2-1】(多选题)(2024·河南信阳·模拟预测)函数的大致图象不可能为( )
A. B. C. D.
【答案】BCD
【解析】函数的定义域为,
因为,所以函数为偶函数,
当时,为减函数,且过定点,
故函数的大致图象不可能为BCD选项.
故选:BCD.
题型二:对数函数的图象及应用
【变式2-2】(2024·高三·江西南昌·开学考试)已知函数和的图象与直线交点的横坐标分别为,,则( )
A. B. C. D.
【答案】D
【解析】作出函数和的图象以及直线的图象,如图,
由函数和的图象与直线交点的横坐标分别为,,
结合图象可知,A错误;
由题意知,也即,
由于函数和互为反函数,
二者图象关于直线对称,而为和的图象与直线的交点,
题型二:对数函数的图象及应用
【变式2-2】(2024·高三·江西南昌·开学考试)已知函数和的图象与直线交点的横坐标分别为,,则( )
A. B. C. D.
故关于对称,故,B错误;
由,故,C错误;
因为,故,
结合,即得,D正确,
故选:D
题型二:对数函数的图象及应用
【典例3-1】函数 (且)的图象必经过一个定点,则这个定点的坐标是( )
A. B. C. D.
【答案】C
【解析】因为对数函数(且)恒过定点,
所以函数 (且)的图象必过定点.
故选:C.
题型三:对数函数过定点问题
【典例3-2】函数(且)的图象恒过定点,若且,,则的最小值为( )
A.9 B.8 C. D.
【答案】B
【解析】当时,,
函数过定点,得,所以,
因为,,
所以,,
当且仅当,即时,等号成立,
所以,的最小值为8.故选:B
题型三:对数函数过定点问题
【方法技巧】
恒过定点.
【变式3-1】函数的图象恒过定点,若点在直线上,其中,则的最小值为( )
A. B.3 C.7 D.4
【答案】A
【解析】对于函数,
当时,,所以,则,
所以,
当且仅当时等号成立.故选:A
题型三:对数函数过定点问题
【变式3-2】已知直线经过函数图象过的定点(其中均大于0),则的最小值为( )
A.2 B.3 C.4 D.5
【答案】C
【解析】因为,
所以函数图象过的定点为,
将其代入直线方程得,即,
又,
所以,
当且仅当即时,等号成立,故有最小值4.
故选:C.
题型三:对数函数过定点问题
【典例4-1】(2024·黑龙江哈尔滨·模拟预测)设,,,
则( )
A. B. C. D.
【答案】C
【解析】∵,
,
则,故选:C.
题型四:比较对数式的大小
【典例4-2】已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【解析】因为,,∴,
因为,∴,
∴.故选:D.
题型四:比较对数式的大小
【方法技巧】
比较大小问题,常利用函数的单调性及中间值法.
【变式4-1】(2024·天津·二模)设,则的大小关系为( )
A. B. C. D.
【答案】C
【解析】,
,
,,.故选:C.
题型四:比较对数式的大小
【变式4-2】(2024·宁夏银川·三模)已知,,,则( )
A. B. C. D.
【答案】D
【解析】由题知,,,因为在定义域内单调递增,
所以,即,
因为在定义域内单调递减,所以,
即,
因为在上单调递减,所以,即,
综上:.故选:D
题型四:比较对数式的大小
【典例5-1】方程的解是 .
【答案】
【解析】由方程,可得,
,解得.
故答案为:
题型五:解对数方程或不等式
【典例5-2】不等式的解集为 .
【答案】
【解析】设函数,
则应有,解得,所以,定义域为.
又,
所以,由,可得.
因为以及均在上单调递增,
所以,在上单调递增,所以,.
综上所述,.所以,不等式的解集为.
题型五:解对数方程或不等式
【典例5-2】不等式的解集为 .
【方法技巧】
(1)对于形如的形式,利用转化;对于形如的形式,可借助换元法转化为二次方程求解.
(2)解对数不等式,也是利用对数函数的单调性将不等式转化为比较真数之间的不等式,再解这个不等式即可.
题型五:解对数方程或不等式
【变式5-1】不等式的解集是 .
【答案】
【解析】设,其定义域为,
和在均为增函数,
则在为增函数,且,
,即,,
不等式的解集是.
故答案为:.
题型五:解对数方程或不等式
【变式5-2】方程:的解是 .
【答案】
【解析】因为,即,
所以,
即,解得,则,或无实根.
故答案为:
题型五:解对数方程或不等式
【变式5-3】不等式的解集是 .
【答案】或
【解析】原不等式可化为,即,
∴,于是,亦即或,
∴或,故解集为或
故答案为:或
题型五:解对数方程或不等式
【典例6-1】(2024·全国·模拟预测)已知函数在区间上有最大值或最小值,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】要使函数在区间上有最大值或最小值,
由于开口向上,
故需函数在区间上有最小值,且.
该函数图像的对称轴为直线,所以,解得,
所以,且,即实数的取值范围为.故选:B.
题型六:对数函数的最值与值域问题
【典例6-2】已知函数的最大值为2,则 .
【答案】6
【解析】因为函数由
与复合而成,
而在定义域上单调递增,所以当取最大值时,
函数取得最大值,
由二次函数的性质易知当时,,此时,
所以,解得.
【方法技巧】
对数函数的最值与值域问题通常利用对数函数的单调性解决.
题型六:对数函数的最值与值域问题
【变式6-1】若函数(且)的最小值为-4,则实数a的值为 .
【答案】
【解析】由题意知,,解得,
因为,
因为,则,又因为的最小值为-4,
则,所以,
即,得,
因为,所以.
题型六:对数函数的最值与值域问题
【变式6-2】已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【解析】(1)当时,函数恒有意义,
所以在上恒成立,
即在上恒成立.
令,,则,
所以在上单调递减,所以,所以.
又且,所以.
题型六:对数函数的最值与值域问题
【变式6-2】已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【解析】(2)函数在区间上有意义,则在上恒成立.
由(1)同理可知,,
又函数在区间上为减函数,并且最大值为.
当时,为减函数,则且在上单调递增,
所以,即,故不存在这样的实数;
当时,为增函数,则且在上单调递减,
所以,即,故不存在这样的实数.
综上,不存在这样的实数,使得函数在区间上为减函数,且最大值为.
题型六:对数函数的最值与值域问题
【典例7-1】已知函数,若对任意都有,则实数a的取值范围是( )
A. B. C. D.
【答案】D
【解析】因为若对任意,都有,
所以对任意,都有,
令,
则在上单调递增.
首先.
题型七:对数函数中的恒成立问题
【典例7-1】已知函数,若对任意都有,则实数a的取值范围是( )
A. B. C. D.
因为在上递增,所以在上递增.
当时,显然符合题意;
当时,令,
则在上递增,所以,则.
综上所述,,故D正确.
故选:D.
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
【答案】C
【解析】变形为:,
即在上恒成立,
若,此时在上单调递减,
,
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
而当时,,显然不合题意;
当时,画出两个函数的图像,
要想满足在上恒成立,
只需,即,
解得:,综上:实数a的取值范围是.故选:C
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
【方法技巧】
已知不等式能恒成立求参数值(取值范围)问题常用的方法:
(1)函数法:讨论参数范围,通常借助函数单调性求解;
(2)分离参数法:首先将参数分离,转化成求函数的最值或值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,再利用数形结合的方法来解决.
题型七:对数函数中的恒成立问题
【变式7-1】已知函数,且,若对任意的,存在,使得成立,则实数的取值范围是 .
【答案】
【解析】根据题意知,
因为,其图象开口向下,对称轴为,
所以当时,其最小值,
当时,,在上的最小值为,
则由得,
当时,,在上的最小值为,则时,无解,
故实数的取值范围为.
题型七:对数函数中的恒成立问题
【变式7-2】已知且,当时,,则的取值范围为 .
【答案】
【解析】当时,.
当时,成立.
当时,若成立,是减函数,是增函数,则,解得,所以.
综上,的取值范围为.
题型七:对数函数中的恒成立问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
【答案】B
【解析】由题意知,,
,
令,则,
又因为与互为反函数,
所以、分别与的的交点关于对称,
所以,即:,
又因为,,
所以由零点存在性定理可知,,
题型八:对数函数的综合问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
又因为,即,
所以,
对于A项,因为,,
所以,故A项错误;
对于B项,因为,所以,
又因为,,
所以,故B项正确;
题型八:对数函数的综合问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
对于C项,因为,,
所以,故C项错误;
对于D项,因为, ,,
所以,故D项错误.故选:B.
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
【答案】D
【解析】当时,,
由复合函数的单调性可知在上单调递减,
所以;
当时,,
因为在上单调递增,为增函数,
所以在上单调递增,
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
又在上为增函数,所以在单调递增,
所以.
综上,在上恒成立,当且仅当时取等号.
所以不等式,
解得且且,即原不等式的解集为.
故选:D
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
【方法技巧】
对数函数常与其他函数形成复合函数问题,解题时要清楚复合的层次,外层是对数函数还是内层是对数函数,其次如果涉及到定义域、值域、奇偶性、单调性等问题,则要按复合函数的性质规律求解.
题型八:对数函数的综合问题
【变式8-1】设定义域为R的函数,若关于x的方程有8个不同的实根,到实数b的取值范围是 .
【答案】
【解析】由题设,的图象如图所示:
令,则化为
,∴要使原方程有8个不同实根,
则有2个不同的实根且两根、,
题型八:对数函数的综合问题
【变式8-1】设定义域为R的函数,若关于x的方程有8个不同的实根,到实数b的取值范围是 .
∴,可得,
又在上递减,在上递增,且,
即,综上,.
题型八:对数函数的综合问题
04
真题练习·命题洞见
05
课本典例·高考素材
1.我们可以把看作每天的"进步”率都是1%,一年后是;而把看作每天的“落后”率都是1%,一年后是.利用计算工具计算并回答下列问题:
(1)一年后“进步”的是“落后”的多少倍?
(2)大约经过多少天后“进步”的分别是“落后”的10倍、100倍、1000倍?
【解析】(1).
∴一年后“进步”的大约是“落后”的倍
(2)由得,
∴大约经过天“进步”的是“落后”的倍.
由得.
∴大约经过天“进步”的是“落后”的倍.
由得解得
∴大约经过天“进步”的是“落后”的倍.
3.已知, , ,求实数a的取值范围.
【解析】解:,
当时成立;
②当时,解得.
又,
∴a的取值范围是.
06
易错分析·答题模板
答题模板:对数型复合函数的单调问题
1、模板解决思路
判断复合函数单调性的原则是“同增异减”.
2、模板解决步骤
第一步:求函数的定义域.
第二步:将函数分解成内层函数和外层函数.
第三步:判断内层函数和外层函数的单调性.
第四步:根据“同增异减”的原则确定复合函数的单调性.
【典例1】若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
【典例2】已知函数在上单调递减,则实数a的取值范围为( )
A. B. C. D.
B
A
感谢观看
THANK YOU
基础知识及典例
新高考数学一轮复习
对数与对数函数
01
考情透视·目标导航
考点要求 考题统计 考情分析
(1)对数的概念及运算性质 (2)对数函数的图象 (3)对数函数的性质 2024年II卷第8题,5分 2024年北京卷第7题,4分 2024年天津卷第5题,5分 2023年北京卷第11题,5分 2023年I卷第10题,5分 2022年天津卷第6题,5分 2022年浙江卷第7题,5分 2022年I卷I卷第7题,5分 从近五年的高考情况来看,对数运算与对数函数是高考的一个重点也是一个难点,常与二次函数、幂函数、指数函数、三角函数综合,考查数值大小的比较和函数方程问题.在利用对数函数的图像与性质应用上,体现了逻辑推理与数学运算素养.
复习目标: (1)理解对数的概念及运算性质,能用换底公式将一般对数转化成自然对数或常用对数. (2)通过实例,了解对数函数的概念,会画对数函数的图象,理解对数函数的单调性与特殊点. (3)了解指数函数与对数函数(,且)互为反函数.
02
知识导图·思维引航
02
03
考点突破·题型探究
1.对数的定义
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作
,其中 叫做对数的底数, 叫做真数.
以10为底的对数叫做常用对数,记作 .
以e为底的对数叫做自然对数,记作 .
x=logaN
a
N
lg N
ln N
知识梳理·基础回归
知识点1:对数式的运算
2.对数的性质与运算性质
①;;其中且;
②(其中且,);
③对数换底公式:;
④;
⑤;
⑥,;
⑦和;
⑧;
知识梳理·基础回归
(1)对数函数的定义:函数 且叫做对数函数.
(2)对数函数的图象与性质
a>1 0
定义域 __________
(0,+∞)
知识梳理·基础回归
知识点2:对数函数的定义及图像
a>1 0
当x>1时, ; 当0
当0
(1,0)
y>0
y<0
y<0
y>0
增
减
值域 ____
R
知识梳理·基础回归
(3)反函数
指数函数y=ax(a>0,且a≠1)与对数函数y= (a>0,且a≠1)互为反函数,它们的图象关于直线 对称.
logax
y=x
知识梳理·基础回归
1、对数函数常用技巧
在同一坐标系内,当时,随的增大,对数函数的图象愈靠近轴;
当时,对数函数的图象随的增大而远离轴.(见下图)
解题方法总结
知识梳理·基础回归
【典例1-1】已知,则 .(用含的式子表示)
【答案】
【解析】因为,所以,又,
所以
.
故答案为:
题型一:对数式的运算
【典例1-2】(2024·重庆·三模)若正实数,满足,,则 .
【答案】100
【解析】由于,整理得,①,
又,②,
所以①+②得:;即
对于取常用对数可得,,
故.
【方法技巧】 对数的有关运算问题要注意公式的正用、逆用及变形等应用.
题型一:对数式的运算
【变式1-1】化简下列各式:
(1);
(2).
【解析】(1)原式.
(2)原式
.
题型一:对数式的运算
【变式1-2】已知,,则 .(用表示)
【答案】
【解析】因为,所以,
又,所以
.
故答案为:
题型一:对数式的运算
【典例2-1】已知函数① y=logax;② y=logbx;③ y=logcx;④ y=logdx的大致图象如图所示,则下列不等关系正确的是( )
A.a+c<b+a B.a+d<b+c
C.b+c<a+d D.b+d<a+c
【答案】A
【解析】由已知可得b>a>1>d>c,则a+b>a+c,b+d>a+c,故A正确,D错误;又a+d与b+c的大小不确定,故B,C错误.故选A.
题型二:对数函数的图象及应用
【典例2-2】(2024·江苏扬州·模拟预测)设方程和方程的根分别为,设函数,则( )
A. B.
C. D.
【答案】B
【解析】由得,由得,
所以令,这3个函数图象情况如下图所示:
设交于点,交于点,
由于的图象关于直线对称,
而的交点为,所以,
题型二:对数函数的图象及应用
【典例2-2】(2024·江苏扬州·模拟预测)设方程和方程的根分别为,设函数,则( )
A. B.
C. D.
注意到函数的对称轴为直线,
即,且二次函数的图象是开口向上的抛物线方程,
从而.故选:B.
【方法技巧】
对于有关对数型函数的图象问题,一般是从最基本的对数函数的图象入手,通过伸缩、平移、对称等变换得到,当时,对数函数的图像呈上升趋势;当时,对数函数的图像呈下降趋势.
题型二:对数函数的图象及应用
【变式2-1】(多选题)(2024·河南信阳·模拟预测)函数的大致图象不可能为( )
A. B. C. D.
【答案】BCD
【解析】函数的定义域为,
因为,所以函数为偶函数,
当时,为减函数,且过定点,
故函数的大致图象不可能为BCD选项.
故选:BCD.
题型二:对数函数的图象及应用
【变式2-2】(2024·高三·江西南昌·开学考试)已知函数和的图象与直线交点的横坐标分别为,,则( )
A. B. C. D.
【答案】D
【解析】作出函数和的图象以及直线的图象,如图,
由函数和的图象与直线交点的横坐标分别为,,
结合图象可知,A错误;
由题意知,也即,
由于函数和互为反函数,
二者图象关于直线对称,而为和的图象与直线的交点,
题型二:对数函数的图象及应用
【变式2-2】(2024·高三·江西南昌·开学考试)已知函数和的图象与直线交点的横坐标分别为,,则( )
A. B. C. D.
故关于对称,故,B错误;
由,故,C错误;
因为,故,
结合,即得,D正确,
故选:D
题型二:对数函数的图象及应用
【典例3-1】函数 (且)的图象必经过一个定点,则这个定点的坐标是( )
A. B. C. D.
【答案】C
【解析】因为对数函数(且)恒过定点,
所以函数 (且)的图象必过定点.
故选:C.
题型三:对数函数过定点问题
【典例3-2】函数(且)的图象恒过定点,若且,,则的最小值为( )
A.9 B.8 C. D.
【答案】B
【解析】当时,,
函数过定点,得,所以,
因为,,
所以,,
当且仅当,即时,等号成立,
所以,的最小值为8.故选:B
题型三:对数函数过定点问题
【方法技巧】
恒过定点.
【变式3-1】函数的图象恒过定点,若点在直线上,其中,则的最小值为( )
A. B.3 C.7 D.4
【答案】A
【解析】对于函数,
当时,,所以,则,
所以,
当且仅当时等号成立.故选:A
题型三:对数函数过定点问题
【变式3-2】已知直线经过函数图象过的定点(其中均大于0),则的最小值为( )
A.2 B.3 C.4 D.5
【答案】C
【解析】因为,
所以函数图象过的定点为,
将其代入直线方程得,即,
又,
所以,
当且仅当即时,等号成立,故有最小值4.
故选:C.
题型三:对数函数过定点问题
【典例4-1】(2024·黑龙江哈尔滨·模拟预测)设,,,
则( )
A. B. C. D.
【答案】C
【解析】∵,
,
则,故选:C.
题型四:比较对数式的大小
【典例4-2】已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【解析】因为,,∴,
因为,∴,
∴.故选:D.
题型四:比较对数式的大小
【方法技巧】
比较大小问题,常利用函数的单调性及中间值法.
【变式4-1】(2024·天津·二模)设,则的大小关系为( )
A. B. C. D.
【答案】C
【解析】,
,
,,.故选:C.
题型四:比较对数式的大小
【变式4-2】(2024·宁夏银川·三模)已知,,,则( )
A. B. C. D.
【答案】D
【解析】由题知,,,因为在定义域内单调递增,
所以,即,
因为在定义域内单调递减,所以,
即,
因为在上单调递减,所以,即,
综上:.故选:D
题型四:比较对数式的大小
【典例5-1】方程的解是 .
【答案】
【解析】由方程,可得,
,解得.
故答案为:
题型五:解对数方程或不等式
【典例5-2】不等式的解集为 .
【答案】
【解析】设函数,
则应有,解得,所以,定义域为.
又,
所以,由,可得.
因为以及均在上单调递增,
所以,在上单调递增,所以,.
综上所述,.所以,不等式的解集为.
题型五:解对数方程或不等式
【典例5-2】不等式的解集为 .
【方法技巧】
(1)对于形如的形式,利用转化;对于形如的形式,可借助换元法转化为二次方程求解.
(2)解对数不等式,也是利用对数函数的单调性将不等式转化为比较真数之间的不等式,再解这个不等式即可.
题型五:解对数方程或不等式
【变式5-1】不等式的解集是 .
【答案】
【解析】设,其定义域为,
和在均为增函数,
则在为增函数,且,
,即,,
不等式的解集是.
故答案为:.
题型五:解对数方程或不等式
【变式5-2】方程:的解是 .
【答案】
【解析】因为,即,
所以,
即,解得,则,或无实根.
故答案为:
题型五:解对数方程或不等式
【变式5-3】不等式的解集是 .
【答案】或
【解析】原不等式可化为,即,
∴,于是,亦即或,
∴或,故解集为或
故答案为:或
题型五:解对数方程或不等式
【典例6-1】(2024·全国·模拟预测)已知函数在区间上有最大值或最小值,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】要使函数在区间上有最大值或最小值,
由于开口向上,
故需函数在区间上有最小值,且.
该函数图像的对称轴为直线,所以,解得,
所以,且,即实数的取值范围为.故选:B.
题型六:对数函数的最值与值域问题
【典例6-2】已知函数的最大值为2,则 .
【答案】6
【解析】因为函数由
与复合而成,
而在定义域上单调递增,所以当取最大值时,
函数取得最大值,
由二次函数的性质易知当时,,此时,
所以,解得.
【方法技巧】
对数函数的最值与值域问题通常利用对数函数的单调性解决.
题型六:对数函数的最值与值域问题
【变式6-1】若函数(且)的最小值为-4,则实数a的值为 .
【答案】
【解析】由题意知,,解得,
因为,
因为,则,又因为的最小值为-4,
则,所以,
即,得,
因为,所以.
题型六:对数函数的最值与值域问题
【变式6-2】已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【解析】(1)当时,函数恒有意义,
所以在上恒成立,
即在上恒成立.
令,,则,
所以在上单调递减,所以,所以.
又且,所以.
题型六:对数函数的最值与值域问题
【变式6-2】已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【解析】(2)函数在区间上有意义,则在上恒成立.
由(1)同理可知,,
又函数在区间上为减函数,并且最大值为.
当时,为减函数,则且在上单调递增,
所以,即,故不存在这样的实数;
当时,为增函数,则且在上单调递减,
所以,即,故不存在这样的实数.
综上,不存在这样的实数,使得函数在区间上为减函数,且最大值为.
题型六:对数函数的最值与值域问题
【典例7-1】已知函数,若对任意都有,则实数a的取值范围是( )
A. B. C. D.
【答案】D
【解析】因为若对任意,都有,
所以对任意,都有,
令,
则在上单调递增.
首先.
题型七:对数函数中的恒成立问题
【典例7-1】已知函数,若对任意都有,则实数a的取值范围是( )
A. B. C. D.
因为在上递增,所以在上递增.
当时,显然符合题意;
当时,令,
则在上递增,所以,则.
综上所述,,故D正确.
故选:D.
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
【答案】C
【解析】变形为:,
即在上恒成立,
若,此时在上单调递减,
,
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
而当时,,显然不合题意;
当时,画出两个函数的图像,
要想满足在上恒成立,
只需,即,
解得:,综上:实数a的取值范围是.故选:C
题型七:对数函数中的恒成立问题
【典例7-2】若不等式在上恒成立,则实数a的取值范围为( )
A. B. C. D.
【方法技巧】
已知不等式能恒成立求参数值(取值范围)问题常用的方法:
(1)函数法:讨论参数范围,通常借助函数单调性求解;
(2)分离参数法:首先将参数分离,转化成求函数的最值或值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,再利用数形结合的方法来解决.
题型七:对数函数中的恒成立问题
【变式7-1】已知函数,且,若对任意的,存在,使得成立,则实数的取值范围是 .
【答案】
【解析】根据题意知,
因为,其图象开口向下,对称轴为,
所以当时,其最小值,
当时,,在上的最小值为,
则由得,
当时,,在上的最小值为,则时,无解,
故实数的取值范围为.
题型七:对数函数中的恒成立问题
【变式7-2】已知且,当时,,则的取值范围为 .
【答案】
【解析】当时,.
当时,成立.
当时,若成立,是减函数,是增函数,则,解得,所以.
综上,的取值范围为.
题型七:对数函数中的恒成立问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
【答案】B
【解析】由题意知,,
,
令,则,
又因为与互为反函数,
所以、分别与的的交点关于对称,
所以,即:,
又因为,,
所以由零点存在性定理可知,,
题型八:对数函数的综合问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
又因为,即,
所以,
对于A项,因为,,
所以,故A项错误;
对于B项,因为,所以,
又因为,,
所以,故B项正确;
题型八:对数函数的综合问题
【典例8-1】(2024·四川南充·模拟预测)函数的零点为,
函数的零点为,则下列结论正确的是( )
A. B. C. D.
对于C项,因为,,
所以,故C项错误;
对于D项,因为, ,,
所以,故D项错误.故选:B.
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
【答案】D
【解析】当时,,
由复合函数的单调性可知在上单调递减,
所以;
当时,,
因为在上单调递增,为增函数,
所以在上单调递增,
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
又在上为增函数,所以在单调递增,
所以.
综上,在上恒成立,当且仅当时取等号.
所以不等式,
解得且且,即原不等式的解集为.
故选:D
题型八:对数函数的综合问题
【典例8-2】(2024·云南·二模)已知函数的定义域为,且
若,则的取值范围为( )
A. B.
C. D.
【方法技巧】
对数函数常与其他函数形成复合函数问题,解题时要清楚复合的层次,外层是对数函数还是内层是对数函数,其次如果涉及到定义域、值域、奇偶性、单调性等问题,则要按复合函数的性质规律求解.
题型八:对数函数的综合问题
【变式8-1】设定义域为R的函数,若关于x的方程有8个不同的实根,到实数b的取值范围是 .
【答案】
【解析】由题设,的图象如图所示:
令,则化为
,∴要使原方程有8个不同实根,
则有2个不同的实根且两根、,
题型八:对数函数的综合问题
【变式8-1】设定义域为R的函数,若关于x的方程有8个不同的实根,到实数b的取值范围是 .
∴,可得,
又在上递减,在上递增,且,
即,综上,.
题型八:对数函数的综合问题
04
真题练习·命题洞见
05
课本典例·高考素材
1.我们可以把看作每天的"进步”率都是1%,一年后是;而把看作每天的“落后”率都是1%,一年后是.利用计算工具计算并回答下列问题:
(1)一年后“进步”的是“落后”的多少倍?
(2)大约经过多少天后“进步”的分别是“落后”的10倍、100倍、1000倍?
【解析】(1).
∴一年后“进步”的大约是“落后”的倍
(2)由得,
∴大约经过天“进步”的是“落后”的倍.
由得.
∴大约经过天“进步”的是“落后”的倍.
由得解得
∴大约经过天“进步”的是“落后”的倍.
3.已知, , ,求实数a的取值范围.
【解析】解:,
当时成立;
②当时,解得.
又,
∴a的取值范围是.
06
易错分析·答题模板
答题模板:对数型复合函数的单调问题
1、模板解决思路
判断复合函数单调性的原则是“同增异减”.
2、模板解决步骤
第一步:求函数的定义域.
第二步:将函数分解成内层函数和外层函数.
第三步:判断内层函数和外层函数的单调性.
第四步:根据“同增异减”的原则确定复合函数的单调性.
【典例1】若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
【典例2】已知函数在上单调递减,则实数a的取值范围为( )
A. B. C. D.
B
A
感谢观看
THANK YOU
同课章节目录
