3.1 第3课时代数式的值 教案 2025-2026学年数学鲁教版(五四学制)六年级上册
文档属性
| 名称 | 3.1 第3课时代数式的值 教案 2025-2026学年数学鲁教版(五四学制)六年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 78.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 21:36:33 | ||
图片预览

文档简介
第3课时 代数式的值
会把具体数代入代数式进行计算.
1.在具体情境中,能求出代数式的值,并解释它的实际意义.
2.在代数式求值过程中,初步感受函数的对应思想.
3.感受字母取值的变化与代数式的值的变化之间的联系,能利用代数式的值推断一些代数式所反映的规律.
重点:正确计算代数式的值.
难点:理清“数值转换机”所设定代数式的运算顺序;感受代数式值的变化趋势并会进行预测、推断代数式所反映的规律.
重视“数值转换机”在教学中的作用,从“顺向”计算与“逆向分析”两个角度展开探讨,也可让学生自行设计类似的程序,帮助学生初步感受函数的对应思想,同时从代数式值的变化去感受一些代数式本身的变化规律,进一步理解代数式的意义和作用.
(一)情境导入
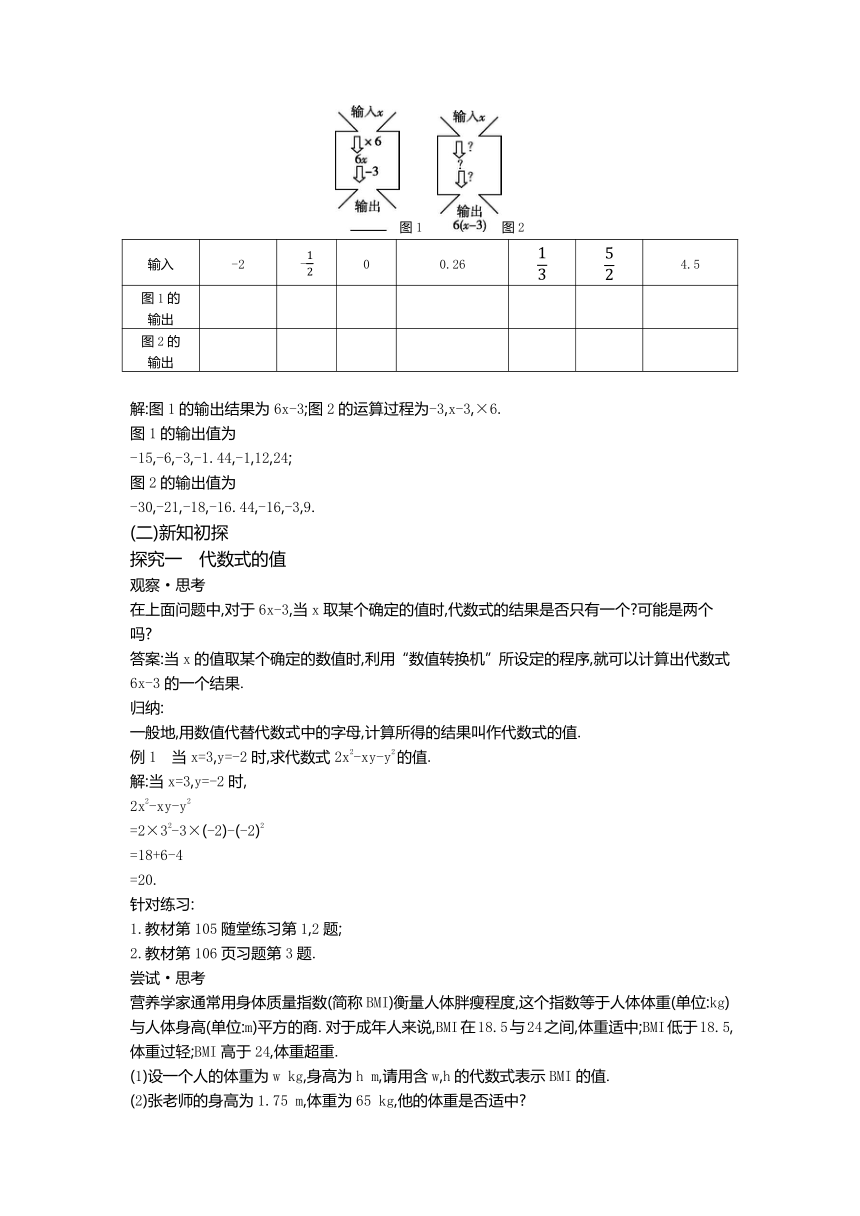
在计算机上可以设置运算程序,输入一组数据,计算机就会呈现运算结果,就好像一个“数值转换机”.
下面是一组“数值转换机”,请填写下表,写出图1的输出结果;写出图2的运算过程.
图1 图2
输入 -2 - 0 0.26 4.5
图1的 输出
图2的 输出
解:图1的输出结果为6x-3;图2的运算过程为-3,x-3,×6.
图1的输出值为
-15,-6,-3,-1.44,-1,12,24;
图2的输出值为
-30,-21,-18,-16.44,-16,-3,9.
(二)新知初探
探究一 代数式的值
观察·思考
在上面问题中,对于6x-3,当x取某个确定的值时,代数式的结果是否只有一个 可能是两个吗
答案:当x的值取某个确定的数值时,利用“数值转换机”所设定的程序,就可以计算出代数式6x-3的一个结果.
归纳:
一般地,用数值代替代数式中的字母,计算所得的结果叫作代数式的值.
例1 当x=3,y=-2时,求代数式2x2-xy-y2的值.
解:当x=3,y=-2时,
2x2-xy-y2
=2×32-3×(-2)-(-2)2
=18+6-4
=20.
针对练习:
1.教材第105随堂练习第1,2题;
2.教材第106页习题第3题.
尝试·思考
营养学家通常用身体质量指数(简称BMI)衡量人体胖瘦程度,这个指数等于人体体重(单位:kg)与人体身高(单位:m)平方的商.对于成年人来说,BMI在18.5与24之间,体重适中;BMI低于18.5,体重过轻;BMI高于24,体重超重.
(1)设一个人的体重为w kg,身高为h m,请用含w,h的代数式表示BMI的值.
(2)张老师的身高为1.75 m,体重为65 kg,他的体重是否适中
(3)BMI值对未成年人的胖瘦程度也有一定参考意义,请用上面的代数式计算你的BMI值,判断自己的体重是否适中.
解:(1).
(2)把h=1.75,w=65代入,得=≈21.22.
而18.5<21.22<24,因此他的身体适中.
(3)根据自己的身高与体重计算即可.
[方法归纳] 代数式求值的三种类型:
(1)直接代入求值
用具体数值代替代数式中的字母,按照代数式中的运算顺序计算.
(2)整体代入求值
根据代数式的特点,整体代入求得代数式的值,一般分直接整体代入与变形后整体代入.
(3)数值转化机求值
按指定程序代入计算.
任务一 意图说明
由数值转换机的情境切入课题,引出代数式的值的概念,并通过实例加以巩固.“数值转换机”事实上就是一个程序或算法,它可以直观形象地体现字母取值的变化与代数式的值的变化之间的对应关系,从而初步渗透函数的思想.
探究二 利用代数式的值推断一些代数式所反映的规律
观察·思考
填写下表,并观察5n+6和n2这两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
n2
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值如何变化
(2)估计一下,哪个代数式的值先超过100
解:填表:
第一行依次填:11,16,21,26,31,36,41,46;
第二行依次填:1,4,9,16,25,36,49,64.
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值逐渐增大.
(2)n2的值先超过100.
针对训练:教材第106页随堂练习第3题.
任务二 意图说明
代数式求值的重点在于在求值过程中进一步理解代数式的意义和作用,而不是单纯的符号计算.此问题的设计旨在说明根据代数式值的变化趋势还可以预测、推断代数式所反映的规律.问题(1)意在引导学生观察字母取值的变化与代数式的值的变化之间的联系;问题(2)意在引导学生发现“两个代数式”的值在变化中的关系(后者比前者增长得快).
(三)当堂达标(要求:限时5分钟,独立完成)
见课件
(四)课堂小结
见课件
(五)板书设计
字母表示数以后,使“数式”变成了“代数式”,当给出代数式中的字母所代表的具体的数以后,“代数式”又转化为“数式”,而这个“数式”的运算结果就是代数式的值.因此,根据所给代数式求代数式的值是一个由一般(式)到特殊(数)的问题.当给出代数式中的字母所代表的一个确定的数时,代数式也就表示一个确定的数.也就是说,代数式的值是由它里面的字母所取的值确定的.懂得这一点,不仅使学生能进一步理解代数式的意义和作用,巩固和熟练掌握有理数的四则运算,而且也为运用公式解决实际问题,以及今后进一步学习函数知识打下基础.由于本节知识整体难度不大,学生掌握知识的情况与课堂活动表现都很好.
会把具体数代入代数式进行计算.
1.在具体情境中,能求出代数式的值,并解释它的实际意义.
2.在代数式求值过程中,初步感受函数的对应思想.
3.感受字母取值的变化与代数式的值的变化之间的联系,能利用代数式的值推断一些代数式所反映的规律.
重点:正确计算代数式的值.
难点:理清“数值转换机”所设定代数式的运算顺序;感受代数式值的变化趋势并会进行预测、推断代数式所反映的规律.
重视“数值转换机”在教学中的作用,从“顺向”计算与“逆向分析”两个角度展开探讨,也可让学生自行设计类似的程序,帮助学生初步感受函数的对应思想,同时从代数式值的变化去感受一些代数式本身的变化规律,进一步理解代数式的意义和作用.
(一)情境导入
在计算机上可以设置运算程序,输入一组数据,计算机就会呈现运算结果,就好像一个“数值转换机”.
下面是一组“数值转换机”,请填写下表,写出图1的输出结果;写出图2的运算过程.
图1 图2
输入 -2 - 0 0.26 4.5
图1的 输出
图2的 输出
解:图1的输出结果为6x-3;图2的运算过程为-3,x-3,×6.
图1的输出值为
-15,-6,-3,-1.44,-1,12,24;
图2的输出值为
-30,-21,-18,-16.44,-16,-3,9.
(二)新知初探
探究一 代数式的值
观察·思考
在上面问题中,对于6x-3,当x取某个确定的值时,代数式的结果是否只有一个 可能是两个吗
答案:当x的值取某个确定的数值时,利用“数值转换机”所设定的程序,就可以计算出代数式6x-3的一个结果.
归纳:
一般地,用数值代替代数式中的字母,计算所得的结果叫作代数式的值.
例1 当x=3,y=-2时,求代数式2x2-xy-y2的值.
解:当x=3,y=-2时,
2x2-xy-y2
=2×32-3×(-2)-(-2)2
=18+6-4
=20.
针对练习:
1.教材第105随堂练习第1,2题;
2.教材第106页习题第3题.
尝试·思考
营养学家通常用身体质量指数(简称BMI)衡量人体胖瘦程度,这个指数等于人体体重(单位:kg)与人体身高(单位:m)平方的商.对于成年人来说,BMI在18.5与24之间,体重适中;BMI低于18.5,体重过轻;BMI高于24,体重超重.
(1)设一个人的体重为w kg,身高为h m,请用含w,h的代数式表示BMI的值.
(2)张老师的身高为1.75 m,体重为65 kg,他的体重是否适中
(3)BMI值对未成年人的胖瘦程度也有一定参考意义,请用上面的代数式计算你的BMI值,判断自己的体重是否适中.
解:(1).
(2)把h=1.75,w=65代入,得=≈21.22.
而18.5<21.22<24,因此他的身体适中.
(3)根据自己的身高与体重计算即可.
[方法归纳] 代数式求值的三种类型:
(1)直接代入求值
用具体数值代替代数式中的字母,按照代数式中的运算顺序计算.
(2)整体代入求值
根据代数式的特点,整体代入求得代数式的值,一般分直接整体代入与变形后整体代入.
(3)数值转化机求值
按指定程序代入计算.
任务一 意图说明
由数值转换机的情境切入课题,引出代数式的值的概念,并通过实例加以巩固.“数值转换机”事实上就是一个程序或算法,它可以直观形象地体现字母取值的变化与代数式的值的变化之间的对应关系,从而初步渗透函数的思想.
探究二 利用代数式的值推断一些代数式所反映的规律
观察·思考
填写下表,并观察5n+6和n2这两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
n2
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值如何变化
(2)估计一下,哪个代数式的值先超过100
解:填表:
第一行依次填:11,16,21,26,31,36,41,46;
第二行依次填:1,4,9,16,25,36,49,64.
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值逐渐增大.
(2)n2的值先超过100.
针对训练:教材第106页随堂练习第3题.
任务二 意图说明
代数式求值的重点在于在求值过程中进一步理解代数式的意义和作用,而不是单纯的符号计算.此问题的设计旨在说明根据代数式值的变化趋势还可以预测、推断代数式所反映的规律.问题(1)意在引导学生观察字母取值的变化与代数式的值的变化之间的联系;问题(2)意在引导学生发现“两个代数式”的值在变化中的关系(后者比前者增长得快).
(三)当堂达标(要求:限时5分钟,独立完成)
见课件
(四)课堂小结
见课件
(五)板书设计
字母表示数以后,使“数式”变成了“代数式”,当给出代数式中的字母所代表的具体的数以后,“代数式”又转化为“数式”,而这个“数式”的运算结果就是代数式的值.因此,根据所给代数式求代数式的值是一个由一般(式)到特殊(数)的问题.当给出代数式中的字母所代表的一个确定的数时,代数式也就表示一个确定的数.也就是说,代数式的值是由它里面的字母所取的值确定的.懂得这一点,不仅使学生能进一步理解代数式的意义和作用,巩固和熟练掌握有理数的四则运算,而且也为运用公式解决实际问题,以及今后进一步学习函数知识打下基础.由于本节知识整体难度不大,学生掌握知识的情况与课堂活动表现都很好.
同课章节目录
