北师大版2025—2026学年八年级上册数学开学测试模拟试卷(含答案)
文档属性
| 名称 | 北师大版2025—2026学年八年级上册数学开学测试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 905.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 20:55:00 | ||
图片预览


文档简介
北师大版2025—2026学年八年级上册数学开学测试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下面图形不是轴对称图形的是( )
A.线段 B.直角三角形 C.正方形 D.角
2.若,则( )
A.15 B.75 C.125 D.150
3.氢是一种气体元素,它是已知元素中最“轻”的,氢原子的直径为.则数字“”用科学记数法表示为( )
A. B. C. D.
4.一个书架上有三本书,分别是语文、数学、历史,从中随机抽取一本,抽到数学书的概率是( )
A. B. C. D.
5.按一定规律排列的单项式:,,,,…,则第6个单项式为( )
A. B. C. D.
6.以下事件是随机事件的是( )
A.太阳从西方升起
B.平面内画一个三角形,其内角和是
C.掷两枚质地均匀的骰子,朝上的面点数之和为1
D.掷一枚质地均匀的图钉,落地后钉尖朝上
7.有同学预测“小明在校初一乒乓球赛的决赛夺冠的可能性是”.则下列理解最合理的是( )
A.小明夺冠的可能性较大 B.小明夺冠的可能性较小
C.小明肯定会赢 D.若决赛赛10局,他一定会赢8局
8.已知,,则的值为( )
A.10 B.11 C.12 D.13
9.如图,将直尺与含角的直角三角板叠在一起,若,则的度数为( )
B.
C. D.
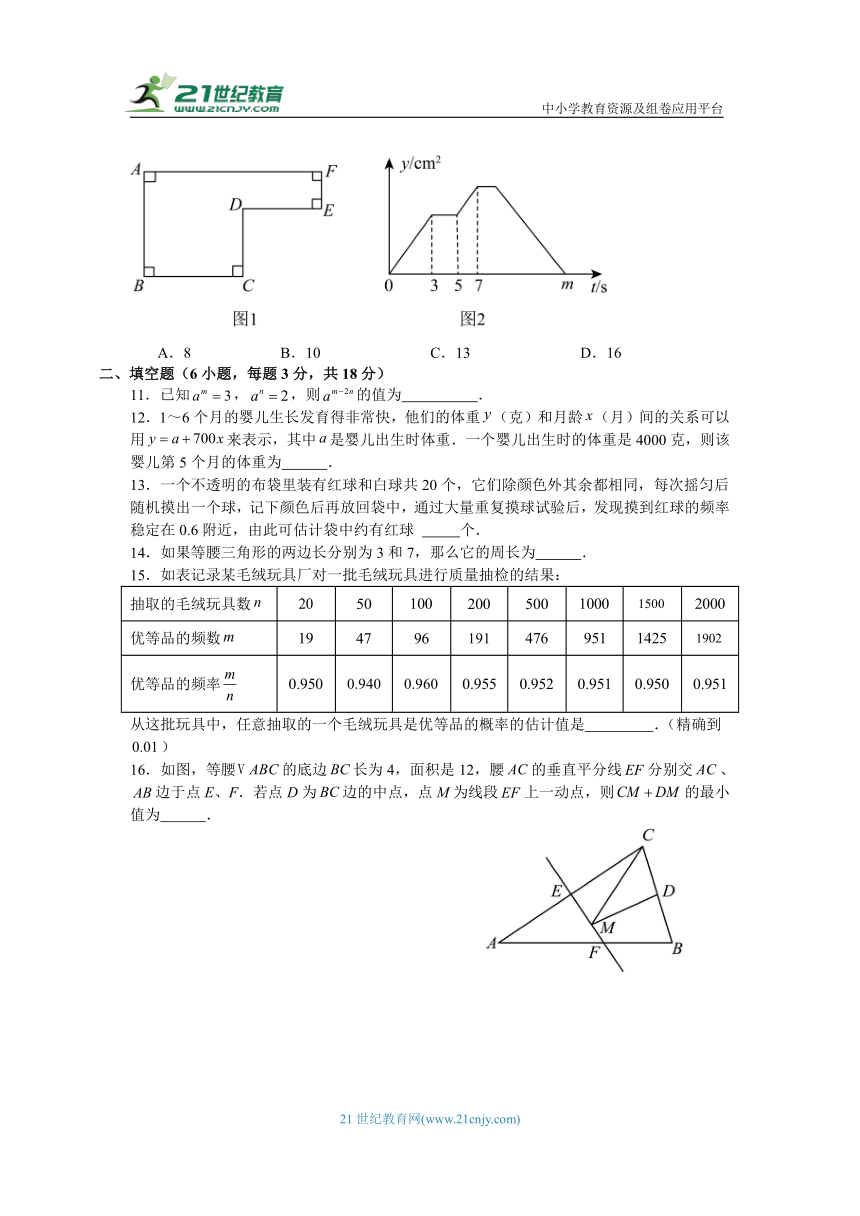
10.已知动点P以2cm/s的速度沿图1所示的边框按的路径运动,的面积与运动时间t(s)的关系如图2所示,若,则m的值为( )
A.8 B.10 C.13 D.16
二、填空题(6小题,每题3分,共18分)
11.已知,,则的值为 .
12.1~6个月的婴儿生长发育得非常快,他们的体重(克)和月龄(月)间的关系可以用来表示,其中是婴儿出生时体重.一个婴儿出生时的体重是4000克,则该婴儿第5个月的体重为 .
13.一个不透明的布袋里装有红球和白球共20个,它们除颜色外其余都相同,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.6附近,由此可估计袋中约有红球 个.
14.如果等腰三角形的两边长分别为3和7,那么它的周长为 .
15.如表记录某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果:
抽取的毛绒玩具数
优等品的频数
优等品的频率
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到)
16.如图,等腰的底边长为4,面积是12,腰的垂直平分线分别交、边于点E、F.若点D为边的中点,点M为线段上一动点,则的最小值为 .
第II卷
北师大版2025—2026学年八年级上册数学开学测试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中x=2,y=-1.
18.如图,△ABC中, BE是△ABC的角平分线,DE∥BC, 交AB于点D.若∠A=65°,∠BEC=95°,求∠BED的度数.
19.计算:
20.某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.
(1)他获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
(3)若要让获得20元购物券的概率变为,则转盘的颜色部分怎样修改?(直接写出修改方案即可).
21.如图,在中,,延长至点,使,过点作,使,连接.
(1)求证:;
(2)若,,求的长.
22.如图,ABC是格点三角形.
(1)在图中作出ABC关于直线l对称的(要求:A与,B与,C与相对应);
(2)在(1)的结果下,连接,,则的面积是______;
(3)在对称轴上有一点P,当PBC的周长最小时,P点在什么位置,在图中标出P点(保留作图痕迹).
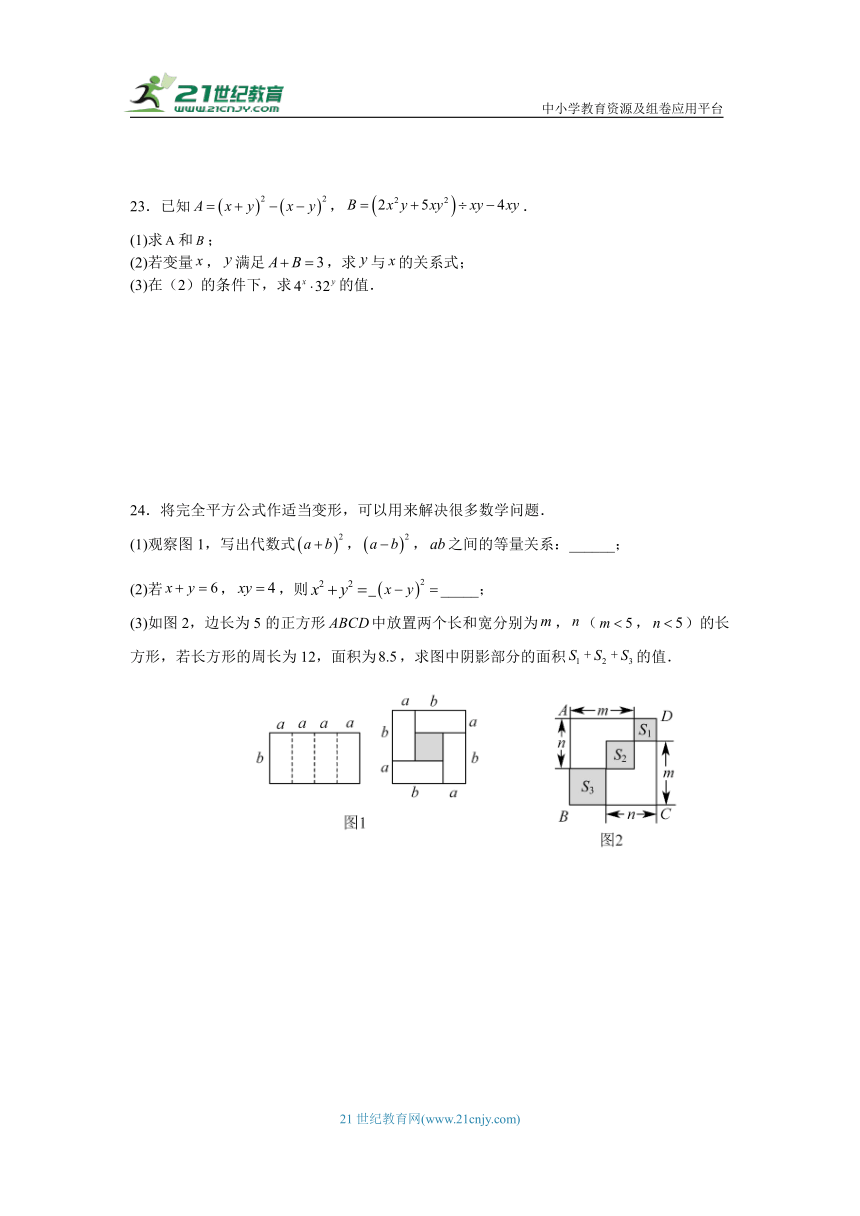
23.已知,.
(1)求和;
(2)若变量,满足,求与的关系式;
(3)在(2)的条件下,求的值.
24.将完全平方公式作适当变形,可以用来解决很多数学问题.
(1)观察图1,写出代数式,,之间的等量关系:______;
(2)若,,则 _____;
(3)如图2,边长为5的正方形中放置两个长和宽分别为,(,)的长方形,若长方形的周长为12,面积为,求图中阴影部分的面积的值.
25.如图:在△ABC 中,∠BAC=110°,AC=AB,射线 AD、AE 的夹角为 55°,过点 B 作BF⊥AD 于点 F,直线 BF 交 AE 于点 G,连接 CG.
(1)如图 1,若射线 AD、AE 都在∠BAC 的内部,且点 B 与点 B′关于 AD 对称,求证:CG=B'G;
(2)如图 2,若射线 AD 在∠BAC 的内部,射线 AE 在∠BAC 的外部,其他条件不变,求证:CG=BG﹣2GF;
(3)如图 3,若射线 AD、AE 都在∠BAC 的外部,其他条件不变,若 CG= GF,AF=4,S△ABG=12,求 BF 的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D B D D A C B C
二、填空题
11.【解】解:∵,,
∴.
故答案为:.
12.【解】解:由题意得:,,
克,
故答案为:7500克
13.【解】解:∵发现摸到红球的频率稳定在0.6附近,
∴摸到红球的概率约为0.6.
设袋中约有红球x个,
∴,解得:x=12
故答案为:12
14.【解】解:若3为腰长,7为底边长,
∵,
∴三角形不存在,
若7为腰长,3为底边长,则符合三角形的两边之各大于第三边,
∴这个三角形的周长,
故答案为:.
15.【解】解:∵表格中优等品的频率大概在左右浮动
∴从这批毛绒玩具中,任意抽取一个毛绒玩具是优等品的概率的估计值是,
故答案为.
16.【解】解:连接,,
∵是等腰三角形,点D是边的中点,
∴,
∵是线段的垂直平分线,
∴,
∴,
∴与的交点为点时最小,且的最小值为的长,
∵在中,,,
∴,
解得:,
∴的最小值为6.
故答案为:6.
三、解答题
17.【解】解:[(2x+y)2-(2x-y)(2x+y)]÷(2y),
=[4x2+4xy+y2-4x2+y2]÷(2y),
=(4xy+2y2)÷(2y),
=2x+y,
当x=2,y=-1时,
原式=2×2+(-1)=3.
18.【解】∵∠BEC是△ABE的外角,
∴∠BEC =∠A+∠ABE.
∵∠A = 65°,∠BEC = 95°,
∴∠ABE =∠BEC-∠A = 95°-65° =30°
∵BE是△ABC的角平分线,
∴∠ABE =∠EBC.
∵DE∥BC,
∴∠DEB =∠EBC
∴∠DEB =∠EBC =∠ABE = 30°.
19.【解】解:
=
=
20.【解】解:(1)∵共有20种等可能事件,其中满足条件的有11种,
∴(中奖),
(2)由题意得:共有20种等可能结果,其中获100元购物券的有2种,获得50元购物券的有4种,获得20元购物券的有5种,
∴(获得100元);
(获得50元);
(获得20元);
(3)因为要让获得20元购物券的概率变为,所以直接将3个无色扇形涂为黄色.
21.【解】(1)∵,,
∴,
∴,
∵,,
∴;
(2)∵,
∴,
∵,
∴,
∵,
∴.
22.【解】(1)如图所示,即为所求;
(2)△ABB1的面积是×4×2=4,
故答案为:4;
(3)如图所示,连接B1C,与直线l的交点P即为所求,
PBC的周长=BC+CP+BP=BC+CP+B1P≥BC+B1C
∴当点C、P和点B1三点共线时,PBC的周长最小,
所以点P即为所求.
23.【解】(1)解:
(2)解:∵,
∴,
∴;
(3)解:∵,
∴.
24.【解】(1)解:图1中左边一幅图空白部分面积可以表示为4个小长方形面积,即;
图1中右边一幅图空白部分面积可以表示大正方形面积减去中间阴影部分正方形面积,即;
∴,
故答案为:;
(2)解:∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
故答案为:28,20;
(3)解:如图所示,
由题意得,,
∵长方形的周长为12,面积为,
∴,
∴,
∴
.
25.【解】(1)证明:如图1,连接,
∵B,关于AD对称,
∴被AD垂直平分,
∴,
∵,
,
,
,
,
,
,
,
,
,
,
,
,
.
(2)证明:如图2,在FB上截取,连接,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)解:如图3,延长BF至点,使,连接,
,
,
,
,
,
,
,
,
,
,
∴,
∵,
∴,
,
,AF=4,
,
,
∴BG=6,
设GF=x,
,
,
∵CG=G'B ,
,
∴x=8,
∴BF=8+6=14.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下面图形不是轴对称图形的是( )
A.线段 B.直角三角形 C.正方形 D.角
2.若,则( )
A.15 B.75 C.125 D.150
3.氢是一种气体元素,它是已知元素中最“轻”的,氢原子的直径为.则数字“”用科学记数法表示为( )
A. B. C. D.
4.一个书架上有三本书,分别是语文、数学、历史,从中随机抽取一本,抽到数学书的概率是( )
A. B. C. D.
5.按一定规律排列的单项式:,,,,…,则第6个单项式为( )
A. B. C. D.
6.以下事件是随机事件的是( )
A.太阳从西方升起
B.平面内画一个三角形,其内角和是
C.掷两枚质地均匀的骰子,朝上的面点数之和为1
D.掷一枚质地均匀的图钉,落地后钉尖朝上
7.有同学预测“小明在校初一乒乓球赛的决赛夺冠的可能性是”.则下列理解最合理的是( )
A.小明夺冠的可能性较大 B.小明夺冠的可能性较小
C.小明肯定会赢 D.若决赛赛10局,他一定会赢8局
8.已知,,则的值为( )
A.10 B.11 C.12 D.13
9.如图,将直尺与含角的直角三角板叠在一起,若,则的度数为( )
B.
C. D.
10.已知动点P以2cm/s的速度沿图1所示的边框按的路径运动,的面积与运动时间t(s)的关系如图2所示,若,则m的值为( )
A.8 B.10 C.13 D.16
二、填空题(6小题,每题3分,共18分)
11.已知,,则的值为 .
12.1~6个月的婴儿生长发育得非常快,他们的体重(克)和月龄(月)间的关系可以用来表示,其中是婴儿出生时体重.一个婴儿出生时的体重是4000克,则该婴儿第5个月的体重为 .
13.一个不透明的布袋里装有红球和白球共20个,它们除颜色外其余都相同,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.6附近,由此可估计袋中约有红球 个.
14.如果等腰三角形的两边长分别为3和7,那么它的周长为 .
15.如表记录某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果:
抽取的毛绒玩具数
优等品的频数
优等品的频率
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到)
16.如图,等腰的底边长为4,面积是12,腰的垂直平分线分别交、边于点E、F.若点D为边的中点,点M为线段上一动点,则的最小值为 .
第II卷
北师大版2025—2026学年八年级上册数学开学测试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中x=2,y=-1.
18.如图,△ABC中, BE是△ABC的角平分线,DE∥BC, 交AB于点D.若∠A=65°,∠BEC=95°,求∠BED的度数.
19.计算:
20.某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.
(1)他获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
(3)若要让获得20元购物券的概率变为,则转盘的颜色部分怎样修改?(直接写出修改方案即可).
21.如图,在中,,延长至点,使,过点作,使,连接.
(1)求证:;
(2)若,,求的长.
22.如图,ABC是格点三角形.
(1)在图中作出ABC关于直线l对称的(要求:A与,B与,C与相对应);
(2)在(1)的结果下,连接,,则的面积是______;
(3)在对称轴上有一点P,当PBC的周长最小时,P点在什么位置,在图中标出P点(保留作图痕迹).
23.已知,.
(1)求和;
(2)若变量,满足,求与的关系式;
(3)在(2)的条件下,求的值.
24.将完全平方公式作适当变形,可以用来解决很多数学问题.
(1)观察图1,写出代数式,,之间的等量关系:______;
(2)若,,则 _____;
(3)如图2,边长为5的正方形中放置两个长和宽分别为,(,)的长方形,若长方形的周长为12,面积为,求图中阴影部分的面积的值.
25.如图:在△ABC 中,∠BAC=110°,AC=AB,射线 AD、AE 的夹角为 55°,过点 B 作BF⊥AD 于点 F,直线 BF 交 AE 于点 G,连接 CG.
(1)如图 1,若射线 AD、AE 都在∠BAC 的内部,且点 B 与点 B′关于 AD 对称,求证:CG=B'G;
(2)如图 2,若射线 AD 在∠BAC 的内部,射线 AE 在∠BAC 的外部,其他条件不变,求证:CG=BG﹣2GF;
(3)如图 3,若射线 AD、AE 都在∠BAC 的外部,其他条件不变,若 CG= GF,AF=4,S△ABG=12,求 BF 的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D B D D A C B C
二、填空题
11.【解】解:∵,,
∴.
故答案为:.
12.【解】解:由题意得:,,
克,
故答案为:7500克
13.【解】解:∵发现摸到红球的频率稳定在0.6附近,
∴摸到红球的概率约为0.6.
设袋中约有红球x个,
∴,解得:x=12
故答案为:12
14.【解】解:若3为腰长,7为底边长,
∵,
∴三角形不存在,
若7为腰长,3为底边长,则符合三角形的两边之各大于第三边,
∴这个三角形的周长,
故答案为:.
15.【解】解:∵表格中优等品的频率大概在左右浮动
∴从这批毛绒玩具中,任意抽取一个毛绒玩具是优等品的概率的估计值是,
故答案为.
16.【解】解:连接,,
∵是等腰三角形,点D是边的中点,
∴,
∵是线段的垂直平分线,
∴,
∴,
∴与的交点为点时最小,且的最小值为的长,
∵在中,,,
∴,
解得:,
∴的最小值为6.
故答案为:6.
三、解答题
17.【解】解:[(2x+y)2-(2x-y)(2x+y)]÷(2y),
=[4x2+4xy+y2-4x2+y2]÷(2y),
=(4xy+2y2)÷(2y),
=2x+y,
当x=2,y=-1时,
原式=2×2+(-1)=3.
18.【解】∵∠BEC是△ABE的外角,
∴∠BEC =∠A+∠ABE.
∵∠A = 65°,∠BEC = 95°,
∴∠ABE =∠BEC-∠A = 95°-65° =30°
∵BE是△ABC的角平分线,
∴∠ABE =∠EBC.
∵DE∥BC,
∴∠DEB =∠EBC
∴∠DEB =∠EBC =∠ABE = 30°.
19.【解】解:
=
=
20.【解】解:(1)∵共有20种等可能事件,其中满足条件的有11种,
∴(中奖),
(2)由题意得:共有20种等可能结果,其中获100元购物券的有2种,获得50元购物券的有4种,获得20元购物券的有5种,
∴(获得100元);
(获得50元);
(获得20元);
(3)因为要让获得20元购物券的概率变为,所以直接将3个无色扇形涂为黄色.
21.【解】(1)∵,,
∴,
∴,
∵,,
∴;
(2)∵,
∴,
∵,
∴,
∵,
∴.
22.【解】(1)如图所示,即为所求;
(2)△ABB1的面积是×4×2=4,
故答案为:4;
(3)如图所示,连接B1C,与直线l的交点P即为所求,
PBC的周长=BC+CP+BP=BC+CP+B1P≥BC+B1C
∴当点C、P和点B1三点共线时,PBC的周长最小,
所以点P即为所求.
23.【解】(1)解:
(2)解:∵,
∴,
∴;
(3)解:∵,
∴.
24.【解】(1)解:图1中左边一幅图空白部分面积可以表示为4个小长方形面积,即;
图1中右边一幅图空白部分面积可以表示大正方形面积减去中间阴影部分正方形面积,即;
∴,
故答案为:;
(2)解:∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
故答案为:28,20;
(3)解:如图所示,
由题意得,,
∵长方形的周长为12,面积为,
∴,
∴,
∴
.
25.【解】(1)证明:如图1,连接,
∵B,关于AD对称,
∴被AD垂直平分,
∴,
∵,
,
,
,
,
,
,
,
,
,
,
,
,
.
(2)证明:如图2,在FB上截取,连接,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)解:如图3,延长BF至点,使,连接,
,
,
,
,
,
,
,
,
,
,
∴,
∵,
∴,
,
,AF=4,
,
,
∴BG=6,
设GF=x,
,
,
∵CG=G'B ,
,
∴x=8,
∴BF=8+6=14.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
