2.3 整式的概念 ( 第1课时) 整式的概念 课件 (27张PPT) 2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 2.3 整式的概念 ( 第1课时) 整式的概念 课件 (27张PPT) 2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 16:24:38 | ||
图片预览








文档简介
(共27张PPT)
2.3 整式的概念
第1课时 整式的概念
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
港珠澳大桥是集主桥、海底隧道和人工岛为一体的世界上最长的跨海大桥.一辆汽车从香港口岸行驶到东人工岛的平均速度为96km/h,在海底隧道和主桥上行驶的平均速度分别为72 km/h和92 km/h.请根据这些数据回答:
汽车在主桥上行驶th的路程是多少千米
观察所列式子包含什么运算,有什么特点.
壹
92t
新知初探
贰
新知初探
探究一 单项式的相关概念
用含有字母的式子填空,并观察特点:
(1)以8km/h的平均速度行走th的路程是 ;
(2)半径为r的圆的面积是 ;
(3)底面是边长为x的正方形,高为y的长方体的体积是 .
(4)铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠 笔的单价是 元.
2.5x
贰
8t
π
问题
问题1 上述代数式中含有加减运算吗?只含哪些运算?
解:上述代数式中不含有加减运算,只含数与字母的幂的乘法运算.
问题2 单独一个字母是单项式吗?它的系数和次数分别是多少?
答:单独一个字母是单项式,它的系数是1,次数是1.
问题3 单项式书写注意哪些问题?
答:书写单项式时,一般数字写在前面,字母写在后边,字母顺序一般遵循英文字母表顺序.
问题4 , ,-16x哪些是单项式 是单项式的写出其系数和次数.
答:-16x是单项式,其系数是﹣16,次数是1.
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积).
由数与字母及其幂的乘积组成的代数式叫作单项式,单独的一个数也可看作单项式,并约定一个不为0的数的其次数为0.
知识要点
例如:像 2024, x , 等是单项式.
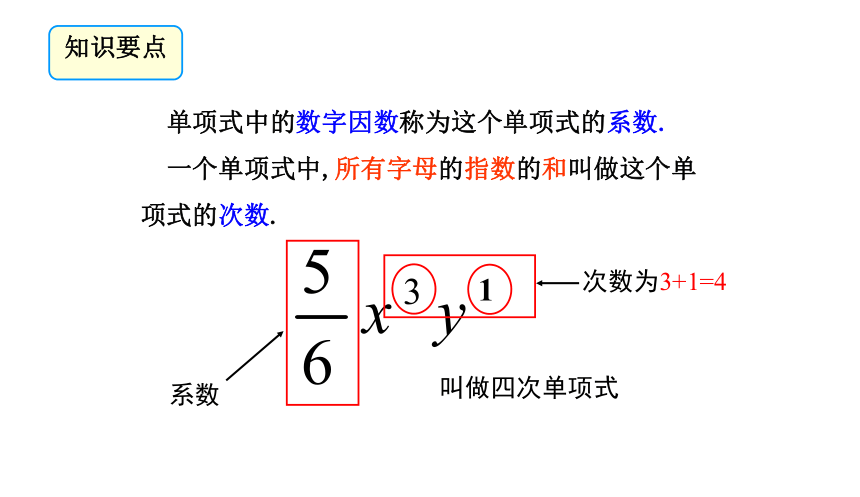
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
次数为3+1=4
叫做四次单项式
知识要点
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
方法总结:判断单项式的方法
例题讲解
例1.判断下列各式是否是单项式,如果不是,请简要说明理由;如果是,
请指出它的系数与次数.
(1) x+1;(2) ;(3)πr2;(4)- a2b.
解:(1) x+1不是单项式,因为代数式中出现了加法运算.
(2) 不是单项式,因为代数式中出现了数字与字母的除法运算.
(3)πr2是单项式,系数是π,次数是2;
(4)- a2b是单项式,系数是- ,次数是3.
新知初探
探究二 多项式的相关概念
1.图是由一个长方形和一个半圆组成,已知长方形的长为x,宽为y,半圆的直径为y.
(1)长方形的面积为 ;
(2)半圆的面积为 ;
(3)由长方形和半圆组成的图形的面积为 .
贰
xy
xy+π
问题 上述几个式子都是单项式吗 若不是单项式,它有什么共同特点
解:(1)(2)是单项式(3)不是单项式,它是两个多个单项式相加的形式.
2.如图三角尺的面积为 .
3.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
1.买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,那么买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
问题 上述几个式子分别是几个单项式的和组成 是哪几个单项式?每个单项式的次数是多少?系数是多少?
解:(1)是三个单项式的和,分别是3x、5y、2z,其次数分别是1,1,1,系数分别为3,5,2;
(2)是两个单项式的和,分别是ab、-π,次数分别是2,2,系数分别为、﹣π;
(3)是三个单项式的和,分别是、2x、18,其次数分别是2,1,0,系数为1,2.
(1)几个单项式的和叫作多项式.
(3) 多项式中不含字母的项次数为0.
(4)单项式和多项式统称整式.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
方法归纳
问题1 多项式中不含分母的项怎么定义?
答:不含分母的项叫作常数项.
问题2 多项式的次数怎么定义?
答:次数最高项的次数叫作多项式的次数.
问题3 一个多项式的最高次项一定只有一项吗?
答:一个多项式的最高次项可以不只一项.
问题
解:(1)2x-3的项是2x,-3,次数是1,常数项是-3;
(2)﹣+7x-4的项是-,7x,﹣4,次数是3,常数项是﹣4;
(3)3-5xy+-4x+6y-9的项是3,-5xy,,-4x,6y,-9,次数是2,常数项是-9.
例题讲解
例2.说出下列多项式的项,次数和常数项.
(1)2x-3;
(2)﹣+7x-4;
(3)3-5xy+-4x+6y-9.
例3.已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
变式
当堂达标
叁
1.下列式子中,是单项式的是( )
A. B. C.a2+3b3 D.
B
当堂达标
叁
2.下列各式中是整式的有( )
1-3x2,- x3, ,﹣ ,π+ a,0,-x2+y2-1.
A.7个 B.6个 C.5个 D.4个
B
4.有一块长为x m、宽为y m的长方形草坪,在草坪中间有一条宽为2 m的人行道,形状如图所示,则这块草坪的实际绿化面积
是 m2.
(xy-2y)
当堂达标
叁
3.若单项式-a2bm与-x3y4是次数相同的单项式,则m的值为 .
5.已知(a-1)x2ya+1是关于x,y的五次单项式,求这个单项式的系数.
解:由题意得:a+1+2=5,
解得:a=2,
则这个单项式的系数是a-1=1.
5
6.已知多项式a3+ ab4-am+1b-6是六次四项式,单项式2xy3n与该多项式的次数相同,求m2+n2的值.
解:依题意得m+1+1=6,1+3n=6,
则m=4,n= .
所以m2+n2=42+ = .
课堂小结
肆
课堂小结
1.单项式相关概念
(1)由数与字母及其幂的乘积组成的代数式,单独的一个数也看作单项式.
(2)单项式中的数叫作单项式系数,所有字母的指数的和叫作单项式的次数.
2.多项式相关概念
(1)几个单项式的和叫作多项式.
(2)多项式中的每个单项式叫作多项式的项,不含字母的项叫作常数项.次数最高的项的次数叫作多项式的次数.
肆
课后作业
基础题:1.课后练习 第 1,2题。
提高题:2.若-mx2y|n-3|是关于x,y的十次单项式,且系数是8,求m+n的值
谢
谢
2.3 整式的概念
第1课时 整式的概念
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
港珠澳大桥是集主桥、海底隧道和人工岛为一体的世界上最长的跨海大桥.一辆汽车从香港口岸行驶到东人工岛的平均速度为96km/h,在海底隧道和主桥上行驶的平均速度分别为72 km/h和92 km/h.请根据这些数据回答:
汽车在主桥上行驶th的路程是多少千米
观察所列式子包含什么运算,有什么特点.
壹
92t
新知初探
贰
新知初探
探究一 单项式的相关概念
用含有字母的式子填空,并观察特点:
(1)以8km/h的平均速度行走th的路程是 ;
(2)半径为r的圆的面积是 ;
(3)底面是边长为x的正方形,高为y的长方体的体积是 .
(4)铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠 笔的单价是 元.
2.5x
贰
8t
π
问题
问题1 上述代数式中含有加减运算吗?只含哪些运算?
解:上述代数式中不含有加减运算,只含数与字母的幂的乘法运算.
问题2 单独一个字母是单项式吗?它的系数和次数分别是多少?
答:单独一个字母是单项式,它的系数是1,次数是1.
问题3 单项式书写注意哪些问题?
答:书写单项式时,一般数字写在前面,字母写在后边,字母顺序一般遵循英文字母表顺序.
问题4 , ,-16x哪些是单项式 是单项式的写出其系数和次数.
答:-16x是单项式,其系数是﹣16,次数是1.
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积).
由数与字母及其幂的乘积组成的代数式叫作单项式,单独的一个数也可看作单项式,并约定一个不为0的数的其次数为0.
知识要点
例如:像 2024, x , 等是单项式.
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
次数为3+1=4
叫做四次单项式
知识要点
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
方法总结:判断单项式的方法
例题讲解
例1.判断下列各式是否是单项式,如果不是,请简要说明理由;如果是,
请指出它的系数与次数.
(1) x+1;(2) ;(3)πr2;(4)- a2b.
解:(1) x+1不是单项式,因为代数式中出现了加法运算.
(2) 不是单项式,因为代数式中出现了数字与字母的除法运算.
(3)πr2是单项式,系数是π,次数是2;
(4)- a2b是单项式,系数是- ,次数是3.
新知初探
探究二 多项式的相关概念
1.图是由一个长方形和一个半圆组成,已知长方形的长为x,宽为y,半圆的直径为y.
(1)长方形的面积为 ;
(2)半圆的面积为 ;
(3)由长方形和半圆组成的图形的面积为 .
贰
xy
xy+π
问题 上述几个式子都是单项式吗 若不是单项式,它有什么共同特点
解:(1)(2)是单项式(3)不是单项式,它是两个多个单项式相加的形式.
2.如图三角尺的面积为 .
3.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
1.买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,那么买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
问题 上述几个式子分别是几个单项式的和组成 是哪几个单项式?每个单项式的次数是多少?系数是多少?
解:(1)是三个单项式的和,分别是3x、5y、2z,其次数分别是1,1,1,系数分别为3,5,2;
(2)是两个单项式的和,分别是ab、-π,次数分别是2,2,系数分别为、﹣π;
(3)是三个单项式的和,分别是、2x、18,其次数分别是2,1,0,系数为1,2.
(1)几个单项式的和叫作多项式.
(3) 多项式中不含字母的项次数为0.
(4)单项式和多项式统称整式.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
方法归纳
问题1 多项式中不含分母的项怎么定义?
答:不含分母的项叫作常数项.
问题2 多项式的次数怎么定义?
答:次数最高项的次数叫作多项式的次数.
问题3 一个多项式的最高次项一定只有一项吗?
答:一个多项式的最高次项可以不只一项.
问题
解:(1)2x-3的项是2x,-3,次数是1,常数项是-3;
(2)﹣+7x-4的项是-,7x,﹣4,次数是3,常数项是﹣4;
(3)3-5xy+-4x+6y-9的项是3,-5xy,,-4x,6y,-9,次数是2,常数项是-9.
例题讲解
例2.说出下列多项式的项,次数和常数项.
(1)2x-3;
(2)﹣+7x-4;
(3)3-5xy+-4x+6y-9.
例3.已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
变式
当堂达标
叁
1.下列式子中,是单项式的是( )
A. B. C.a2+3b3 D.
B
当堂达标
叁
2.下列各式中是整式的有( )
1-3x2,- x3, ,﹣ ,π+ a,0,-x2+y2-1.
A.7个 B.6个 C.5个 D.4个
B
4.有一块长为x m、宽为y m的长方形草坪,在草坪中间有一条宽为2 m的人行道,形状如图所示,则这块草坪的实际绿化面积
是 m2.
(xy-2y)
当堂达标
叁
3.若单项式-a2bm与-x3y4是次数相同的单项式,则m的值为 .
5.已知(a-1)x2ya+1是关于x,y的五次单项式,求这个单项式的系数.
解:由题意得:a+1+2=5,
解得:a=2,
则这个单项式的系数是a-1=1.
5
6.已知多项式a3+ ab4-am+1b-6是六次四项式,单项式2xy3n与该多项式的次数相同,求m2+n2的值.
解:依题意得m+1+1=6,1+3n=6,
则m=4,n= .
所以m2+n2=42+ = .
课堂小结
肆
课堂小结
1.单项式相关概念
(1)由数与字母及其幂的乘积组成的代数式,单独的一个数也看作单项式.
(2)单项式中的数叫作单项式系数,所有字母的指数的和叫作单项式的次数.
2.多项式相关概念
(1)几个单项式的和叫作多项式.
(2)多项式中的每个单项式叫作多项式的项,不含字母的项叫作常数项.次数最高的项的次数叫作多项式的次数.
肆
课后作业
基础题:1.课后练习 第 1,2题。
提高题:2.若-mx2y|n-3|是关于x,y的十次单项式,且系数是8,求m+n的值
谢
谢
同课章节目录
