2.4 整式的加法与减法第2课时(共25张PPT) 2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 2.4 整式的加法与减法第2课时(共25张PPT) 2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 16:25:03 | ||
图片预览








文档简介
(共25张PPT)
2.4 整式的加法与减法
第2课时 整式加减的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
运用前面所学的知识填空:
小亮和小莹到希望小学去看望小同学,小亮买了10支钢笔和5本字典作为礼物;小莹买了6支钢笔、4本字典和2个文具盒作为礼物品.钢笔的售价为每支a元,字典的售价为每本b元,文具盒的售价为每个c元.
请你计算:(1)小亮花了 元;
小莹花了 元;小亮和小莹共花 元.
(2)小亮比小莹多花 元.
(10a+5b)
(6a+4b+2c)
(16a+9b+2c)
(4a+b-2c)
想一想:如何进行整式的加减运算?
壹
新知初探
贰
+ _ = .
新知初探
活动一 整式的加减
10a+b+10b+a=11a+11b=11(a+b)
合作探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
贰
做一做
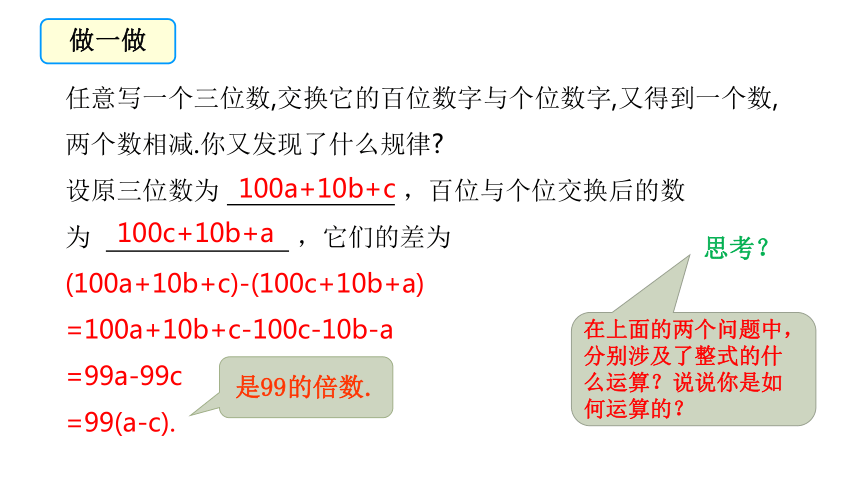
任意写一个三位数,交换它的百位数字与个位数字,又得到一个数,两个数相减.你又发现了什么规律
设原三位数为 ,百位与个位交换后的数为 ,它们的差为
(100a+10b+c)-(100c+10b+a)
=100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
做一做
100a+10b+c
100c+10b+a
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
是99的倍数.
思考?
几个整式相加减,如果有括号就先去括号,然后再合并同类项
归纳总结
例1.计算:
(3)-2()+(﹣4)
去括号
合并同类项
移项
解:(3)-2()+(﹣4)
=3-(2)﹣4
=3-2﹣4
=3-2
=[3+(-2)+(
=
去括号
探究二 例题讲解
问题 上述运算应用了什么运算律?
答:应用分配律、交换律和结合律.
问题 整式加减的实质是什么?
答:去括号、合并同类项.
[方法归纳]
(1)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算;
(2)整式加减实际上就是:去括号、合并同类项;
(3)运算结果,常将多项式的某个字母(如x)降幂(升幂)排列.
探究二 整式的加化简求值
例2. 计算:
(1)(4x -5xy+3y )-(3x +2y );
(2) [4×(-2) -5×(﹣2)×3+3×3 ]-[3×(-2) +2×3 ];
(3)[4×(﹣b) -5×(﹣b)×c+3×c ]-[3×(-b) +2×c ]
分析:将(2)与(1)进行比较,发现将(1)中的字母x,y分别用﹣2,3代入可得(2),于是(1)中的结果中的字母x,y分别用﹣2,3代入,即可得(2)的结果,类似地,可以求得(3)的计算结果.
探究二 整式的加化简求值
解:(1)(4x -5xy+3y )-(3x +2y )
=4x -5xy+3y -3x -2y
=x -5xy+y ;
(2)将等式①中的x用一2,y用3代入,则
[4×(-2) -5×(﹣2)×3+3×3 ]-[3×(-2) +2×3 ]
=(﹣2) -5×(﹣2)×3+3
=4+30+9
=43.
(去括号)
(合并同类项)
(代入化简后的式子)
探究二 整式的加减化简求值
(3)将等式①中的x用一b代人,则
[4×(﹣b) -5×(﹣b)×c+3×c ]-[3×(-b) +2×c ]
=(﹣b) -5×(﹣b)c+c
=b +5bc+c .
小结:
(1)多项式的重要性:
要将一个多项式经过计算得到的等式中的字母,用任意数或任意多项式代人,就可得到许多等式,这休现了多项式的重要性。
(2)多项式的化简求值
先把原多项式去括号、合并同类项,再把给定的条件代入化简后的式子进行计算.
等式中的字母可以用任意数会任意多项式代入
例3.做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
a
b
c
1.5a
2b
2c
探究三 整式加减的应用
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm2 )
解:小纸盒的表面积是( )cm2
2ab
+2bc
+2ca
大纸盒的表面积是( )cm2
6ab
+8bc
+ 6ca
整式加减解决实际问题的一般步骤:
⑴ 根据题意列代数式;
⑵ 去括号、合并同类项.;
⑶ 得出最后结果.
总结归纳
当堂达标
叁
当堂达标
1.化简2(x+ )- (3x-6)的结果是( )
A.3x+3 B.3x-3 C.x+3 D.x-3
2.多项式2x3-10x2+4x-1与多项式3x3-4x-5x2+3相加,合并后不含的项是( )
A.三次项 B.二次项 C.一次项 D.常数项
3.一个两位数,它的十位数字是a,个位数字是b,将这个两位数的个位数字和十位数字交换位置后得到一个新的两位数,求所得数与原数的和 (用含a,b的代数式表示).
C
C
叁
11(a+b)
4.先计算,2(-5x+x)+(3x-2x)-3(-x+7x), 再利用所得结果计算:
2[×-5×(﹣1)]+[3×(﹣1)×-2×(﹣1)]-3[(﹣1)3×-(﹣1)+7×(﹣1)].
解:2(-5x+x)+(3x-2x)-3(-x+7x)
=2-10x+2x+3x-2x-3+3x21x
=(2-3)-10)+3+3]x+[2+(-2)+(﹣21)]x
=--4x-21x
解:2[×-5×(﹣1)]+[3×(﹣1)×-2×(﹣1)]-3[(﹣1)3×-(﹣1)+7×(﹣1)
=--4×(﹣1)×-21×(﹣1)
=57
5.某校有A,B,C三个课外活动小组,A小组有学生(x+2y)名,B小组学生人数是A小组学生人数的3倍,C小组比A小组多3名学生,问A,B,C三个课外活动小组共有多少名学生
解:B小组学生人数为3(x+2y)名,C小组学生人数为[(x+2y)+3]名.
(x+2y)+3(x+2y)+(x+2y)+3=5(x+2y)+3
=(5x+10y+3)(名).
答:A,B,C三个课外活动小组共有(5x+10y+3)名学生.
课堂小结
肆
课堂小结
1.整式加减:
几个整式相加减,如果有括号就先去括号,然后再合并同类项.
2.化简求值时,一般先将整式进行化简,再把数值代入化简后的式子计算.
3.利用整式加减解决实际问题的一般步骤:
(1)根据题意列式;(2)去括号、合并同类项;(3)得出最后结果.
肆
课后作业
基础题:1.课后练习 第 1 题。
提高题:2.请学有余力的同学完成课后习题第4,5题
谢
谢
2.4 整式的加法与减法
第2课时 整式加减的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
运用前面所学的知识填空:
小亮和小莹到希望小学去看望小同学,小亮买了10支钢笔和5本字典作为礼物;小莹买了6支钢笔、4本字典和2个文具盒作为礼物品.钢笔的售价为每支a元,字典的售价为每本b元,文具盒的售价为每个c元.
请你计算:(1)小亮花了 元;
小莹花了 元;小亮和小莹共花 元.
(2)小亮比小莹多花 元.
(10a+5b)
(6a+4b+2c)
(16a+9b+2c)
(4a+b-2c)
想一想:如何进行整式的加减运算?
壹
新知初探
贰
+ _ = .
新知初探
活动一 整式的加减
10a+b+10b+a=11a+11b=11(a+b)
合作探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
贰
做一做
任意写一个三位数,交换它的百位数字与个位数字,又得到一个数,两个数相减.你又发现了什么规律
设原三位数为 ,百位与个位交换后的数为 ,它们的差为
(100a+10b+c)-(100c+10b+a)
=100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
做一做
100a+10b+c
100c+10b+a
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
是99的倍数.
思考?
几个整式相加减,如果有括号就先去括号,然后再合并同类项
归纳总结
例1.计算:
(3)-2()+(﹣4)
去括号
合并同类项
移项
解:(3)-2()+(﹣4)
=3-(2)﹣4
=3-2﹣4
=3-2
=[3+(-2)+(
=
去括号
探究二 例题讲解
问题 上述运算应用了什么运算律?
答:应用分配律、交换律和结合律.
问题 整式加减的实质是什么?
答:去括号、合并同类项.
[方法归纳]
(1)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算;
(2)整式加减实际上就是:去括号、合并同类项;
(3)运算结果,常将多项式的某个字母(如x)降幂(升幂)排列.
探究二 整式的加化简求值
例2. 计算:
(1)(4x -5xy+3y )-(3x +2y );
(2) [4×(-2) -5×(﹣2)×3+3×3 ]-[3×(-2) +2×3 ];
(3)[4×(﹣b) -5×(﹣b)×c+3×c ]-[3×(-b) +2×c ]
分析:将(2)与(1)进行比较,发现将(1)中的字母x,y分别用﹣2,3代入可得(2),于是(1)中的结果中的字母x,y分别用﹣2,3代入,即可得(2)的结果,类似地,可以求得(3)的计算结果.
探究二 整式的加化简求值
解:(1)(4x -5xy+3y )-(3x +2y )
=4x -5xy+3y -3x -2y
=x -5xy+y ;
(2)将等式①中的x用一2,y用3代入,则
[4×(-2) -5×(﹣2)×3+3×3 ]-[3×(-2) +2×3 ]
=(﹣2) -5×(﹣2)×3+3
=4+30+9
=43.
(去括号)
(合并同类项)
(代入化简后的式子)
探究二 整式的加减化简求值
(3)将等式①中的x用一b代人,则
[4×(﹣b) -5×(﹣b)×c+3×c ]-[3×(-b) +2×c ]
=(﹣b) -5×(﹣b)c+c
=b +5bc+c .
小结:
(1)多项式的重要性:
要将一个多项式经过计算得到的等式中的字母,用任意数或任意多项式代人,就可得到许多等式,这休现了多项式的重要性。
(2)多项式的化简求值
先把原多项式去括号、合并同类项,再把给定的条件代入化简后的式子进行计算.
等式中的字母可以用任意数会任意多项式代入
例3.做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
a
b
c
1.5a
2b
2c
探究三 整式加减的应用
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm2 )
解:小纸盒的表面积是( )cm2
2ab
+2bc
+2ca
大纸盒的表面积是( )cm2
6ab
+8bc
+ 6ca
整式加减解决实际问题的一般步骤:
⑴ 根据题意列代数式;
⑵ 去括号、合并同类项.;
⑶ 得出最后结果.
总结归纳
当堂达标
叁
当堂达标
1.化简2(x+ )- (3x-6)的结果是( )
A.3x+3 B.3x-3 C.x+3 D.x-3
2.多项式2x3-10x2+4x-1与多项式3x3-4x-5x2+3相加,合并后不含的项是( )
A.三次项 B.二次项 C.一次项 D.常数项
3.一个两位数,它的十位数字是a,个位数字是b,将这个两位数的个位数字和十位数字交换位置后得到一个新的两位数,求所得数与原数的和 (用含a,b的代数式表示).
C
C
叁
11(a+b)
4.先计算,2(-5x+x)+(3x-2x)-3(-x+7x), 再利用所得结果计算:
2[×-5×(﹣1)]+[3×(﹣1)×-2×(﹣1)]-3[(﹣1)3×-(﹣1)+7×(﹣1)].
解:2(-5x+x)+(3x-2x)-3(-x+7x)
=2-10x+2x+3x-2x-3+3x21x
=(2-3)-10)+3+3]x+[2+(-2)+(﹣21)]x
=--4x-21x
解:2[×-5×(﹣1)]+[3×(﹣1)×-2×(﹣1)]-3[(﹣1)3×-(﹣1)+7×(﹣1)
=--4×(﹣1)×-21×(﹣1)
=57
5.某校有A,B,C三个课外活动小组,A小组有学生(x+2y)名,B小组学生人数是A小组学生人数的3倍,C小组比A小组多3名学生,问A,B,C三个课外活动小组共有多少名学生
解:B小组学生人数为3(x+2y)名,C小组学生人数为[(x+2y)+3]名.
(x+2y)+3(x+2y)+(x+2y)+3=5(x+2y)+3
=(5x+10y+3)(名).
答:A,B,C三个课外活动小组共有(5x+10y+3)名学生.
课堂小结
肆
课堂小结
1.整式加减:
几个整式相加减,如果有括号就先去括号,然后再合并同类项.
2.化简求值时,一般先将整式进行化简,再把数值代入化简后的式子计算.
3.利用整式加减解决实际问题的一般步骤:
(1)根据题意列式;(2)去括号、合并同类项;(3)得出最后结果.
肆
课后作业
基础题:1.课后练习 第 1 题。
提高题:2.请学有余力的同学完成课后习题第4,5题
谢
谢
同课章节目录
