13.3.2 三角形的外角 课件(共18张PPT) 2025-2026学年数学人教版(2024)八年级上册
文档属性
| 名称 | 13.3.2 三角形的外角 课件(共18张PPT) 2025-2026学年数学人教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 05:58:07 | ||
图片预览



文档简介
(共18张PPT)
13.3.2 三角形的外角
第十三章 三角形
01
理解三角形外角的概念,能识别三角形的外角.
02
掌握三角形的外角的性质,并能运用这些性质解决简单的问题.
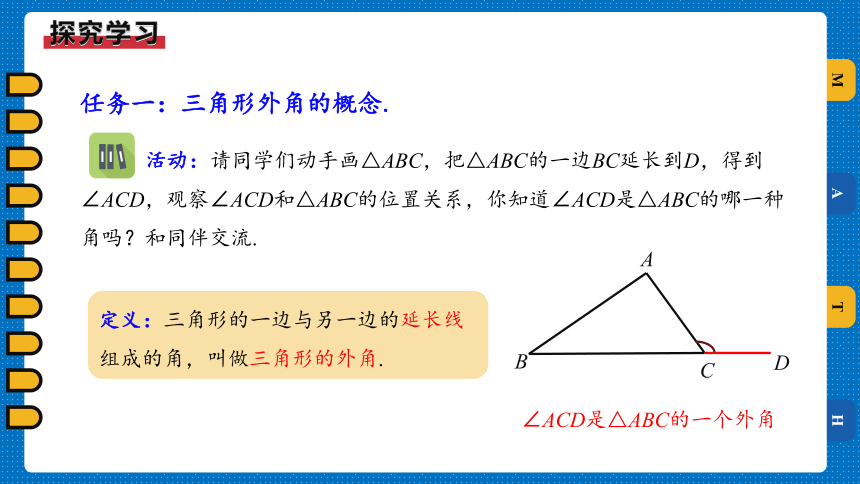
任务一:三角形外角的概念.
C
B
A
D
∠ACD是△ABC的一个外角
定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
活动:请同学们动手画△ABC,把△ABC的一边BC延长到D,得到∠ACD,观察∠ACD和△ABC的位置关系,你知道∠ACD是△ABC的哪一种角吗?和同伴交流.
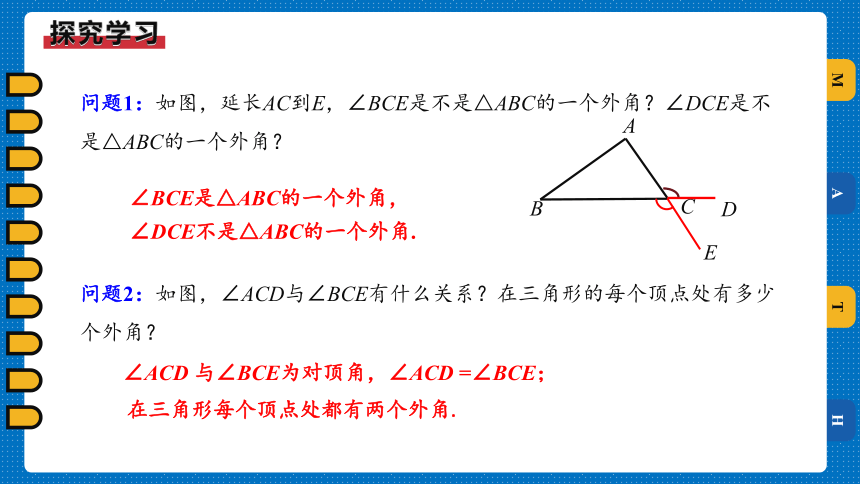
问题1:如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
∠DCE不是△ABC的一个外角.
C
B
A
D
E
问题2:如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
在三角形每个顶点处都有两个外角.
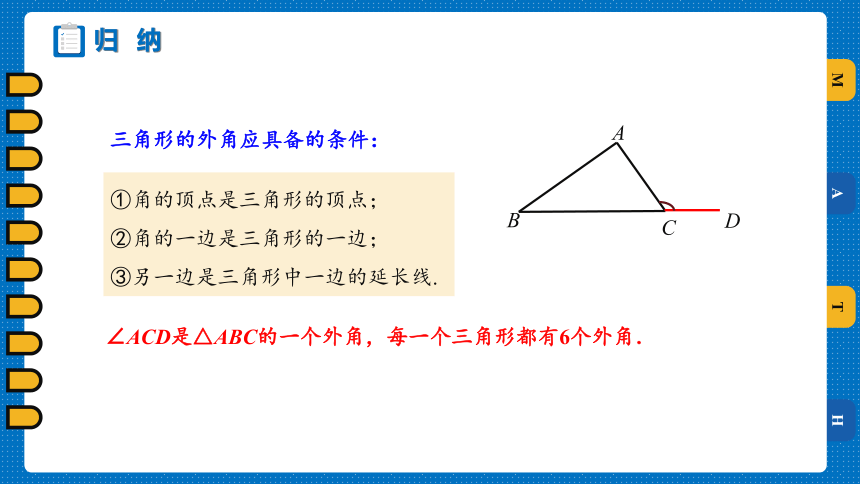
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
C
B
A
D
∠ACD是△ABC的一个外角,每一个三角形都有6个外角.
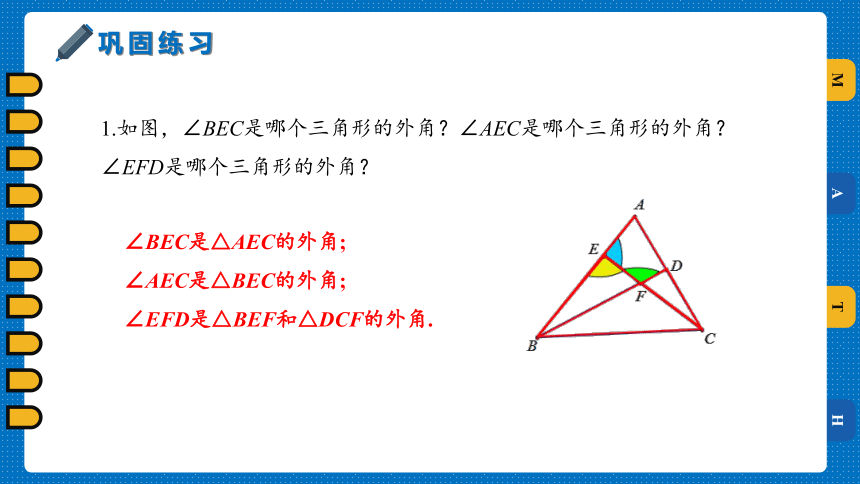
1.如图,∠BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
问题1:如图,△ABC的外角∠CBD与其相邻的内角∠ABC有什么关系?
A
B
C
D
任务二:三角形的外角的性质
活动:我们已经知道了三角形外角的概念,那么三角形的外角与三角形的内角有哪些关系呢?和同伴交流,回答以下问题.
BD为AB边延长线,所以与AB边共直线,
∴∠ABC+∠CBD=180°,
∴∠ABC与∠CBD互补.
A
B
C
D
问题2:在△ABC中,外角∠CBD和与它不相邻的内角,∠A和∠C在大小上有什么关系?
∠A+∠C+∠ABC=180°,
∠ABC+∠CBD=180°,
所以∠A+∠C=∠CBD.
归纳小结:1.三角形的外角与它相邻的内角互补.
2.三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
问题3:任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
如图,求证:∠ACD=∠A+∠B.(用作平行线的方法证明此结论.)
证明:过C作CE平行于AB,
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
1
2
E
2.说出下列图形中∠1和∠2的度数.
(
(
(
(
1
2
60°
75°
(1)
(
70°
1
2
(2)
(3)
(
(
(
(
(
2
1
50°
40°
60°
解:
在图(1)中,∠1=180°-60°-75°=45°,∠2=60°+75°=135°;
在图(2)中,∠1=90°-70°=20°,∠2=70°+90°=160°;
在图(3)中,∠2=50°+60°=110°,∠1=180°-∠2-40°=30°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
例4:如图,∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?试着算一算.
(
(
(
总结:如图,三角形的三个不同位置的外角和等于360°.
(
(
(
三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
3.判断下列观点是否正确.
(1)三角形的外角都是钝角. ( )
(2)三角形的外角大于任何一个内角. ( )
(3)三角形的外角等于它的两个内角的和. ( )
(4)三角形的外角和等于360°. ( )
分析:(1)三角形的外角是锐角、钝角或者直角.
(2)三角形的外角大于任何一个不相邻内角.
(3)三角形的外角等于它的不相邻两个内角的和.
×
×
×
√
经过本节课的学习,请回答以下问题。
1.说说三角形外角的定义和性质.
2.三角形的外角和是多少?
三角形的外角
定义
性质
三角形的外角和
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
三角形的外角和等于360°
1.如图,在△ABC中,CD是∠ACB的外角平分线,且CD∥AB,若∠ACB=100°,则∠B的度数为( )
A.35° B.40°C.45° D.50°
B
2.如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,则∠ADB的度数为 .
105°
3 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求∠B 和∠C的度数.
解:因为∠ADC是△ABD的外角,
所以∠ADC=∠B+∠BAD=80°,
又因为∠B=∠BAD,
所以∠B=40°
在△ABC中,∠B+∠BAC+∠C=180°,
所以∠C=180 -40 -70 =70°.
4. 如图,已知∠A=60°,∠B=20°,∠C=30°.求∠BDC的度数.
解:如图,延长BD交AC于点H,
∠BDC=∠DHC+∠C,
∠DHC=∠A+∠B.
∴∠BDC=∠A+∠B+∠C
=60°+20°+30°=110°.
H
13.3.2 三角形的外角
第十三章 三角形
01
理解三角形外角的概念,能识别三角形的外角.
02
掌握三角形的外角的性质,并能运用这些性质解决简单的问题.
任务一:三角形外角的概念.
C
B
A
D
∠ACD是△ABC的一个外角
定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
活动:请同学们动手画△ABC,把△ABC的一边BC延长到D,得到∠ACD,观察∠ACD和△ABC的位置关系,你知道∠ACD是△ABC的哪一种角吗?和同伴交流.
问题1:如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
∠DCE不是△ABC的一个外角.
C
B
A
D
E
问题2:如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
在三角形每个顶点处都有两个外角.
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
C
B
A
D
∠ACD是△ABC的一个外角,每一个三角形都有6个外角.
1.如图,∠BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
问题1:如图,△ABC的外角∠CBD与其相邻的内角∠ABC有什么关系?
A
B
C
D
任务二:三角形的外角的性质
活动:我们已经知道了三角形外角的概念,那么三角形的外角与三角形的内角有哪些关系呢?和同伴交流,回答以下问题.
BD为AB边延长线,所以与AB边共直线,
∴∠ABC+∠CBD=180°,
∴∠ABC与∠CBD互补.
A
B
C
D
问题2:在△ABC中,外角∠CBD和与它不相邻的内角,∠A和∠C在大小上有什么关系?
∠A+∠C+∠ABC=180°,
∠ABC+∠CBD=180°,
所以∠A+∠C=∠CBD.
归纳小结:1.三角形的外角与它相邻的内角互补.
2.三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
问题3:任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
如图,求证:∠ACD=∠A+∠B.(用作平行线的方法证明此结论.)
证明:过C作CE平行于AB,
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
1
2
E
2.说出下列图形中∠1和∠2的度数.
(
(
(
(
1
2
60°
75°
(1)
(
70°
1
2
(2)
(3)
(
(
(
(
(
2
1
50°
40°
60°
解:
在图(1)中,∠1=180°-60°-75°=45°,∠2=60°+75°=135°;
在图(2)中,∠1=90°-70°=20°,∠2=70°+90°=160°;
在图(3)中,∠2=50°+60°=110°,∠1=180°-∠2-40°=30°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
例4:如图,∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?试着算一算.
(
(
(
总结:如图,三角形的三个不同位置的外角和等于360°.
(
(
(
三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
3.判断下列观点是否正确.
(1)三角形的外角都是钝角. ( )
(2)三角形的外角大于任何一个内角. ( )
(3)三角形的外角等于它的两个内角的和. ( )
(4)三角形的外角和等于360°. ( )
分析:(1)三角形的外角是锐角、钝角或者直角.
(2)三角形的外角大于任何一个不相邻内角.
(3)三角形的外角等于它的不相邻两个内角的和.
×
×
×
√
经过本节课的学习,请回答以下问题。
1.说说三角形外角的定义和性质.
2.三角形的外角和是多少?
三角形的外角
定义
性质
三角形的外角和
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
三角形的外角和等于360°
1.如图,在△ABC中,CD是∠ACB的外角平分线,且CD∥AB,若∠ACB=100°,则∠B的度数为( )
A.35° B.40°C.45° D.50°
B
2.如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,则∠ADB的度数为 .
105°
3 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求∠B 和∠C的度数.
解:因为∠ADC是△ABD的外角,
所以∠ADC=∠B+∠BAD=80°,
又因为∠B=∠BAD,
所以∠B=40°
在△ABC中,∠B+∠BAC+∠C=180°,
所以∠C=180 -40 -70 =70°.
4. 如图,已知∠A=60°,∠B=20°,∠C=30°.求∠BDC的度数.
解:如图,延长BD交AC于点H,
∠BDC=∠DHC+∠C,
∠DHC=∠A+∠B.
∴∠BDC=∠A+∠B+∠C
=60°+20°+30°=110°.
H
同课章节目录
