3.2平面直角坐标系 课件(2课时、共40张PPT) 2025-2026学年数学北师大版八年级上册
文档属性
| 名称 | 3.2平面直角坐标系 课件(2课时、共40张PPT) 2025-2026学年数学北师大版八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 17:21:38 | ||
图片预览



文档简介
(共40张PPT)
3.2 平面直角坐标系 第1课时
第三章 位置与坐标
1.什么是数轴?
2.数轴的三要素是什么?
3.数轴上的点与实数之间有怎样的关系?
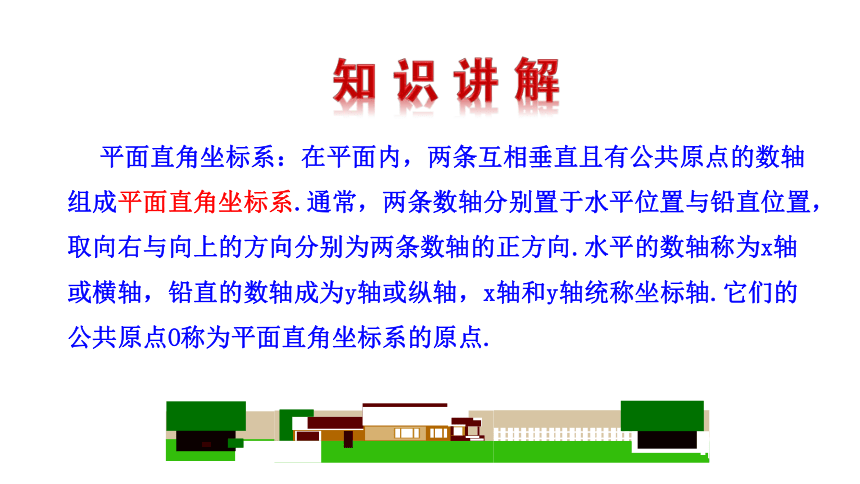
数轴上的点A表示数1.反过来,数1就是点A的位置.
同理可知,点B在数轴上表示的数是-3;点C在数轴上表示的数是2.5;点D在数轴上表示的数是0.
数轴上的点与实数之间存在着一一对应的关系.
O
1
2
3
4
5
-4
-3
-2
-1
A
C
B
D
1.理解平面直角坐标系的有关概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标找出点或由点求坐标.
3.了解平面内的点与有序实数对之间的一一对应关系.
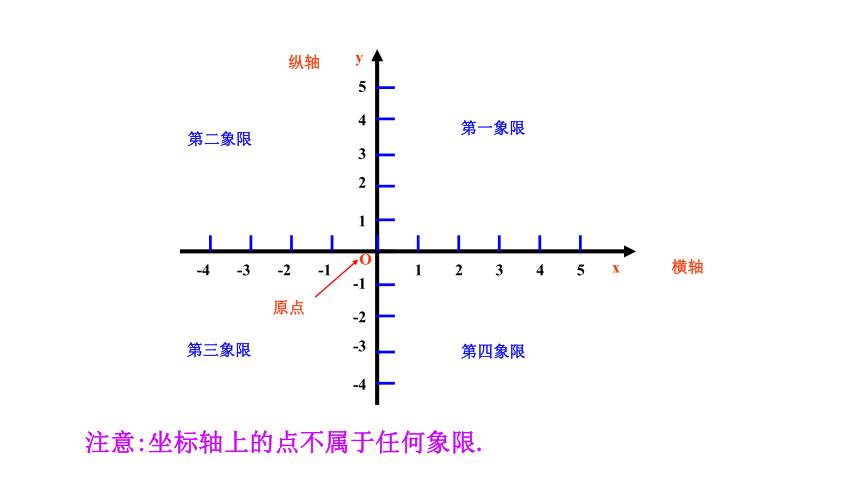
平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴称为x轴或横轴,铅直的数轴成为y轴或纵轴,x轴和y轴统称坐标轴.它们的公共原点O称为平面直角坐标系的原点.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限.
·
A
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
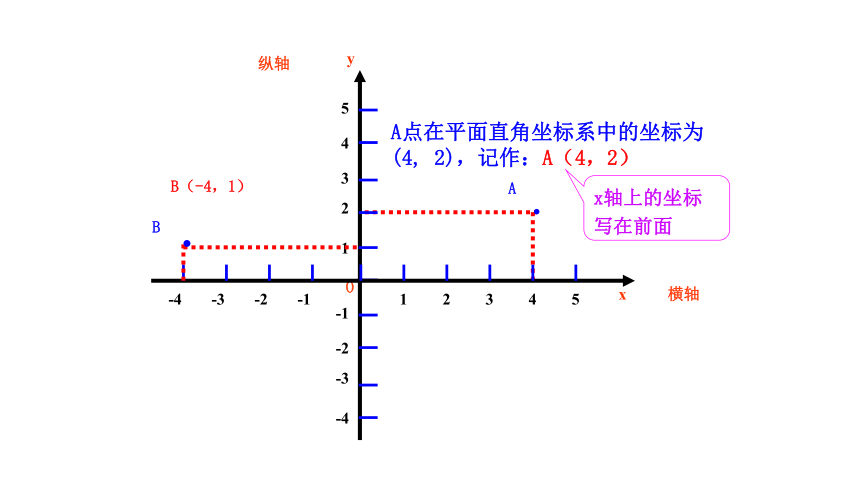
A点在平面直角坐标系中的坐标为
(4, 2),记作:A(4,2)
·
B
B(-4,1)
x轴上的坐标
写在前面
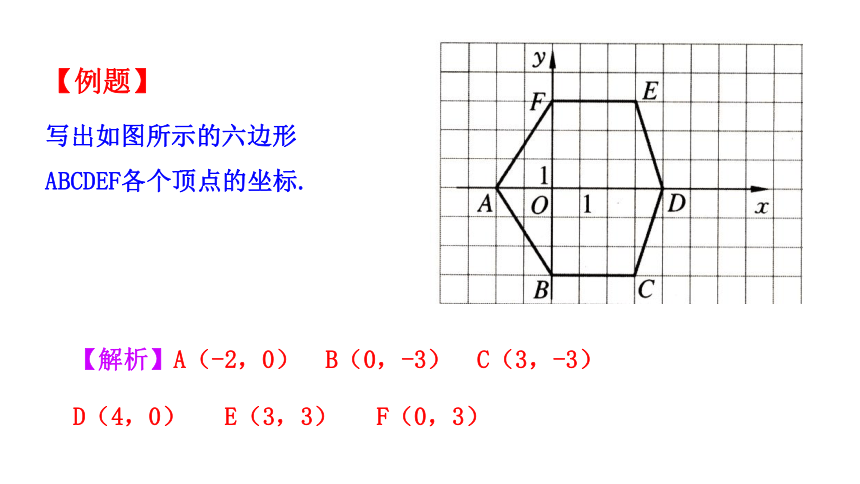
写出如图所示的六边形ABCDEF各个顶点的坐标.
【例题】
【解析】A(-2,0) B(0,-3) C(3,-3)
D(4,0) E(3,3) F(0,3)
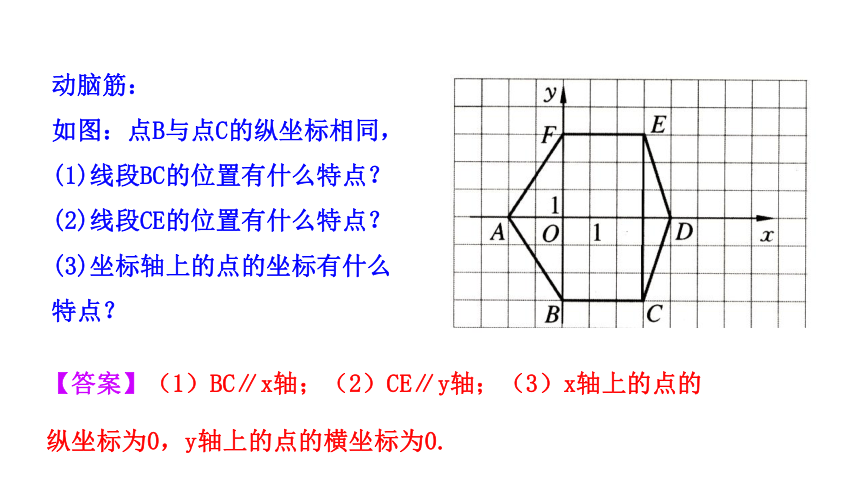
动脑筋:
如图:点B与点C的纵坐标相同,(1)线段BC的位置有什么特点?
(2)线段CE的位置有什么特点?
(3)坐标轴上的点的坐标有什么特点?
【答案】(1)BC∥x轴;(2)CE∥y轴;(3)x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
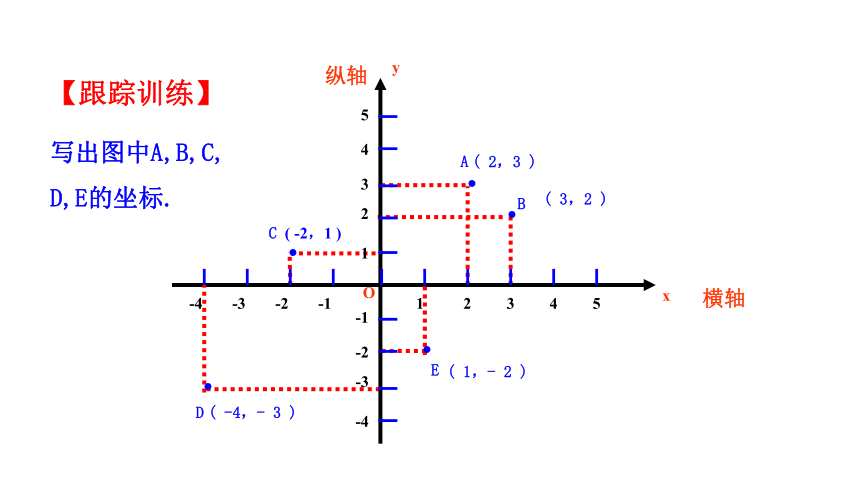
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
写出图中A,B,C,
D,E的坐标.
【跟踪训练】
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
·
P
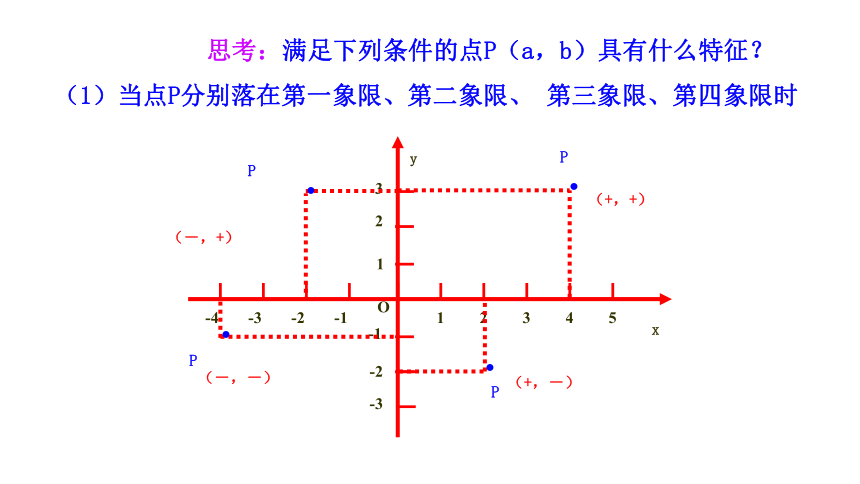
思考:满足下列条件的点P(a,b)具有什么特征?
(1)当点P分别落在第一象限、第二象限、 第三象限、第四象限时
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
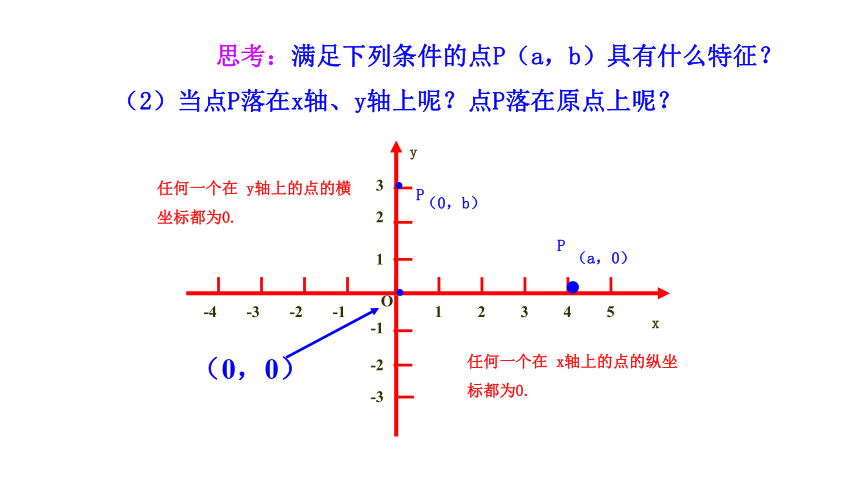
思考:满足下列条件的点P(a,b)具有什么特征?
(2)当点P落在x轴、y轴上呢?点P落在原点上呢?
x
y
·
(0,b)
P
(a,0)
·
P
(0,0)
任何一个在 x轴上的点的纵坐标都为0.
任何一个在 y轴上的点的横坐标都为0.
·
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
思考:满足下列条件的点P(a,b)具有什么特征?
(3)当点P落在第一、三象限的两条坐标轴夹角平分线上时.
x
y
(a,a)
P
·
·
P
a=b
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
思考:满足下列条件的点P(a,b)具有什么特征?
(4)当点P落在二、四象限的两条坐标轴夹角平分线上时
x
y
·
P
P
·
(a,-a)
a=-b
通过本课时的学习,需要我们掌握:
1.平面直角坐标系的概念,根据坐标找出点,由点求出坐标.
2.坐标平面分为四个象限:
各象限的符号:
(-,-)
(+,-)
(+,+)
(-,+)
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选A.第一象限的点,横、纵坐标都为正数.
A
2.在平面直角坐标系中,点A(2,﹣3)位于第 象限.
【解析】由象限内的点的坐标的符号规律可得,点A在第四象限.
答案:四
3.(1)若点A(a,b)在第三象限,则点Q(-a+1,b-5)位于第 _____象限.
(2)若点B(m+4,m-1)在x轴上,则m=_________.
(3)若点 C(x,y)满足x+y<0, xy>0 ,则点C位于第____象限.
【解析】(1)点A(a,b)在第三象限,则a<0,b<0.所以
-a+1>0, b-5<0,所以Q(-a+1,b-5)位于第四象限.
(2)点B(m+4,m-1)在x轴上,则m-1=0,m=1.
(3)由xy>0得x,y同号,因为x+y<0,则x<0, y<0,所以点 C(x,y)位于第三象限.
答案:(1)四 (2)1 (3)三
4.在平面直角坐标系中, 点A(0,8), 点B(6, 8).(1) 只用直尺(没有刻度)和圆规, 求作点P,使点P同时满足下列两个条件(要求保留作图痕迹, 不必写出作法): ①点P到A,B两点的距离相等;②点P到两坐标轴的距离相等. (2) 在(1)作出点后, 写出点P的坐标.
【解析】(1) 作图如右, 点P即为所求作的点;
(2) 设AB的中垂线交AB于E,交x轴于F,
由作图可得EF⊥AB,EF⊥x轴, 且OF =3,
因为OP是∠AOF的平分线,
所以点P的坐标为(3,3).
3.2 平面直角坐标系 第2课时
第三章 位置与坐标
3、如果给你一对有序实数对(可能是整数,可能是分数,也可能是无理数),那么你能在平面直角坐标系中描出它所对应的点吗?
2、图形中的一个点,它的坐标可能是整数、分数,可能是无理数吗?
【结论】有序实数对与平面直角坐标系中的点一一对应.
1、如果给你一对有序实数对,你能在平面直角坐标系中找出它所对应的点吗?
1.在给定的平面直角坐标系下,会根据坐标描出点的位置.
2.通过找点、连线、观察,确定图形的大致形状,并且能求出规则图形的面积,能进一步掌握平面直角坐标系的基本内容.
-1
o
y
x
-2
-6
2
6
2
6
在下图的平面直角坐标系中描出下列各点,并把各
点用线段依次连接起来.观察它是什么形状,并计算它的面积。
(0,4),(-4,-1),(-9,3).
【解析】形状为等腰直角三角形,直角边的长
为
【例1】
面积为
-1
o
y
x
-2
-6
2
6
2
6
在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来,观察它的形状并计算其面积.
(2,2)(5,6)
(-4,6)(-7,2)
【解析】如图,是平行四边形,它的面积为(7+2)×(6-2)=36
【跟踪训练】
在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来.
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6),
(2,6), (1,8), (0,6), (0,2), (2,0);
2.(1,3), (2,2), (4,2), (5,3);
3.(1,4), (2,4), (2,5), (1,5), (1,4);
4.(4,4), (5,4),(5,5), (4,5), (4,4);
5.(3,3).
【跟踪训练】
o
2
4
6
8
2
4
6
8
y
x
观察所得的图形,你觉得它像什么
【解析】答案不唯一,可以说像“猫脸”等
如图是某市旅游景点的示意图.
(1)“大成殿”在“中心广场”的
西、南各多少格?“碑林”在“中心广
场”的东、北各多少格?
【解析】 “大成殿”在“中心广场”的西、南各2格,“碑林”在“中心广场”的东3格,北1格.
【例2】
(2)如果中心广场处定为(0,0),一个小格的边长为1,你能表示“碑林”的位置吗?
x
y
【解析】如图,建立平面直角坐标系,“碑林”的位置为(3,1).
o
如图,长方形ABCD的长与宽分别为6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
D
A
B
C
【跟踪训练】
【解析】①以点B为坐标原点,分别以BC,BA所在直线为x轴、y轴,建立直角坐标系.坐标分别为A(0,4),B(0,0),C(6, 0),D(6,4).
A
B
C
D
x
y
6
4
O
【解析】②以长方形的中心为坐标原点,平行于BC,BA的直线为x轴、
y轴,建立直角坐标系.坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2)。(答案不唯一)
A
B
C
D
x
y
0
3
-3
2
-2
【追问】由上可知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
通过本课时的学习,需要我们掌握:
建立适当的直角坐标系,描述物体的位置,
关键是选好原点.
1. 在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
【解析】如图所示,当以OP为腰时,
分别以O,P为圆心,OP为半径画弧,与y轴
有三个交点Q2,Q4,Q3,当以OP为底时,
OP的垂直平分线与y轴有一个交点Q1.
B
1
2
3
4
1
O
3
2
–2
–1
–1
–2
–3
–4
–3
–4
y
A
B
C
x
2.对于边长为4的正三角形ABC,建立适当的直角坐标系,
写出各个顶点的坐标.
【解析】A(0,2 ),B(-2,0),C(2,0).
y
A
B
C
3.已知A(1,4), B(-4,0),C(2,0).
△ABC的面积是___.
4.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为 .
12
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
(-1,2)或(-1,-2)
O
3.2 平面直角坐标系 第1课时
第三章 位置与坐标
1.什么是数轴?
2.数轴的三要素是什么?
3.数轴上的点与实数之间有怎样的关系?
数轴上的点A表示数1.反过来,数1就是点A的位置.
同理可知,点B在数轴上表示的数是-3;点C在数轴上表示的数是2.5;点D在数轴上表示的数是0.
数轴上的点与实数之间存在着一一对应的关系.
O
1
2
3
4
5
-4
-3
-2
-1
A
C
B
D
1.理解平面直角坐标系的有关概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标找出点或由点求坐标.
3.了解平面内的点与有序实数对之间的一一对应关系.
平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴称为x轴或横轴,铅直的数轴成为y轴或纵轴,x轴和y轴统称坐标轴.它们的公共原点O称为平面直角坐标系的原点.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限.
·
A
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在平面直角坐标系中的坐标为
(4, 2),记作:A(4,2)
·
B
B(-4,1)
x轴上的坐标
写在前面
写出如图所示的六边形ABCDEF各个顶点的坐标.
【例题】
【解析】A(-2,0) B(0,-3) C(3,-3)
D(4,0) E(3,3) F(0,3)
动脑筋:
如图:点B与点C的纵坐标相同,(1)线段BC的位置有什么特点?
(2)线段CE的位置有什么特点?
(3)坐标轴上的点的坐标有什么特点?
【答案】(1)BC∥x轴;(2)CE∥y轴;(3)x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
写出图中A,B,C,
D,E的坐标.
【跟踪训练】
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
·
P
思考:满足下列条件的点P(a,b)具有什么特征?
(1)当点P分别落在第一象限、第二象限、 第三象限、第四象限时
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
思考:满足下列条件的点P(a,b)具有什么特征?
(2)当点P落在x轴、y轴上呢?点P落在原点上呢?
x
y
·
(0,b)
P
(a,0)
·
P
(0,0)
任何一个在 x轴上的点的纵坐标都为0.
任何一个在 y轴上的点的横坐标都为0.
·
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
思考:满足下列条件的点P(a,b)具有什么特征?
(3)当点P落在第一、三象限的两条坐标轴夹角平分线上时.
x
y
(a,a)
P
·
·
P
a=b
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
思考:满足下列条件的点P(a,b)具有什么特征?
(4)当点P落在二、四象限的两条坐标轴夹角平分线上时
x
y
·
P
P
·
(a,-a)
a=-b
通过本课时的学习,需要我们掌握:
1.平面直角坐标系的概念,根据坐标找出点,由点求出坐标.
2.坐标平面分为四个象限:
各象限的符号:
(-,-)
(+,-)
(+,+)
(-,+)
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选A.第一象限的点,横、纵坐标都为正数.
A
2.在平面直角坐标系中,点A(2,﹣3)位于第 象限.
【解析】由象限内的点的坐标的符号规律可得,点A在第四象限.
答案:四
3.(1)若点A(a,b)在第三象限,则点Q(-a+1,b-5)位于第 _____象限.
(2)若点B(m+4,m-1)在x轴上,则m=_________.
(3)若点 C(x,y)满足x+y<0, xy>0 ,则点C位于第____象限.
【解析】(1)点A(a,b)在第三象限,则a<0,b<0.所以
-a+1>0, b-5<0,所以Q(-a+1,b-5)位于第四象限.
(2)点B(m+4,m-1)在x轴上,则m-1=0,m=1.
(3)由xy>0得x,y同号,因为x+y<0,则x<0, y<0,所以点 C(x,y)位于第三象限.
答案:(1)四 (2)1 (3)三
4.在平面直角坐标系中, 点A(0,8), 点B(6, 8).(1) 只用直尺(没有刻度)和圆规, 求作点P,使点P同时满足下列两个条件(要求保留作图痕迹, 不必写出作法): ①点P到A,B两点的距离相等;②点P到两坐标轴的距离相等. (2) 在(1)作出点后, 写出点P的坐标.
【解析】(1) 作图如右, 点P即为所求作的点;
(2) 设AB的中垂线交AB于E,交x轴于F,
由作图可得EF⊥AB,EF⊥x轴, 且OF =3,
因为OP是∠AOF的平分线,
所以点P的坐标为(3,3).
3.2 平面直角坐标系 第2课时
第三章 位置与坐标
3、如果给你一对有序实数对(可能是整数,可能是分数,也可能是无理数),那么你能在平面直角坐标系中描出它所对应的点吗?
2、图形中的一个点,它的坐标可能是整数、分数,可能是无理数吗?
【结论】有序实数对与平面直角坐标系中的点一一对应.
1、如果给你一对有序实数对,你能在平面直角坐标系中找出它所对应的点吗?
1.在给定的平面直角坐标系下,会根据坐标描出点的位置.
2.通过找点、连线、观察,确定图形的大致形状,并且能求出规则图形的面积,能进一步掌握平面直角坐标系的基本内容.
-1
o
y
x
-2
-6
2
6
2
6
在下图的平面直角坐标系中描出下列各点,并把各
点用线段依次连接起来.观察它是什么形状,并计算它的面积。
(0,4),(-4,-1),(-9,3).
【解析】形状为等腰直角三角形,直角边的长
为
【例1】
面积为
-1
o
y
x
-2
-6
2
6
2
6
在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来,观察它的形状并计算其面积.
(2,2)(5,6)
(-4,6)(-7,2)
【解析】如图,是平行四边形,它的面积为(7+2)×(6-2)=36
【跟踪训练】
在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来.
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6),
(2,6), (1,8), (0,6), (0,2), (2,0);
2.(1,3), (2,2), (4,2), (5,3);
3.(1,4), (2,4), (2,5), (1,5), (1,4);
4.(4,4), (5,4),(5,5), (4,5), (4,4);
5.(3,3).
【跟踪训练】
o
2
4
6
8
2
4
6
8
y
x
观察所得的图形,你觉得它像什么
【解析】答案不唯一,可以说像“猫脸”等
如图是某市旅游景点的示意图.
(1)“大成殿”在“中心广场”的
西、南各多少格?“碑林”在“中心广
场”的东、北各多少格?
【解析】 “大成殿”在“中心广场”的西、南各2格,“碑林”在“中心广场”的东3格,北1格.
【例2】
(2)如果中心广场处定为(0,0),一个小格的边长为1,你能表示“碑林”的位置吗?
x
y
【解析】如图,建立平面直角坐标系,“碑林”的位置为(3,1).
o
如图,长方形ABCD的长与宽分别为6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
D
A
B
C
【跟踪训练】
【解析】①以点B为坐标原点,分别以BC,BA所在直线为x轴、y轴,建立直角坐标系.坐标分别为A(0,4),B(0,0),C(6, 0),D(6,4).
A
B
C
D
x
y
6
4
O
【解析】②以长方形的中心为坐标原点,平行于BC,BA的直线为x轴、
y轴,建立直角坐标系.坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2)。(答案不唯一)
A
B
C
D
x
y
0
3
-3
2
-2
【追问】由上可知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
通过本课时的学习,需要我们掌握:
建立适当的直角坐标系,描述物体的位置,
关键是选好原点.
1. 在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
【解析】如图所示,当以OP为腰时,
分别以O,P为圆心,OP为半径画弧,与y轴
有三个交点Q2,Q4,Q3,当以OP为底时,
OP的垂直平分线与y轴有一个交点Q1.
B
1
2
3
4
1
O
3
2
–2
–1
–1
–2
–3
–4
–3
–4
y
A
B
C
x
2.对于边长为4的正三角形ABC,建立适当的直角坐标系,
写出各个顶点的坐标.
【解析】A(0,2 ),B(-2,0),C(2,0).
y
A
B
C
3.已知A(1,4), B(-4,0),C(2,0).
△ABC的面积是___.
4.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为 .
12
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
(-1,2)或(-1,-2)
O
同课章节目录
