3.3 轴对称与坐标变化 课件(共21张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 3.3 轴对称与坐标变化 课件(共21张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 20:42:33 | ||
图片预览




文档简介
(共21张PPT)
3.3 轴对称与坐标变化
第三章 位置与坐标
1.探索图形坐标变化的过程.
2.掌握图形坐标变化与图形轴对称之间的关系.
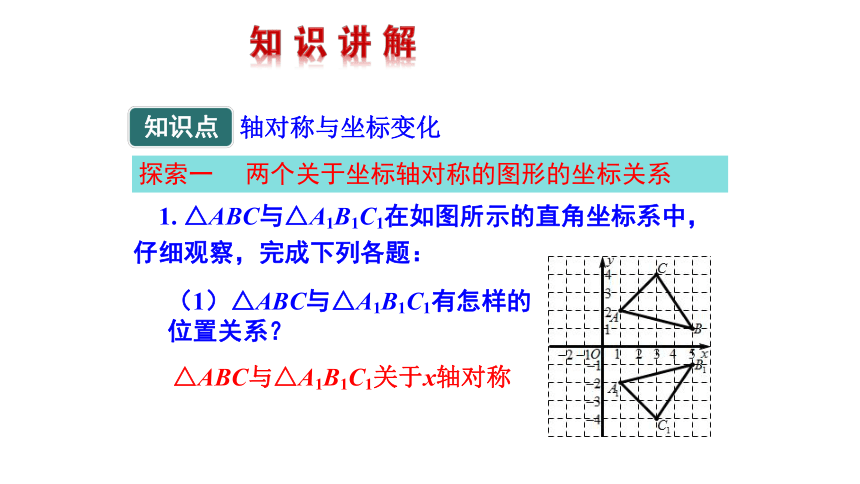
沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形;这条直线称为对称轴.
1.什么叫轴对称图形?
2.如何在平面直角坐标系中确定点P的位置?
称为点P的横坐标,
b称为点P的纵坐标.
复习引入
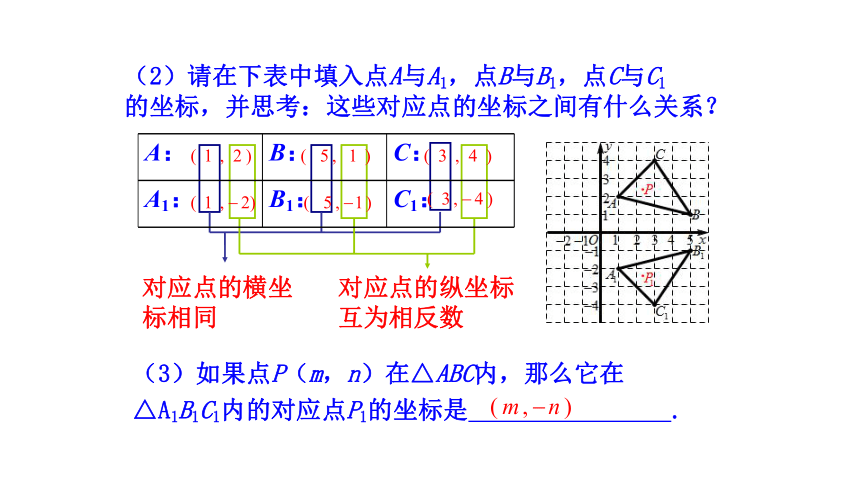
△ABC与△A1B1C1关于x轴对称
(1)△ABC与△A1B1C1有怎样的位置关系?
1. △ABC与△A1B1C1在如图所示的直角坐标系中,仔细观察,完成下列各题:
探索一 两个关于坐标轴对称的图形的坐标关系
轴对称与坐标变化
知识点
对应点的纵坐标互为相反数
对应点的横坐标相同
(2)请在下表中填入点A与A1,点B与B1,点C与C1
的坐标,并思考:这些对应点的坐标之间有什么关系?
C1:
B1:
A1:
C:
B:
A:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
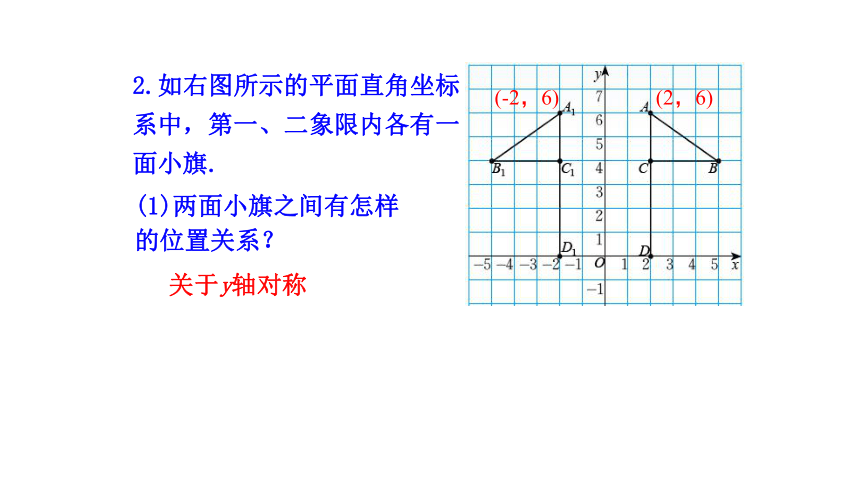
2.如右图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴对称
(2,6)
(-2,6)
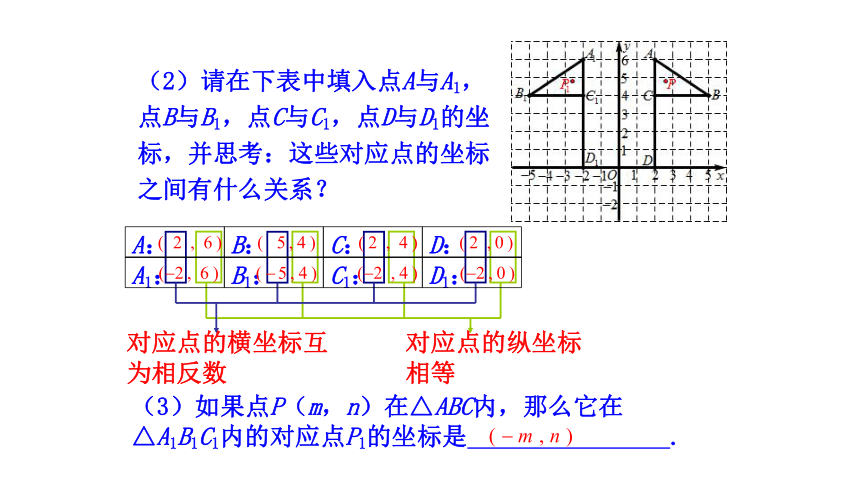
对应点的纵坐标相等
对应点的横坐标互为相反数
(2)请在下表中填入点A与A1,点B与B1,点C与C1,点D与D1的坐标,并思考:这些对应点的坐标之间有什么关系?
D1:
C1:
B1:
A1:
D:
C:
B:
A:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
3.通过以上学习,你知道关于x轴对称的两个点的坐标之间的关系吗?关于y轴对称的两个点的坐标之间的关系呢?
关于横轴对称的点,
横坐标相同;
关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
关于纵轴对称的点,
纵坐标相同.
2. 已知点A(a,1)与点A1(5,b)关于y轴对称,则a= ,b= .
1. 平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为 .
练一练
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
在平面直角坐标系中依次连接下列各点:(0,0), (5,4) ,(3,0),
(5,1) ,(5,-1), (3,0), (4,-2) ,(0,0),你得到了一个怎样的图案?
x
–1
y
探索二 坐标变化引起的图形变化
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘-1 ,则图形怎么变化?
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
两个图形关于y轴对称
将各坐标的纵坐标都乘-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
y
x
与原图形关于x轴对称
归纳总结
1.关于y轴对称的两个图形上点的坐标特征:
(x , y)
(-x , y)
2.关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
横坐标相同,纵坐标互为相反数.
横坐标互为相反数,纵坐标相同.
想一想
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 ________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 ______成轴对称.
x轴
y轴
讨论:点P(2,-3)到x轴、y轴和坐标原点的距离分别是多少?
O
1
1
-2
x
y
P(2,-3)
A
B
点M(-3,4)到x轴、y轴和坐标原点的距离分别是多少?
M(-3,4)
N
H
①点P( ,b)到x轴的距离是
②点P( ,b)到y轴的距离是
③点P( ,b)与坐标原点的距离是
x
y
o
P(a,b)
M
N
纵坐标的绝对值
横坐标的绝对值
归纳总结
1.点M(-5,12)到x轴的距离是____;到y轴的距离是____;到原点的距离是____.
2.已知点M(m,-5).①点M到x轴的距离是____;
②若点M到y轴的距离是4,那么 m 为____.
练一练
12
5
13
5
±4
轴对称与坐标变化
两个关于坐标轴对称的图形的坐标关系
坐标变化引起的图形变化
1.已知点A(1,﹣2)关于x轴的对称点是A′,则线段AA′=________.
2.已知点M(3,﹣2)与点N(a,b)关于y轴对称,则a=_____,b=______.
4
-3
-2
3.已知点A(a,5),B(﹣3,b),根据下列条件求出a,b的值.
(1)点A,B关于x轴对称;
(2)点A,B关于y轴对称.
解:(1)∵点A(a,5),B(﹣3,b),
点A,B关于x轴对称,∴a=﹣3,b=﹣5;
(2)∵点A,B关于y轴对称,
∴a=3,b=5.
4.已知线段AB的两个端点的坐标分别为A(-4,1),
B(-1,4),作出线段AB关于y轴对称的图形.
3
1
4
2
-1
O
1
2
3
4
-4
-3
-2
-1
x
y
·
·
A(-4,1)
B(-1,4)
A′(4,1)
B′(1,4)
·
·
【解析】点A(-4,1),B(-1,4),关于y轴对称点的坐标分别为A′(4,1),B′ (1,4).连接A′B′,就得到线段AB关于y轴对称的线段A′B′.
3.3 轴对称与坐标变化
第三章 位置与坐标
1.探索图形坐标变化的过程.
2.掌握图形坐标变化与图形轴对称之间的关系.
沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形;这条直线称为对称轴.
1.什么叫轴对称图形?
2.如何在平面直角坐标系中确定点P的位置?
称为点P的横坐标,
b称为点P的纵坐标.
复习引入
△ABC与△A1B1C1关于x轴对称
(1)△ABC与△A1B1C1有怎样的位置关系?
1. △ABC与△A1B1C1在如图所示的直角坐标系中,仔细观察,完成下列各题:
探索一 两个关于坐标轴对称的图形的坐标关系
轴对称与坐标变化
知识点
对应点的纵坐标互为相反数
对应点的横坐标相同
(2)请在下表中填入点A与A1,点B与B1,点C与C1
的坐标,并思考:这些对应点的坐标之间有什么关系?
C1:
B1:
A1:
C:
B:
A:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
2.如右图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴对称
(2,6)
(-2,6)
对应点的纵坐标相等
对应点的横坐标互为相反数
(2)请在下表中填入点A与A1,点B与B1,点C与C1,点D与D1的坐标,并思考:这些对应点的坐标之间有什么关系?
D1:
C1:
B1:
A1:
D:
C:
B:
A:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
3.通过以上学习,你知道关于x轴对称的两个点的坐标之间的关系吗?关于y轴对称的两个点的坐标之间的关系呢?
关于横轴对称的点,
横坐标相同;
关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
关于纵轴对称的点,
纵坐标相同.
2. 已知点A(a,1)与点A1(5,b)关于y轴对称,则a= ,b= .
1. 平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为 .
练一练
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
在平面直角坐标系中依次连接下列各点:(0,0), (5,4) ,(3,0),
(5,1) ,(5,-1), (3,0), (4,-2) ,(0,0),你得到了一个怎样的图案?
x
–1
y
探索二 坐标变化引起的图形变化
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘-1 ,则图形怎么变化?
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
两个图形关于y轴对称
将各坐标的纵坐标都乘-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
y
x
与原图形关于x轴对称
归纳总结
1.关于y轴对称的两个图形上点的坐标特征:
(x , y)
(-x , y)
2.关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
横坐标相同,纵坐标互为相反数.
横坐标互为相反数,纵坐标相同.
想一想
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 ________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 ______成轴对称.
x轴
y轴
讨论:点P(2,-3)到x轴、y轴和坐标原点的距离分别是多少?
O
1
1
-2
x
y
P(2,-3)
A
B
点M(-3,4)到x轴、y轴和坐标原点的距离分别是多少?
M(-3,4)
N
H
①点P( ,b)到x轴的距离是
②点P( ,b)到y轴的距离是
③点P( ,b)与坐标原点的距离是
x
y
o
P(a,b)
M
N
纵坐标的绝对值
横坐标的绝对值
归纳总结
1.点M(-5,12)到x轴的距离是____;到y轴的距离是____;到原点的距离是____.
2.已知点M(m,-5).①点M到x轴的距离是____;
②若点M到y轴的距离是4,那么 m 为____.
练一练
12
5
13
5
±4
轴对称与坐标变化
两个关于坐标轴对称的图形的坐标关系
坐标变化引起的图形变化
1.已知点A(1,﹣2)关于x轴的对称点是A′,则线段AA′=________.
2.已知点M(3,﹣2)与点N(a,b)关于y轴对称,则a=_____,b=______.
4
-3
-2
3.已知点A(a,5),B(﹣3,b),根据下列条件求出a,b的值.
(1)点A,B关于x轴对称;
(2)点A,B关于y轴对称.
解:(1)∵点A(a,5),B(﹣3,b),
点A,B关于x轴对称,∴a=﹣3,b=﹣5;
(2)∵点A,B关于y轴对称,
∴a=3,b=5.
4.已知线段AB的两个端点的坐标分别为A(-4,1),
B(-1,4),作出线段AB关于y轴对称的图形.
3
1
4
2
-1
O
1
2
3
4
-4
-3
-2
-1
x
y
·
·
A(-4,1)
B(-1,4)
A′(4,1)
B′(1,4)
·
·
【解析】点A(-4,1),B(-1,4),关于y轴对称点的坐标分别为A′(4,1),B′ (1,4).连接A′B′,就得到线段AB关于y轴对称的线段A′B′.
同课章节目录
