4.2 认识一次函数 课件(共29张PPT) 2025-2026学年数学北师大版八年级上册
文档属性
| 名称 | 4.2 认识一次函数 课件(共29张PPT) 2025-2026学年数学北师大版八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 17:22:47 | ||
图片预览






文档简介
(共29张PPT)
4.2 认识一次函数
第四章 一次函数
1.了解“均匀”变化.
2.掌握一次函数、正比例函数的概念.
3.能根据条件求出一次函数的关系式.
如果设青蛙的数量为x,y分别表示青蛙嘴的数量,眼睛的数量,腿的数量,扑通声,你能列出相应的函数解析式吗?
y表示青蛙嘴的数量:y=x
y表示青蛙眼睛的数量:y=2x
y表示青蛙腿的数量:y=4x
y表示扑通声的数量:y=x
情境引入
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子
“均匀”变化
知识点1
情景一:(1)将水龙头拧到适当位置,造成滴漏现象,在水龙头下方放一个量杯. 每隔1min,记录一下量杯中的水量,并将数据填入下表. 在坐标纸上描出(t,V)对应的点。你认为漏水量的变化具有什么规律 请你估计:这个水龙头一天的漏水量是多少
时间t/min 1 2 3 4 5 6 7 8 9 10 …
漏水量V/mL
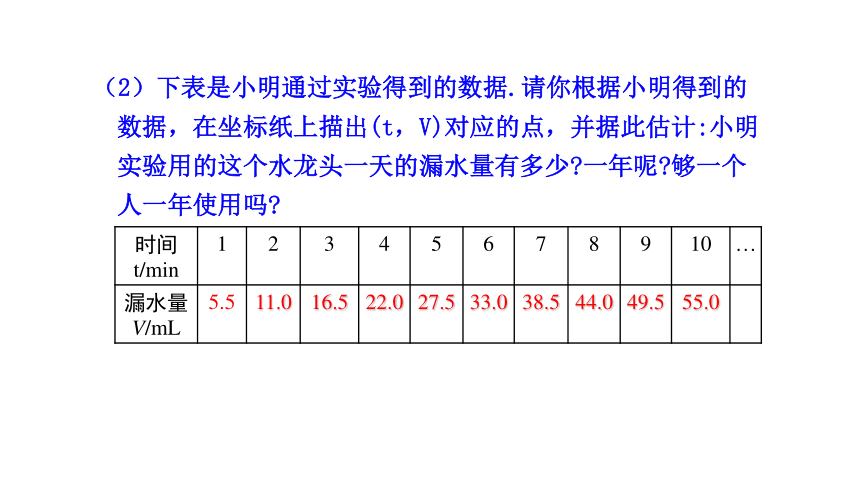
(2)下表是小明通过实验得到的数据.请你根据小明得到的数据,在坐标纸上描出(t,V)对应的点,并据此估计:小明实验用的这个水龙头一天的漏水量有多少 一年呢 够一个人一年使用吗
时间t/min 1 2 3 4 5 6 7 8 9 10 …
漏水量V/mL 5.5 11.0 16.5 22.0 27.5 33.0 38.5 44.0 49.5 55.0
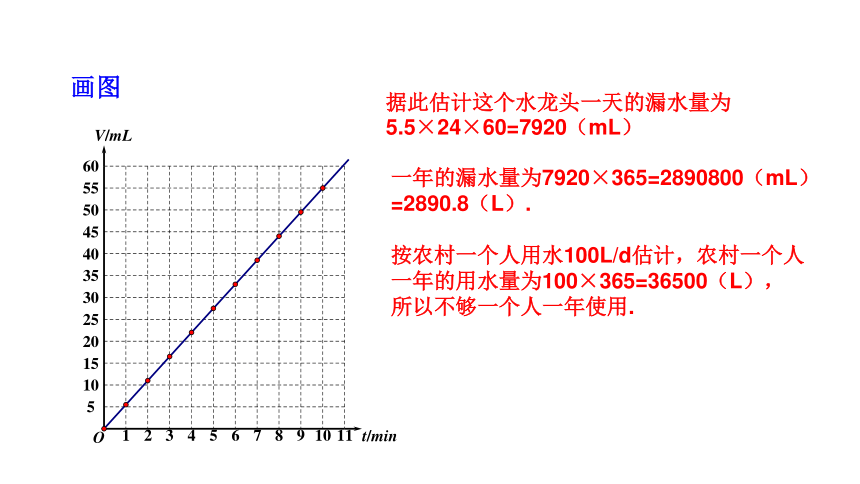
画图
据此估计这个水龙头一天的漏水量为5.5×24×60=7920(mL)
一年的漏水量为7920×365=2890800(mL)=2890.8(L).
按农村一个人用水100L/d估计,农村一个人一年的用水量为100×365=36500(L),
所以不够一个人一年使用.
(3)分析小明的实验数据,你能帮他写出漏水量 V与时间t之间的关系式吗
(4)你的实验结果与小明的实验结果有何异同
V=5.5t
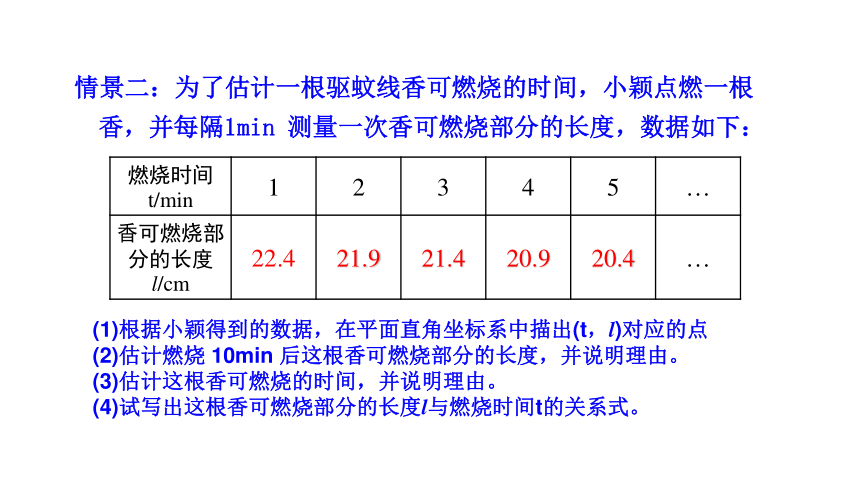
情景二:为了估计一根驱蚊线香可燃烧的时间,小颖点燃一根香,并每隔1min 测量一次香可燃烧部分的长度,数据如下:
燃烧时间t/min 1 2 3 4 5 …
香可燃烧部分的长度l/cm 22.4 21.9 21.4 20.9 20.4 …
(1)根据小颖得到的数据,在平面直角坐标系中描出(t,l)对应的点
(2)估计燃烧 10min 后这根香可燃烧部分的长度,并说明理由。
(3)估计这根香可燃烧的时间,并说明理由。
(4)试写出这根香可燃烧部分的长度l与燃烧时间t的关系式。
【解析】(1)描点画图
(2)估计10min 后这根香可燃烧部分的长度为18.4cm,理由:根据表格可知,每分钟香的长度减少0.5cm,所以10min后的长度为20.4-4×0.5=18.4(cm).
(3)这根香可燃烧的时间为45.8min.
(4)这根香可燃烧部分的长度l与燃烧时间t的关系式为
l=22.9-0.5t.
(1)随着所挂物体质量x的增加,弹簧长度y的增长是“均匀”的吗
(2)写出y与x之间的关系式,并说明理由.
y=0.5x+3
情景一:在弹性限度内,某弹簧的长度y(单位:cm)与所挂物体的质量x(单位:kg)的关系如下表所示:
x/kg 0 1 2 3 4 5
y/cm
3.0
3.5
4.0
4.5
5.0
5.5
一次函数与正比例函数
知识点2
是
情景二:某辆汽车油箱中原有油40 L,汽车每行驶50 km耗油4 L.
(1) 完成下表:
行使路程x/km 0 50 100 150 200 300
耗油量y/L
0
4
8
12
16
20
(2)写出耗油量y与汽车行驶路程x之间的关系式.
(3)写出油箱剩余油量z(单位:L)与汽车行驶路程x之间的关系式.
特别地,当b=0时,称y是x的正比例函数.
大家讨论一下,这三个函数关系式有什么特点
如果两个变量 x,y之间的对应关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,那么称 y是x的一次函数.(x为自变量,y为因变量.)
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4; (2)y=5x2-6; (3)y=2πx;
(6)y=8x2+x(1-8x)
解:(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
练一练
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数
项为零.
典例精析
例1:写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
解:由路程=速度×时间,得y=60x ,y是x的一次函数,也是正比例函数.
解:由圆的面积公式,得y=πx2,
y不是x的正比例函数,也不是一次函数.
(2)圆的面积y (cm2 )与它的半径x (cm)之间的关系.
解:这个水池每小时增加5m3水,x h增加5x m3水,
因而 y=15+5x,
y是x的一次函数,但不是x的正比例函数.
(3)某水池有水15m3,现打开进水管进水,进水速度为5m3/h,x h后这个水池有水y m3.
例2:在一次测试中,某汽车紧急刹车后,每过1s其速度减少35km/h.
(1)假设该汽车以120km/h的速度行驶,试写出该汽车刹车后的速度y(单位:km/h)与刹车后所经过的时间t(单位:s)之间的关系式y=kx+b,并说明k和b的实际意义;
解:刹车开始时汽车的速度为120km/h,每经过1s汽车的速度减少35km/h,于是经过ts汽车的速度减少了35tkm/h,所以y与t的关系式是y=-35t+120.其中,k=-35表示每秒汽车速度的变化量,b=120表示刹车开始时汽车的速度.
(2)求出(1)中汽车从刹车到停止所需的时间.
【方法总结】当b=0时,一次函数为正比例函数.
变式训练
(1)若 是正比例函数,则m= ;
(2)若 是正比例函数,则m= ;
-2
-1
m-2≠0,
|m|-1=1,
∴ m=-2.
m-1≠0,
m2-1=0,
∴ m=-1.
例3 为了鼓励市民节约用水,某市采用分档计费的方式计算水费.下表是家庭人口不超过4人时户用水量及分档计费标准.
能力提升
(1)当220(2)某户一年用水量是250m3,求该户一年的水费;
(3)某户去年一年的水费是1000.5元,求该户去年一年的用水量.
计费档 户年用水量x/m3 单价/(元/m3)
第一档 0<x≤220 3.45
第二档 220<x≤300 4.83
第三档 x>300 5.83
解:(1)当220<x≤300时,用水量属于第二档.于是
y=3.45×220+4.83×(x-220),
y=4.83x-303.6
(2)当x=250时,y=4.83×250-303.6=903.9(元)
(3)因为3.45×20=759,4.83×300-303.6=1145.4,
759<1000.5<1145.4,
所以该户年用水量为x m3,则1000.5=4.83-303.6
解这个方程,得 x=270.
因此,该户去年一年的用水量为270m3.
一次函数
一次函数的概念
正比例函数的概念
函数关系式的确定及分段函数
2. 甲乙两地相距264千米,一辆汽车从甲地开往乙地,每小时行驶24千米,t小时后,停在途中加水,则所剩路程s与行驶时间t之间的关系式 ______________,s是t的________函数.
一次
C
1.函数y=2x-3,当x=1时, y的值是( )
A、1 B、0 C、-1 D、-5
3.已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.
2x
1
2
y
0< <10
-6< <10
0-124.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为一次函数;
(2)此函数为正比例函数.
解:(1)由题意得: k = 2-m≠0, m≠2,所以m≠2时,
此函数为一次函数.
(2)由题意得: k = 2-m≠0, 解得:m≠2,
又因为b = 2m-3= 0, 解得:m=
所以当 m= 时,函数为正比例函数y= x.
5.某地区电话的月租费为25元,在此基础上,可免费打50次市话(每次3分钟),超过50次后,每次0.2元.
(1)写出每月电话费y(元)与通话次数x(x>50)的函数关系式;
解: 根据题意得:
y=25+(x-50)×0.2 ,
即 y=0.2x+15;
(2)求出月通话150次的电话费;
(3)如果某月通话费为53.6元,求该月通话的次数.
(2) 当x=150时, y=0.2×150+15=45;
(3) 因为53.6 > 25,可知通话次数大于50次,即当y=53.6时, 53.6=0.2x+15,解得:x=193.
解:
解:由x=2时y=-1,得 -1=2k+b;
由x=5时y=8,得 8=5k+b.
解二元一次方程组
得 k=3, b=-7.
∴ k的值为3, b的值为-7。
6.已知一次函数y=kx+b,当自变量x=2时,
函数值y=-1;当x=5时,y=8。求k,b的值。
4.2 认识一次函数
第四章 一次函数
1.了解“均匀”变化.
2.掌握一次函数、正比例函数的概念.
3.能根据条件求出一次函数的关系式.
如果设青蛙的数量为x,y分别表示青蛙嘴的数量,眼睛的数量,腿的数量,扑通声,你能列出相应的函数解析式吗?
y表示青蛙嘴的数量:y=x
y表示青蛙眼睛的数量:y=2x
y表示青蛙腿的数量:y=4x
y表示扑通声的数量:y=x
情境引入
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子
“均匀”变化
知识点1
情景一:(1)将水龙头拧到适当位置,造成滴漏现象,在水龙头下方放一个量杯. 每隔1min,记录一下量杯中的水量,并将数据填入下表. 在坐标纸上描出(t,V)对应的点。你认为漏水量的变化具有什么规律 请你估计:这个水龙头一天的漏水量是多少
时间t/min 1 2 3 4 5 6 7 8 9 10 …
漏水量V/mL
(2)下表是小明通过实验得到的数据.请你根据小明得到的数据,在坐标纸上描出(t,V)对应的点,并据此估计:小明实验用的这个水龙头一天的漏水量有多少 一年呢 够一个人一年使用吗
时间t/min 1 2 3 4 5 6 7 8 9 10 …
漏水量V/mL 5.5 11.0 16.5 22.0 27.5 33.0 38.5 44.0 49.5 55.0
画图
据此估计这个水龙头一天的漏水量为5.5×24×60=7920(mL)
一年的漏水量为7920×365=2890800(mL)=2890.8(L).
按农村一个人用水100L/d估计,农村一个人一年的用水量为100×365=36500(L),
所以不够一个人一年使用.
(3)分析小明的实验数据,你能帮他写出漏水量 V与时间t之间的关系式吗
(4)你的实验结果与小明的实验结果有何异同
V=5.5t
情景二:为了估计一根驱蚊线香可燃烧的时间,小颖点燃一根香,并每隔1min 测量一次香可燃烧部分的长度,数据如下:
燃烧时间t/min 1 2 3 4 5 …
香可燃烧部分的长度l/cm 22.4 21.9 21.4 20.9 20.4 …
(1)根据小颖得到的数据,在平面直角坐标系中描出(t,l)对应的点
(2)估计燃烧 10min 后这根香可燃烧部分的长度,并说明理由。
(3)估计这根香可燃烧的时间,并说明理由。
(4)试写出这根香可燃烧部分的长度l与燃烧时间t的关系式。
【解析】(1)描点画图
(2)估计10min 后这根香可燃烧部分的长度为18.4cm,理由:根据表格可知,每分钟香的长度减少0.5cm,所以10min后的长度为20.4-4×0.5=18.4(cm).
(3)这根香可燃烧的时间为45.8min.
(4)这根香可燃烧部分的长度l与燃烧时间t的关系式为
l=22.9-0.5t.
(1)随着所挂物体质量x的增加,弹簧长度y的增长是“均匀”的吗
(2)写出y与x之间的关系式,并说明理由.
y=0.5x+3
情景一:在弹性限度内,某弹簧的长度y(单位:cm)与所挂物体的质量x(单位:kg)的关系如下表所示:
x/kg 0 1 2 3 4 5
y/cm
3.0
3.5
4.0
4.5
5.0
5.5
一次函数与正比例函数
知识点2
是
情景二:某辆汽车油箱中原有油40 L,汽车每行驶50 km耗油4 L.
(1) 完成下表:
行使路程x/km 0 50 100 150 200 300
耗油量y/L
0
4
8
12
16
20
(2)写出耗油量y与汽车行驶路程x之间的关系式.
(3)写出油箱剩余油量z(单位:L)与汽车行驶路程x之间的关系式.
特别地,当b=0时,称y是x的正比例函数.
大家讨论一下,这三个函数关系式有什么特点
如果两个变量 x,y之间的对应关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,那么称 y是x的一次函数.(x为自变量,y为因变量.)
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4; (2)y=5x2-6; (3)y=2πx;
(6)y=8x2+x(1-8x)
解:(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
练一练
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数
项为零.
典例精析
例1:写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
解:由路程=速度×时间,得y=60x ,y是x的一次函数,也是正比例函数.
解:由圆的面积公式,得y=πx2,
y不是x的正比例函数,也不是一次函数.
(2)圆的面积y (cm2 )与它的半径x (cm)之间的关系.
解:这个水池每小时增加5m3水,x h增加5x m3水,
因而 y=15+5x,
y是x的一次函数,但不是x的正比例函数.
(3)某水池有水15m3,现打开进水管进水,进水速度为5m3/h,x h后这个水池有水y m3.
例2:在一次测试中,某汽车紧急刹车后,每过1s其速度减少35km/h.
(1)假设该汽车以120km/h的速度行驶,试写出该汽车刹车后的速度y(单位:km/h)与刹车后所经过的时间t(单位:s)之间的关系式y=kx+b,并说明k和b的实际意义;
解:刹车开始时汽车的速度为120km/h,每经过1s汽车的速度减少35km/h,于是经过ts汽车的速度减少了35tkm/h,所以y与t的关系式是y=-35t+120.其中,k=-35表示每秒汽车速度的变化量,b=120表示刹车开始时汽车的速度.
(2)求出(1)中汽车从刹车到停止所需的时间.
【方法总结】当b=0时,一次函数为正比例函数.
变式训练
(1)若 是正比例函数,则m= ;
(2)若 是正比例函数,则m= ;
-2
-1
m-2≠0,
|m|-1=1,
∴ m=-2.
m-1≠0,
m2-1=0,
∴ m=-1.
例3 为了鼓励市民节约用水,某市采用分档计费的方式计算水费.下表是家庭人口不超过4人时户用水量及分档计费标准.
能力提升
(1)当220
(3)某户去年一年的水费是1000.5元,求该户去年一年的用水量.
计费档 户年用水量x/m3 单价/(元/m3)
第一档 0<x≤220 3.45
第二档 220<x≤300 4.83
第三档 x>300 5.83
解:(1)当220<x≤300时,用水量属于第二档.于是
y=3.45×220+4.83×(x-220),
y=4.83x-303.6
(2)当x=250时,y=4.83×250-303.6=903.9(元)
(3)因为3.45×20=759,4.83×300-303.6=1145.4,
759<1000.5<1145.4,
所以该户年用水量为x m3,则1000.5=4.83-303.6
解这个方程,得 x=270.
因此,该户去年一年的用水量为270m3.
一次函数
一次函数的概念
正比例函数的概念
函数关系式的确定及分段函数
2. 甲乙两地相距264千米,一辆汽车从甲地开往乙地,每小时行驶24千米,t小时后,停在途中加水,则所剩路程s与行驶时间t之间的关系式 ______________,s是t的________函数.
一次
C
1.函数y=2x-3,当x=1时, y的值是( )
A、1 B、0 C、-1 D、-5
3.已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.
2x
1
2
y
0< <10
-6< <10
0
(1)此函数为一次函数;
(2)此函数为正比例函数.
解:(1)由题意得: k = 2-m≠0, m≠2,所以m≠2时,
此函数为一次函数.
(2)由题意得: k = 2-m≠0, 解得:m≠2,
又因为b = 2m-3= 0, 解得:m=
所以当 m= 时,函数为正比例函数y= x.
5.某地区电话的月租费为25元,在此基础上,可免费打50次市话(每次3分钟),超过50次后,每次0.2元.
(1)写出每月电话费y(元)与通话次数x(x>50)的函数关系式;
解: 根据题意得:
y=25+(x-50)×0.2 ,
即 y=0.2x+15;
(2)求出月通话150次的电话费;
(3)如果某月通话费为53.6元,求该月通话的次数.
(2) 当x=150时, y=0.2×150+15=45;
(3) 因为53.6 > 25,可知通话次数大于50次,即当y=53.6时, 53.6=0.2x+15,解得:x=193.
解:
解:由x=2时y=-1,得 -1=2k+b;
由x=5时y=8,得 8=5k+b.
解二元一次方程组
得 k=3, b=-7.
∴ k的值为3, b的值为-7。
6.已知一次函数y=kx+b,当自变量x=2时,
函数值y=-1;当x=5时,y=8。求k,b的值。
同课章节目录
