4.4一次函数的应用 课件(第1---2课时,42张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4.4一次函数的应用 课件(第1---2课时,42张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 20:53:59 | ||
图片预览










文档简介
(共42张PPT)
第四章 一次函数
4.4一次函数的应用
第1课时
超出起步价,怎么算?
超出免托运,怎么算?
1.了解两个条件可以确定一个一次函数,一个条件可
以确定一个正比例函数.
3.能够根据实际问题抽象出数学模型并利用一次函数
解决实际问题.
2.能根据所给信息(图象、表格等)确定一次函数的
表达式.
1.已知一个正比例函数,它的图象经过点(-1,2),则该函数表达式是_____.
-2
O
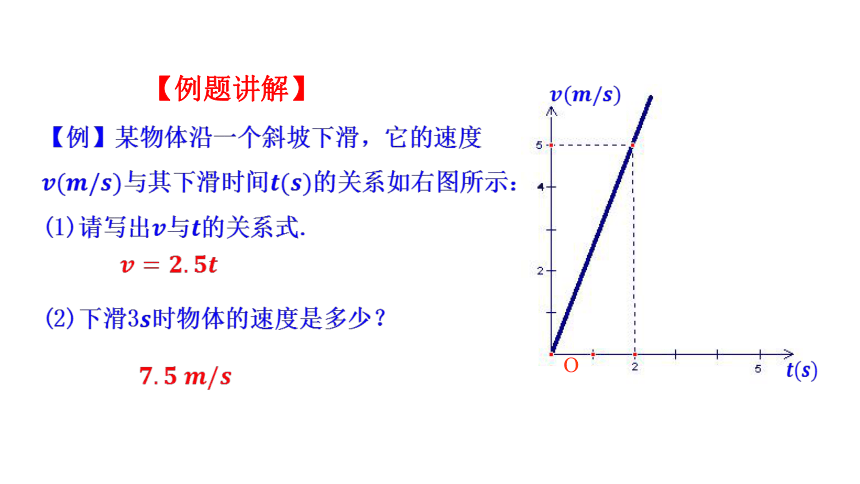
【例题讲解】
2.有同学画了如图一条直线的图象,
你知道该函数的表达式吗?
y
x
0
-3
2
6
8
-3
【跟踪训练】
【解析】
即当所挂物体的质量为4 kg时弹簧的长度为16.5cm。
A
1.已知四条直线y=kx-3,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或-2 B.2或-1
C.3 D.4
B
A.-1 B.1 C.5 D.-5
B
1
5.根据如图所示的条件,写出直线的表达式 ___________.
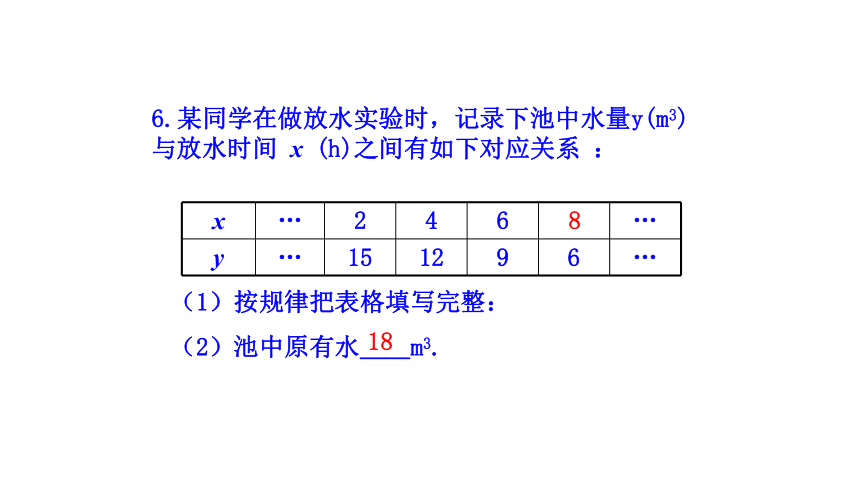
6.某同学在做放水实验时,记录下池中水量y(m3)与放水时间 x (h)之间有如下对应关系 :
x … 2 4 6 …
y … 15 12 9 6 …
(1)按规律把表格填写完整:
(2)池中原有水__m3.
8
18
7.已知一次函数y=kx-4,当x=2时,y=-3.
(1)求一次函数的关系式.
(2)将该函数的图象向上平行移动6个单位,求平行移动后的图象与x轴交点的坐标.
解决一次函数的表达式问题,一般采用待定系数法,这是初中数学的一种重要的方法 .
【规律方法】
本节课我们主要学习了根据已知条件,如何求函数的表达式:
1.设函数表达式.
3.解方程,求k,b.
第四章 一次函数
4.4一次函数的应用
第2课时
观察与思考
20
0
40
60
80
100
单位:cm
观察下图,你能发现它们三条函数直线之间的差别吗?
1.掌握两个一次函数图象的应用.(重点)
2.能利用函数图象解决数学问题.(难点)
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
引例:l1 反映了某公司产品的销售收入与销售量的关系,根据图意填空:
l1
当销售量为2吨时,销售收入= 元,
2000
销售收入
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了公司产品的销售收入与销售量的关系.
销售收入
l1对应的函数表达式是 ,
y=1000x
l1
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2 反映了公司产品的销售成本与销售量的关系
销售成本
l2对应的函数表达式是 .
y=500x+2000
l2
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
当销售成本为4500元时,销售量= 吨;
5
销售成本
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(1)当销售量为6吨时,销售收入= 元,
销售成本= 元, 利润= 元.
6000
5000
(2)当销售量为 时,销售收入等于销售成本.
4吨
销售收入
销售成本
1000
销售收入和销售成本都是4000元.
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(3)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本).
大于4吨
小于4吨
销售收入
销售成本
5
6
1
2
3
P
你还有什么发现?
7
8
【例题1】
假设甲、乙两人保持现有的速度,根据图象回答下列问题
(1)哪条线表示甲到观景台1的路程与追赶时间之间的关系
(2)甲和乙哪个人的速度快
(3)30min内甲能否追上乙
(4)到达观景台3后道路分岔,甲能否在到达观景台3前追上乙
(5)设l1与l2对应的两个一次函数分别为s=k1t+b1与s=k2t+b2,k1,
k2的实际意义各是什么 甲、乙两人的速度各是多少
1.A城有肥料200 t,B城有肥料300 t,现要把这些肥料全部运往C,D两乡.从A城往C,D两乡运肥料费用分别为每吨20元和25元;从B城往C,D两乡运肥料费用分别为每吨15元和24元.现C乡需要肥料240 t,D乡需要肥料260 t.怎样调运总运费最少?
分析:可以发现:A──C,A──D,B──C,B──D运肥料共涉及4个变量.它们都是影响总运费的变量.然而它们之间又有一定的必然联系,只要确定其中一个量,其余三个量也就随之确定.
【跟踪训练】
设A──C,x t,则:
由于A城有肥料200 t:A─D,(200-x) t.
由于C乡需要240 t:B─C,(240-x) t.
由于D乡需要260 t:B─D,(260-200+x) t.
那么,各段运输费用为:
A──C 20x
A──D 25(200-x)
B──C 15(240-x)
B──D 24(60+x)
【解析】
设总运费为y,y与x的关系为:
y=20x+25(200-x)+15(240-x)+24(60+x).
即:y=4x+10040 (0≤x≤200)
由关系式或图象都可看出,当x=0时,y值最小为10040.
因此,从A城运往C乡0t,运往D乡200 t;
从B城运往C乡240 t,运往D乡60t .
此时总运费最少,为10040元.
通过本课时的学习,需要我们掌握:
1.通过函数图象获取信息,发展形象思维.
2.利用函数图象解决简单的实际问题,发展数学的应用能力.
1. 如图,过点Q(0,3.5)的一次函数的图象与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是( )
A.3x-2y+3.5=0 B.3x-2y-3.5=0
C.3x-2y+7=0 D.3x+2y-7=0
【解析】设一次函数的关系式为y=kx+b,
又因为过Q(0,3.5),P(1,2)两点,
代入得y=-1.5x+3.5,整理得3x+2y-7=0.
D
2.甲、乙两人准备在一段长为1200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s,起跑前乙在起点,甲在乙前面100 m处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙
两人之间的距离y(m)与时间t(s)的函数图象是( )
【解析】设乙追上甲用x s,则6x-4x=100,x=50,乙跑完
全程用时1200÷6=200(s).
C
3. 一次函数y= x+4分别交x轴、y轴于A,B两点,在x轴上取
一点C,使△ABC为等腰三角形,则这样的点C有几个
【解析】在△ABC中,使△ABC为等腰三角形有AB=AC=
时,C点的坐标为(-4- ,0);( -4 ,0).当
AB=BC时,C点的坐标有(4,0);当AC=BC时,C点的坐标
有(0,0),故有4个.
4.小刚上午7:30从家里出发步行上学,途经少年宫时走了1200步,用时10 min,到达学校的时间是7:55.为了估测路程等有关数据,小刚特意在学校的田径跑道上,按上学的步行速度,走完100 m用了150步.
(1)小刚上学步行的平均速度是多少?小刚家和少年宫之间、少年宫和学校之间的路程分别是多少?
(2)下午4:00,小刚从学校出发,以45 m/min的速度行走,按上学时的原路回家,在未到少年宫300 m处与同伴玩了半小时后,赶紧以110 m/min的速度回家,中途没有再停留.问:
①小刚到家的时间是下午几时?
②小刚回家过程中,离家的路程s(m)与时间t(min)之间的函
数关系如图,请写出点B的坐标,并求出线段CD所在直线的
函数关系式.
【解析】(1)小刚每分钟走1200÷10=120(步),每步是
100÷150= (m),120× =80(m/min),所以小刚上学的步行速度
是80 m/min.小刚家和少年宫之间的路程是80×10=800(m).
少年宫和学校之间的路程是80×(25-10)=1200(m).
(2)① (min),所以小刚到家的时间是下午5:00.
②小刚从学校出发,以45 m/min的速度行走到离少年宫300 m处时实际走了900 m,用时 min,此时小刚离家1100m,所以点B的坐标是(20,1100).线段CD表示小刚与同伴玩了30 min后,回家的这个时间段中离家的路程s(m)与行走时间t(min)之间的函数关系,由路程与时间的关系得 即线段CD所在直线的函数关系式是s=-110t+6600(50≤t≤60).
5.已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm) 4.2 … 8.2 9.8
体温计的读数y(℃) 35.0 … 40.0 42.0
(1)求y关于x的函数关系式(不需要写出函数的定义域);
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.
第四章 一次函数
4.4一次函数的应用
第1课时
超出起步价,怎么算?
超出免托运,怎么算?
1.了解两个条件可以确定一个一次函数,一个条件可
以确定一个正比例函数.
3.能够根据实际问题抽象出数学模型并利用一次函数
解决实际问题.
2.能根据所给信息(图象、表格等)确定一次函数的
表达式.
1.已知一个正比例函数,它的图象经过点(-1,2),则该函数表达式是_____.
-2
O
【例题讲解】
2.有同学画了如图一条直线的图象,
你知道该函数的表达式吗?
y
x
0
-3
2
6
8
-3
【跟踪训练】
【解析】
即当所挂物体的质量为4 kg时弹簧的长度为16.5cm。
A
1.已知四条直线y=kx-3,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或-2 B.2或-1
C.3 D.4
B
A.-1 B.1 C.5 D.-5
B
1
5.根据如图所示的条件,写出直线的表达式 ___________.
6.某同学在做放水实验时,记录下池中水量y(m3)与放水时间 x (h)之间有如下对应关系 :
x … 2 4 6 …
y … 15 12 9 6 …
(1)按规律把表格填写完整:
(2)池中原有水__m3.
8
18
7.已知一次函数y=kx-4,当x=2时,y=-3.
(1)求一次函数的关系式.
(2)将该函数的图象向上平行移动6个单位,求平行移动后的图象与x轴交点的坐标.
解决一次函数的表达式问题,一般采用待定系数法,这是初中数学的一种重要的方法 .
【规律方法】
本节课我们主要学习了根据已知条件,如何求函数的表达式:
1.设函数表达式.
3.解方程,求k,b.
第四章 一次函数
4.4一次函数的应用
第2课时
观察与思考
20
0
40
60
80
100
单位:cm
观察下图,你能发现它们三条函数直线之间的差别吗?
1.掌握两个一次函数图象的应用.(重点)
2.能利用函数图象解决数学问题.(难点)
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
引例:l1 反映了某公司产品的销售收入与销售量的关系,根据图意填空:
l1
当销售量为2吨时,销售收入= 元,
2000
销售收入
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了公司产品的销售收入与销售量的关系.
销售收入
l1对应的函数表达式是 ,
y=1000x
l1
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2 反映了公司产品的销售成本与销售量的关系
销售成本
l2对应的函数表达式是 .
y=500x+2000
l2
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
当销售成本为4500元时,销售量= 吨;
5
销售成本
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(1)当销售量为6吨时,销售收入= 元,
销售成本= 元, 利润= 元.
6000
5000
(2)当销售量为 时,销售收入等于销售成本.
4吨
销售收入
销售成本
1000
销售收入和销售成本都是4000元.
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(3)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本).
大于4吨
小于4吨
销售收入
销售成本
5
6
1
2
3
P
你还有什么发现?
7
8
【例题1】
假设甲、乙两人保持现有的速度,根据图象回答下列问题
(1)哪条线表示甲到观景台1的路程与追赶时间之间的关系
(2)甲和乙哪个人的速度快
(3)30min内甲能否追上乙
(4)到达观景台3后道路分岔,甲能否在到达观景台3前追上乙
(5)设l1与l2对应的两个一次函数分别为s=k1t+b1与s=k2t+b2,k1,
k2的实际意义各是什么 甲、乙两人的速度各是多少
1.A城有肥料200 t,B城有肥料300 t,现要把这些肥料全部运往C,D两乡.从A城往C,D两乡运肥料费用分别为每吨20元和25元;从B城往C,D两乡运肥料费用分别为每吨15元和24元.现C乡需要肥料240 t,D乡需要肥料260 t.怎样调运总运费最少?
分析:可以发现:A──C,A──D,B──C,B──D运肥料共涉及4个变量.它们都是影响总运费的变量.然而它们之间又有一定的必然联系,只要确定其中一个量,其余三个量也就随之确定.
【跟踪训练】
设A──C,x t,则:
由于A城有肥料200 t:A─D,(200-x) t.
由于C乡需要240 t:B─C,(240-x) t.
由于D乡需要260 t:B─D,(260-200+x) t.
那么,各段运输费用为:
A──C 20x
A──D 25(200-x)
B──C 15(240-x)
B──D 24(60+x)
【解析】
设总运费为y,y与x的关系为:
y=20x+25(200-x)+15(240-x)+24(60+x).
即:y=4x+10040 (0≤x≤200)
由关系式或图象都可看出,当x=0时,y值最小为10040.
因此,从A城运往C乡0t,运往D乡200 t;
从B城运往C乡240 t,运往D乡60t .
此时总运费最少,为10040元.
通过本课时的学习,需要我们掌握:
1.通过函数图象获取信息,发展形象思维.
2.利用函数图象解决简单的实际问题,发展数学的应用能力.
1. 如图,过点Q(0,3.5)的一次函数的图象与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是( )
A.3x-2y+3.5=0 B.3x-2y-3.5=0
C.3x-2y+7=0 D.3x+2y-7=0
【解析】设一次函数的关系式为y=kx+b,
又因为过Q(0,3.5),P(1,2)两点,
代入得y=-1.5x+3.5,整理得3x+2y-7=0.
D
2.甲、乙两人准备在一段长为1200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s,起跑前乙在起点,甲在乙前面100 m处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙
两人之间的距离y(m)与时间t(s)的函数图象是( )
【解析】设乙追上甲用x s,则6x-4x=100,x=50,乙跑完
全程用时1200÷6=200(s).
C
3. 一次函数y= x+4分别交x轴、y轴于A,B两点,在x轴上取
一点C,使△ABC为等腰三角形,则这样的点C有几个
【解析】在△ABC中,使△ABC为等腰三角形有AB=AC=
时,C点的坐标为(-4- ,0);( -4 ,0).当
AB=BC时,C点的坐标有(4,0);当AC=BC时,C点的坐标
有(0,0),故有4个.
4.小刚上午7:30从家里出发步行上学,途经少年宫时走了1200步,用时10 min,到达学校的时间是7:55.为了估测路程等有关数据,小刚特意在学校的田径跑道上,按上学的步行速度,走完100 m用了150步.
(1)小刚上学步行的平均速度是多少?小刚家和少年宫之间、少年宫和学校之间的路程分别是多少?
(2)下午4:00,小刚从学校出发,以45 m/min的速度行走,按上学时的原路回家,在未到少年宫300 m处与同伴玩了半小时后,赶紧以110 m/min的速度回家,中途没有再停留.问:
①小刚到家的时间是下午几时?
②小刚回家过程中,离家的路程s(m)与时间t(min)之间的函
数关系如图,请写出点B的坐标,并求出线段CD所在直线的
函数关系式.
【解析】(1)小刚每分钟走1200÷10=120(步),每步是
100÷150= (m),120× =80(m/min),所以小刚上学的步行速度
是80 m/min.小刚家和少年宫之间的路程是80×10=800(m).
少年宫和学校之间的路程是80×(25-10)=1200(m).
(2)① (min),所以小刚到家的时间是下午5:00.
②小刚从学校出发,以45 m/min的速度行走到离少年宫300 m处时实际走了900 m,用时 min,此时小刚离家1100m,所以点B的坐标是(20,1100).线段CD表示小刚与同伴玩了30 min后,回家的这个时间段中离家的路程s(m)与行走时间t(min)之间的函数关系,由路程与时间的关系得 即线段CD所在直线的函数关系式是s=-110t+6600(50≤t≤60).
5.已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm) 4.2 … 8.2 9.8
体温计的读数y(℃) 35.0 … 40.0 42.0
(1)求y关于x的函数关系式(不需要写出函数的定义域);
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.
同课章节目录
