5.4 二元一次方程与一次函数 课件 (第1---2课时,41张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.4 二元一次方程与一次函数 课件 (第1---2课时,41张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 21:26:15 | ||
图片预览








文档简介
(共41张PPT)
第五章 二元一次方程组
5.4 二元一次方程与一次函数(第1课时)
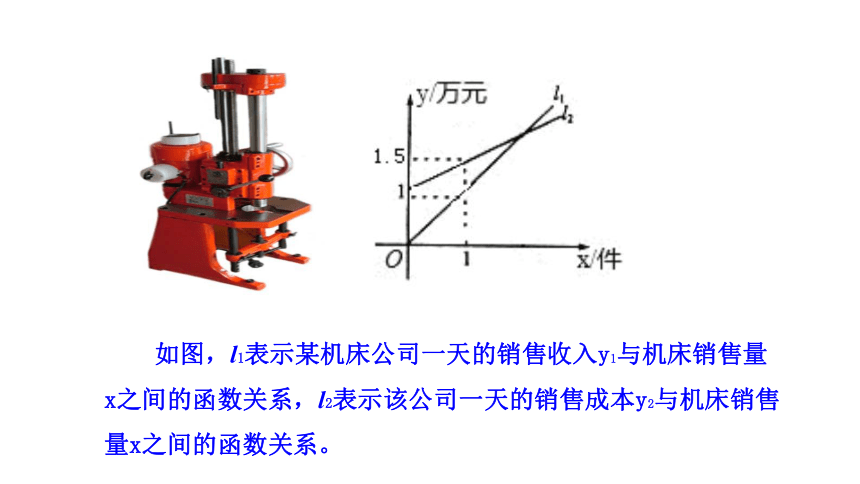
如图,l1表示某机床公司一天的销售收入y1与机床销售量x之间的函数关系,l2表示该公司一天的销售成本y2与机床销售量x之间的函数关系。
1.理解二元一次方程和一次函数的关系;掌握二元一次方程组和对应的两条直线之间的关系;掌握二元一次方程组的图象解法.
2.理解作函数图象的方法与代数方法各自的特点. 进一步理解方程与函数的联系.
1.方程x+y=5的解有多少个 写出其中的几个.
2.在平面直角坐标系中分别描出以这些解为坐标的点,它们在一次
函数y=5-x的图象上吗?
3.在一次函数y=5-x的图象上任取一点,它的坐标适合方程x+y=5吗? 4.以方程 x+y=5的解为坐标的所有点组成的图象与一次函数y=5
-x的图象相同吗?
问题:
(1)由以上四个问题你能得到什么结论?
(2)你能把上面的结论推广到一般情况吗?
以二元一次方程kx-y=-b(k≠0)的解为坐标的点组成的图象与一次函数y=kx+b的图象相同.
思考:
结论:
2.交点的坐标与方程组
1.在同一平面直角坐标系内分别画出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗
的解有什么关系?
问题:
每个二元一次方程组都对应两个一次函数(两条直线),从“数”的角度看,解方程组就相当于考虑自变量为何值时两个函数值相等,以及这个函数值是何值.从“形”的角度看,解方程组就相当于确定两条直线的交点坐标,即两条直线交点横、纵坐标就是二元一次方程组的解.
结论:
【例1】用作图象的方法解方程组:
(1)书写步骤:
A 二元一次方程化一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.
注 意
【例题】
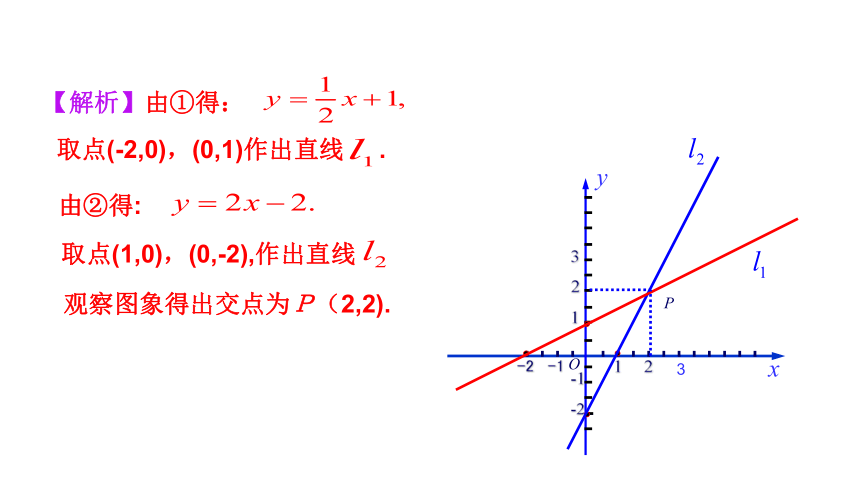
取点(-2,0),(0,1)作出直线 .
由②得:
【解析】由①得:
取点(1,0),(0,-2),作出直线
观察图象得出交点为P(2,2).
x
3
2
1
-1
-2
y
-2
2
-1
1
3
O
P
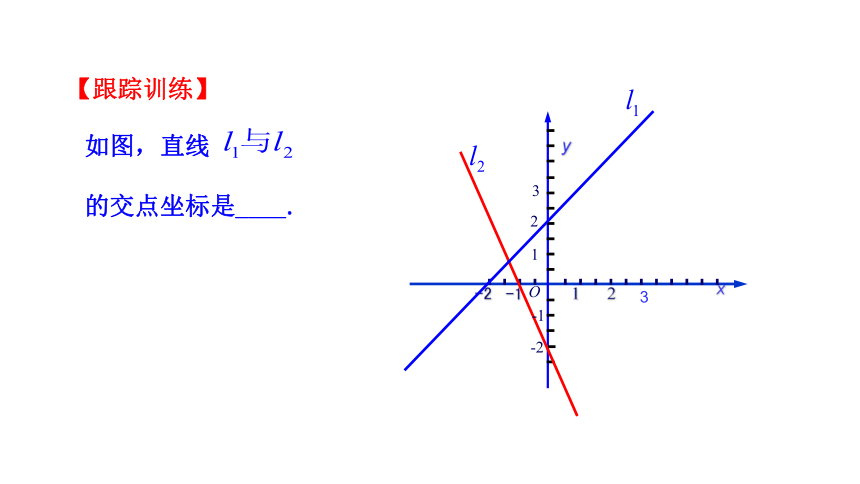
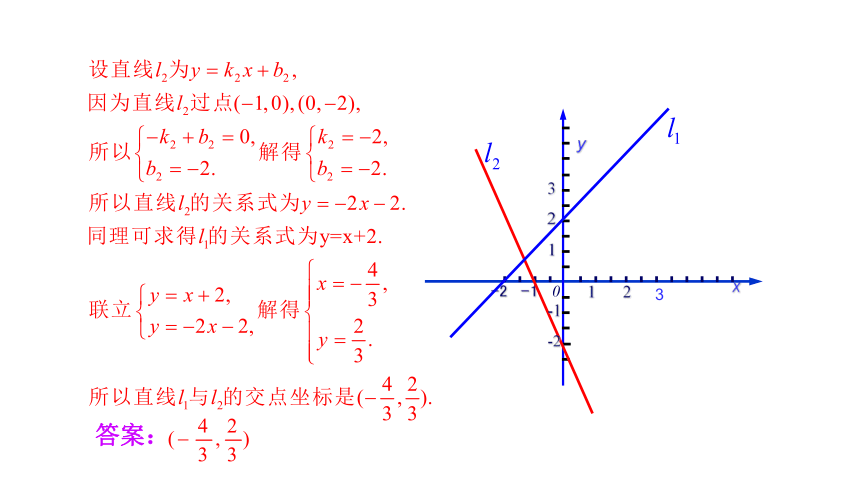
如图,直线
的交点坐标是____.
【跟踪训练】
x
y
-2
2
-1
1
3
O
1
2
3
-1
-2
答案:
x
y
-2
2
-1
0
1
3
3
2
1
-1
-2
二元一次方程组有哪些解法?
消元法
二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解.
正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.
图象法
是一种代数方法
【规律方法】
【跟踪训练】
1.用图象法解方程组
【解析】 由x+y=2,得y=-x+2;
由2x+y=1,得y=-2x+1.
在同一直角坐标系中作出一
次函数y=-x+2的图象l1和
y=-2x+1的图象l2,如图,
观察图象,得l1,l2的交点为P(-1,3).
所以方程组
的解是
2 .如图,观察图象,确定方
程组 的解.
【解析】由x-y=-1可得 y=x+1;
由x-y=2可得 y=x-2.
观察图象,可知两直线平行,无交点,
这说明方程组
无解.
1.二元一次方程组除了可以利用代入法和加减法进行消元求解外,还可以利用图象法得到它的近似解.
2.体现了数学的数形结合思想.
A.4 B.5 C.6 D.7
C
1
-9
解析:
3.求两条直线y=3x-2与 y=-2x+4和x轴所围成的三角形的面积.
O
x
y
1
2
3
4
5
6
-1
-2
-1
-2
1
2
3
4
5
6
y=3x-2
y=-2x+4
4.如图,两条直线 的交点坐标可以看作哪个方程组的解?
解析:
3
-1
2
-3
x
y
0
5.两直线
的交点坐标为( )
A.(—2,3) B.(2,—3)
C.(—2,—3) D.(2,3)
D
6.直线y=2x+b与x轴的交点坐标是
(2,0),则关于x的方程2x+b=0的解是x=______.
2
第五章 二元一次方程组
5.4 二元一次方程与一次函数(第2课时)
1.用二元一次方程组求实际问题的一次函数表达式.
2.掌握利用二元一次方程组确定一次函数的表达式.进一步理解方程与函数的联系.
函数表达式
y=kx+b
满足条件的两点
(x1, y1), (x2, y2)
一次函数的图象直线l
选取
解出
画出
选取
用二元一次方程组求一次函数表达式
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
A,B 两地相距100 km,甲、乙两人骑车分别从A,B两地相向而行.假设他们都匀速骑行,则他们各自与A地之间的距离s(单位:km)都是骑车时间t (单位:h)的一次函数.骑行1 h乙距离A地80 km; 2h后甲距离A地30 km. 经过多长时间两人相遇
直线型图表示
80 km
乙
1h
议一议
2h,30 km
甲
B
A
你明白他的想法吗?
用他的方法做一做!
O
1
2
3
t/h
s/km
100
80
60
40
20
如图,可以分别画出两人 s 与t 之间关系的图象,找出交点的横坐标就行了!
小亮
甲
乙
小明
对于乙,s 是t的一次函数,可以设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,从而确定乙的s与t 之间的关系式.
同样可以求出甲的s与t之间的关系式.
再联立这两个关系式,求解方程组就行了!
你明白他的想法吗?用他的方法做一做!
消去 s
骑行1 h乙距离A地80 km,即乙的速度是
20 km/h; 骑行2 h甲距离A 地 30 km, 故甲的速度是 15 km/h,由此可以求出甲、乙两人的速度和 ……
小颖
你明白她的想法吗?
用她的方法做一做!
t =
小明
小亮
小颖
用画图象的方法可以直观地获得结果,但往往难以获得准确的结果,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量需购买行李票,且行李费y(单位:元)是行李质量x(单位:kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的关系式;
(2)每名乘客最多可免费携带多少千克的行李?
【例题】
【解析】(1)设y=kx+b(k≠0) . 根据题意,得
解得
所以每名乘客最多可免费携带30 kg的行李.
1.某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应缴水费y(单位:元)与月用水量x(单位:t)的函数关系如图所示.
【跟踪训练】
O
y(元)
x(t)
15
20
27
39
(2)若某用户十月份用水量为10 t,则应缴水费多少元?若该用户十一月份缴水费51元,则该用户该月用水多少吨?
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,
解得
①
当x>15时,设y=mx+n,根据题意,可得方程组
解得
②
(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.
1.利用二元一次方程组求一次函数表达式的一般步骤:
a.用含字母的系数设出一次函数的表达式 ;
b.将已知条件代入上述表达式中得k,b的二元一次方程组;
c.解这个二元一次方程组得k,b,进而得到一次函数的表达式.
2.体现了数学的数形结合思想.
1. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
2.判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
∴
【解析】设过A,B两点的直线的表达式为
y=kx+b,由题意可知,
∴过A,B 两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2,
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在
同一条直线上.
3.甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(单位:m)与修筑时间x(单位:h)的函数图象的一部分.请根据图中信息,解答下列问题:
(1)直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式
;
(2)直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式
.
2
5
10
50
70
x
y
甲
乙
O
(m)
(h)
y=10x
y=20x-30
4.温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关系近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
【解析】
5.在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少
解:设购买量y与单价x的函数解析式为y=kx+b,
∵当x=1000时 y = 800;当x=2000时y = 700,
∴
800k + b = 1000
700k + b = 2000
{
解得:
b =9000
因此,购买量y与单价x的函数解析式为 y =-10x + 9000
当 y = 400时得, -10 x + 9000 =400,
∴ x =860.
答:当客户购买400kg,单价是860元.
{
第五章 二元一次方程组
5.4 二元一次方程与一次函数(第1课时)
如图,l1表示某机床公司一天的销售收入y1与机床销售量x之间的函数关系,l2表示该公司一天的销售成本y2与机床销售量x之间的函数关系。
1.理解二元一次方程和一次函数的关系;掌握二元一次方程组和对应的两条直线之间的关系;掌握二元一次方程组的图象解法.
2.理解作函数图象的方法与代数方法各自的特点. 进一步理解方程与函数的联系.
1.方程x+y=5的解有多少个 写出其中的几个.
2.在平面直角坐标系中分别描出以这些解为坐标的点,它们在一次
函数y=5-x的图象上吗?
3.在一次函数y=5-x的图象上任取一点,它的坐标适合方程x+y=5吗? 4.以方程 x+y=5的解为坐标的所有点组成的图象与一次函数y=5
-x的图象相同吗?
问题:
(1)由以上四个问题你能得到什么结论?
(2)你能把上面的结论推广到一般情况吗?
以二元一次方程kx-y=-b(k≠0)的解为坐标的点组成的图象与一次函数y=kx+b的图象相同.
思考:
结论:
2.交点的坐标与方程组
1.在同一平面直角坐标系内分别画出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗
的解有什么关系?
问题:
每个二元一次方程组都对应两个一次函数(两条直线),从“数”的角度看,解方程组就相当于考虑自变量为何值时两个函数值相等,以及这个函数值是何值.从“形”的角度看,解方程组就相当于确定两条直线的交点坐标,即两条直线交点横、纵坐标就是二元一次方程组的解.
结论:
【例1】用作图象的方法解方程组:
(1)书写步骤:
A 二元一次方程化一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.
注 意
【例题】
取点(-2,0),(0,1)作出直线 .
由②得:
【解析】由①得:
取点(1,0),(0,-2),作出直线
观察图象得出交点为P(2,2).
x
3
2
1
-1
-2
y
-2
2
-1
1
3
O
P
如图,直线
的交点坐标是____.
【跟踪训练】
x
y
-2
2
-1
1
3
O
1
2
3
-1
-2
答案:
x
y
-2
2
-1
0
1
3
3
2
1
-1
-2
二元一次方程组有哪些解法?
消元法
二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解.
正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.
图象法
是一种代数方法
【规律方法】
【跟踪训练】
1.用图象法解方程组
【解析】 由x+y=2,得y=-x+2;
由2x+y=1,得y=-2x+1.
在同一直角坐标系中作出一
次函数y=-x+2的图象l1和
y=-2x+1的图象l2,如图,
观察图象,得l1,l2的交点为P(-1,3).
所以方程组
的解是
2 .如图,观察图象,确定方
程组 的解.
【解析】由x-y=-1可得 y=x+1;
由x-y=2可得 y=x-2.
观察图象,可知两直线平行,无交点,
这说明方程组
无解.
1.二元一次方程组除了可以利用代入法和加减法进行消元求解外,还可以利用图象法得到它的近似解.
2.体现了数学的数形结合思想.
A.4 B.5 C.6 D.7
C
1
-9
解析:
3.求两条直线y=3x-2与 y=-2x+4和x轴所围成的三角形的面积.
O
x
y
1
2
3
4
5
6
-1
-2
-1
-2
1
2
3
4
5
6
y=3x-2
y=-2x+4
4.如图,两条直线 的交点坐标可以看作哪个方程组的解?
解析:
3
-1
2
-3
x
y
0
5.两直线
的交点坐标为( )
A.(—2,3) B.(2,—3)
C.(—2,—3) D.(2,3)
D
6.直线y=2x+b与x轴的交点坐标是
(2,0),则关于x的方程2x+b=0的解是x=______.
2
第五章 二元一次方程组
5.4 二元一次方程与一次函数(第2课时)
1.用二元一次方程组求实际问题的一次函数表达式.
2.掌握利用二元一次方程组确定一次函数的表达式.进一步理解方程与函数的联系.
函数表达式
y=kx+b
满足条件的两点
(x1, y1), (x2, y2)
一次函数的图象直线l
选取
解出
画出
选取
用二元一次方程组求一次函数表达式
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
A,B 两地相距100 km,甲、乙两人骑车分别从A,B两地相向而行.假设他们都匀速骑行,则他们各自与A地之间的距离s(单位:km)都是骑车时间t (单位:h)的一次函数.骑行1 h乙距离A地80 km; 2h后甲距离A地30 km. 经过多长时间两人相遇
直线型图表示
80 km
乙
1h
议一议
2h,30 km
甲
B
A
你明白他的想法吗?
用他的方法做一做!
O
1
2
3
t/h
s/km
100
80
60
40
20
如图,可以分别画出两人 s 与t 之间关系的图象,找出交点的横坐标就行了!
小亮
甲
乙
小明
对于乙,s 是t的一次函数,可以设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,从而确定乙的s与t 之间的关系式.
同样可以求出甲的s与t之间的关系式.
再联立这两个关系式,求解方程组就行了!
你明白他的想法吗?用他的方法做一做!
消去 s
骑行1 h乙距离A地80 km,即乙的速度是
20 km/h; 骑行2 h甲距离A 地 30 km, 故甲的速度是 15 km/h,由此可以求出甲、乙两人的速度和 ……
小颖
你明白她的想法吗?
用她的方法做一做!
t =
小明
小亮
小颖
用画图象的方法可以直观地获得结果,但往往难以获得准确的结果,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量需购买行李票,且行李费y(单位:元)是行李质量x(单位:kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的关系式;
(2)每名乘客最多可免费携带多少千克的行李?
【例题】
【解析】(1)设y=kx+b(k≠0) . 根据题意,得
解得
所以每名乘客最多可免费携带30 kg的行李.
1.某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应缴水费y(单位:元)与月用水量x(单位:t)的函数关系如图所示.
【跟踪训练】
O
y(元)
x(t)
15
20
27
39
(2)若某用户十月份用水量为10 t,则应缴水费多少元?若该用户十一月份缴水费51元,则该用户该月用水多少吨?
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,
解得
①
当x>15时,设y=mx+n,根据题意,可得方程组
解得
②
(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.
1.利用二元一次方程组求一次函数表达式的一般步骤:
a.用含字母的系数设出一次函数的表达式 ;
b.将已知条件代入上述表达式中得k,b的二元一次方程组;
c.解这个二元一次方程组得k,b,进而得到一次函数的表达式.
2.体现了数学的数形结合思想.
1. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
2.判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
∴
【解析】设过A,B两点的直线的表达式为
y=kx+b,由题意可知,
∴过A,B 两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2,
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在
同一条直线上.
3.甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(单位:m)与修筑时间x(单位:h)的函数图象的一部分.请根据图中信息,解答下列问题:
(1)直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式
;
(2)直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式
.
2
5
10
50
70
x
y
甲
乙
O
(m)
(h)
y=10x
y=20x-30
4.温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关系近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
【解析】
5.在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少
解:设购买量y与单价x的函数解析式为y=kx+b,
∵当x=1000时 y = 800;当x=2000时y = 700,
∴
800k + b = 1000
700k + b = 2000
{
解得:
b =9000
因此,购买量y与单价x的函数解析式为 y =-10x + 9000
当 y = 400时得, -10 x + 9000 =400,
∴ x =860.
答:当客户购买400kg,单价是860元.
{
同课章节目录
