5.5三元一次方程组 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.5三元一次方程组 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 871.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 21:38:20 | ||
图片预览





文档简介
(共23张PPT)
第五章 二元一次方程组
*5.5 三元一次方程组
1.理解三元一次方程组的概念.
2.能解简单的三元一次方程组.
复习引入
1.解二元一次方程组有哪几种方法?
2.解二元一次方程组的基本思路是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化二元为一元
化归转化思想
代入消元法和加减消元法
消元法
思考:若含有3个未知数的方程组如何求解?
问题引入
三个小动物年龄之和为26岁
流氓兔比加菲猫大1岁
流氓兔年龄的2倍加上米老鼠的年龄之和比加菲猫大18岁
三元一次方程(组)的概念
知识点1
求三个小动物
的年龄
互动探究
问题1:题中有几个未知量?你能找出哪些等量关系?
未知量:
流氓兔的年龄
加菲猫的年龄
米老鼠的年龄
每一个未知量都用一个字母表示
x岁
y岁
z岁
三个未知数(元)
等量关系:
(1)流氓兔的年龄+加菲猫的年龄+米老鼠的年龄=26
(2)流氓兔的年龄-1=加菲猫的年龄
(3)2×流氓兔的年龄+米老鼠的年龄=加菲猫的年龄+18
用方程表示等量关系.
x+y+z=26.
x-1=y.
2x+z=y+18.
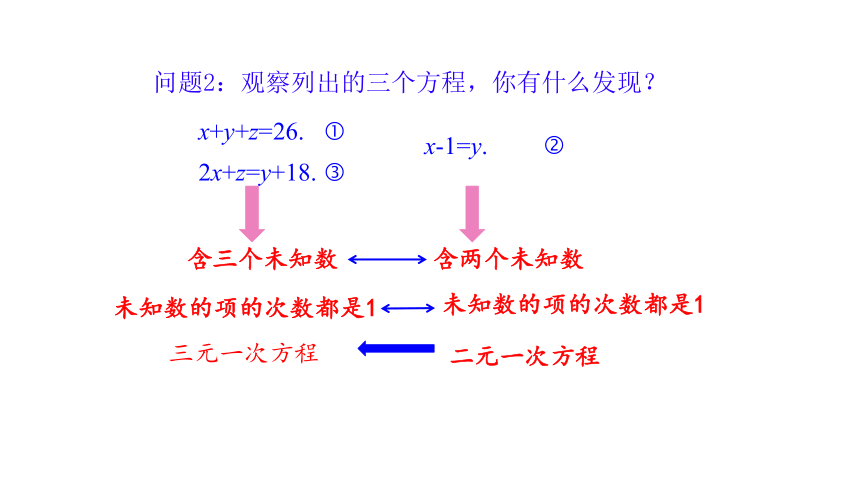
问题2:观察列出的三个方程,你有什么发现?
x+y+z=26.
x-1=y.
2x+z=y+18.
二元一次方程
三元一次方程
含两个未知数
未知数的项的次数都是1
含三个未知数
未知数的项的次数都是1
因三个小动物的年龄必须同时满足上述三个方程,故将三个方程联立在一起.
x+y+z=26.
x-1=y.
2x+z=y+18.
在这个方程组中,共含有三个未知数的三个一次方程所组成的一组方程,叫作三元一次方程组.
练一练:下列方程组不是三元一次方程组的是 ( )
A.
B.
C.
D.
D
[注意] 组成三元一次方程组的三个一次方程中,不一定要求每一个一次方程都含有三个未知数.
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫作这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
三元一次方程组的解
知识点2
典例精析
例1:解方程组
解:由方程②得 x=y+1 ④
把④分别代入①③得
2y+z=22 ⑤
3y-z=18 ⑥
解由⑤⑥组成的二元一次方程组,得
y=8,z=6
把y=8代入④,得x=9
所以原方程组的解是
x=9
y=8
z=6
类似二元一次方程组的“消元”,把“三元”化成“二元”.
总结归纳
解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
例2:在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2
c=-5,
a=3,
b=-2,
c=-5.
因此
例3 幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素.现有一批营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A,B,C三种食物,下表给出的是每份(50g)食物A,B,C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
三元一次方程组的应用
知识点3
(1)如果设食谱中A,B,C三种食物各为x,y,z份,请列出方程组,使得A,B,C三种食物中所含的营养量刚好满足幼儿营养标准中的要求.
(2)解该三元一次方程组,求出满足要求的A,B,C的份数.
解:(1)设食谱中A,B,C三种食物各x,y,z份,由该食谱中包含35单位的铁、70单位的钙和35单位的维生素,得方程组
- ×4, - ,得
⑤
④
⑤+④,得
⑥
④
通过回代,得 z=2,y=1,x=2.
答:该食谱中包含A种食物2份,B种食物1份,C种食物2份.
三元一次方程组
三元一次方程组的概念
三元一次方程组的解法
1.解方程组 ,则x=_____,
y=______,z=_______.
x+y-z=11,
y+z-x=5,
z+x-y=1.
①
②
③
【解析】通过观察未知数的系数,可采取① +②求出y, ②+ ③求出z,最后再将y与z的值代入任何一个方程求出x即可.
6
8
3
2.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
解析: 通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z=25,所以x+y+z=5.
D
3.若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b c的值.
解:因为三个非负数的和等于0,所以每个非负数都为0.
可得方程组 解得
4.一个三位数,十位上的数字是个位上的数字的 ,百位上的数字与十位上的数字之和比个位上的数字大1.将百位与个位上的数字对调后得到的新三位数比原三位数大495,求原三位数.
解:设原三位数百位、十位、个位上的数字分别为x,y,z.由题意,得
解得
答:原三位数是368.
5.三元一次方程组
x+y=10
y+z=20 的解是___________.
z+x=40
6.已知三元一次方程组
x+y=3
y+z=4,则x+y+z=__.
x+z=5
6
x=15
y= 5
z=25
第五章 二元一次方程组
*5.5 三元一次方程组
1.理解三元一次方程组的概念.
2.能解简单的三元一次方程组.
复习引入
1.解二元一次方程组有哪几种方法?
2.解二元一次方程组的基本思路是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化二元为一元
化归转化思想
代入消元法和加减消元法
消元法
思考:若含有3个未知数的方程组如何求解?
问题引入
三个小动物年龄之和为26岁
流氓兔比加菲猫大1岁
流氓兔年龄的2倍加上米老鼠的年龄之和比加菲猫大18岁
三元一次方程(组)的概念
知识点1
求三个小动物
的年龄
互动探究
问题1:题中有几个未知量?你能找出哪些等量关系?
未知量:
流氓兔的年龄
加菲猫的年龄
米老鼠的年龄
每一个未知量都用一个字母表示
x岁
y岁
z岁
三个未知数(元)
等量关系:
(1)流氓兔的年龄+加菲猫的年龄+米老鼠的年龄=26
(2)流氓兔的年龄-1=加菲猫的年龄
(3)2×流氓兔的年龄+米老鼠的年龄=加菲猫的年龄+18
用方程表示等量关系.
x+y+z=26.
x-1=y.
2x+z=y+18.
问题2:观察列出的三个方程,你有什么发现?
x+y+z=26.
x-1=y.
2x+z=y+18.
二元一次方程
三元一次方程
含两个未知数
未知数的项的次数都是1
含三个未知数
未知数的项的次数都是1
因三个小动物的年龄必须同时满足上述三个方程,故将三个方程联立在一起.
x+y+z=26.
x-1=y.
2x+z=y+18.
在这个方程组中,共含有三个未知数的三个一次方程所组成的一组方程,叫作三元一次方程组.
练一练:下列方程组不是三元一次方程组的是 ( )
A.
B.
C.
D.
D
[注意] 组成三元一次方程组的三个一次方程中,不一定要求每一个一次方程都含有三个未知数.
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫作这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
三元一次方程组的解
知识点2
典例精析
例1:解方程组
解:由方程②得 x=y+1 ④
把④分别代入①③得
2y+z=22 ⑤
3y-z=18 ⑥
解由⑤⑥组成的二元一次方程组,得
y=8,z=6
把y=8代入④,得x=9
所以原方程组的解是
x=9
y=8
z=6
类似二元一次方程组的“消元”,把“三元”化成“二元”.
总结归纳
解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
例2:在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2
c=-5,
a=3,
b=-2,
c=-5.
因此
例3 幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素.现有一批营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A,B,C三种食物,下表给出的是每份(50g)食物A,B,C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
三元一次方程组的应用
知识点3
(1)如果设食谱中A,B,C三种食物各为x,y,z份,请列出方程组,使得A,B,C三种食物中所含的营养量刚好满足幼儿营养标准中的要求.
(2)解该三元一次方程组,求出满足要求的A,B,C的份数.
解:(1)设食谱中A,B,C三种食物各x,y,z份,由该食谱中包含35单位的铁、70单位的钙和35单位的维生素,得方程组
- ×4, - ,得
⑤
④
⑤+④,得
⑥
④
通过回代,得 z=2,y=1,x=2.
答:该食谱中包含A种食物2份,B种食物1份,C种食物2份.
三元一次方程组
三元一次方程组的概念
三元一次方程组的解法
1.解方程组 ,则x=_____,
y=______,z=_______.
x+y-z=11,
y+z-x=5,
z+x-y=1.
①
②
③
【解析】通过观察未知数的系数,可采取① +②求出y, ②+ ③求出z,最后再将y与z的值代入任何一个方程求出x即可.
6
8
3
2.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
解析: 通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z=25,所以x+y+z=5.
D
3.若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b c的值.
解:因为三个非负数的和等于0,所以每个非负数都为0.
可得方程组 解得
4.一个三位数,十位上的数字是个位上的数字的 ,百位上的数字与十位上的数字之和比个位上的数字大1.将百位与个位上的数字对调后得到的新三位数比原三位数大495,求原三位数.
解:设原三位数百位、十位、个位上的数字分别为x,y,z.由题意,得
解得
答:原三位数是368.
5.三元一次方程组
x+y=10
y+z=20 的解是___________.
z+x=40
6.已知三元一次方程组
x+y=3
y+z=4,则x+y+z=__.
x+z=5
6
x=15
y= 5
z=25
同课章节目录
