6.1平均数与方差 课件(第1---2课时,45张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 6.1平均数与方差 课件(第1---2课时,45张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:00:32 | ||
图片预览







文档简介
(共45张PPT)
第六章 数据的分析
6.1 平均数与方差(第1课时)
1.掌握众数、算术平均数和加权平均数的概念,会求一组数据的众数、算术平均数和加权平均数.
2.会用众数、算术平均数、加权平均数解决实际生活中的问题.
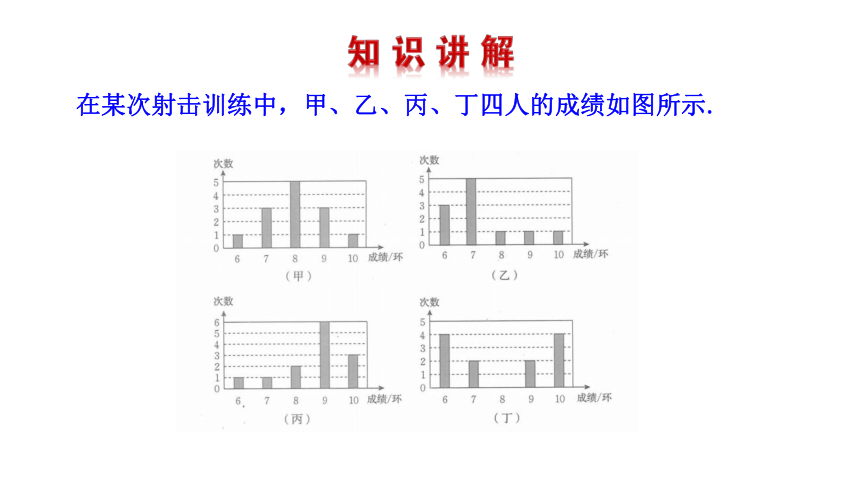
在某次射击训练中,甲、乙、丙、丁四人的成绩如图所示.
(1)观察统计图,甲的哪个射击成绩出现的次数最多?其他选手呢?
(2)不计算,请你尝试判断谁的射击成绩最好。你是怎么判断的?
(3)算一算,验证你的判断是否正确.
一组数据中出现次数最多的那个数据叫作这组数据的众数.
一组数据中所有数据之和除以这组数据的个数,就得到这组数据的算术平均数,简称平均数.平均数是刻画一组数据集中趋势的一项指标,反映了一组数据的“中心”.
众数、算术平均数
知识点1
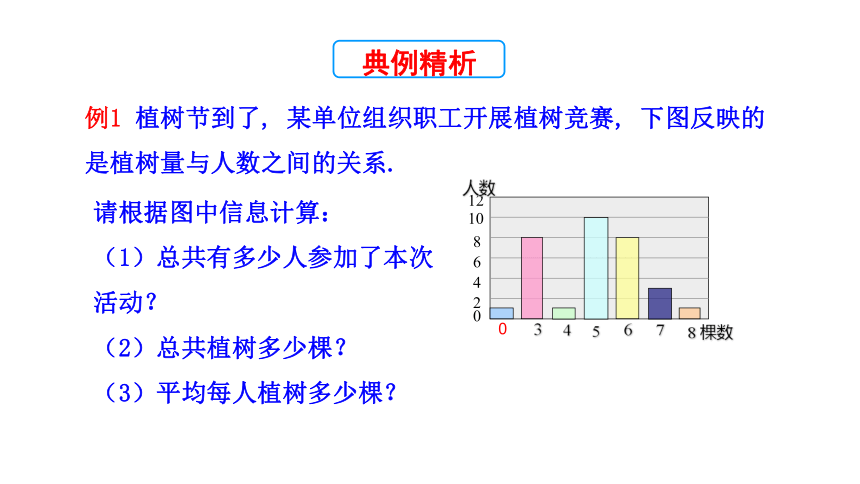
例1 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
典例精析
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人)
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
(3)平均每人植树 (棵)
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
某班级为了解同学年龄情况,做了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,他们的平均年龄约为14岁.
练一练
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往根据各个数据的“重要程度”赋一个“权”.
一起来看看下面的例子
加权平均数
知识点2
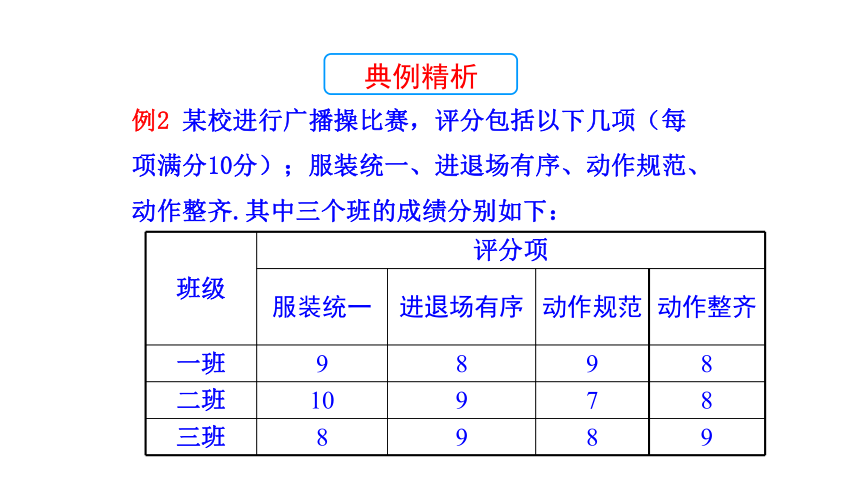
例2 某校进行广播操比赛,评分包括以下几项(每项满分10分);服装统一、进退场有序、动作规范、动作整齐.其中三个班的成绩分别如下:
班级 评分项
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
典例精析
(1)如果将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
解:一班的成绩为9×10%+8×20%+9×30%+8×40%=8.4(分).
二班的成绩为10×10%+9×20%+7×30%+8×40%=8.1(分).
三班的成绩为8×10%+9×20%+8×30%+9×40%=8.6(分).
所以,三班的成绩最高.
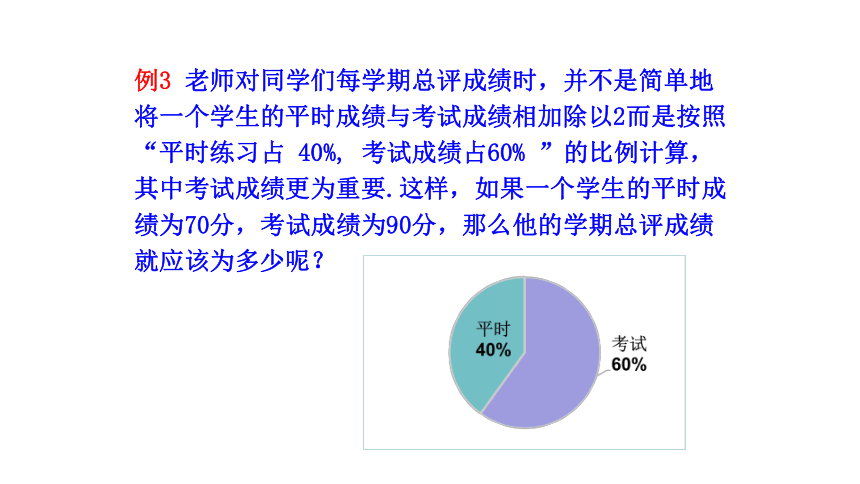
例3 老师对同学们每学期总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2而是按照“平时练习占 40%, 考试成绩占60% ”的比例计算,其中考试成绩更为重要.这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩就应该为多少呢?
解:
该同学的学期总评成绩是:
70×30%
=82(分)
+
90×60%
加权平均数
权 重
权重的意义:
各个数据在该组数据中所占有的不同重要性的反映.
加权平均数的意义:
按各个数据的权重来反映该组数据的总体平均大小情况.
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫作这n个数的加权平均数.
知识要点
众数与平均数
算术平均数
加权平均数
众数
2. 若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A.(x+y)/2 B.(x+y)/(m+n)
C.(mx+ny)/(x+y) D.(mx+ny)/(m+n)
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
D
D
3.抽样调查了某校30位女生所穿鞋子的尺码,数据如下(单位:码):
35
尺码 33 34 35 36 37
人数 7 6 15 1 1
这组数据的众数是 .
4.为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,得分情况如表所示:
得分 6 7 8 9 10
人数 4 10 15 11 10则抽取的居民得分的众数和平均数分别为 .
5.某中学举行歌咏比赛,六位评委对某位选手打分如下:77,82,78,95,83,75,去掉一个最高分和一个最低分后的平均分是 分
8分和8.26分
80
6.一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听、说、读、写的成绩按照3∶3∶2∶2的
比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81,
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
第六章 数据的分析
6.1 平均数与方差(第2课时)
学校篮球联赛开始了
刘教练
选 我
选 我
教练的烦恼
刘教练到我班选拔一名篮球队员,刘教练对陈方楷和李霖东两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队 员 第 1次 第2次 第3次 第4次 第5次
李霖东 7 8 8 8 9
陈方楷 10 6 10 6 8
(1)请求出以上两组数据的平均数、众数;
(3)若要选一个投篮稳定的队员,选谁更好?
(2)用复式折线统计图表示上述数据;
1.理解离差平方和、方差、标准差、组内离差平方和的意义.
2.会计算一组简单数据的离差平方和、方差、标准差、组内离差平方和.
甲与丁的射击成绩如图所示,他们的平均成绩都是8环,两个人的射击表现一样吗?你对甲、丁的射击表现有什么评价?
离差平方和、方差与标准差
知识点
(1)你觉得谁发挥得更稳定?你的理由是什么?
(2)你能设法通过计算说明两人的成绩的稳定程度吗?与同伴进行交流.
在统计学里,数据的离散程度可以用离差平方和、方差或标准差等统计量来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
其中, 是x1,x2,……,xn的平均数,s2是方差,而标准差就是方差的算术平方根.
离差平方和是各个数据与它们平均数之差的平方和.
即
一般而言,一组数据的方差或标准差越小,这组数据就越稳定.
例1:计算图中甲射击成绩的标准差(结果精确到0.01环)
/次序
例2: 小明和小兵两人参加体育项目训练,近期的五次测试成绩如下表所示.谁的成绩较为稳定?为什么?
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
测试成绩
测试次数
1 2 3 4 5 求离差平方和
小明 每次测试成绩 10 14 13 12 13
(每次成绩-
平均成绩)2 5.76 2.56 0.36 0.16 0.36 9.2
小兵 每次测试成绩 11 11 15 14 11
(每次成绩-
平均成绩)2 1.96 1.96 6.76 2.56 1.96 15.2
计算可得:
小明5次测试成绩的标准差为1.84;
小兵5次测试成绩的标准差为3.04.
所以根据结果小明的成绩比较稳定.
方法拓展
任取一个基准数
将原数据减去 ,得到一组新数据
求新数据的方差
1
2
3
求一组较大数据的方差,有如下简便计算方法:
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②甲班成绩的波动比乙班大.上述结论正确的有 .
班级 参加人数 方差 平均数
甲 55 191 135
乙 55 110 135
①②
做一做
例 10个苹果的直径如图所示
(1)若想把这 10个苹果分成两组,使每组苹果的“个头”差不多,你想怎么分 说说你分组的理由。
(2)一般情况下,如果想把一组数据分成若干组,使每组组内的数据差距不大,且组与组之间的数据差别明显,那么你认为应遵循怎样的分组原则 与同伴进行交流。
在统计学里,分组的方法有很多,其中较常用的方法是使“组内离差平方和达到最小”。多组数据的组内离差平方和是指每组数据的离差平方和的和。
按照“组内离差平方和达到最小”的方法,把图中的10个苹果按直径大小分成两组.
解:将10个数据由小到大排序:
65,69,70,75,76,76,78,80,80,81
把10个数据分成两组,共有9种情况:第一组9个数据{65},第二组9个数据{69,…,81};第一组2个数据{65,69},第二组8个数据{70,…81};……;第一组9个数据{65,69},第二组一个数据{81}.
以第2种分组情况为例,计算组内离差平方和.其中,第一组有2个数据{65,69},这2个数据的平均数是67,故第一组数据的组内离差平方和S =(65-67) +(69-67) =8;第二组有8个数据{70,75,76,76,78,80,80,81},这8个数据的平均数是77,故第二组数据的组内离差平方和S =(70-77) +(75-77) +…+(81-77) =90.
因此第2种分组情况的组内离差平方和S=S +S =8+90=98.
同理计算其他8种分组情况的组内离差平方和,结果如下:
计算结果表明,第3种情况的组内离差平方和最小.因此把10个苹果按直径大小分成的两组是{65,69,70},{75,76,76,78,80,80,81}.
数据的离散程度
方差
标准差
组内离差平方和
离差平方和
2.在样本方差的计算公式
中, 数字10 表示________ ,数字20表示 ______.
样本容量
平均数
1.把数据2,8,10,4,12按大小顺序分成两组,能使“组内离差平方和达到最小”的是( )
A.{2},{4,8,10,12}
B.{2,4},{8,10,12}
C.{2,4,8},{10,12}
D.{2,4,8,10},{12}
B
3.某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是 =3.6, =4.6, =6.3, =7.3,则这4名同学3次数学成绩最稳定的是( )
A.甲 B.乙
C.丙 D.丁
A
4.数据-2,-1,0,1,2的方差是___,标准差是___ .
5.五个数1,3, ,5,8的平均数是4,则 =_____,这五个数的方差_____.
2
3
5.6
6. 甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
所以是乙台编织机出的产品的波动性较小.
=(7+10+8+8+7)÷5=8
=(8+9+7+9+7)÷5=8
第六章 数据的分析
6.1 平均数与方差(第1课时)
1.掌握众数、算术平均数和加权平均数的概念,会求一组数据的众数、算术平均数和加权平均数.
2.会用众数、算术平均数、加权平均数解决实际生活中的问题.
在某次射击训练中,甲、乙、丙、丁四人的成绩如图所示.
(1)观察统计图,甲的哪个射击成绩出现的次数最多?其他选手呢?
(2)不计算,请你尝试判断谁的射击成绩最好。你是怎么判断的?
(3)算一算,验证你的判断是否正确.
一组数据中出现次数最多的那个数据叫作这组数据的众数.
一组数据中所有数据之和除以这组数据的个数,就得到这组数据的算术平均数,简称平均数.平均数是刻画一组数据集中趋势的一项指标,反映了一组数据的“中心”.
众数、算术平均数
知识点1
例1 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
典例精析
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人)
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
(3)平均每人植树 (棵)
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
某班级为了解同学年龄情况,做了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,他们的平均年龄约为14岁.
练一练
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往根据各个数据的“重要程度”赋一个“权”.
一起来看看下面的例子
加权平均数
知识点2
例2 某校进行广播操比赛,评分包括以下几项(每项满分10分);服装统一、进退场有序、动作规范、动作整齐.其中三个班的成绩分别如下:
班级 评分项
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
典例精析
(1)如果将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
解:一班的成绩为9×10%+8×20%+9×30%+8×40%=8.4(分).
二班的成绩为10×10%+9×20%+7×30%+8×40%=8.1(分).
三班的成绩为8×10%+9×20%+8×30%+9×40%=8.6(分).
所以,三班的成绩最高.
例3 老师对同学们每学期总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2而是按照“平时练习占 40%, 考试成绩占60% ”的比例计算,其中考试成绩更为重要.这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩就应该为多少呢?
解:
该同学的学期总评成绩是:
70×30%
=82(分)
+
90×60%
加权平均数
权 重
权重的意义:
各个数据在该组数据中所占有的不同重要性的反映.
加权平均数的意义:
按各个数据的权重来反映该组数据的总体平均大小情况.
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫作这n个数的加权平均数.
知识要点
众数与平均数
算术平均数
加权平均数
众数
2. 若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A.(x+y)/2 B.(x+y)/(m+n)
C.(mx+ny)/(x+y) D.(mx+ny)/(m+n)
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
D
D
3.抽样调查了某校30位女生所穿鞋子的尺码,数据如下(单位:码):
35
尺码 33 34 35 36 37
人数 7 6 15 1 1
这组数据的众数是 .
4.为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,得分情况如表所示:
得分 6 7 8 9 10
人数 4 10 15 11 10则抽取的居民得分的众数和平均数分别为 .
5.某中学举行歌咏比赛,六位评委对某位选手打分如下:77,82,78,95,83,75,去掉一个最高分和一个最低分后的平均分是 分
8分和8.26分
80
6.一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听、说、读、写的成绩按照3∶3∶2∶2的
比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81,
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
第六章 数据的分析
6.1 平均数与方差(第2课时)
学校篮球联赛开始了
刘教练
选 我
选 我
教练的烦恼
刘教练到我班选拔一名篮球队员,刘教练对陈方楷和李霖东两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队 员 第 1次 第2次 第3次 第4次 第5次
李霖东 7 8 8 8 9
陈方楷 10 6 10 6 8
(1)请求出以上两组数据的平均数、众数;
(3)若要选一个投篮稳定的队员,选谁更好?
(2)用复式折线统计图表示上述数据;
1.理解离差平方和、方差、标准差、组内离差平方和的意义.
2.会计算一组简单数据的离差平方和、方差、标准差、组内离差平方和.
甲与丁的射击成绩如图所示,他们的平均成绩都是8环,两个人的射击表现一样吗?你对甲、丁的射击表现有什么评价?
离差平方和、方差与标准差
知识点
(1)你觉得谁发挥得更稳定?你的理由是什么?
(2)你能设法通过计算说明两人的成绩的稳定程度吗?与同伴进行交流.
在统计学里,数据的离散程度可以用离差平方和、方差或标准差等统计量来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
其中, 是x1,x2,……,xn的平均数,s2是方差,而标准差就是方差的算术平方根.
离差平方和是各个数据与它们平均数之差的平方和.
即
一般而言,一组数据的方差或标准差越小,这组数据就越稳定.
例1:计算图中甲射击成绩的标准差(结果精确到0.01环)
/次序
例2: 小明和小兵两人参加体育项目训练,近期的五次测试成绩如下表所示.谁的成绩较为稳定?为什么?
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
测试成绩
测试次数
1 2 3 4 5 求离差平方和
小明 每次测试成绩 10 14 13 12 13
(每次成绩-
平均成绩)2 5.76 2.56 0.36 0.16 0.36 9.2
小兵 每次测试成绩 11 11 15 14 11
(每次成绩-
平均成绩)2 1.96 1.96 6.76 2.56 1.96 15.2
计算可得:
小明5次测试成绩的标准差为1.84;
小兵5次测试成绩的标准差为3.04.
所以根据结果小明的成绩比较稳定.
方法拓展
任取一个基准数
将原数据减去 ,得到一组新数据
求新数据的方差
1
2
3
求一组较大数据的方差,有如下简便计算方法:
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②甲班成绩的波动比乙班大.上述结论正确的有 .
班级 参加人数 方差 平均数
甲 55 191 135
乙 55 110 135
①②
做一做
例 10个苹果的直径如图所示
(1)若想把这 10个苹果分成两组,使每组苹果的“个头”差不多,你想怎么分 说说你分组的理由。
(2)一般情况下,如果想把一组数据分成若干组,使每组组内的数据差距不大,且组与组之间的数据差别明显,那么你认为应遵循怎样的分组原则 与同伴进行交流。
在统计学里,分组的方法有很多,其中较常用的方法是使“组内离差平方和达到最小”。多组数据的组内离差平方和是指每组数据的离差平方和的和。
按照“组内离差平方和达到最小”的方法,把图中的10个苹果按直径大小分成两组.
解:将10个数据由小到大排序:
65,69,70,75,76,76,78,80,80,81
把10个数据分成两组,共有9种情况:第一组9个数据{65},第二组9个数据{69,…,81};第一组2个数据{65,69},第二组8个数据{70,…81};……;第一组9个数据{65,69},第二组一个数据{81}.
以第2种分组情况为例,计算组内离差平方和.其中,第一组有2个数据{65,69},这2个数据的平均数是67,故第一组数据的组内离差平方和S =(65-67) +(69-67) =8;第二组有8个数据{70,75,76,76,78,80,80,81},这8个数据的平均数是77,故第二组数据的组内离差平方和S =(70-77) +(75-77) +…+(81-77) =90.
因此第2种分组情况的组内离差平方和S=S +S =8+90=98.
同理计算其他8种分组情况的组内离差平方和,结果如下:
计算结果表明,第3种情况的组内离差平方和最小.因此把10个苹果按直径大小分成的两组是{65,69,70},{75,76,76,78,80,80,81}.
数据的离散程度
方差
标准差
组内离差平方和
离差平方和
2.在样本方差的计算公式
中, 数字10 表示________ ,数字20表示 ______.
样本容量
平均数
1.把数据2,8,10,4,12按大小顺序分成两组,能使“组内离差平方和达到最小”的是( )
A.{2},{4,8,10,12}
B.{2,4},{8,10,12}
C.{2,4,8},{10,12}
D.{2,4,8,10},{12}
B
3.某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是 =3.6, =4.6, =6.3, =7.3,则这4名同学3次数学成绩最稳定的是( )
A.甲 B.乙
C.丙 D.丁
A
4.数据-2,-1,0,1,2的方差是___,标准差是___ .
5.五个数1,3, ,5,8的平均数是4,则 =_____,这五个数的方差_____.
2
3
5.6
6. 甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
所以是乙台编织机出的产品的波动性较小.
=(7+10+8+8+7)÷5=8
=(8+9+7+9+7)÷5=8
同课章节目录
