1. 1 探索勾股定理 教案 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 1. 1 探索勾股定理 教案 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:39:09 | ||
图片预览


文档简介
第一章 勾股定理
1 探索勾股定理
【教学目标】
1.先用数格子(或割、补、拼等)后用求面积的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系.
2.会初步运用勾股定理进行简单的计算和实际运用.
3.让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和由特殊到一般的思想方法.
【重点难点】
重点:1.用面积法验证勾股定理.
2.应用勾股定理解决简单的实际问题.
难点:先用数格子(或割、补、拼等)后用求面积的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系.
【教学过程】
一、创设情境
内容:2002年国际数学家大会在我国北京召开(投影显示本届国际数学家大会的会标):会标中央的图案是一个与“勾股定理”有关的图形,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号.今天我们就来一同探索勾股定理.
二、探索归纳
1.探究活动一
内容:投影显示如下地板砖示意图,引导学生从面积的角度观察图形:
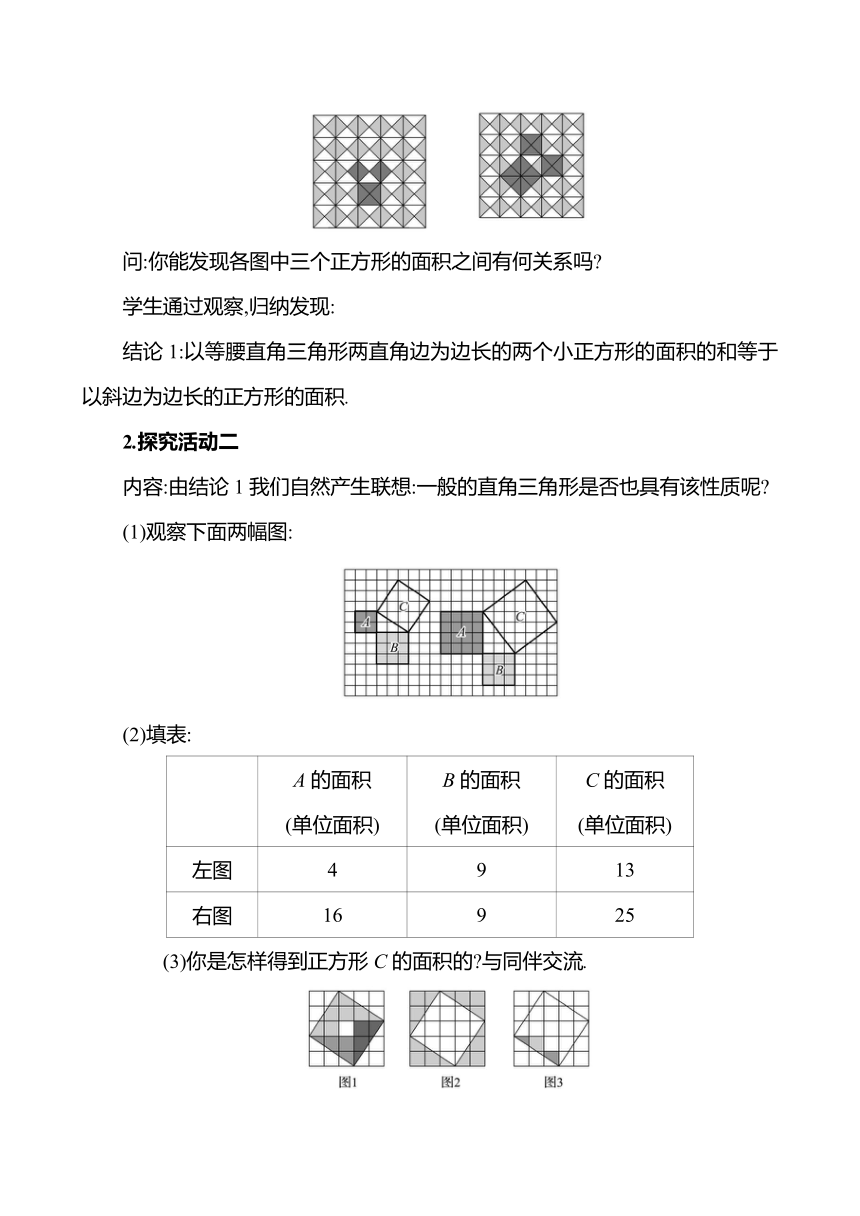
问:你能发现各图中三个正方形的面积之间有何关系吗
学生通过观察,归纳发现:
结论1:以等腰直角三角形两直角边为边长的两个小正方形的面积的和等于以斜边为边长的正方形的面积.
2.探究活动二
内容:由结论1我们自然产生联想:一般的直角三角形是否也具有该性质呢
(1)观察下面两幅图:
(2)填表:
A的面积 (单位面积) B的面积 (单位面积) C的面积 (单位面积)
左图 4 9 13
右图 16 9 25
(3)你是怎样得到正方形C的面积的 与同伴交流.
方法一:
如图1,将正方形C分割为四个全等的直角三角形和一个小正方形,SC=4××2×3+1=13.
方法二:
如图2,在正方形C外补四个全等的直角三角形,形成大正方形,用大正方形的面积减去四个直角三角形的面积,SC=52-4××2×3=13.
方法三:
如图3,正方形C中除去中间5个小正方形外,将周围部分适当拼接可成为正方形,如图3中阴影部分可拼成两个小正方形,按此拼法,SC=2×4+5=13.
(4)分析填表的数据,你发现了什么
学生通过分析数据,归纳出:
结论2:以直角三角形两直角边为边长的两个小正方形的面积的和等于以斜边为边长的正方形的面积.
3.议一议
内容:(1)你能用直角三角形的边长a,b,c来表示上图中正方形的面积吗
(2)你能发现直角三角形三边长度之间存在什么关系吗
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.2中发现的规律对这个三角形仍然成立吗
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
4.探究三:
利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形.
例题:如图所示,一棵大树在一次强烈台风中于离地面10 m处折断倒下,树顶落在离树根24 m处. 大树在折断之前高多少
三、交流反思
教师提问:
1.这一节课我们一起学习了哪些知识和思想方法
2.对这些内容你有什么体会 与同伴进行交流.
在学生自由发言的基础上,师生共同总结:
1.知识:勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
2.方法:(1) 观察—探索—猜想—验证—归纳—应用;
(2)“割、补、拼、接”法.
3.思想:(1) 特殊→一般→特殊;
(2) 数形结合思想.
四、检测反馈
1.基础巩固练习:
求下列图形中未知正方形的面积或未知边的长度(口答):
2.生活中的应用:
小明妈妈买了一部29 in(74 cm)的电视机. 小明量了电视机的屏幕后,发现屏幕只有58 cm长和46 cm宽,他觉得一定是售货员搞错了.你同意他的想法吗 你能解释这是为什么吗
五、布置作业
P8:习题1.1 1,2,3题
六、板书设计
1 探索勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
几何语言:
因为在Rt△ABC中,∠C=90°,
所以由勾股定理得:a2+b2=c2.
七、教学反思
(一)设计理念
依据“学生是学习的主体”这一理念,在探索勾股定理的整个过程中,本节课始终采用学生自主探索和与同伴合作交流相结合的方式进行主动学习.教师只在学生遇到困难时,进行引导或组织学生通过讨论来突破难点.
(二)突出重点、突破难点的策略
为了让学生在学习过程中自我发现勾股定理,本节课首先情景创设激发兴趣,再通过几个探究活动引导学生从探究等腰直角三角形这一特殊情形入手,自然过渡到探究一般直角三角形,学生通过观察图形,计算面积,分析数据,发现直角三角形三边的关系,进而得到勾股定理.
1 探索勾股定理
【教学目标】
1.先用数格子(或割、补、拼等)后用求面积的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系.
2.会初步运用勾股定理进行简单的计算和实际运用.
3.让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和由特殊到一般的思想方法.
【重点难点】
重点:1.用面积法验证勾股定理.
2.应用勾股定理解决简单的实际问题.
难点:先用数格子(或割、补、拼等)后用求面积的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系.
【教学过程】
一、创设情境
内容:2002年国际数学家大会在我国北京召开(投影显示本届国际数学家大会的会标):会标中央的图案是一个与“勾股定理”有关的图形,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号.今天我们就来一同探索勾股定理.
二、探索归纳
1.探究活动一
内容:投影显示如下地板砖示意图,引导学生从面积的角度观察图形:
问:你能发现各图中三个正方形的面积之间有何关系吗
学生通过观察,归纳发现:
结论1:以等腰直角三角形两直角边为边长的两个小正方形的面积的和等于以斜边为边长的正方形的面积.
2.探究活动二
内容:由结论1我们自然产生联想:一般的直角三角形是否也具有该性质呢
(1)观察下面两幅图:
(2)填表:
A的面积 (单位面积) B的面积 (单位面积) C的面积 (单位面积)
左图 4 9 13
右图 16 9 25
(3)你是怎样得到正方形C的面积的 与同伴交流.
方法一:
如图1,将正方形C分割为四个全等的直角三角形和一个小正方形,SC=4××2×3+1=13.
方法二:
如图2,在正方形C外补四个全等的直角三角形,形成大正方形,用大正方形的面积减去四个直角三角形的面积,SC=52-4××2×3=13.
方法三:
如图3,正方形C中除去中间5个小正方形外,将周围部分适当拼接可成为正方形,如图3中阴影部分可拼成两个小正方形,按此拼法,SC=2×4+5=13.
(4)分析填表的数据,你发现了什么
学生通过分析数据,归纳出:
结论2:以直角三角形两直角边为边长的两个小正方形的面积的和等于以斜边为边长的正方形的面积.
3.议一议
内容:(1)你能用直角三角形的边长a,b,c来表示上图中正方形的面积吗
(2)你能发现直角三角形三边长度之间存在什么关系吗
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.2中发现的规律对这个三角形仍然成立吗
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
4.探究三:
利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形.
例题:如图所示,一棵大树在一次强烈台风中于离地面10 m处折断倒下,树顶落在离树根24 m处. 大树在折断之前高多少
三、交流反思
教师提问:
1.这一节课我们一起学习了哪些知识和思想方法
2.对这些内容你有什么体会 与同伴进行交流.
在学生自由发言的基础上,师生共同总结:
1.知识:勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
2.方法:(1) 观察—探索—猜想—验证—归纳—应用;
(2)“割、补、拼、接”法.
3.思想:(1) 特殊→一般→特殊;
(2) 数形结合思想.
四、检测反馈
1.基础巩固练习:
求下列图形中未知正方形的面积或未知边的长度(口答):
2.生活中的应用:
小明妈妈买了一部29 in(74 cm)的电视机. 小明量了电视机的屏幕后,发现屏幕只有58 cm长和46 cm宽,他觉得一定是售货员搞错了.你同意他的想法吗 你能解释这是为什么吗
五、布置作业
P8:习题1.1 1,2,3题
六、板书设计
1 探索勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b,c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
几何语言:
因为在Rt△ABC中,∠C=90°,
所以由勾股定理得:a2+b2=c2.
七、教学反思
(一)设计理念
依据“学生是学习的主体”这一理念,在探索勾股定理的整个过程中,本节课始终采用学生自主探索和与同伴合作交流相结合的方式进行主动学习.教师只在学生遇到困难时,进行引导或组织学生通过讨论来突破难点.
(二)突出重点、突破难点的策略
为了让学生在学习过程中自我发现勾股定理,本节课首先情景创设激发兴趣,再通过几个探究活动引导学生从探究等腰直角三角形这一特殊情形入手,自然过渡到探究一般直角三角形,学生通过观察图形,计算面积,分析数据,发现直角三角形三边的关系,进而得到勾股定理.
同课章节目录
