2.2 平方根与立方根 教案(4课时) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 2.2 平方根与立方根 教案(4课时) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:44:11 | ||
图片预览



文档简介
2 平方根与立方根
第1课时
【教学目标】
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.了解求一个正数的算术平方根与平方是互逆的运算,会利用这个互逆运算关系求非负数的算术平方根;了解算术平方根的性质.
3.通过探究归纳,积累用逆向思维解决问题的经验,体验算术平方根的非负性.
【重点难点】
重点:1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.了解求一个正数的算术平方根与平方是互逆的运算,了解算术平方根的性质.
难点:会利用这个互逆运算关系求非负数的算术平方根.
【教学过程】
一、创设情境
方法一:问题导入
内容:上节课学习了无理数,了解到无理数产生的实际背景和引入的必要性,掌握了无理数的概念,知道有理数和无理数的区别是:有理数是有限小数或无限循环小数,无理数是无限不循环小数.比如上一节课我们做过的:由两个边长为1的小正方形,通过剪一剪,拼一拼,得到一个边长为a的大的正方形,那么有a2=2,a=________,2是有理数,而a是无理数.在前面我们学过若x2=a,则a叫x的平方,反过来x叫a的什么呢 本节课我们一起来学习.
方法二:问题导入
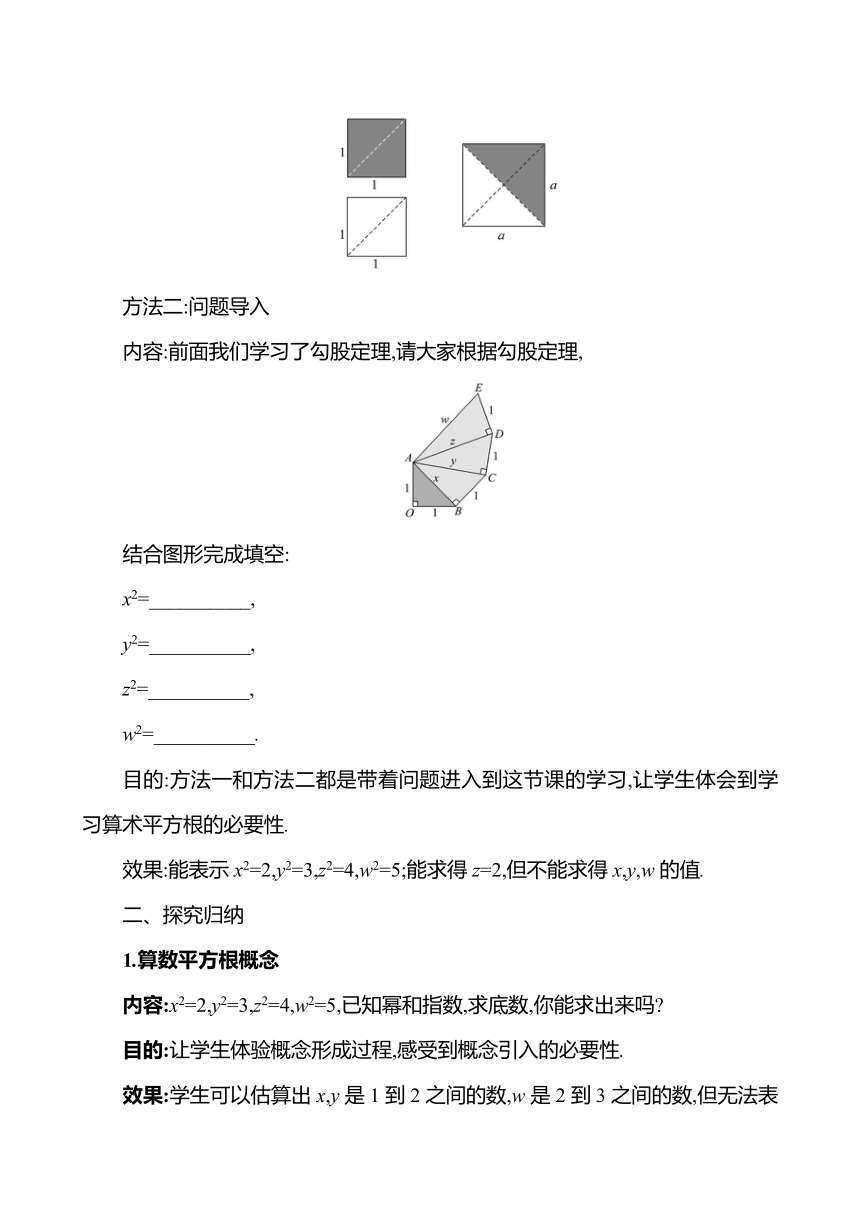
内容:前面我们学习了勾股定理,请大家根据勾股定理,
结合图形完成填空:
x2=__________,
y2=__________,
z2=__________,
w2=__________.
目的:方法一和方法二都是带着问题进入到这节课的学习,让学生体会到学习算术平方根的必要性.
效果:能表示x2=2,y2=3,z2=4,w2=5;能求得z=2,但不能求得x,y,w的值.
二、探究归纳
1.算数平方根概念
内容:x2=2,y2=3,z2=4,w2=5,已知幂和指数,求底数,你能求出来吗
目的:让学生体验概念形成过程,感受到概念引入的必要性.
效果:学生可以估算出x,y是1到2之间的数,w是2到3之间的数,但无法表示x,y,w,从而激发学生继续往下学习的兴趣,进而引入新的运算——开方.
在此基础上,明确概念:
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫作a的算术平方根,记为“”,读作“根号a”.特别地,我们规定0的算术平方根是0,即=0.
2.简单运用 巩固概念
内容:
例1:求下列各数的算术平方根:
(1) 900; (2) 1;(3);(4)14.
解:(1)因为302=900,所以900的算术平方根是30,即=30.
(2)因为12=1,所以1的算术平方根是1,即=1.
(3)因为=,所以的算术平方根是, 即=.
(4)14的算术平方根是.
3.算术平方根的性质
观察下列式子,回答问题:
=10 =3 =150
(1)由上面的算式,总结:=a,此时a的取值有什么要求
(2)()2=a成立吗 这里的a是什么数
总结算术平方根的性质
当a≥0时,=a;当a<0时,=-a.
例2:自由下落物体下落的距离s(m)与下落时间t(s)的关系为s=4.9t2.有一铁球从19.6 m高的建筑物上自由下落,到达地面需要多长时间
解:将s=19.6代入公式s=4.9t2,得t2=4,所以
t==2(s).即铁球到达地面需要2 s.
三、交流反思
内容:这节课学习的算术平方根是本章的基本概念,是为以后的学习做铺垫的.通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子中的双重非负性:一是a≥0,二是≥0.
(2)算术平方根的性质:当a≥0时,=a,()2=a;当a<0时,=-a.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
目的:依照本节课的教学目标引导学生自己小结本节课的知识要点,强化算术平方根的概念和性质.
四、检测反馈
1.(1)若一个数的算术平方根是,那么这个数是______;
(2)的算术平方根是______________________;
(3)的算术平方根是_________________;
(4)若=2,则(m+2)2=_________________.
2.求下列各数的算术平方根:
36,,15,0.64,10-4,,.
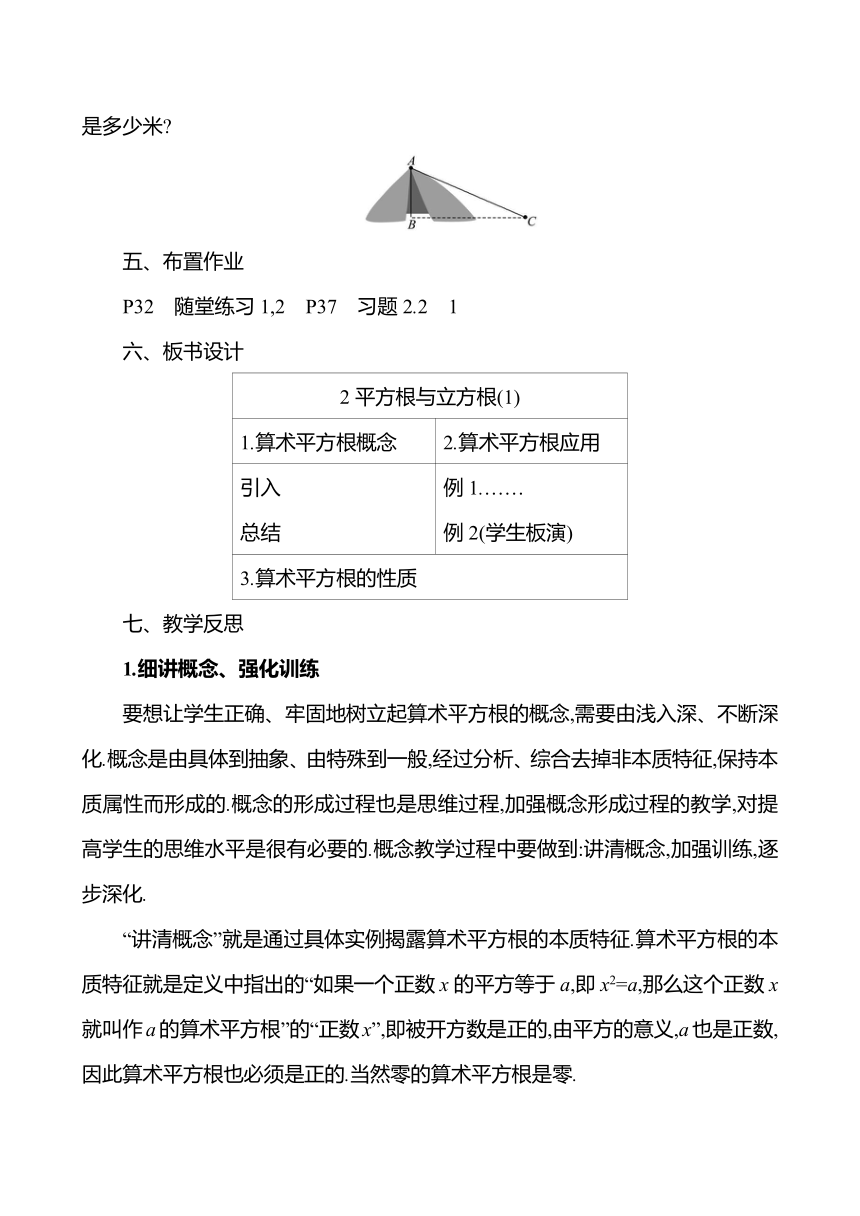
3.从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为5.5米,地面固定点C到帐篷支撑竿底部B的距离是4.5米,则帐篷支撑竿的高是多少米
五、布置作业
P32 随堂练习1,2 P37 习题2.2 1
六、板书设计
2平方根与立方根(1)
1.算术平方根概念 2.算术平方根应用
引入 总结 例1.…… 例2(学生板演)
3.算术平方根的性质
七、教学反思
1.细讲概念、强化训练
要想让学生正确、牢固地树立起算术平方根的概念,需要由浅入深、不断深化.概念是由具体到抽象、由特殊到一般,经过分析、综合去掉非本质特征,保持本质属性而形成的.概念的形成过程也是思维过程,加强概念形成过程的教学,对提高学生的思维水平是很有必要的.概念教学过程中要做到:讲清概念,加强训练,逐步深化.
“讲清概念”就是通过具体实例揭露算术平方根的本质特征.算术平方根的本质特征就是定义中指出的“如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫作a的算术平方根”的“正数x”,即被开方数是正的,由平方的意义,a也是正数,因此算术平方根也必须是正的.当然零的算术平方根是零.
“加强训练”不但指要加强求算术平方根的基本训练,使练习题达到一定的质和量,也包括书写格式的训练,如在求正数的算术平方根时,不是直接写出算术平方根,而是通过平方运算来求算术平方根,非平方数的算术平方根只能用根号来表示.
“逐步深化”是指利用算术平方根的概念和性质,把题目按不同的“梯度”组成题组,在教学的不同阶段按由浅入深的原则加以使用.
2.发展思维、适度拓展
在教学中,根据学生的实际情况,在学有余力的情况下,可以对的双重非负性的知识进行适当的拓展.
2 平方根与立方根
第2课时
【教学目标】
1.了解平方根、 开平方的概念,明确算术平方根与平方根的区别和联系.
2.进一步明确平方与开平方是互逆的运算关系.
3.通过探究归纳,积累用逆向思维解决问题的经验,体验开方运算和平方运算的互逆性.
【重点难点】
重点:了解开方与乘方是互逆的运算,会利用这个互逆运算关系求某些非负数的算术平方根和平方根.
难点:明确平方根与算术平方根的区别和联系.
【教学过程】
一、创设情境
内容:
1.到目前为止,我们已学过哪些运算 这些运算之间的关系如何 乘方有没有逆运算 平方与算术平方根之间的关系如何
2.已知正方形ABCD面积为1,则边长为__1__.将它扩展,若面积变为原来的2倍,那么它的边长为 __;若面积变为原来的3倍,则边长为 __;若面积变为原来的n倍,则边长为 __.
二、探究归纳
(一)探究新知
内容
填空
( )2=9
02=0
( )2=
(不存在)2=-4
结论1:形成概念
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫作a的平方根或二次方根.把正的平方根叫作a的算术平方根.表达式为:若x2=a,那么x叫作a的平方根, 记作±.
例如:(±4)2=16,则+4和-4都是16的平方根;即16的平方根是±4;4是16的算术平方根.
(二)探索平方与开平方的关系
给出几组具体的数据,由平方探知开平方与平方的互逆关系.
结论2:概念辨析
平方根与算术平方根的联系与区别
联系
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别
1.个数不同:一个正数有两个平方根,但只有一个算术平方根.
2.表示法不同:平方根表示为±,而算术平方根表示为.
结论3:一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根.
三、 例题和新知巩固
(一)例题示范
求下列各数的平方根:
(1)64;(2);(3)0.000 4;(4)(-25)2;(5)11.
解:(1)因为(±8)2=64,所以64的平方根是±8,即±=±8.
(2)因为=,所以的平方根为±,即±=±.
(3)因为(±0.02)2=0.000 4,所以0.000 4的平方根是±0.02,即±=±0.02.
(4)因为(±25)2=(-25)2,所以(-25)2的平方根是±25,即±=±25;
(5)11的平方根是±.
(二)思考提升
1.(-5)2的算术平方根是________,的平方根是________,的平方根是______;
2.()2=______,=______,±=______,=______;
3.=______________,当a≥0时,()2=________.
(三)巩固练习
1.下列说法正确的是________.
①-3是的平方根;②25的平方根是5;③-36的平方根是-6;④平方根等于0的数是0;⑤64的平方根是8.
2.下列说法不正确的是 ( )
A.0的平方根是0
B.-22的平方根是±2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是 ( )
A.a+1 B.
C.a2+1 D.
4.x为何值,有意义
四、交流反思
引导学生总结本课时的知识、方法.
让学生对所学的知识进行梳理,使之思路清晰,既巩固了有关知识,又培养了学生良好的学习习惯.
五、检测反馈
1. 1.5+的小数部分为a,5-的小数部分为b,求a+b的值.
2.已知实数a,b满足b2++9=6b,
①若a,b为△ABC的两边,求第三边c的取值范围.
②若a,b为△ABC的两边,第三边c等于5,求△ABC的面积.
六、布置作业
P34随堂练习 1,2,3
七、板书设计
2 平方根与立方根(2)
1.平方与开平方 2.应用
(一)探索新知 (二)平方与开平方的关系 例题.…… 练习(学生板演)
八、教学反思
(一)注重概念的形成过程,让学生在概念的形成的过程中,逐步理解所学的概念.概念是由具体到抽象、由特殊到一般,经过分析、综合去掉非本质特征,保持本质属性而形成的.概念的形成过程也是思维过程,加强概念形成过程的教学,对提高学生的思维水平是很必要的.所以在学习平方根的概念时,对正数有两个平方根学生不太容易接受,往往丢掉负的平方根,因为这与他们以前的经验不符.对此,在平方根的引入时,可多提一些具体的问题.如“9的算术平方根是3,也就是说,3的平方是9.还有其他的数,它的平方也是9吗 ”等,旨在引起学生的思考,让学生从具体的例子中抽象出初步的平方根的概念.再让学生去讨论 一个正数有几个平方根 0有几个平方根 负数呢 引导学生更深刻地理解平方根的概念,然后通过具体的求平方根的练习,巩固新学的概念.
(二)鼓励学生进行探究和交流.本节课为学生提供了有趣而富有数学含义的问题,让学生进行充分的探索和交流.如把正方形的面积不断地扩大为2倍、3倍、n倍,来引导学生充分进行交流、讨论与探索等数学活动,从中感受学习平方根的必要性.
(三)设计之中多处运用类比的方法,使学生清楚新旧知识的区别和联系.类比概念 “平方根”和“算术平方根”的区别和联系,“平方”和“开平方”运算.
(四)根据学生实际,灵活使用教材
教材上只安排了一道例题和几个想一想,为了让学生对新知巩固,增加了部分练习题,围绕“平方根”这一知识点进行各种题型的变式练习.当然,选题要有层次,有梯度.老师们在进行教学时可以根据学生的实际情况做适当的取舍.
(五)建议
根据知识结构的逻辑关系与学生的认知规律,建议教材在内容安排上将平方根置于算术平方根之前.
2 平方根与立方根
第3课时
【教学目标】
1.了解立方根的概念,会用根号表示一个数的立方根.
2.了解开立方与立方互为逆运算,会用立方运算求一个数的立方根.
3.了解立方根的性质.
【重点难点】
重点:了解立方根的概念和性质,会用三次根号表示数的立方根,用立方运算求一个数的立方根.
难点:用立方运算求一个数的立方根,区分立方根与平方根的不同.
【教学过程】
一、创设情境
要制作一种容积是8 m3的正方体包装箱,它的棱长是多少 如果容积是4m3呢
通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.在思考问题的同时,学生既感受到了数学的应用价值,激发了学习热情,又很快将问题归结为如何确定一个数,它的立方等于4,从而顺利引入新课.
二、探究归纳
提问:
(1)什么叫一个数a的平方根 如何用符号表示数a(a≥0)的平方根
(2)正数的平方根有几个 它们之间的关系是什么
负数有没有平方根 0的平方根是什么
(3)平方和开平方运算有何关系
(4)算术平方根和平方根有何区别与联系
强调:一个正数的平方根有两个,且互为相反数;负数没有平方根;0的平方根是0.
(5)为了解决前面情境中的问题,需要引入一个新的运算,你将如何定义这个新运算
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫作a的立方根(也叫作三次方根).如2是8的立方根,-3是-27的立方根,0是0的立方根.
做一做:怎样求下列括号内的数 各题中已知什么数 求什么数
(1)( )3=0.001;(2)( )3=-;
(3)( )3=0.
三、交流反思
议一议:(1)正数有几个立方根
(2)0有几个立方根
(3)负数呢
学生通过回顾上节课的学习内容,为进一步研究立方根的概念及性质做好铺垫,同时突出平方根与立方根的对比,以利于弄清两者的区别和联系.在上面的基础上明确下列内容,对知识进行梳理.
四、检测反馈
1.求下列各数的立方根: 1,-, 6,-,0.001.
2.求下列各式的值:
;;-;;;()3;
3.在下列式子中,正确的是 ( )
A.=-
B.-=-0.6
C.=-13
D.=±6
五、布置作业
P35、36随堂练习 1,2
六、板书设计
2.平方根与立方根(3)
定义及表示 例1 学生板 演练习
性质 例2
重要公式 ()3=a,=a
七、教学反思
类比学习法让学生省时省力,在学习新知的同时巩固已学的知识,通过新旧对比更好地掌握知识.为此,本节课让学生应用类比法顺理成章地学习立方根的概念、性质、运算.同样在学生以后的数学学习中,可以通过三角形类比四边形、五边形……
2 平方根与立方根
第4课时
【教学目标】
1.会估算一个无理数的大致范围,比较两个无理数的大小,会利用估算解决一些简单的实际问题.
2.经历实际问题的解决过程和平方根、立方根的估算过程,发展估算意识和数感.
【重点难点】
重点:估计一个无理数的大致范围.
难点:通过估算比较两个数的大小.
【教学过程】
一、创设情境
由修建环保公园的实际问题情境引出本节课的学习内容——公园有多宽.
某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400 000平方米.此时公园的宽是多少 长是多少
给出这个问题情境,先让学生凭感觉说出公园的长和宽分别是多少.
给出引导问题:公园的宽有1 000米吗 (没有)那么怎么计算出公园的长和宽.
解:设公园的宽为x米,则它的长为2x米,由题意得:x·2x=400 000,2x2=
400 000,x=.
那么=
从现实情境引入,一方面让学生初步建立数感,另一方面让学生体会生活中的数学从而激发学习的积极性.
二、探究归纳
内容:
1.探究一个无理数估算结果的合理性.
2.学会估算一个无理数的大致范围.
例1:(1)下列结果正确吗 你是怎样判断的 与同伴交流.
①≈20 ;②≈0.3;
③≈500;④≈96.
解:这些结果都不正确.
怎样估算一个无理数的范围
你能估算它们的大小吗 说出你的方法.
①;②;③; ④.
(①②误差小于0.1;③误差小于10;④误差小于1)
解:≈6.3 ;≈0.9;
≈310 ;≈9.
(同伴间进行交流,教师适时引导.在解决问题的同时引导学生对解决方法进行总结,和学生一起归纳出估算的方法.)
(2)尝试用计算器求上述各式的值,检验你估算的准确性.
例2:比较与的大小.
解:与的分母相同,只要比较他们的分子就可以了,因为>2,所以-1>1,>.
例3:给出新的问题情境——画能挂上去吗
生活表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,
(1)他的顶端最多能到达多高(保留到0.1)
(2)现在如果请一个同学利用这个梯子在墙高5.9米的地方张贴一幅宣传画,他能办到吗
三、交流反思
学方根与立方根之后安排本节内容,目的很明确,就是要让学生体会如何运用这些知识去解决实际问题,体会到数学的实用价值,并逐步在今后的学习中有意识地运用估算的方法解决生活中的问题,发展学生的估算意识和数感.
尝试使用计算器进行数据的开平方和开立方运算,熟悉计算器按键,通过具体操作,使学生熟悉利用计算器求平方根和立方根的技能,激发学生的学习兴趣.
四、检测反馈
1.估算下列数的大小:
(1)(误差小于0.1);(2)(误差小于1).
2.通过估算,比较下面各数的大小:
(1)与.(2)与3.85.
3.一个人一生平均要引用的液体总量大约为40立方米,如果用圆柱形的容器(底面直径等于高)来装这些液体,这个容器大概有多高(误差小于1米)
五、布置作业
P39习题2.2 16,17,18
六、板书设计
2.平方根与立方根(4)
情境引入 活动探究 例1 例2 例3 巩固练习
七、教学反思
本节课的教学中选取了“修建环保公园”的问题情境引入,与学生平时的生活密切联系,容易把学生的积极性调动起来.在探究估算方法的时候,教师要注重适时的引导,以免让学生无从下手.在教学中要多鼓励学生用自己的语言表达他们的想法,在估算的过程中多给予适当的引导和评价,让学生逐步把握估算的方法,找到解决问题的信心.作为教师,一定要尊重学生的个体差异,满足多样化的学习需要,鼓励探究方式、表达方式和解题方法的多样化.
在教学过程中一定要让学生体会估算的实用价值,了解到“数学既来源与生活,又回归到生活为生活服务”.
第1课时
【教学目标】
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.了解求一个正数的算术平方根与平方是互逆的运算,会利用这个互逆运算关系求非负数的算术平方根;了解算术平方根的性质.
3.通过探究归纳,积累用逆向思维解决问题的经验,体验算术平方根的非负性.
【重点难点】
重点:1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.了解求一个正数的算术平方根与平方是互逆的运算,了解算术平方根的性质.
难点:会利用这个互逆运算关系求非负数的算术平方根.
【教学过程】
一、创设情境
方法一:问题导入
内容:上节课学习了无理数,了解到无理数产生的实际背景和引入的必要性,掌握了无理数的概念,知道有理数和无理数的区别是:有理数是有限小数或无限循环小数,无理数是无限不循环小数.比如上一节课我们做过的:由两个边长为1的小正方形,通过剪一剪,拼一拼,得到一个边长为a的大的正方形,那么有a2=2,a=________,2是有理数,而a是无理数.在前面我们学过若x2=a,则a叫x的平方,反过来x叫a的什么呢 本节课我们一起来学习.
方法二:问题导入
内容:前面我们学习了勾股定理,请大家根据勾股定理,
结合图形完成填空:
x2=__________,
y2=__________,
z2=__________,
w2=__________.
目的:方法一和方法二都是带着问题进入到这节课的学习,让学生体会到学习算术平方根的必要性.
效果:能表示x2=2,y2=3,z2=4,w2=5;能求得z=2,但不能求得x,y,w的值.
二、探究归纳
1.算数平方根概念
内容:x2=2,y2=3,z2=4,w2=5,已知幂和指数,求底数,你能求出来吗
目的:让学生体验概念形成过程,感受到概念引入的必要性.
效果:学生可以估算出x,y是1到2之间的数,w是2到3之间的数,但无法表示x,y,w,从而激发学生继续往下学习的兴趣,进而引入新的运算——开方.
在此基础上,明确概念:
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫作a的算术平方根,记为“”,读作“根号a”.特别地,我们规定0的算术平方根是0,即=0.
2.简单运用 巩固概念
内容:
例1:求下列各数的算术平方根:
(1) 900; (2) 1;(3);(4)14.
解:(1)因为302=900,所以900的算术平方根是30,即=30.
(2)因为12=1,所以1的算术平方根是1,即=1.
(3)因为=,所以的算术平方根是, 即=.
(4)14的算术平方根是.
3.算术平方根的性质
观察下列式子,回答问题:
=10 =3 =150
(1)由上面的算式,总结:=a,此时a的取值有什么要求
(2)()2=a成立吗 这里的a是什么数
总结算术平方根的性质
当a≥0时,=a;当a<0时,=-a.
例2:自由下落物体下落的距离s(m)与下落时间t(s)的关系为s=4.9t2.有一铁球从19.6 m高的建筑物上自由下落,到达地面需要多长时间
解:将s=19.6代入公式s=4.9t2,得t2=4,所以
t==2(s).即铁球到达地面需要2 s.
三、交流反思
内容:这节课学习的算术平方根是本章的基本概念,是为以后的学习做铺垫的.通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子中的双重非负性:一是a≥0,二是≥0.
(2)算术平方根的性质:当a≥0时,=a,()2=a;当a<0时,=-a.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
目的:依照本节课的教学目标引导学生自己小结本节课的知识要点,强化算术平方根的概念和性质.
四、检测反馈
1.(1)若一个数的算术平方根是,那么这个数是______;
(2)的算术平方根是______________________;
(3)的算术平方根是_________________;
(4)若=2,则(m+2)2=_________________.
2.求下列各数的算术平方根:
36,,15,0.64,10-4,,.
3.从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为5.5米,地面固定点C到帐篷支撑竿底部B的距离是4.5米,则帐篷支撑竿的高是多少米
五、布置作业
P32 随堂练习1,2 P37 习题2.2 1
六、板书设计
2平方根与立方根(1)
1.算术平方根概念 2.算术平方根应用
引入 总结 例1.…… 例2(学生板演)
3.算术平方根的性质
七、教学反思
1.细讲概念、强化训练
要想让学生正确、牢固地树立起算术平方根的概念,需要由浅入深、不断深化.概念是由具体到抽象、由特殊到一般,经过分析、综合去掉非本质特征,保持本质属性而形成的.概念的形成过程也是思维过程,加强概念形成过程的教学,对提高学生的思维水平是很有必要的.概念教学过程中要做到:讲清概念,加强训练,逐步深化.
“讲清概念”就是通过具体实例揭露算术平方根的本质特征.算术平方根的本质特征就是定义中指出的“如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫作a的算术平方根”的“正数x”,即被开方数是正的,由平方的意义,a也是正数,因此算术平方根也必须是正的.当然零的算术平方根是零.
“加强训练”不但指要加强求算术平方根的基本训练,使练习题达到一定的质和量,也包括书写格式的训练,如在求正数的算术平方根时,不是直接写出算术平方根,而是通过平方运算来求算术平方根,非平方数的算术平方根只能用根号来表示.
“逐步深化”是指利用算术平方根的概念和性质,把题目按不同的“梯度”组成题组,在教学的不同阶段按由浅入深的原则加以使用.
2.发展思维、适度拓展
在教学中,根据学生的实际情况,在学有余力的情况下,可以对的双重非负性的知识进行适当的拓展.
2 平方根与立方根
第2课时
【教学目标】
1.了解平方根、 开平方的概念,明确算术平方根与平方根的区别和联系.
2.进一步明确平方与开平方是互逆的运算关系.
3.通过探究归纳,积累用逆向思维解决问题的经验,体验开方运算和平方运算的互逆性.
【重点难点】
重点:了解开方与乘方是互逆的运算,会利用这个互逆运算关系求某些非负数的算术平方根和平方根.
难点:明确平方根与算术平方根的区别和联系.
【教学过程】
一、创设情境
内容:
1.到目前为止,我们已学过哪些运算 这些运算之间的关系如何 乘方有没有逆运算 平方与算术平方根之间的关系如何
2.已知正方形ABCD面积为1,则边长为__1__.将它扩展,若面积变为原来的2倍,那么它的边长为 __;若面积变为原来的3倍,则边长为 __;若面积变为原来的n倍,则边长为 __.
二、探究归纳
(一)探究新知
内容
填空
( )2=9
02=0
( )2=
(不存在)2=-4
结论1:形成概念
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫作a的平方根或二次方根.把正的平方根叫作a的算术平方根.表达式为:若x2=a,那么x叫作a的平方根, 记作±.
例如:(±4)2=16,则+4和-4都是16的平方根;即16的平方根是±4;4是16的算术平方根.
(二)探索平方与开平方的关系
给出几组具体的数据,由平方探知开平方与平方的互逆关系.
结论2:概念辨析
平方根与算术平方根的联系与区别
联系
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别
1.个数不同:一个正数有两个平方根,但只有一个算术平方根.
2.表示法不同:平方根表示为±,而算术平方根表示为.
结论3:一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根.
三、 例题和新知巩固
(一)例题示范
求下列各数的平方根:
(1)64;(2);(3)0.000 4;(4)(-25)2;(5)11.
解:(1)因为(±8)2=64,所以64的平方根是±8,即±=±8.
(2)因为=,所以的平方根为±,即±=±.
(3)因为(±0.02)2=0.000 4,所以0.000 4的平方根是±0.02,即±=±0.02.
(4)因为(±25)2=(-25)2,所以(-25)2的平方根是±25,即±=±25;
(5)11的平方根是±.
(二)思考提升
1.(-5)2的算术平方根是________,的平方根是________,的平方根是______;
2.()2=______,=______,±=______,=______;
3.=______________,当a≥0时,()2=________.
(三)巩固练习
1.下列说法正确的是________.
①-3是的平方根;②25的平方根是5;③-36的平方根是-6;④平方根等于0的数是0;⑤64的平方根是8.
2.下列说法不正确的是 ( )
A.0的平方根是0
B.-22的平方根是±2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是 ( )
A.a+1 B.
C.a2+1 D.
4.x为何值,有意义
四、交流反思
引导学生总结本课时的知识、方法.
让学生对所学的知识进行梳理,使之思路清晰,既巩固了有关知识,又培养了学生良好的学习习惯.
五、检测反馈
1. 1.5+的小数部分为a,5-的小数部分为b,求a+b的值.
2.已知实数a,b满足b2++9=6b,
①若a,b为△ABC的两边,求第三边c的取值范围.
②若a,b为△ABC的两边,第三边c等于5,求△ABC的面积.
六、布置作业
P34随堂练习 1,2,3
七、板书设计
2 平方根与立方根(2)
1.平方与开平方 2.应用
(一)探索新知 (二)平方与开平方的关系 例题.…… 练习(学生板演)
八、教学反思
(一)注重概念的形成过程,让学生在概念的形成的过程中,逐步理解所学的概念.概念是由具体到抽象、由特殊到一般,经过分析、综合去掉非本质特征,保持本质属性而形成的.概念的形成过程也是思维过程,加强概念形成过程的教学,对提高学生的思维水平是很必要的.所以在学习平方根的概念时,对正数有两个平方根学生不太容易接受,往往丢掉负的平方根,因为这与他们以前的经验不符.对此,在平方根的引入时,可多提一些具体的问题.如“9的算术平方根是3,也就是说,3的平方是9.还有其他的数,它的平方也是9吗 ”等,旨在引起学生的思考,让学生从具体的例子中抽象出初步的平方根的概念.再让学生去讨论 一个正数有几个平方根 0有几个平方根 负数呢 引导学生更深刻地理解平方根的概念,然后通过具体的求平方根的练习,巩固新学的概念.
(二)鼓励学生进行探究和交流.本节课为学生提供了有趣而富有数学含义的问题,让学生进行充分的探索和交流.如把正方形的面积不断地扩大为2倍、3倍、n倍,来引导学生充分进行交流、讨论与探索等数学活动,从中感受学习平方根的必要性.
(三)设计之中多处运用类比的方法,使学生清楚新旧知识的区别和联系.类比概念 “平方根”和“算术平方根”的区别和联系,“平方”和“开平方”运算.
(四)根据学生实际,灵活使用教材
教材上只安排了一道例题和几个想一想,为了让学生对新知巩固,增加了部分练习题,围绕“平方根”这一知识点进行各种题型的变式练习.当然,选题要有层次,有梯度.老师们在进行教学时可以根据学生的实际情况做适当的取舍.
(五)建议
根据知识结构的逻辑关系与学生的认知规律,建议教材在内容安排上将平方根置于算术平方根之前.
2 平方根与立方根
第3课时
【教学目标】
1.了解立方根的概念,会用根号表示一个数的立方根.
2.了解开立方与立方互为逆运算,会用立方运算求一个数的立方根.
3.了解立方根的性质.
【重点难点】
重点:了解立方根的概念和性质,会用三次根号表示数的立方根,用立方运算求一个数的立方根.
难点:用立方运算求一个数的立方根,区分立方根与平方根的不同.
【教学过程】
一、创设情境
要制作一种容积是8 m3的正方体包装箱,它的棱长是多少 如果容积是4m3呢
通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.在思考问题的同时,学生既感受到了数学的应用价值,激发了学习热情,又很快将问题归结为如何确定一个数,它的立方等于4,从而顺利引入新课.
二、探究归纳
提问:
(1)什么叫一个数a的平方根 如何用符号表示数a(a≥0)的平方根
(2)正数的平方根有几个 它们之间的关系是什么
负数有没有平方根 0的平方根是什么
(3)平方和开平方运算有何关系
(4)算术平方根和平方根有何区别与联系
强调:一个正数的平方根有两个,且互为相反数;负数没有平方根;0的平方根是0.
(5)为了解决前面情境中的问题,需要引入一个新的运算,你将如何定义这个新运算
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫作a的立方根(也叫作三次方根).如2是8的立方根,-3是-27的立方根,0是0的立方根.
做一做:怎样求下列括号内的数 各题中已知什么数 求什么数
(1)( )3=0.001;(2)( )3=-;
(3)( )3=0.
三、交流反思
议一议:(1)正数有几个立方根
(2)0有几个立方根
(3)负数呢
学生通过回顾上节课的学习内容,为进一步研究立方根的概念及性质做好铺垫,同时突出平方根与立方根的对比,以利于弄清两者的区别和联系.在上面的基础上明确下列内容,对知识进行梳理.
四、检测反馈
1.求下列各数的立方根: 1,-, 6,-,0.001.
2.求下列各式的值:
;;-;;;()3;
3.在下列式子中,正确的是 ( )
A.=-
B.-=-0.6
C.=-13
D.=±6
五、布置作业
P35、36随堂练习 1,2
六、板书设计
2.平方根与立方根(3)
定义及表示 例1 学生板 演练习
性质 例2
重要公式 ()3=a,=a
七、教学反思
类比学习法让学生省时省力,在学习新知的同时巩固已学的知识,通过新旧对比更好地掌握知识.为此,本节课让学生应用类比法顺理成章地学习立方根的概念、性质、运算.同样在学生以后的数学学习中,可以通过三角形类比四边形、五边形……
2 平方根与立方根
第4课时
【教学目标】
1.会估算一个无理数的大致范围,比较两个无理数的大小,会利用估算解决一些简单的实际问题.
2.经历实际问题的解决过程和平方根、立方根的估算过程,发展估算意识和数感.
【重点难点】
重点:估计一个无理数的大致范围.
难点:通过估算比较两个数的大小.
【教学过程】
一、创设情境
由修建环保公园的实际问题情境引出本节课的学习内容——公园有多宽.
某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400 000平方米.此时公园的宽是多少 长是多少
给出这个问题情境,先让学生凭感觉说出公园的长和宽分别是多少.
给出引导问题:公园的宽有1 000米吗 (没有)那么怎么计算出公园的长和宽.
解:设公园的宽为x米,则它的长为2x米,由题意得:x·2x=400 000,2x2=
400 000,x=.
那么=
从现实情境引入,一方面让学生初步建立数感,另一方面让学生体会生活中的数学从而激发学习的积极性.
二、探究归纳
内容:
1.探究一个无理数估算结果的合理性.
2.学会估算一个无理数的大致范围.
例1:(1)下列结果正确吗 你是怎样判断的 与同伴交流.
①≈20 ;②≈0.3;
③≈500;④≈96.
解:这些结果都不正确.
怎样估算一个无理数的范围
你能估算它们的大小吗 说出你的方法.
①;②;③; ④.
(①②误差小于0.1;③误差小于10;④误差小于1)
解:≈6.3 ;≈0.9;
≈310 ;≈9.
(同伴间进行交流,教师适时引导.在解决问题的同时引导学生对解决方法进行总结,和学生一起归纳出估算的方法.)
(2)尝试用计算器求上述各式的值,检验你估算的准确性.
例2:比较与的大小.
解:与的分母相同,只要比较他们的分子就可以了,因为>2,所以-1>1,>.
例3:给出新的问题情境——画能挂上去吗
生活表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,
(1)他的顶端最多能到达多高(保留到0.1)
(2)现在如果请一个同学利用这个梯子在墙高5.9米的地方张贴一幅宣传画,他能办到吗
三、交流反思
学方根与立方根之后安排本节内容,目的很明确,就是要让学生体会如何运用这些知识去解决实际问题,体会到数学的实用价值,并逐步在今后的学习中有意识地运用估算的方法解决生活中的问题,发展学生的估算意识和数感.
尝试使用计算器进行数据的开平方和开立方运算,熟悉计算器按键,通过具体操作,使学生熟悉利用计算器求平方根和立方根的技能,激发学生的学习兴趣.
四、检测反馈
1.估算下列数的大小:
(1)(误差小于0.1);(2)(误差小于1).
2.通过估算,比较下面各数的大小:
(1)与.(2)与3.85.
3.一个人一生平均要引用的液体总量大约为40立方米,如果用圆柱形的容器(底面直径等于高)来装这些液体,这个容器大概有多高(误差小于1米)
五、布置作业
P39习题2.2 16,17,18
六、板书设计
2.平方根与立方根(4)
情境引入 活动探究 例1 例2 例3 巩固练习
七、教学反思
本节课的教学中选取了“修建环保公园”的问题情境引入,与学生平时的生活密切联系,容易把学生的积极性调动起来.在探究估算方法的时候,教师要注重适时的引导,以免让学生无从下手.在教学中要多鼓励学生用自己的语言表达他们的想法,在估算的过程中多给予适当的引导和评价,让学生逐步把握估算的方法,找到解决问题的信心.作为教师,一定要尊重学生的个体差异,满足多样化的学习需要,鼓励探究方式、表达方式和解题方法的多样化.
在教学过程中一定要让学生体会估算的实用价值,了解到“数学既来源与生活,又回归到生活为生活服务”.
同课章节目录
