4. 1 函数 教案 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4. 1 函数 教案 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:46:03 | ||
图片预览

文档简介
第四章 一次函数
1 函数
【教学目标】
1.初步掌握函数概念,能判断两个变量间的关系是否可以看成函数.
2.根据两个变量之间的关系式,给定其中一个量,相应的会求出另一个量的值.
3.了解函数的三种表示方法.
4.通过函数概念的学习,初步形成学生利用函数观点认识现实世界的意识和能力.
【重点难点】
重点:1.初步掌握函数概念,能判断两个变量间的关系是否可以看成函数.
2.根据两个变量之间的关系,给定其中一个量,相应的会求出另一个量的值.
难点:能判断两个变量间的关系是否可以看成函数.
【教学过程】
一、创设情境
问题1 你去过游乐园吗 你坐过摩天轮吗 你能描述一下坐摩天轮的感觉吗
当人坐在摩天轮上时,人的高度随时间在变化.
那么变化有规律吗
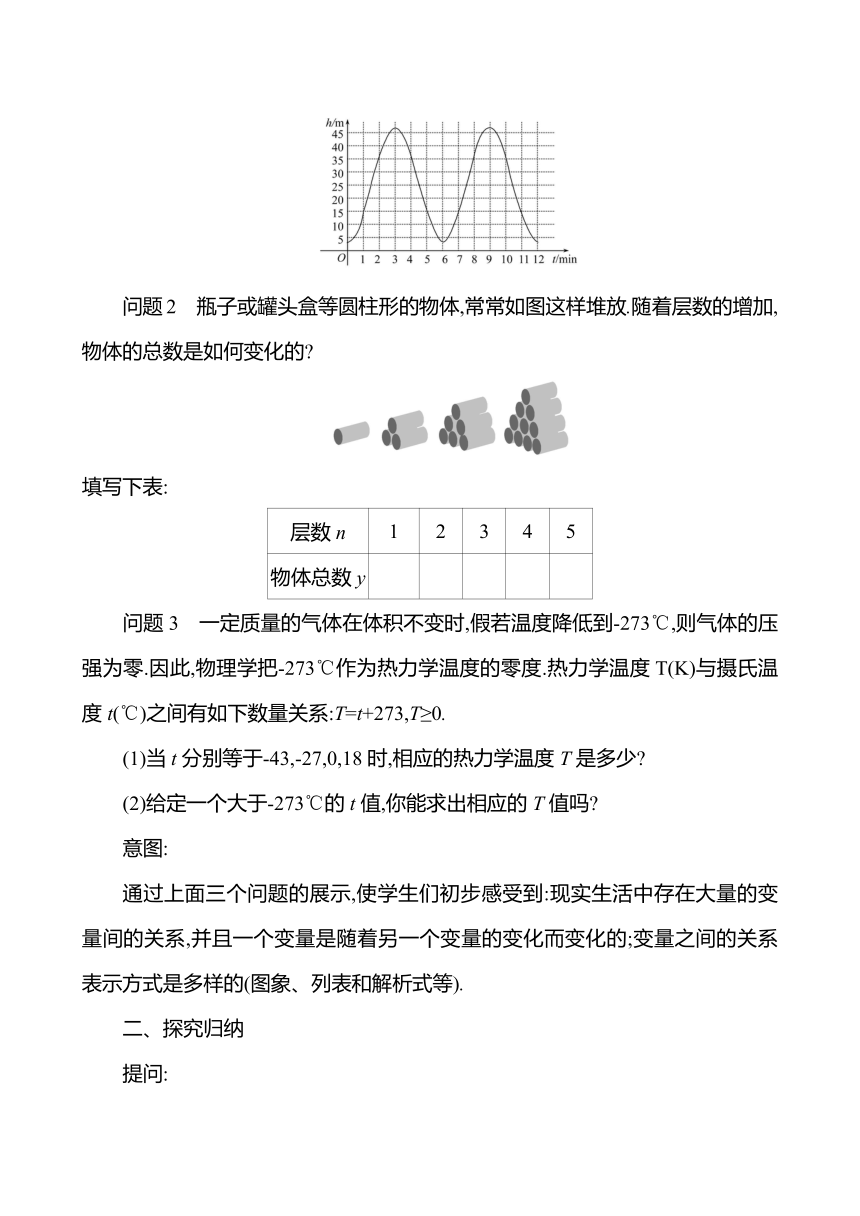
摩天轮上一点的高度h与旋转时间t之间有一定的关系,下图就反映了时间t(min)与摩天轮上一点的高度h(m)之间的关系.你能从图中观察出,有几个变化的量吗 当t分别取3,6,10时,相应的h是多少 给定一个t值,你都能找到相应的h值吗
问题2 瓶子或罐头盒等圆柱形的物体,常常如图这样堆放.随着层数的增加,物体的总数是如何变化的
填写下表:
层数n 1 2 3 4 5
物体总数y
问题3 一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少
(2)给定一个大于-273℃的t值,你能求出相应的T值吗
意图:
通过上面三个问题的展示,使学生们初步感受到:现实生活中存在大量的变量间的关系,并且一个变量是随着另一个变量的变化而变化的;变量之间的关系表示方式是多样的(图象、列表和解析式等).
二、探究归纳
提问:
1.引导学生思考以上三个问题的共同点,进而揭示出函数的概念:
(此过程让学生分组进行交流,协作完成)
在上面的问题中,都有两个变量,给定其中一个变量(自变量)的值,相应的就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
2.点明函数概念中的两个关键词:两个变量,一个x值确定一个y值,它们是判断函数关系的关键.
3.再通过对上面三个情境的比较,引导学生思考三个情境呈现形式的不同(依次以图象、表格、代数表达式的形式反映两个变量之间的关系),得出函数常用的三种表示方法:
(1)图象法; (2)列表法;
(3)解析法.
三、交流反思
1.本节课用到的基本思想是:通过观察、分析、对比、归纳等过程获取数学知识.
2.通过本节课,初步掌握函数的概念,并能判断两个变量之间的关系是否是函数的关系;并能由给定的自变量的值,相应的求出函数的值.
四、检测反馈
1.下列变量之间的关系不是函数关系的是 ( )
A.长方形的宽一定,其长与面积
B.正方形的边长与周长
C.长方形的周长与面积
D.球的体积与球的半径
2.用每片长6 cm的纸条,重叠1 cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸片的张数x之间的函数关系式是 ( )
A.y=6x+1 B.y=4x+1
C.y=4x+2 D.y=5x+1
五、布置作业
P77随堂练习
六、板书设计
4.1 函数 1.函数的概念 做一做: (1) (2) 2.函数的表示方法: (1) (3) (2) (3) (4)
七、教学反思
函数是研究现实世界变化规律的一个重要模型,对函数的学习一直以来都是中学阶段的一个重要的内容.函数的概念是学习后续“函数知识”的最重要的基础内容,而函数的概念又是比较抽象的,对它的理解一直是一个教学难点,学生对这些问题的探索以及研究思路都是比较陌生的,因此,在教学过程中,注意通过对以前学过的“变量之间的关系”的回顾与思考,力求提供生动有趣的问题情境,激发学生的学习兴趣;并通过层层深入的问题设计,引导学生进行观察、操作、交流、归纳等数学活动,在活动中归纳、概括出函数的概念;并通过师生交流、生生交流、辨析识别等加深学生对函数概念的理解.
1 函数
【教学目标】
1.初步掌握函数概念,能判断两个变量间的关系是否可以看成函数.
2.根据两个变量之间的关系式,给定其中一个量,相应的会求出另一个量的值.
3.了解函数的三种表示方法.
4.通过函数概念的学习,初步形成学生利用函数观点认识现实世界的意识和能力.
【重点难点】
重点:1.初步掌握函数概念,能判断两个变量间的关系是否可以看成函数.
2.根据两个变量之间的关系,给定其中一个量,相应的会求出另一个量的值.
难点:能判断两个变量间的关系是否可以看成函数.
【教学过程】
一、创设情境
问题1 你去过游乐园吗 你坐过摩天轮吗 你能描述一下坐摩天轮的感觉吗
当人坐在摩天轮上时,人的高度随时间在变化.
那么变化有规律吗
摩天轮上一点的高度h与旋转时间t之间有一定的关系,下图就反映了时间t(min)与摩天轮上一点的高度h(m)之间的关系.你能从图中观察出,有几个变化的量吗 当t分别取3,6,10时,相应的h是多少 给定一个t值,你都能找到相应的h值吗
问题2 瓶子或罐头盒等圆柱形的物体,常常如图这样堆放.随着层数的增加,物体的总数是如何变化的
填写下表:
层数n 1 2 3 4 5
物体总数y
问题3 一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少
(2)给定一个大于-273℃的t值,你能求出相应的T值吗
意图:
通过上面三个问题的展示,使学生们初步感受到:现实生活中存在大量的变量间的关系,并且一个变量是随着另一个变量的变化而变化的;变量之间的关系表示方式是多样的(图象、列表和解析式等).
二、探究归纳
提问:
1.引导学生思考以上三个问题的共同点,进而揭示出函数的概念:
(此过程让学生分组进行交流,协作完成)
在上面的问题中,都有两个变量,给定其中一个变量(自变量)的值,相应的就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
2.点明函数概念中的两个关键词:两个变量,一个x值确定一个y值,它们是判断函数关系的关键.
3.再通过对上面三个情境的比较,引导学生思考三个情境呈现形式的不同(依次以图象、表格、代数表达式的形式反映两个变量之间的关系),得出函数常用的三种表示方法:
(1)图象法; (2)列表法;
(3)解析法.
三、交流反思
1.本节课用到的基本思想是:通过观察、分析、对比、归纳等过程获取数学知识.
2.通过本节课,初步掌握函数的概念,并能判断两个变量之间的关系是否是函数的关系;并能由给定的自变量的值,相应的求出函数的值.
四、检测反馈
1.下列变量之间的关系不是函数关系的是 ( )
A.长方形的宽一定,其长与面积
B.正方形的边长与周长
C.长方形的周长与面积
D.球的体积与球的半径
2.用每片长6 cm的纸条,重叠1 cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸片的张数x之间的函数关系式是 ( )
A.y=6x+1 B.y=4x+1
C.y=4x+2 D.y=5x+1
五、布置作业
P77随堂练习
六、板书设计
4.1 函数 1.函数的概念 做一做: (1) (2) 2.函数的表示方法: (1) (3) (2) (3) (4)
七、教学反思
函数是研究现实世界变化规律的一个重要模型,对函数的学习一直以来都是中学阶段的一个重要的内容.函数的概念是学习后续“函数知识”的最重要的基础内容,而函数的概念又是比较抽象的,对它的理解一直是一个教学难点,学生对这些问题的探索以及研究思路都是比较陌生的,因此,在教学过程中,注意通过对以前学过的“变量之间的关系”的回顾与思考,力求提供生动有趣的问题情境,激发学生的学习兴趣;并通过层层深入的问题设计,引导学生进行观察、操作、交流、归纳等数学活动,在活动中归纳、概括出函数的概念;并通过师生交流、生生交流、辨析识别等加深学生对函数概念的理解.
同课章节目录
