2024新人教版八年级上数学 15.1.1 轴对称及其性质(第2课时) 课件(共28张PPT)
文档属性
| 名称 | 2024新人教版八年级上数学 15.1.1 轴对称及其性质(第2课时) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 11:38:49 | ||
图片预览




文档简介
(共28张PPT)
人教版(2024)
八年级上册
15.1 图形的轴对称
15.1.1 轴对称及其性质(第2课时)
第十五章 · 轴对称
轴对称及其性质
知识目标
1.准确理解“线段垂直平分线”的定义,明确其双重属性——几何位置与度量关系。
2.掌握图形轴对称的核心特征,对应点连线被对称轴垂直平分、折叠后完全重合,建立与线段垂直平分线的内在联系。
能力目标
2.基于定义推导垂直平分线上任意一点到线段两端距离相等的性质,培养演绎思维能力。
3.通过动态演示,直观感知轴对称图形沿垂直平分线折叠后的重合现象,提升空间转换能力。
素质目标
1严谨对待作图误差,养成反复校验的习惯;通过探究活动培养质疑精神与实证意识。
2.欣赏自然界与艺术作品中的轴对称之美,激发用数学眼光观察世界的情趣。
教学难点
教学重点
理解线段垂直平分线的意义和线段的轴对称性并用其作图.
理解线段垂直平分线的意义和线段的轴对称性并用其作图.
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
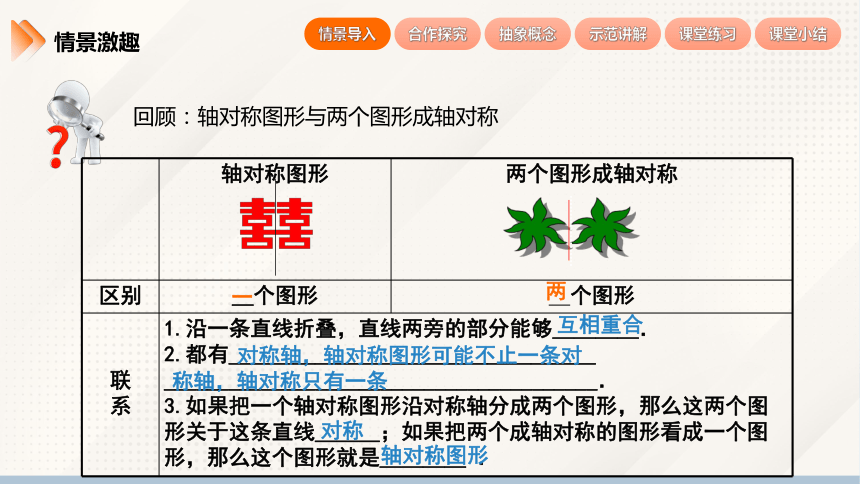
回顾:轴对称图形与两个图形成轴对称
轴对称图形 两个图形成轴对称
区别 _个图形 _个图形
联 系 1.沿一条直线折叠,直线两旁的部分能够____. 2.都有_________________________________________________________. 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____ . 一
两
互相重合
对称轴,轴对称图形可能不止一条对
称轴,轴对称只有一条
对称
轴对称图形
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
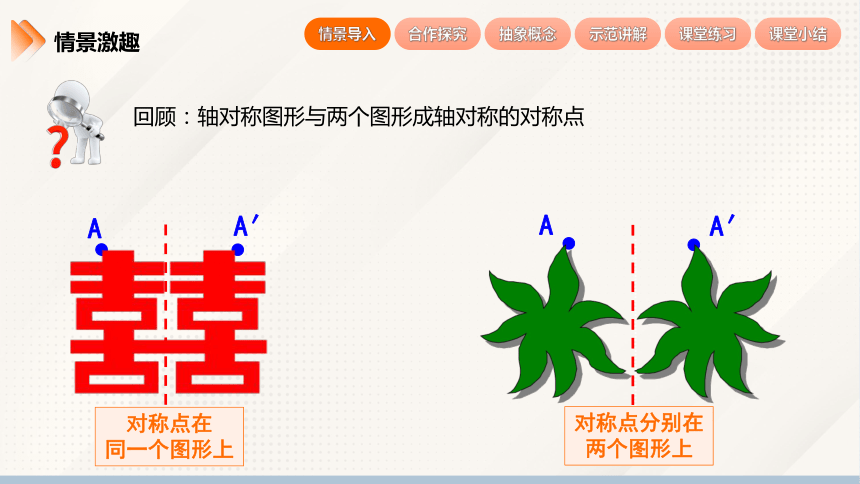
回顾:轴对称图形与两个图形成轴对称的对称点
A
A′
A
A′
对称点在
同一个图形上
对称点分别在两个图形上
分析问题,寻找对应
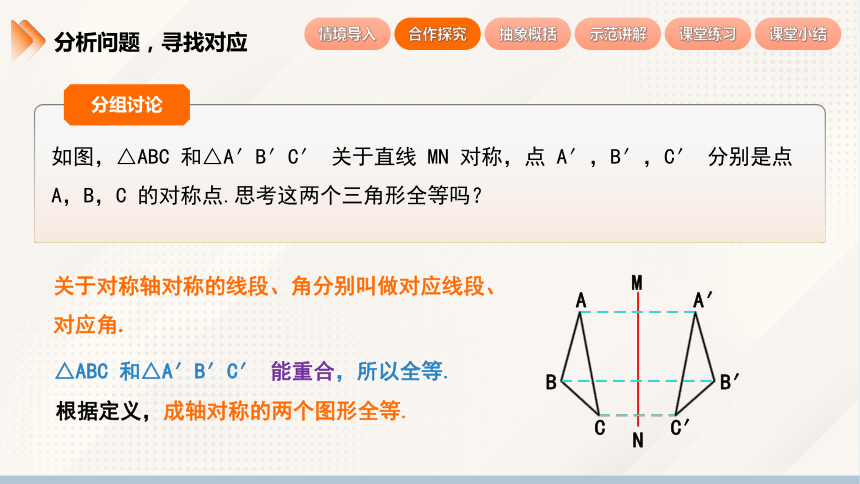
如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点.思考这两个三角形全等吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
M
N
A′
B′
C′
关于对称轴对称的线段、角分别叫做对应线段、对应角.
△ABC 和△A′B′C′ 能重合,所以全等.
根据定义,成轴对称的两个图形全等.
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
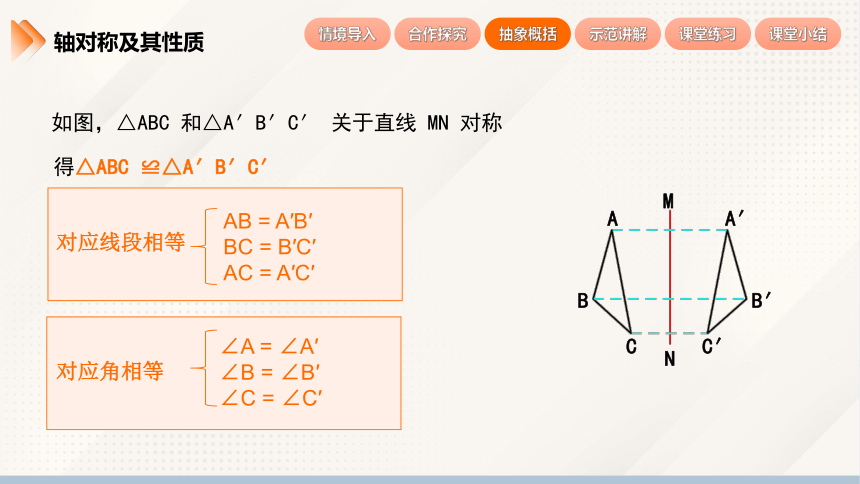
对应线段相等
对应角相等
如图,△ABC 和△A′B′C′ 关于直线 MN 对称
A
B
C
M
N
A′
B′
C′
得△ABC ≌△A′B′C′
AB = A′B′
BC = B′C′
AC = A′C′
∠A = ∠A′
∠B = ∠B′
∠C = ∠C′
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
任务:折纸
准备不同形状的彩色卡纸,卡纸上有一条任意方向线段AB.
A
B
折一折,通过折叠使A、B两点完全重合
分析问题,寻找对应
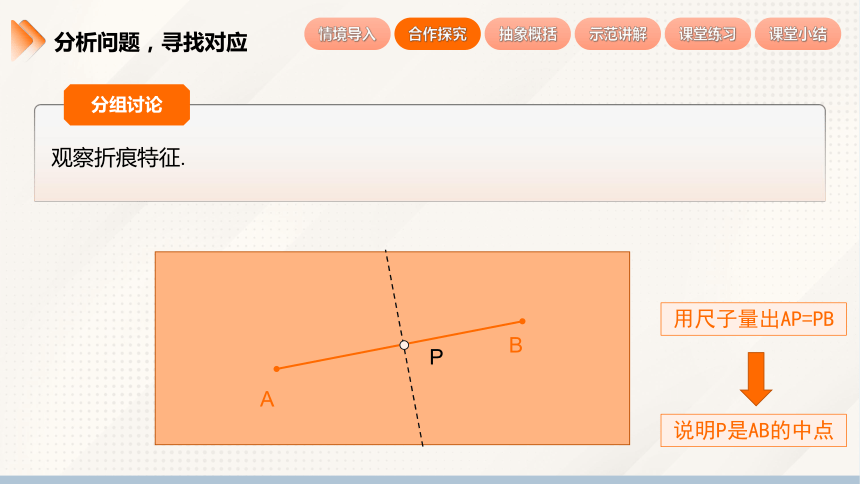
观察折痕特征.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
P
用尺子量出AP=PB
说明P是AB的中点
分析问题,寻找对应
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A′
B′
C′
N
M
结论:AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
分析问题,寻找对应
如果将其中的“三角形”改为“四边形”“五边形”……其他条件不变,上述结论还成立吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
C
B
A′
C′
B′
M
N
D
D′
A
C
B
A′
C′
B′
M
N
D
D′
E
E′
分析问题,寻找对应
轴对称图形中也有同样的性质吗?
如图,画出正五边形的其中一条对称轴l,标出A与它的对称点A′、B与它的对称点B′.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
A′
B′
l
将这个五边形沿 l 分成两个图形,转化成成轴对称的两个图形
由轴对称的性质可知:
直线 l 经过AA′,BB′ 的______,且 l ____ AA′,l ____ BB′.
中点
⊥
⊥
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
轴对称的性质
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
垂直平分线
经过线段中点并且垂直于这条线段的直线,叫作这条线段的垂直平分线.
A
B
l
直线 l 是线段 AB 的垂直平分线
无论是成轴对称的两个图形,还是轴对称图形,其对称轴都是其任意一对对应点所连线段的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN与点O,则下列说法不一定正确的是( ).
C
A'
A
B
B'
C'
O
N
M
A.AC=A'C' B.BO=B'O C.AA'⊥MN D.AB∥B'C'
D
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
如图,△ABC和△A′B′C′,关于直线l 对称,且∠B =80°,A′B′ =6 cm,求∠B′的度数和AB的长.
分析: △ABC 和 △A′B′C′ 关于直线l对称, ∠B 和∠B'是对应角,AB 和A′B′ 是对应边.
因此,∠B =∠B′=80°,AB= A′B′ =6 cm.
解:∵ 和 关于直线l对称,
∴ ∠B =∠B′, = .
∵ ∠B =80°, =6 cm
∴ ∠B′=80°,=6 cm .
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例3
如图,线段 AB 与 A′B′ 关于直线 l 对称,AA′ 交直线 l 于点 O,连接 BO,B′O.
(1) 图中相等的线段有:
_______________________________,
线段 AA′ 的垂直平分线是 ______;
(2) △OAB 和△OA′B′ 关于直线
l ________,△OAB _____△OA′B′,
∠ABO = _______,∠A′OB′ =________.
A
B
A′
B′
l
O
AB = A'B',AO = A'O,BO = B'O
直线 l
对称
≌
∠A'B'O
∠AOB
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
如图,△ABC 和△A′B′C′ 关于直线 l 对称,∠B = 90°,A′B′= 6. 求∠B′的度数和AB的长 .
解:∵△ABC和△A'B'C' 关于直线 l 对称,
∴△ABC≌△A'B'C'.
∴∠B' =∠B = 90°,
AB = A'B' = 6.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,△ABC 与△A'B'C' 关于直线 MN 对称,BB' 交 MN 于点 O,∠BAC = 30°,∠ABC = 130°,A'C' = 6.
(1)∠A'C'B' = _______,
AC = _______;
(2)若 BB' = 4,则 OB' = ___;
20°
O
A
C
B
A′
C′
B′
M
N
6
2
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB = AC,DB = DC,点 E 在 AD 上 . 求证 EB = EC.
证明:如图,连接 BC.
∵AB = AC,
∴点 A 在线段 BC 的垂直平分线上.
∵DB = DC,
∴点 D 也在线段 BC 的垂直平分线上.
∴直线 AD 是线段 BC 的垂直平分线.
又点 E 在 AD 上,∴EB = EC.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.如图,△ABC 与△A'B'C' 关于关于直线MN对称,BB’交MN于点O,下列结论:①AB=A’B’;②OB=OB’;③AA’//BB’中,正确的有( )
A.3个 B.2个 C.1个 D.0个
【答案】A
【分析】根据轴对称的性质对各选项分析判断后利用排除法求解.
【详解】∵△ABC 与△A'B'C' 关于关于直线MN对称
∴OB=OB’,△ABC≌△A'B'C', AA’//BB’
∴AB=A’B’
所以正确的一共有3个,
故选:A.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·山东青岛·中考真题)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC 关于y轴的对称图形绕原点O旋转,得到△A1B1C1 ,则点A的对应点A1的坐标是( )
A.(-1,-2) B.(1,2)
C.(2,1) D.(-2,-1)
D
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·河北·中考真题)如图,AD与BC交于点O,△ABO 和△CDO 关于直线对称,点A,B的对称点分别是点C,D.下列不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO≌△CDO D.AC//BD
【答案】B
【详解】∵△ABO 与△CDO 关于关于直线PQ对称
∴△ABO≌△CDO,AC⊥PQ
∴AC//BD
所以B、C、D不满足题意.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
推导“线段垂直平分线”的定义
利用轴对称的性质完成证明题
理解“线段垂直平分线”的定义
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
轴对称的性质
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
垂直平分线
经过线段中点并且垂直于这条线段的直线,叫作这条线段的垂直平分线.
A
B
l
直线 l 是线段 AB 的垂直平分线
无论是成轴对称的两个图形,还是轴对称图形,其对称轴都是其任意一对对应点所连线段的垂直平分线.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:3题.
B层:P69习题 15.1:11题.
下 课
人教版(2024)
八年级上册
15.1 图形的轴对称
15.1.1 轴对称及其性质(第2课时)
第十五章 · 轴对称
轴对称及其性质
知识目标
1.准确理解“线段垂直平分线”的定义,明确其双重属性——几何位置与度量关系。
2.掌握图形轴对称的核心特征,对应点连线被对称轴垂直平分、折叠后完全重合,建立与线段垂直平分线的内在联系。
能力目标
2.基于定义推导垂直平分线上任意一点到线段两端距离相等的性质,培养演绎思维能力。
3.通过动态演示,直观感知轴对称图形沿垂直平分线折叠后的重合现象,提升空间转换能力。
素质目标
1严谨对待作图误差,养成反复校验的习惯;通过探究活动培养质疑精神与实证意识。
2.欣赏自然界与艺术作品中的轴对称之美,激发用数学眼光观察世界的情趣。
教学难点
教学重点
理解线段垂直平分线的意义和线段的轴对称性并用其作图.
理解线段垂直平分线的意义和线段的轴对称性并用其作图.
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:轴对称图形与两个图形成轴对称
轴对称图形 两个图形成轴对称
区别 _个图形 _个图形
联 系 1.沿一条直线折叠,直线两旁的部分能够____. 2.都有_________________________________________________________. 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____ . 一
两
互相重合
对称轴,轴对称图形可能不止一条对
称轴,轴对称只有一条
对称
轴对称图形
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:轴对称图形与两个图形成轴对称的对称点
A
A′
A
A′
对称点在
同一个图形上
对称点分别在两个图形上
分析问题,寻找对应
如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点.思考这两个三角形全等吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
M
N
A′
B′
C′
关于对称轴对称的线段、角分别叫做对应线段、对应角.
△ABC 和△A′B′C′ 能重合,所以全等.
根据定义,成轴对称的两个图形全等.
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
对应线段相等
对应角相等
如图,△ABC 和△A′B′C′ 关于直线 MN 对称
A
B
C
M
N
A′
B′
C′
得△ABC ≌△A′B′C′
AB = A′B′
BC = B′C′
AC = A′C′
∠A = ∠A′
∠B = ∠B′
∠C = ∠C′
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
任务:折纸
准备不同形状的彩色卡纸,卡纸上有一条任意方向线段AB.
A
B
折一折,通过折叠使A、B两点完全重合
分析问题,寻找对应
观察折痕特征.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
P
用尺子量出AP=PB
说明P是AB的中点
分析问题,寻找对应
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A′
B′
C′
N
M
结论:AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
分析问题,寻找对应
如果将其中的“三角形”改为“四边形”“五边形”……其他条件不变,上述结论还成立吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
C
B
A′
C′
B′
M
N
D
D′
A
C
B
A′
C′
B′
M
N
D
D′
E
E′
分析问题,寻找对应
轴对称图形中也有同样的性质吗?
如图,画出正五边形的其中一条对称轴l,标出A与它的对称点A′、B与它的对称点B′.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
A′
B′
l
将这个五边形沿 l 分成两个图形,转化成成轴对称的两个图形
由轴对称的性质可知:
直线 l 经过AA′,BB′ 的______,且 l ____ AA′,l ____ BB′.
中点
⊥
⊥
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
轴对称的性质
轴对称及其性质
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
垂直平分线
经过线段中点并且垂直于这条线段的直线,叫作这条线段的垂直平分线.
A
B
l
直线 l 是线段 AB 的垂直平分线
无论是成轴对称的两个图形,还是轴对称图形,其对称轴都是其任意一对对应点所连线段的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN与点O,则下列说法不一定正确的是( ).
C
A'
A
B
B'
C'
O
N
M
A.AC=A'C' B.BO=B'O C.AA'⊥MN D.AB∥B'C'
D
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
如图,△ABC和△A′B′C′,关于直线l 对称,且∠B =80°,A′B′ =6 cm,求∠B′的度数和AB的长.
分析: △ABC 和 △A′B′C′ 关于直线l对称, ∠B 和∠B'是对应角,AB 和A′B′ 是对应边.
因此,∠B =∠B′=80°,AB= A′B′ =6 cm.
解:∵ 和 关于直线l对称,
∴ ∠B =∠B′, = .
∵ ∠B =80°, =6 cm
∴ ∠B′=80°,=6 cm .
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例3
如图,线段 AB 与 A′B′ 关于直线 l 对称,AA′ 交直线 l 于点 O,连接 BO,B′O.
(1) 图中相等的线段有:
_______________________________,
线段 AA′ 的垂直平分线是 ______;
(2) △OAB 和△OA′B′ 关于直线
l ________,△OAB _____△OA′B′,
∠ABO = _______,∠A′OB′ =________.
A
B
A′
B′
l
O
AB = A'B',AO = A'O,BO = B'O
直线 l
对称
≌
∠A'B'O
∠AOB
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
如图,△ABC 和△A′B′C′ 关于直线 l 对称,∠B = 90°,A′B′= 6. 求∠B′的度数和AB的长 .
解:∵△ABC和△A'B'C' 关于直线 l 对称,
∴△ABC≌△A'B'C'.
∴∠B' =∠B = 90°,
AB = A'B' = 6.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,△ABC 与△A'B'C' 关于直线 MN 对称,BB' 交 MN 于点 O,∠BAC = 30°,∠ABC = 130°,A'C' = 6.
(1)∠A'C'B' = _______,
AC = _______;
(2)若 BB' = 4,则 OB' = ___;
20°
O
A
C
B
A′
C′
B′
M
N
6
2
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB = AC,DB = DC,点 E 在 AD 上 . 求证 EB = EC.
证明:如图,连接 BC.
∵AB = AC,
∴点 A 在线段 BC 的垂直平分线上.
∵DB = DC,
∴点 D 也在线段 BC 的垂直平分线上.
∴直线 AD 是线段 BC 的垂直平分线.
又点 E 在 AD 上,∴EB = EC.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.如图,△ABC 与△A'B'C' 关于关于直线MN对称,BB’交MN于点O,下列结论:①AB=A’B’;②OB=OB’;③AA’//BB’中,正确的有( )
A.3个 B.2个 C.1个 D.0个
【答案】A
【分析】根据轴对称的性质对各选项分析判断后利用排除法求解.
【详解】∵△ABC 与△A'B'C' 关于关于直线MN对称
∴OB=OB’,△ABC≌△A'B'C', AA’//BB’
∴AB=A’B’
所以正确的一共有3个,
故选:A.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·山东青岛·中考真题)如图,在平面直角坐标系中,点A,B,C都在格点上,将△ABC 关于y轴的对称图形绕原点O旋转,得到△A1B1C1 ,则点A的对应点A1的坐标是( )
A.(-1,-2) B.(1,2)
C.(2,1) D.(-2,-1)
D
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·河北·中考真题)如图,AD与BC交于点O,△ABO 和△CDO 关于直线对称,点A,B的对称点分别是点C,D.下列不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO≌△CDO D.AC//BD
【答案】B
【详解】∵△ABO 与△CDO 关于关于直线PQ对称
∴△ABO≌△CDO,AC⊥PQ
∴AC//BD
所以B、C、D不满足题意.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
推导“线段垂直平分线”的定义
利用轴对称的性质完成证明题
理解“线段垂直平分线”的定义
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
轴对称的性质
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
垂直平分线
经过线段中点并且垂直于这条线段的直线,叫作这条线段的垂直平分线.
A
B
l
直线 l 是线段 AB 的垂直平分线
无论是成轴对称的两个图形,还是轴对称图形,其对称轴都是其任意一对对应点所连线段的垂直平分线.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:3题.
B层:P69习题 15.1:11题.
下 课
同课章节目录
