15.1.2 线段的垂直平分 第1课时 线段的垂直平分线的性质和判定 课件(共35张PPT)
文档属性
| 名称 | 15.1.2 线段的垂直平分 第1课时 线段的垂直平分线的性质和判定 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:57:39 | ||
图片预览





文档简介
(共35张PPT)
人教版(2024)
八年级上册
15.1.2 线段的垂直平分
第1课时 线段的垂直平分
线的性质和判定
第十五章 · 轴对称
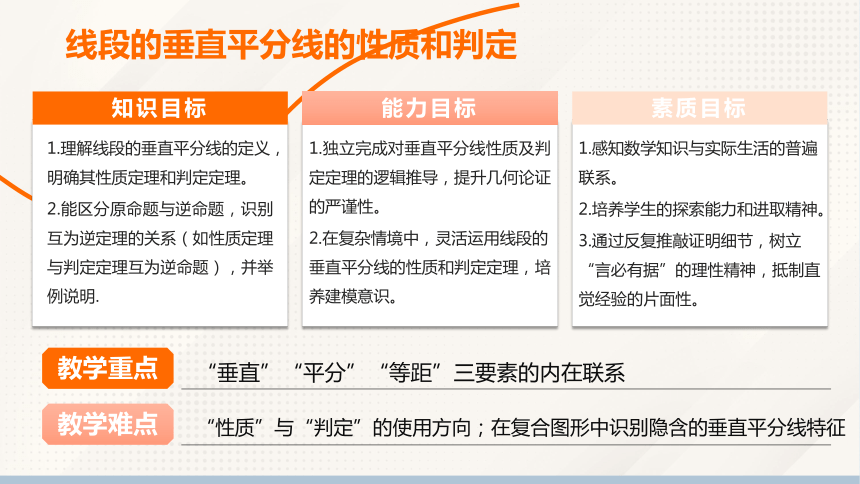
线段的垂直平分线的性质和判定
知识目标
1.理解线段的垂直平分线的定义,明确其性质定理和判定定理。
2.能区分原命题与逆命题,识别互为逆定理的关系(如性质定理与判定定理互为逆命题),并举例说明.
能力目标
1.独立完成对垂直平分线性质及判定定理的逻辑推导,提升几何论证的严谨性。
2.在复杂情境中,灵活运用线段的垂直平分线的性质和判定定理,培养建模意识。
素质目标
1.感知数学知识与实际生活的普遍联系。
2.培养学生的探索能力和进取精神。
3.通过反复推敲证明细节,树立“言必有据”的理性精神,抵制直觉经验的片面性。
教学难点
教学重点
“垂直”“平分”“等距”三要素的内在联系
“性质”与“判定”的使用方向;在复合图形中识别隐含的垂直平分线特征
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:线段的垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(简称中垂线).
A
B
l
C
符号语言:
点C是线段AB的中点,且l⊥AB于C,
直线l是线段AB的垂直平分线.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
思考:线段是轴对称图形吗?
请画一条线段 AB,你能找到线段的对称轴吗?
A
B
思考:线段的对称轴和它有怎样的关系?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
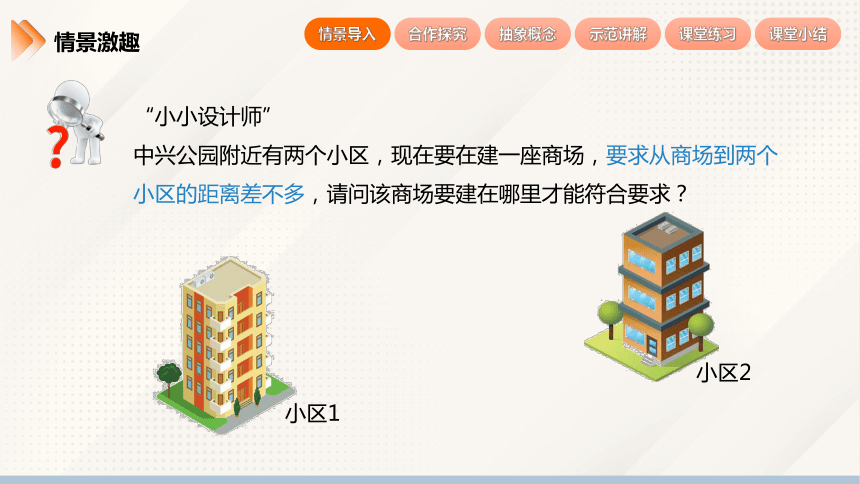
“小小设计师”
中兴公园附近有两个小区,现在要在建一座商场,要求从商场到两个小区的距离差不多,请问该商场要建在哪里才能符合要求?
小区1
小区2
分析问题,寻找对应
如图,直线 l 垂直平分线段 AB,点 P1,P2,P3,…在 l 上,分别比较点 P1,P2,P3,… 与点 A 的距离和这些点与点 B 的距离,你有什么发现?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
l
P1
P2
P3
我量一量,发现P1A = P1B,P2A = P2B,P3A = P3B...
沿l对折, P1A 与 P1B,P2A 与 P2B,P3A 与 P3B 都重合,说明P1A = P1B,P2A = P2B,P3A = P3B
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
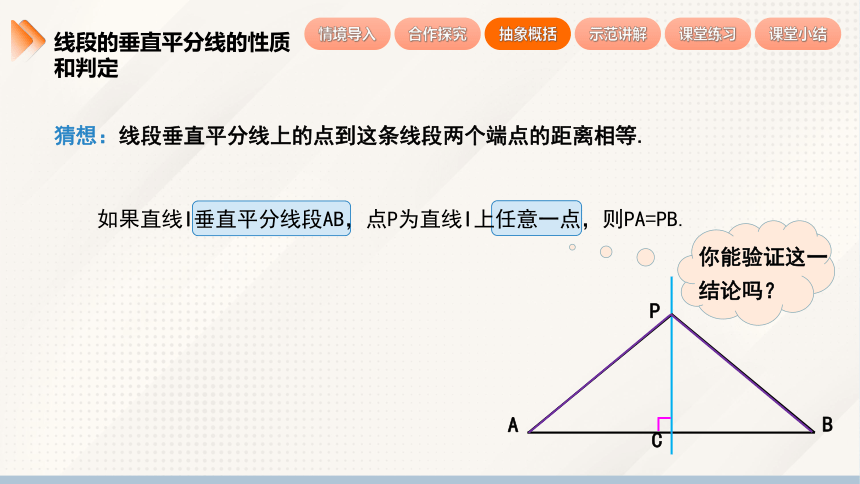
猜想:线段垂直平分线上的点到这条线段两个端点的距离相等.
如果直线l垂直平分线段AB,点P为直线l上任意一点,则PA=PB.
A
B
l
P
C
你能验证这一结论吗?
分析问题,寻找对应
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
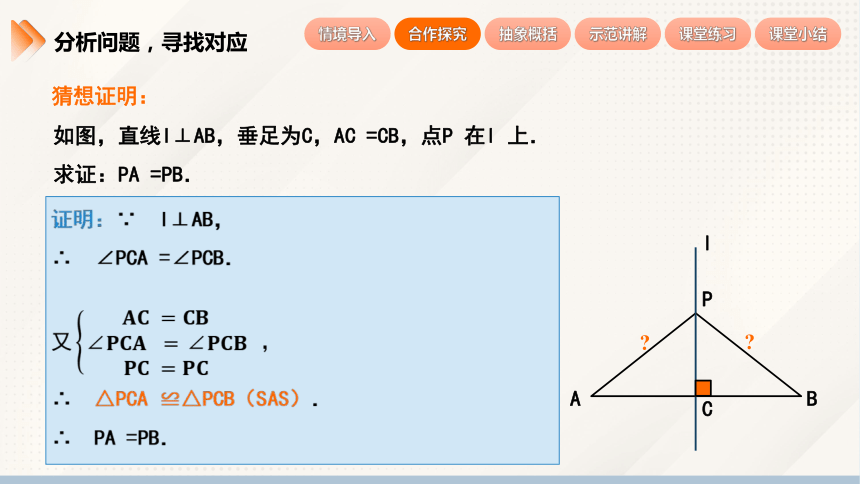
如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
猜想证明:
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
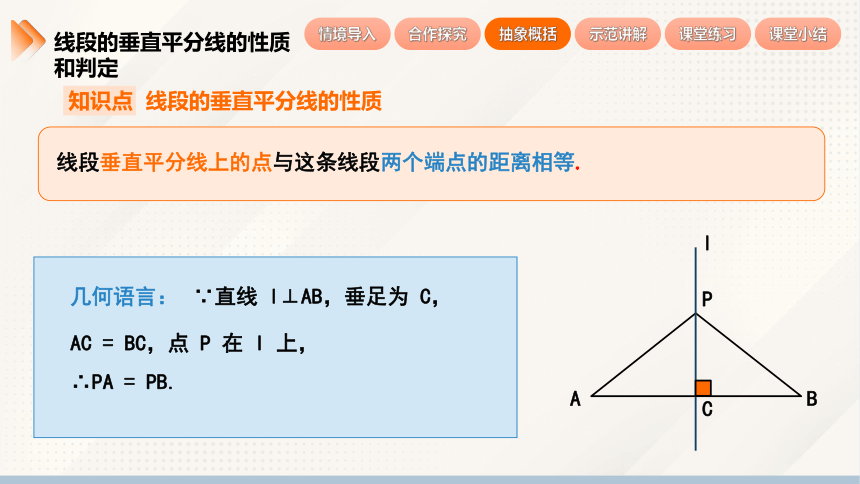
知识点 线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
分析问题,寻找对应
把上面线段的垂直平分线的性质的题设和结论反过来,得到的命题还成立吗?即如果 PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
猜想:点 P 在线段 AB 的垂直平分线上
A
B
P
已知:如图,在△ABP 中 PA = PB.
求证:点 P 在线段 AB 的垂直平分线上.
分析问题,寻找对应
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
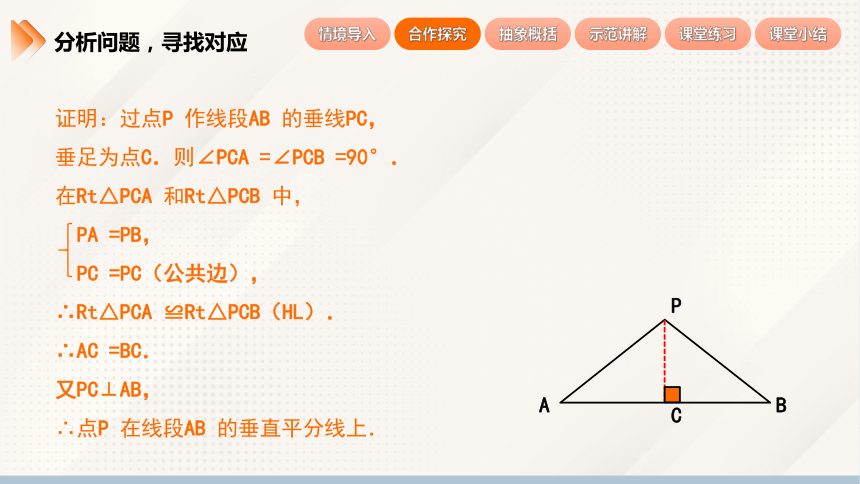
证明:过点P 作线段AB 的垂线PC,
垂足为点C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,
PC =PC(公共边),
∴Rt△PCA ≌Rt△PCB(HL).
∴AC =BC.
又PC⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
C
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA = PB,
∴点 P 在 AB 的垂直平分线上..
几何语言:
P
A
B
l
C
线段的垂直平分线可以看成与这条线
段两个端点距离相等的所有点的集合.
作用:判断一个点是否在线段的垂直平分线上.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
“小小设计师”
中兴公园附近有两个小区,现在要在建一座商场,要求从商场到两个小区的距离差不多,请问该商场要建在哪里才能符合要求?
小区1
小区2
商场应该建在两个小区连线的垂直平分线上才符合要求
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 对比角的平分线与线段的垂直平分线
名称 角平分线 线段垂直平分线
图示
性质
判定
C
A
B
O
D
E
P
A
B
P
C
角平分线上的点到角两边的距离相等
线段垂直平分线上的点与这条线段两个端点的距离相等
角的内部到角两边距离相等的点在角的平分线上
与线段两个端点距离相等的点在这条线段的垂直平分线上
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
分组讨论
线段垂直平分线上的点与这条线段两个端点的距离相等
与线段两个端点距离相等的点在这条线段的垂直平分线上
两个命题的题设、结论正好相反.
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
两个命题的题设、结论正好相反.
我们把具有这种关系的两个命题叫作互逆命题. 如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
线段的垂直平分线的性质与判定
“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”
一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
都成立
成立
不成立
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
线段的垂直平分线的性质与判定
“两直线平行,内错角相等”与“内错角相等,两直线平行”
角的平分线的性质与判定
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
解
已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE(角平分线上的点到角的两边的距离相等).
∴ OE是CD的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(1)写出命题“全等三角形的面积相等"的逆命题 .
(2)直角三角形的两个锐角互余的逆命题为 .
(3)命题"正方形是轴对称图形”的逆命题是 .
例2
交换原命题的题设和结论
面积相等的三角形全等
有两个角互余的三角形是直角三角形
轴对称图形是正方形
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,AB=8,则ΔABE的周长为 .
例3
解
[答案]18
[详解]解:∵DE是BC的垂直平分线,交AC于点E,
∴EB=EC,
∵点F是线段AC的中点, AC=2CF,
∵△ABE的周长是AB+BE+AE=AB+EC+AE
=AB+AC,CF=5,AB=8,
∴AB+BE+AE=AB+AC=8+2x5=18.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,AD⊥BC,BD = DC,点 C 在 AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
A
B
E
D
C
解:AB = AC = CE,AB + BD = DE.
理由:
∵AD⊥BC,BD = DC,
∴AD 是 BC 的垂直平分线.
∴AB = AC.
又点 C 在 AE 的垂直平分线上,
∴AC = CE.
∴AB = AC = CE.
又 BD = DC,
∴AB + BD = CE + DC,即 AB + BD = DE.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图, AB=AC, MB=MC. 直线AM 是线段BC 的垂直平分线吗 为什么
解:∵AB=AC,MB=MC,
∴直线AM是线段BC的垂直平分线,(到线段两端距离相等的点在这条线段的垂直平分线上)
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)两直线平行,同位角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
解:(1)同位角相等,两直线平行,为真命题
(2)如果两个实数的绝对值相等,那么它们也相等,为假命题
(3)如果两个三角形的对应角相等,那么它们为全等三角形,为假命题
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4. 如图,P 是 △ABC 内一点,若 PB = PC,则点 P 在( )
A.∠ABC 的平分线上
B.∠ACB 的平分线上
C.边 AB 的垂直平分线上
D.边 BC 的垂直平分线上
D
5.如图,在△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是 ( )
A.8 B.9 C.10 D.11
C
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6. 如图,公园里有一块三角形草坪(△ABC),现准备在该三角形草坪内种一棵树,使得该树到△ABC 三个顶点的距离相等,则该树应种在( )
A.三条边的垂直平分线的交点处
B.三条角平分线的交点处
C.三条高的交点处
D.三条中线的交点处
A
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·江苏连云港·中考真题)如图,在△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,则△AEG的周长为( )
A.5 B.6 C.7 D.8
[答案]C
[分析]本题考查了线段垂直平分线的性质,由线段垂直平分线的性质可得AE=BE,AG=CG,再由三角形的周长公式计算即可得解,熟练掌握线段垂直平分线的性质是解此题的关键,
[详解]解:∵DE垂直平分AB,GF垂直平分AC,
∴AE=BE,AG=CG,
∴△AEG的周长为AE+AG+EG=BE+CG+EG=BC=7,
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2025·四川达州·中考真题)如图,在△ABC中,AB=AC-8,BC=5,线段AB的垂直平分线交AB于点E,交AC于点D,则△BDC的周长为( )
A.21 B.14 C.13 D.9
[答案]C
[分析]本题主要考查了线段垂直平分线的性质,根据线段垂直平分线的性质可得AD=BD,据此根据三角形周长计算公式求解即可.
[详解]解:.线段AB的垂直平分线交AB于点E,交AC于点D,
∴AD=BD,
∴△BDC的周长=BD+BC+CD=BC+CD+AD=BC+AC=8+5=13,
故选: C.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
垂直平分线性质及判定定理
完成对垂直平分线性质及判定定理的逻辑推导
能区分原命题与逆命题
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA = PB,
∴点 P 在 AB 的垂直平分线上..
几何语言:
P
A
B
l
C
线段的垂直平分线可以看成与这条线
段两个端点距离相等的所有点的集合.
作用:判断一个点是否在线段的垂直平分线上.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 对比角的平分线与线段的垂直平分线
名称 角平分线 线段垂直平分线
图示
性质
判定
C
A
B
O
D
E
P
A
B
P
C
角平分线上的点到角两边的距离相等
线段垂直平分线上的点与这条线段两个端点的距离相等
角的内部到角两边距离相等的点在角的平分线上
与线段两个端点距离相等的点在这条线段的垂直平分线上
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
两个命题的题设、结论正好相反.
我们把具有这种关系的两个命题叫作互逆命题. 如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:4、6题.
B层:P69习题 15.1:5题.
下 课
人教版(2024)
八年级上册
15.1.2 线段的垂直平分
第1课时 线段的垂直平分
线的性质和判定
第十五章 · 轴对称
线段的垂直平分线的性质和判定
知识目标
1.理解线段的垂直平分线的定义,明确其性质定理和判定定理。
2.能区分原命题与逆命题,识别互为逆定理的关系(如性质定理与判定定理互为逆命题),并举例说明.
能力目标
1.独立完成对垂直平分线性质及判定定理的逻辑推导,提升几何论证的严谨性。
2.在复杂情境中,灵活运用线段的垂直平分线的性质和判定定理,培养建模意识。
素质目标
1.感知数学知识与实际生活的普遍联系。
2.培养学生的探索能力和进取精神。
3.通过反复推敲证明细节,树立“言必有据”的理性精神,抵制直觉经验的片面性。
教学难点
教学重点
“垂直”“平分”“等距”三要素的内在联系
“性质”与“判定”的使用方向;在复合图形中识别隐含的垂直平分线特征
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:线段的垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(简称中垂线).
A
B
l
C
符号语言:
点C是线段AB的中点,且l⊥AB于C,
直线l是线段AB的垂直平分线.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
思考:线段是轴对称图形吗?
请画一条线段 AB,你能找到线段的对称轴吗?
A
B
思考:线段的对称轴和它有怎样的关系?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
“小小设计师”
中兴公园附近有两个小区,现在要在建一座商场,要求从商场到两个小区的距离差不多,请问该商场要建在哪里才能符合要求?
小区1
小区2
分析问题,寻找对应
如图,直线 l 垂直平分线段 AB,点 P1,P2,P3,…在 l 上,分别比较点 P1,P2,P3,… 与点 A 的距离和这些点与点 B 的距离,你有什么发现?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
l
P1
P2
P3
我量一量,发现P1A = P1B,P2A = P2B,P3A = P3B...
沿l对折, P1A 与 P1B,P2A 与 P2B,P3A 与 P3B 都重合,说明P1A = P1B,P2A = P2B,P3A = P3B
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
猜想:线段垂直平分线上的点到这条线段两个端点的距离相等.
如果直线l垂直平分线段AB,点P为直线l上任意一点,则PA=PB.
A
B
l
P
C
你能验证这一结论吗?
分析问题,寻找对应
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
猜想证明:
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
分析问题,寻找对应
把上面线段的垂直平分线的性质的题设和结论反过来,得到的命题还成立吗?即如果 PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
猜想:点 P 在线段 AB 的垂直平分线上
A
B
P
已知:如图,在△ABP 中 PA = PB.
求证:点 P 在线段 AB 的垂直平分线上.
分析问题,寻找对应
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
证明:过点P 作线段AB 的垂线PC,
垂足为点C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,
PC =PC(公共边),
∴Rt△PCA ≌Rt△PCB(HL).
∴AC =BC.
又PC⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
C
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA = PB,
∴点 P 在 AB 的垂直平分线上..
几何语言:
P
A
B
l
C
线段的垂直平分线可以看成与这条线
段两个端点距离相等的所有点的集合.
作用:判断一个点是否在线段的垂直平分线上.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
“小小设计师”
中兴公园附近有两个小区,现在要在建一座商场,要求从商场到两个小区的距离差不多,请问该商场要建在哪里才能符合要求?
小区1
小区2
商场应该建在两个小区连线的垂直平分线上才符合要求
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 对比角的平分线与线段的垂直平分线
名称 角平分线 线段垂直平分线
图示
性质
判定
C
A
B
O
D
E
P
A
B
P
C
角平分线上的点到角两边的距离相等
线段垂直平分线上的点与这条线段两个端点的距离相等
角的内部到角两边距离相等的点在角的平分线上
与线段两个端点距离相等的点在这条线段的垂直平分线上
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
分组讨论
线段垂直平分线上的点与这条线段两个端点的距离相等
与线段两个端点距离相等的点在这条线段的垂直平分线上
两个命题的题设、结论正好相反.
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
两个命题的题设、结论正好相反.
我们把具有这种关系的两个命题叫作互逆命题. 如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
线段的垂直平分线的性质与判定
“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”
一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
都成立
成立
不成立
线段的垂直平分线的性质和判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
线段的垂直平分线的性质与判定
“两直线平行,内错角相等”与“内错角相等,两直线平行”
角的平分线的性质与判定
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
解
已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE(角平分线上的点到角的两边的距离相等).
∴ OE是CD的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(1)写出命题“全等三角形的面积相等"的逆命题 .
(2)直角三角形的两个锐角互余的逆命题为 .
(3)命题"正方形是轴对称图形”的逆命题是 .
例2
交换原命题的题设和结论
面积相等的三角形全等
有两个角互余的三角形是直角三角形
轴对称图形是正方形
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,AB=8,则ΔABE的周长为 .
例3
解
[答案]18
[详解]解:∵DE是BC的垂直平分线,交AC于点E,
∴EB=EC,
∵点F是线段AC的中点, AC=2CF,
∵△ABE的周长是AB+BE+AE=AB+EC+AE
=AB+AC,CF=5,AB=8,
∴AB+BE+AE=AB+AC=8+2x5=18.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,AD⊥BC,BD = DC,点 C 在 AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
A
B
E
D
C
解:AB = AC = CE,AB + BD = DE.
理由:
∵AD⊥BC,BD = DC,
∴AD 是 BC 的垂直平分线.
∴AB = AC.
又点 C 在 AE 的垂直平分线上,
∴AC = CE.
∴AB = AC = CE.
又 BD = DC,
∴AB + BD = CE + DC,即 AB + BD = DE.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图, AB=AC, MB=MC. 直线AM 是线段BC 的垂直平分线吗 为什么
解:∵AB=AC,MB=MC,
∴直线AM是线段BC的垂直平分线,(到线段两端距离相等的点在这条线段的垂直平分线上)
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)两直线平行,同位角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
解:(1)同位角相等,两直线平行,为真命题
(2)如果两个实数的绝对值相等,那么它们也相等,为假命题
(3)如果两个三角形的对应角相等,那么它们为全等三角形,为假命题
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4. 如图,P 是 △ABC 内一点,若 PB = PC,则点 P 在( )
A.∠ABC 的平分线上
B.∠ACB 的平分线上
C.边 AB 的垂直平分线上
D.边 BC 的垂直平分线上
D
5.如图,在△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是 ( )
A.8 B.9 C.10 D.11
C
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6. 如图,公园里有一块三角形草坪(△ABC),现准备在该三角形草坪内种一棵树,使得该树到△ABC 三个顶点的距离相等,则该树应种在( )
A.三条边的垂直平分线的交点处
B.三条角平分线的交点处
C.三条高的交点处
D.三条中线的交点处
A
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·江苏连云港·中考真题)如图,在△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,则△AEG的周长为( )
A.5 B.6 C.7 D.8
[答案]C
[分析]本题考查了线段垂直平分线的性质,由线段垂直平分线的性质可得AE=BE,AG=CG,再由三角形的周长公式计算即可得解,熟练掌握线段垂直平分线的性质是解此题的关键,
[详解]解:∵DE垂直平分AB,GF垂直平分AC,
∴AE=BE,AG=CG,
∴△AEG的周长为AE+AG+EG=BE+CG+EG=BC=7,
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2025·四川达州·中考真题)如图,在△ABC中,AB=AC-8,BC=5,线段AB的垂直平分线交AB于点E,交AC于点D,则△BDC的周长为( )
A.21 B.14 C.13 D.9
[答案]C
[分析]本题主要考查了线段垂直平分线的性质,根据线段垂直平分线的性质可得AD=BD,据此根据三角形周长计算公式求解即可.
[详解]解:.线段AB的垂直平分线交AB于点E,交AC于点D,
∴AD=BD,
∴△BDC的周长=BD+BC+CD=BC+CD+AD=BC+AC=8+5=13,
故选: C.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
垂直平分线性质及判定定理
完成对垂直平分线性质及判定定理的逻辑推导
能区分原命题与逆命题
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA = PB,
∴点 P 在 AB 的垂直平分线上..
几何语言:
P
A
B
l
C
线段的垂直平分线可以看成与这条线
段两个端点距离相等的所有点的集合.
作用:判断一个点是否在线段的垂直平分线上.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 对比角的平分线与线段的垂直平分线
名称 角平分线 线段垂直平分线
图示
性质
判定
C
A
B
O
D
E
P
A
B
P
C
角平分线上的点到角两边的距离相等
线段垂直平分线上的点与这条线段两个端点的距离相等
角的内部到角两边距离相等的点在角的平分线上
与线段两个端点距离相等的点在这条线段的垂直平分线上
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
知识点 互逆命题与互逆定理
两个命题的题设、结论正好相反.
我们把具有这种关系的两个命题叫作互逆命题. 如果把其中一个叫作原命题,那么另一个叫作它的逆命题.
一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作互逆定理,其中一个定理叫作另一个定理的逆定理.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:4、6题.
B层:P69习题 15.1:5题.
下 课
同课章节目录
